海上风电结构过渡段灌浆体的疲劳性能研究*

张冬冬 程晔 王法武 朱词

1.江苏商贸职业学院建工学院 南通226011

2.南京航空航天大学土木与机场工程系江苏省机场基础设施安全工程研究中心 210016

引言

采用单桩基础的海上风电结构由于构造简单、加工制造及运输方便，适合大批量生产，因此得到了广泛的应用。对于单桩基础的海上风电结构而言，过渡段主要是指对桩基础与外套筒的环形空间灌浆后，形成的一个封闭整体部分［1］。过渡段作为海上风电结构的重要连接部分，其疲劳性能直接影响电力机的使用寿命。国外已经报道了多起海上风机由于过渡段灌浆体疲劳破坏的事故，故对其疲劳性能进行研究十分重要。针对风电其他部位结构的疲劳问题，国内外学者已经进行了比较深入的研究。李良碧等［2］以某2MW近海风机单桩式支撑结构为研究对象，采用谱疲劳分析法进行了疲劳分析，基于线性疲劳损伤累积理论和S-N曲线计算出结构总的疲劳损伤度和疲劳寿命。刘畅［3］以海上某风场的张力腿式风机支撑结构为研究对象，在风空气动力载荷和水动力荷载的联合作用下，根据S-N曲线和线性疲劳损伤累积理论，对风机支撑结构进行了疲劳寿命分析。于海鹏等［4］对波浪作用下大型海上风机的三桩式支撑结构进行了疲劳分析，根据Miner 线性损伤累计准则，计算支撑结构的疲劳损伤。目前，针对海上风电结构的疲劳研究主要关注于支撑结构。本文针对采用单桩基础的海上风电结构进行有限元数值模拟，结合Miner 疲劳分析理论，研究了在不同设计参数情况下过渡段灌浆体的疲劳性能。

1 灌浆体的疲劳分析理论

Palmgren-Miner理论在线性损伤累积理论中最为经典，又被简称为Miner 理论［5，6］，其累积损伤度D计算公式为：

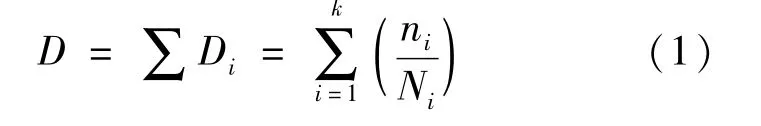
式中：Di为第i个应力水平的损伤度；ni为在第i个应力水平的循环数；Ni为由相应材料对应的常幅曲线得到的第i个应力水平单独作用到破坏的允许循环数；K 为分析中所考虑的应力水平数。

根据Miner理论来计算灌浆体长期应力循环的累积损坏，考虑海上风电结构的使用寿命为20年，相应的灌浆体使用寿命也为20 年。根据DNA规范［7］，分析灌浆体内不同范围的Tresca应力，计算其疲劳累积损伤度D时破坏允许的循环次数Ni如式（2）和式（3）［8］：

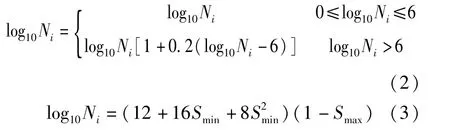
式中：Smin为最小相对应力，等于Smin，f／fcck，f；Smax为最大相对应力，等于Smax，f／fcck，f；Smin，f为灌浆体Tresca循环应力范围的最小值；Smax，f为灌浆体Tresca循环应力范围的最大值；fcck，f为灌浆体设计疲劳强度，等于fcck／rm＝130／2.6 ＝50MPa。fcck为灌浆体的特征柱体抗压强度，根据实际灌注材料取值130MPa；rm为材料抗力系数，在疲劳极限状态取2.6。

灌浆体应力变化范围可按式（4）［8］计算：

2 数值模型

2.1 风机结构模型

研究中选取的风机参数主要参考NREL（美国国家能源部可再生能源实验室）的主流5MW海上风机，如图1a所示，其各部分主要情况如下：（1）风机组、叶片、风轮。风轮方向及配置：上风向，3 叶片；控制方式：变速变桨；风轮及轮毂直径：126m，3m；轮毂高度：90m；切入、额定、切出风速：3m／s、11.4m／s、25m／s；额定叶尖速度：80m／s；叶片长度：61.5m；偏航速度：0.3°／s；机舱质量：230t；风轮质量：110t。（2）塔筒。塔筒高度：85m。

海上风电结构整体系统比较复杂，为提高计算效率，针对研究对象，将其有限元模型简化为由桩周土体、桩、灌浆体、外套筒、塔筒、顶部质量块共同组成，如图1b 所示。基准工况时，各部分的参数如下：桩体为钢管桩，其长度为90m，直径为6m，壁厚tp为0.06m，入土深度为60m，露出桩的长度HP为30m；灌浆体的长度Lg为9m，厚度tg为0.15m，外套筒壁厚ts为0.06m；塔筒为下大上小的钢制薄壁筒模型，高度ht为85m，底部厚度为0.06m，顶部厚度为0.027m，底部与钢管桩相衔接；风轮-机舱系统作为一个整体考虑，简化为一个环形质量块，底部与塔筒相衔接，质量mf为340t。为考虑桩与土体的相互作用，土体的水平范围取为桩径的10倍，厚度为70m，同时在土体四周和底部施加固定约束并设置无反射边界条件；根据分析需要，将模型各部分采用不同尺寸的网格划分后，参考文献［9］进行模态分析，计算其一阶自振频率为0.308Hz，符合5MW海上风机工程设计自振频率的范围。

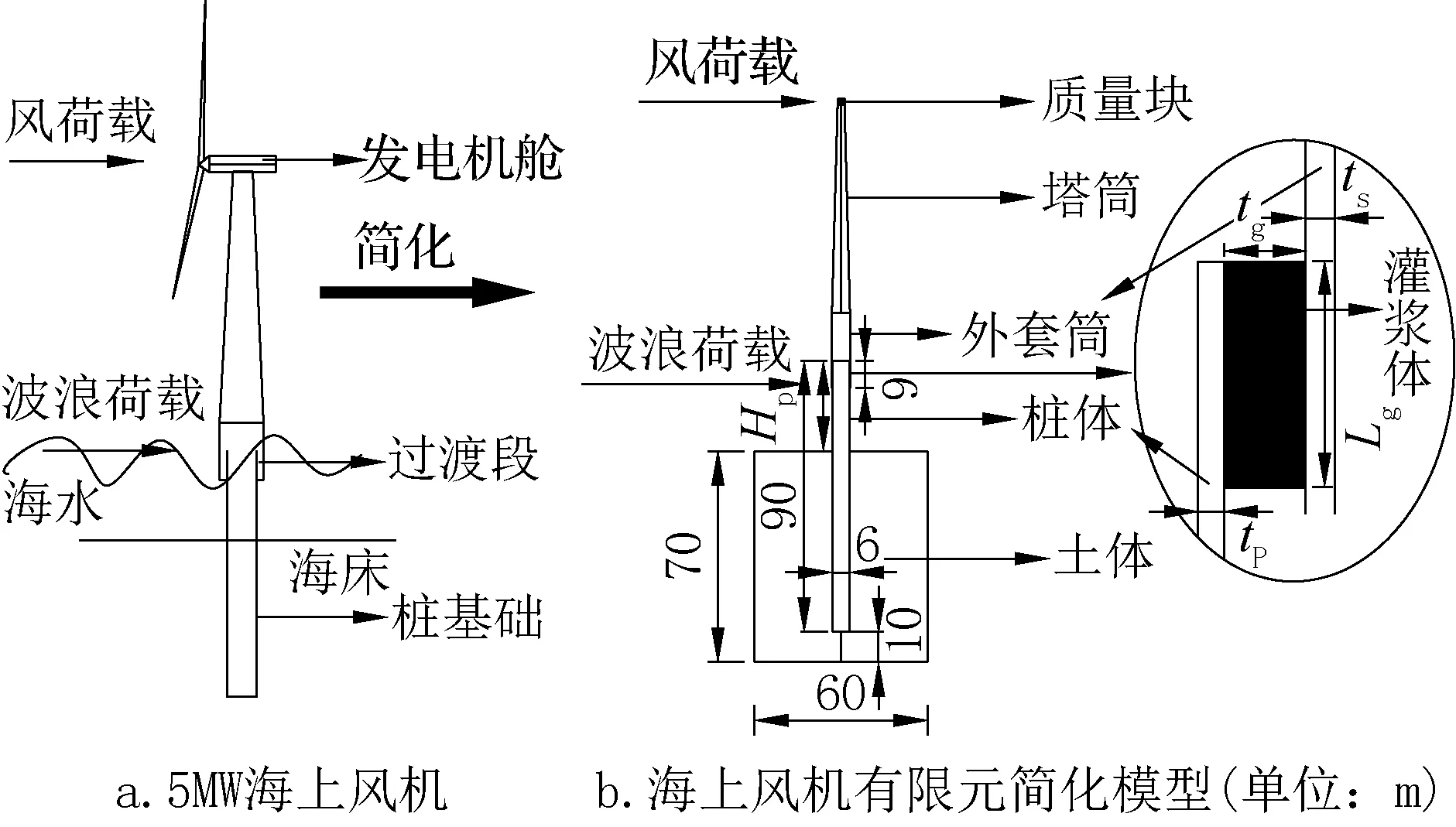
图1 海上风电结构简化模型Fig.1 Simplified model of offshore wind power structure

模型采用的单元类型均为实体单元SOLID45。桩、外套筒、塔筒和灌浆体的材料均采用Linear Isotropic模型，为各向同性线弹性材料模型，相应的参数设置如下：桩、外套筒和塔筒的密度ρ 为7850kg／m3，弹性模量E 为2.1 ×1011Pa，泊松比μ为0.3；灌浆体的密度ρ为2440kg／m3，弹性模量E 为5.5 ×1010Pa，泊松比μ 为0.19。桩与土体之间、灌浆体与桩体、灌浆体与和外套筒之间均设置为面面接触。桩周土体参考文献［10］设计采用Drucker-Prager（D-P）模型，相应的参数设置如下：密度ρ为1900kg／m3，剪切模量G为70MPa，泊松比μ为0.28，内摩擦角α为25°，粘聚力C为60kPa。

2.2 风荷载和波浪荷载

研究中风机所受的水平向风荷载采用GHBladed风机软件，基于叶素理论计算［11，12］。正常发电工况条件下，近海风电机组轮毂处平均风速取15m／s，塔筒顶部风机所受的水平向风荷载时程曲线，如图2 所示。风荷载水平施加在塔顶等效质量块中心处。

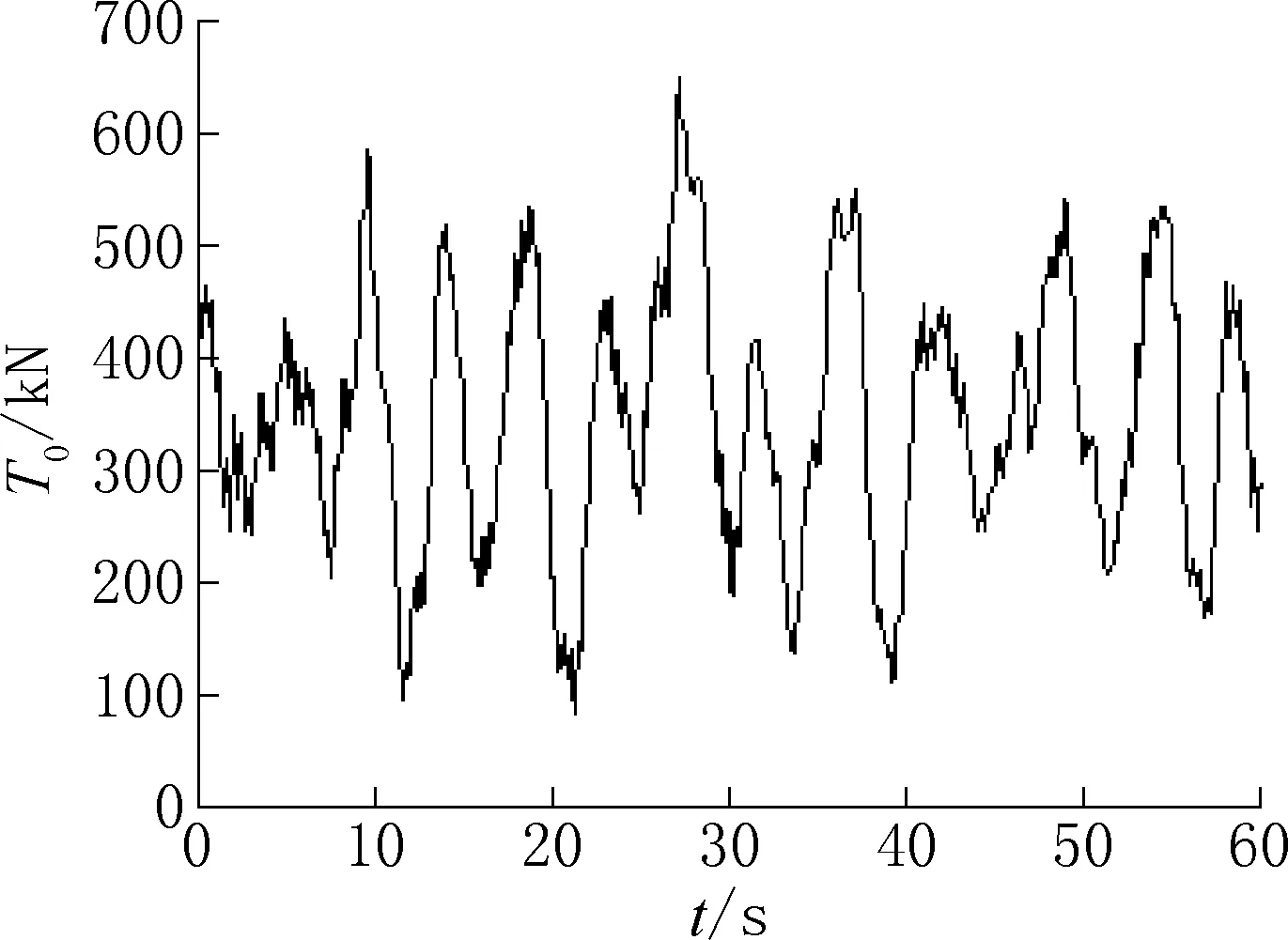
图2 风荷载的时程曲线Fig.2 Time history curve of wind load

采用Airy（线性）波理论来描述波浪运动，同时采用莫里森方程对规则波的荷载进行计算。根据我国海港水文规范和港口技术规范［13］，风电机组正常发电工况条件下，研究中近海区域波浪参数取值为：波高H ＝5.5m，波长L ＝75m，周期T1＝7.2s。将线性波上水质点速度和加速度代入莫里森方程中，沿波面对其进行积分，得到作用在桩上的波浪荷载，如图3 所示。波浪荷载水平向施加在距离地面30m的桩侧中轴线处。

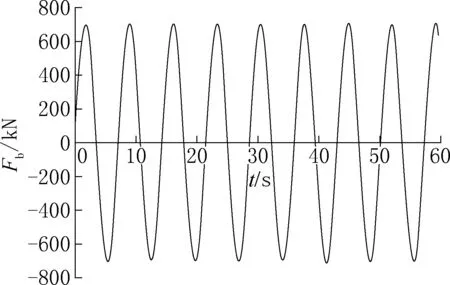
图3 波浪荷载的时程曲线Fig.3 Time history curve of wave load

研究中考虑风荷载与波浪荷载叠加影响，两者以同方向施加。

3 过渡段灌浆体的疲劳危险节点及损伤度

3.1 过渡段灌浆体的疲劳危险节点

根据DNV 规范［7］，对海上风电机组正常发电工况下，风电结构过渡段的疲劳性能进行分析，同时考虑风荷载和波浪荷载的作用方向一致。在塔顶和过渡段的同一方向上，对塔顶和过渡段外套筒同时施加水平静力，找出其疲劳危险节点所在的大致部位，即疲劳危险部位。

根据过渡段灌浆体节点的Tresca应力计算云图以及灌浆体、桩体和外套筒的对称性，灌浆体的疲劳危险部位共6 处，即上边缘部位荷载施加方向上2 处，下边缘部位荷载施加方向上2 处，以及荷载施加垂直方向一侧部位上、下边缘2 处。

在此基础上，将水平静力改为风荷载和波浪荷载，参考文献［14］的有限元计算方法进行动力时程分析。从上述得到的灌浆体的6 个危险部位中，每个危险部位分别找出了2 个Tresca 应力时程曲线峰值最大的节点，一个靠近桩体在内侧，一个靠近外套筒在外侧，共12 个节点，如图4所示。针对这12 个节点，进一步分析比较其Tresca应力时程曲线，确定灌浆体下边缘6 个节点中最为危险的2 个节点节点A下内左、节点B下内右，灌浆体上边缘6 个节点中最为危险的2个节点节点C上外左、节点D上内左（第一个下标表示灌浆体的上、下边缘，第二个下标表示节点所处的内、外部位，第三个下标表示荷载施加从左到右方向上的顺序）。

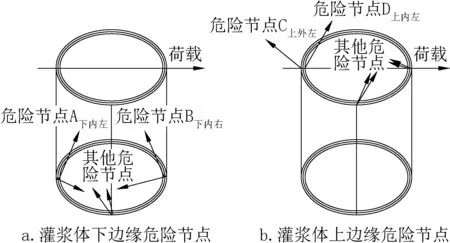
图4 灌浆体上、 下边缘处应力峰值最大的12 个节点Fig.4 12 nodes with the maximum stress peak at the upper and lower edges of grouting

灌浆体4 个最危险节点，即疲劳危险节点的应力时程曲线如图5 所示，此时灌浆体厚度为0.15m。

图5 灌浆体疲劳危险节点的Tresca 应力时程曲线Fig.5 Tresca stress time history curve of fatigue dangerous node of grouting

3.2 灌浆体疲劳危险节点损伤度计算

采用雨流计数法［15，16］处理疲劳危险节点的Tresca应力时程曲线，得到疲劳危险节点循环应力谱。提取出20 年内可用于疲劳危险节点损伤度计算的循环应力范围和循环次数ni。根据灌浆体疲劳累积损伤计算公式（2）、公式（3）求得相应循环应力范围的可循环次数Ni。利用Palmgren-Miner准则求得不同循环应力范围所造成的损伤度Di，最终累积得到灌浆体节点A下内左、节点B下内右、节点C上外左、节点D上内左的20 年应力谱累积损伤度D 分别为0.0572、0.0542、0.0441、0.0338，灌浆体下边缘的损伤度大于上边缘处。

4 不同结构设计参数对灌浆体疲劳性能的影响

首先考虑灌浆体自身特性，分析灌浆体的厚度tg、灌浆体的长度Lg变化对灌浆体疲劳性能的影响；然后，考虑灌浆体接触部分的结构特性，分析外套筒的壁厚ts、桩体的壁厚tp的影响；最后分析露出桩的长度Hp、塔筒的高度ht、风轮-机舱的质量mf以及土体的剪切模量G 等因素的影响。

4.1 灌浆体厚度tg 对灌浆体疲劳性能的影响

tg分别取为0.09m、0.12m、0.15m、0.18m、0.21m，其他参数不变，其疲劳危险节点20 年累积损伤度D 变化情况如图6 所示。随着tg的增加，D逐渐减小，并且下降的速度变慢，曲线斜率变小。tg从0.09m增加到0.21m，节点A下内左、B下内右、C上外左、D上内左的D 值分别下降了67.13%、65.62%、66.14%、67.86%。

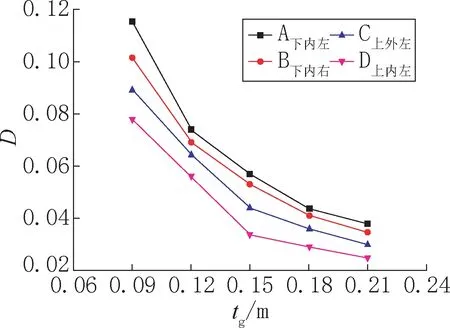
图6 厚度不同的灌浆体疲劳危险节点的累积损伤度Fig.6 The cumulative damage diagram of the joints with different thickness

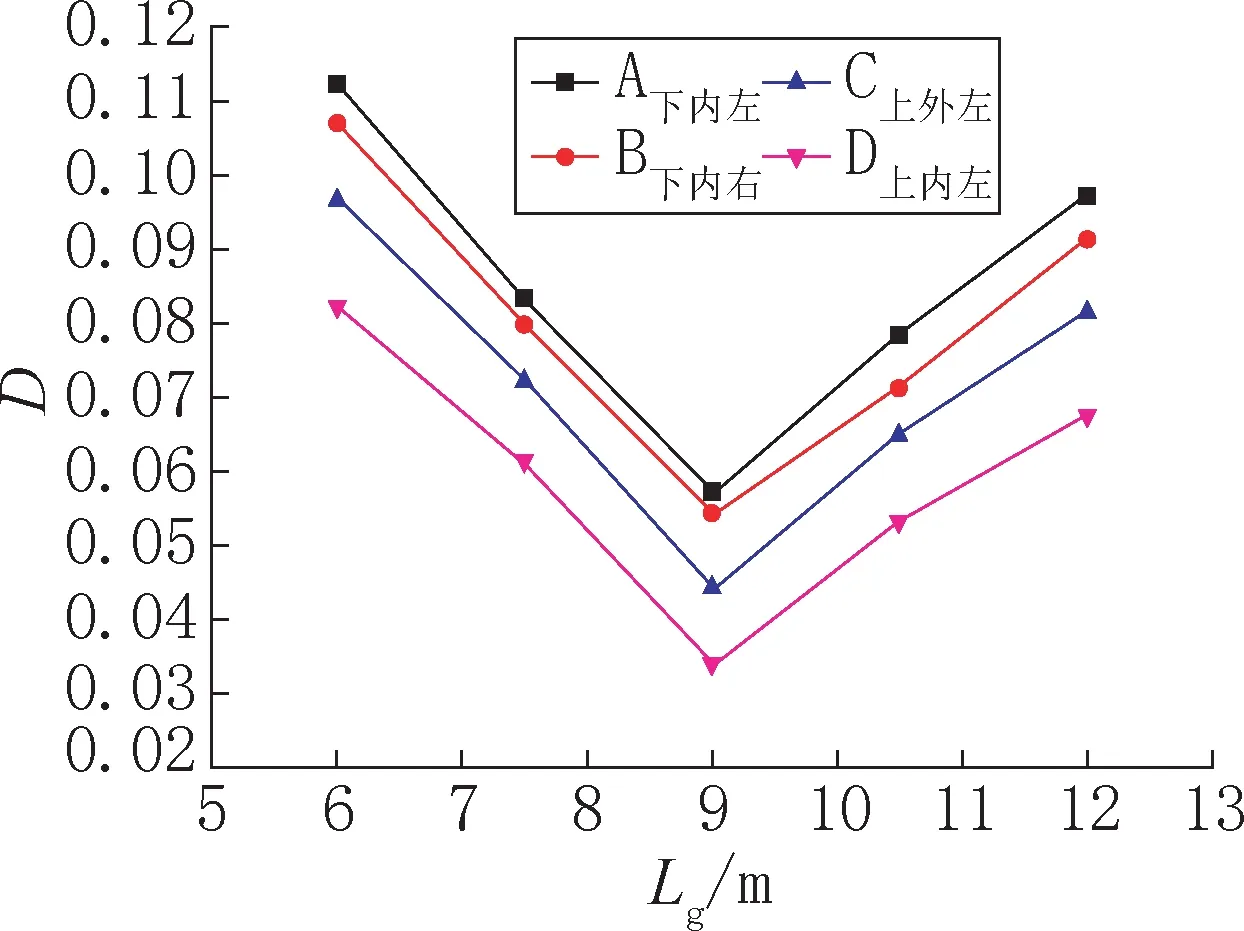
图7 长度不同的灌浆体疲劳危险节点的累积损伤度Fig.7 The cumulative damage diagram of the joints with different length of grouting

4.2 灌浆体的长度Lg 对灌浆体疲劳性能的影响

Lg分别取为6m、7.5m、9m、10.5m、12m，其他参数不变，其疲劳危险节点20 年累积损伤度D 变化情况如图7 所示。随着过渡段灌浆体长度Lg的增加，D 先下降后上升，并且下降的速度比上升的速度快，曲线斜率先大后小。当Lg从6m 增大到9m，节点A下内左、B下内右、C上外左、D上内左的D 值分别下降了49.07%、49.39%、54.63%、59.03%。当Lg从9m 增加到12m，节点A下内左、B下内右、C上外左、D上内左的D 值分别上升了69.76%、68.27%、84.35%、100.30%。这表明当Lg约为1.5 倍桩径时，灌浆体的损伤度D最小。灌浆体的长度适当，则过渡段的连接效果和传力性能最佳，灌浆体疲劳性能也最佳。

4.3 外套筒壁厚ts 对灌浆体疲劳性能的影响

ts分别取为0.04m、0.05m、0.06m、0.07m、0.08m，其他参数不变，其疲劳危险节点20 年累积损伤度D 变化情况如图8 所示。随着ts的增加，D逐渐增大，并且增大的速度变慢，曲线斜率变小。ts从0.04m增加到0.08m，节点A下内左、B下内右、C上外左、D上内左的D 值分别上升了35.13%、37.77%、43.63%、42.68%。ts的增加对D值的上升作用，在从0.04m增加到0.07m时较为明显，此后ts的增加对D值的影响作用减弱。

4.4 桩体的壁厚tp 对灌浆体疲劳性能的影响

tp分别取为0.04m、0.05m、0.06m、0.07m、0.08m，其他参数不变，其疲劳危险节点20 年累积损伤度D 变化情况如图9 所示，随着tp的增加，D逐渐减小，并且减小的速度变慢，曲线斜率变小。tp从0.04m增加到0.08m，节点A下内左、B下内右、C上外左、D上内左的D 值分别下降了41.94%、41.62%、43.91%、43.31%。tp的增加对D值的降低作用，在从0.04m增加到0.07m时较为明显，此后tp的增加对D 值的影响作用减弱。

4.5 露出桩长度Hp 对灌浆体疲劳性能的影响

Hp分别取为15m、20m、25m、30m、35m，其他参数不变，其疲劳危险节点20 年累积损伤度D变化情况如图10 所示，随着露出桩长度Hp的增加，D逐渐减小，并且减小的速度变慢，曲线斜率变小。Hp从15m 增加到35m，节点A下内左、B下内右、C上外左、D上内左的D值分别降低了54.92%、53.51%、59.26%、58.32%。

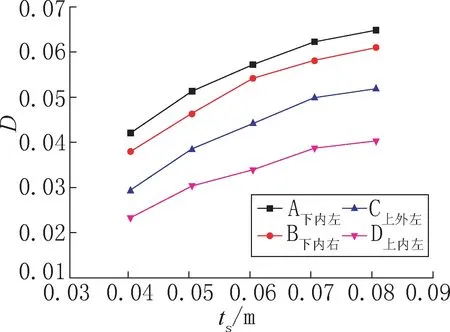
图8 外套筒壁厚不同的灌浆体疲劳危险节点的累积损伤度Fig.8 The cumulative damage diagram of the joints with different wall thickness of outer sleeve

图9 桩体壁厚不同的灌浆体疲劳危险节点的累积损伤度Fig.9 The cumulative damage diagram of the joints with different wall thickness of pile

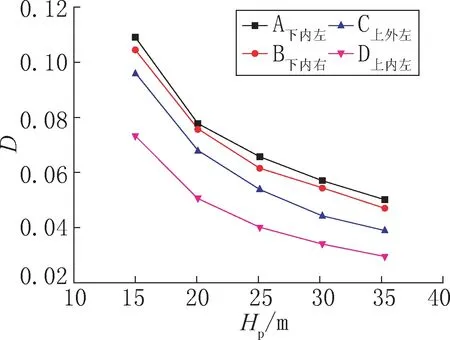
图10 露出桩长度不同的灌浆体疲劳危险节点的累积损伤度Fig.10 The cumulative damage diagram of the joints with different exposed pile length

4.6 塔筒高度ht 对灌浆体疲劳性能的影响

ht分别取为75m、80m、85m、90m、95m，其他参数不变，其疲劳危险节点20 年累积损伤度D变化情况如图11 所示，随着塔筒高度ht的增加，D逐渐增大，并且增大的速度变快，曲线斜率变大。ht从75m 增加到95m，节点A下内左、B下内右、C上外左、D上内左的D 值分别上升了290.34%、289.56%、304.78%、240.29%。随着ht的增大，对D 值增大影响越来越明显，尤其是ht大于85m之后。

4.7 风轮-机舱质量mf 对灌浆体疲劳性能的影响

mf分别取为300t、320t、340t、360t、380t，其他参数不变，其疲劳危险节点20 年累积损伤度D变化情况如图12 所示，随着风轮-机舱质量mf的增加，D 逐渐增大，并且增大的速度变快，曲线斜率变大。mf从300t 增加到380t，节点A下内左、B下内右、C上外左、D上内左的D值分别上升了530.43%、560.46%、553.33%、555.21%。随着mf的增大，对D 值增大影响越来越明显，尤其是mf大于340t之后。

4.8 土体剪切模量G对灌浆体疲劳性能的影响

G分别取为30MPa、50MPa、70MPa、90MPa、110MPa，其他参数不变，其疲劳危险节点20 年累积损伤度D 变化情况如图13 所示，随着土体剪切模量G的增大，D逐渐减小。G从30MPa增加到110MPa，节点A下内左、B下内右、C上外左、D上内左的D 值分别降低了53.45%、50.89%、54.46%、54.64%。

图11 塔筒高度不同的灌浆体疲劳危险节点的累积损伤度Fig.11 The cumulative damage diagram of the joints withdifferent tower height

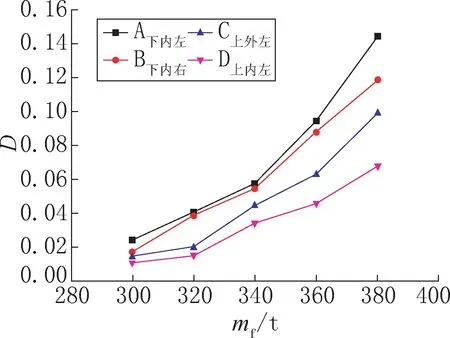
图12 风轮-机舱质量不同的灌浆体疲劳危险节点的累积损伤度Fig.12 The cumulative damage diagram of the joints with different quality of wind turbine and engine room

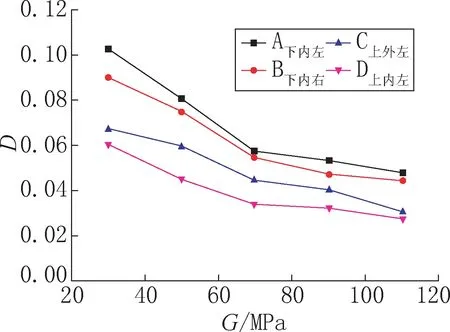
图13 土体剪切模量不同的灌浆体疲劳危险节点的累积损伤度Fig.13 The cumulative damage diagram of the joints with different shear modulus

同时，如图6 ～图13 所示，随着结构设计参数的改变，灌浆体下边缘节点A下内左、B下内右的D值始终比上边缘节点C上外左、D上内左大。结构设计参数ht、mf相较于其他设计参数，对灌浆体的损伤度D影响更大些。

5 结论

对采用单桩基础的5MW 海上风电结构进行有限元模型分析，结合雨流计数法及灌浆体疲劳累积损伤计算理论，进行疲劳累积损伤度计算，分析了不同的风电结构设计参数对过渡段灌浆体疲劳性能的影响规律，结论如下：

1.过渡段灌浆体下边缘的疲劳累积损伤度D比上边缘大。

2.当灌浆体的长度Lg约为1.5 倍桩径时，灌浆体的损伤度D最小。

3.随着过渡段灌浆体厚度tg的增加、外套筒壁厚ts的减小、桩体壁厚tp的增加、露出桩长HP的增加，塔筒的高度ht的减小、风轮-机舱的质量mf的减小、土体的剪切模量G 的增加，灌浆体的损伤度D逐渐减小。

4.当塔筒的高度ht、风轮-机舱的质量mf变化时，过渡段灌浆体在风荷载与波浪荷载组合作用下应力会产生较大变化，相较于其他设计参数对灌浆体的损伤度D影响更大些。