IFM系统的双交叠信号分析及改进*
王洪迅,王连河,王建,王士岩,王洪雷
(1.空军工程大学 航空工程学院,陕西 西安 710038;2.中国人民解放军93286部队,辽宁 沈阳 110141;3.中国人民解放军93149部队,甘肃 酒泉 735018)
0 引言
RWR(radar-warning receiver)/ESM(electronic warfare support measure)系统通过探测雷达信号,来识别载机所面临的威胁并进行告警,其中多以瞬时测频(instantaneous frequency measure,IFM)技术进行频率测试[1-3]。IFM瞬时带宽宽,动态范围大,分辨力高,测试速度快,可精测单个信号,但传统上认为对同时到达信号测频不正确。工程实践中一般设置同时到达信号检测电路,以标记测频错误[1-2]。文献[4]表明,若信号流超过500万脉冲数/s,IFM面临同时到达信号的概率超过10%(2个)和2%(3个)。由文献[4]可知,信号同时到达只是信号交叠的特例,IFM的信号交叠概率要远大于信号同时到达的概率。传统的IFM把交叠信号当作一个信号进行测频,这样的处理方式只能得到一个信号的频率,且存在一定的测频误差,误差的大小由2个信号的幅度、频率差等多种因素决定,因此传统上对交叠信号的处理方式极大地影响了IFM效能[4]。
诸多文献对IFM系统的交叠信号处理能力有深入分析。文献[5]提出一种对IFM交叠信号的处理方法,该方法在一定信噪比和两信号功率比的情况下,能够估计一个信号的频率,但无法估计交叠信号中另一个信号的频率。文献[6]虽然对瞬时测频的多值问题进行了分析,但提出的改进方案不能测量交叠信号频率。文献[7-9]基于傅里叶变换原理,对传统的IFM加以改进。其中文献[7-8]应用对短时傅里叶变换结果进行插值的方法,提高测频精度,可以准确地估计多个交叠信号的频率;文献[9]采用多结构的短时测频算法和基于线性调频Z变换(chirp Z transform,CZT)算法,缩短了测频时间,提高了测频精度。但这几种方法的瞬时带宽不够宽。文献[10]利用奇异谱分析(singular spectrum analysis,SSA)构建伪阵列信号,采用盲源分离算法(blind source separation,BSS)实现信号分离,但对频谱相近或重叠的交叠信号,此方法失效。文献[11]基于单比特接收算法,滑动快速傅里叶变换(fast Fourier transform,FFT)算法,提出了宽带单比特IFM接收技术,可估计交叠信号频率,具备大带宽、实时处理、高频率分辨率等优点,但这种算法的动态范围不够大,测频精度没有传统IFM测频精度高。
那么能否在保持IFM接收机原有优点的基础上,使其具备处理交叠信号的能力呢?本文通过分析交叠信号作用于IFM系统的工作机理,发现其具备这一能力。
1 IFM系统概述
典型IFM单元如图1所示[1],其基本组成为:功分器、延迟线、90°电桥、平方率检波器和差分放大器。

图1 实用微波鉴相器结构示意图
(1)
式中:K为检波器系数;A为信号幅度;φ为相角。
φ=2πfT,
(2)
式中:T为延迟线的时间延迟;f为输入信号的载频。
由式(1),(2)得,信号频率为
(3)
为了解决频段覆盖和分辨力的矛盾,工程上采用图2所示IFM并联结构[12],其主要有2种典型特征:
(1) 极性量化器+编码矫正结构。为了快速获取测量结果,通常采用极性量化器,由于各个支路测量结果有模糊,通过编码矫正逻辑,以获取正确的测量结果。
(2) 视频检波信号经整形,再经一定时间的延迟,形成锁存脉冲,从而获得信号的测量结果。
由于以上2个特征,使IFM对某一个具体的未知雷达脉冲信号只进行一次量化采样,输出为当前时刻的频率二进制码[1],因此这种传统的IFM系统对交叠信号测频时仅输出一个结果。大量实验证明,在双交叠信号的情况下,IFM系统可能输出信号1的频率码或信号2的频率码,也可能输出与信号1和信号2都无关的频率码[1]。下面从理论上分析IFM对交叠信号的处理情况。
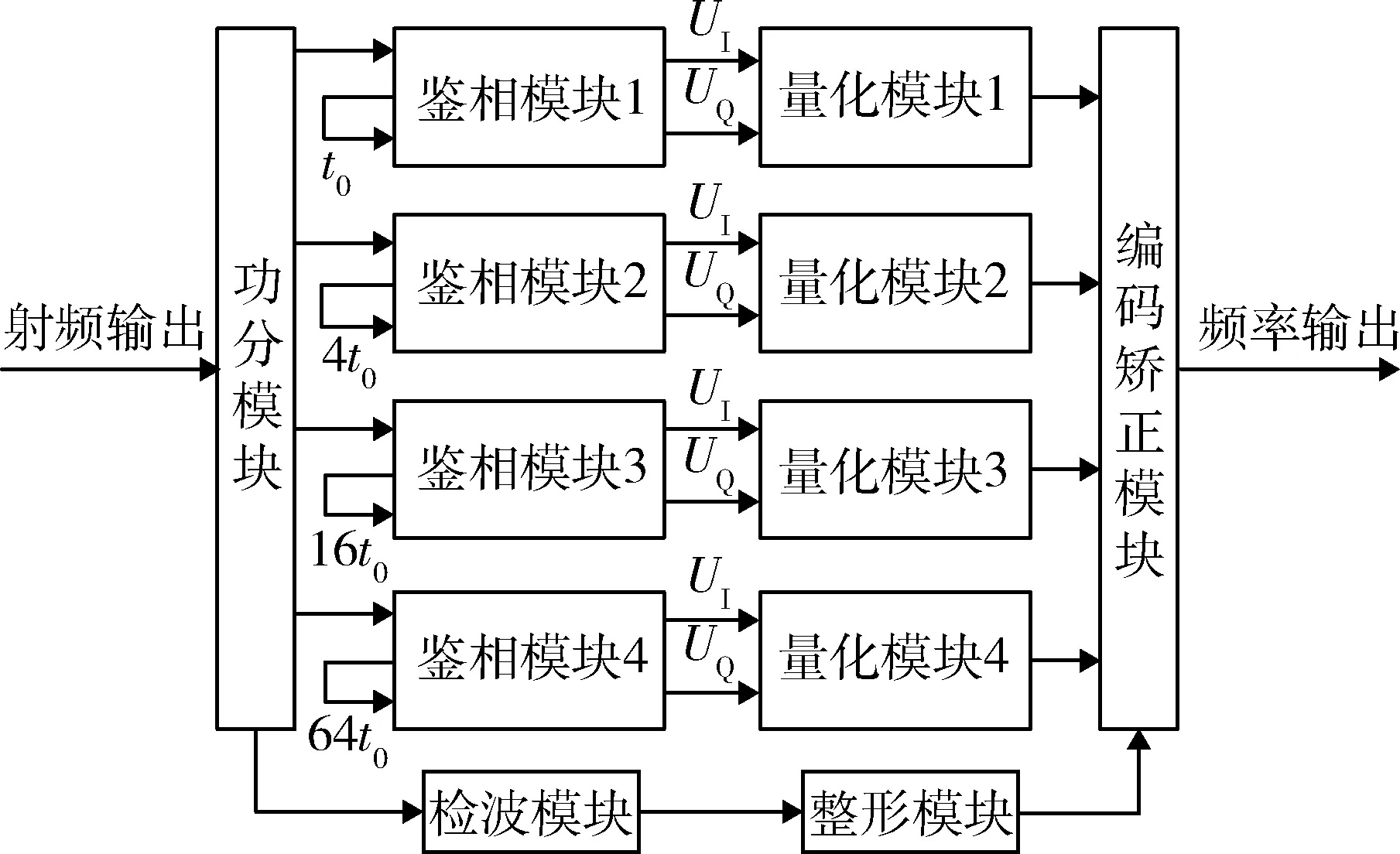
图2 传统IFM系统
2 交叠信号的IFM机理分析
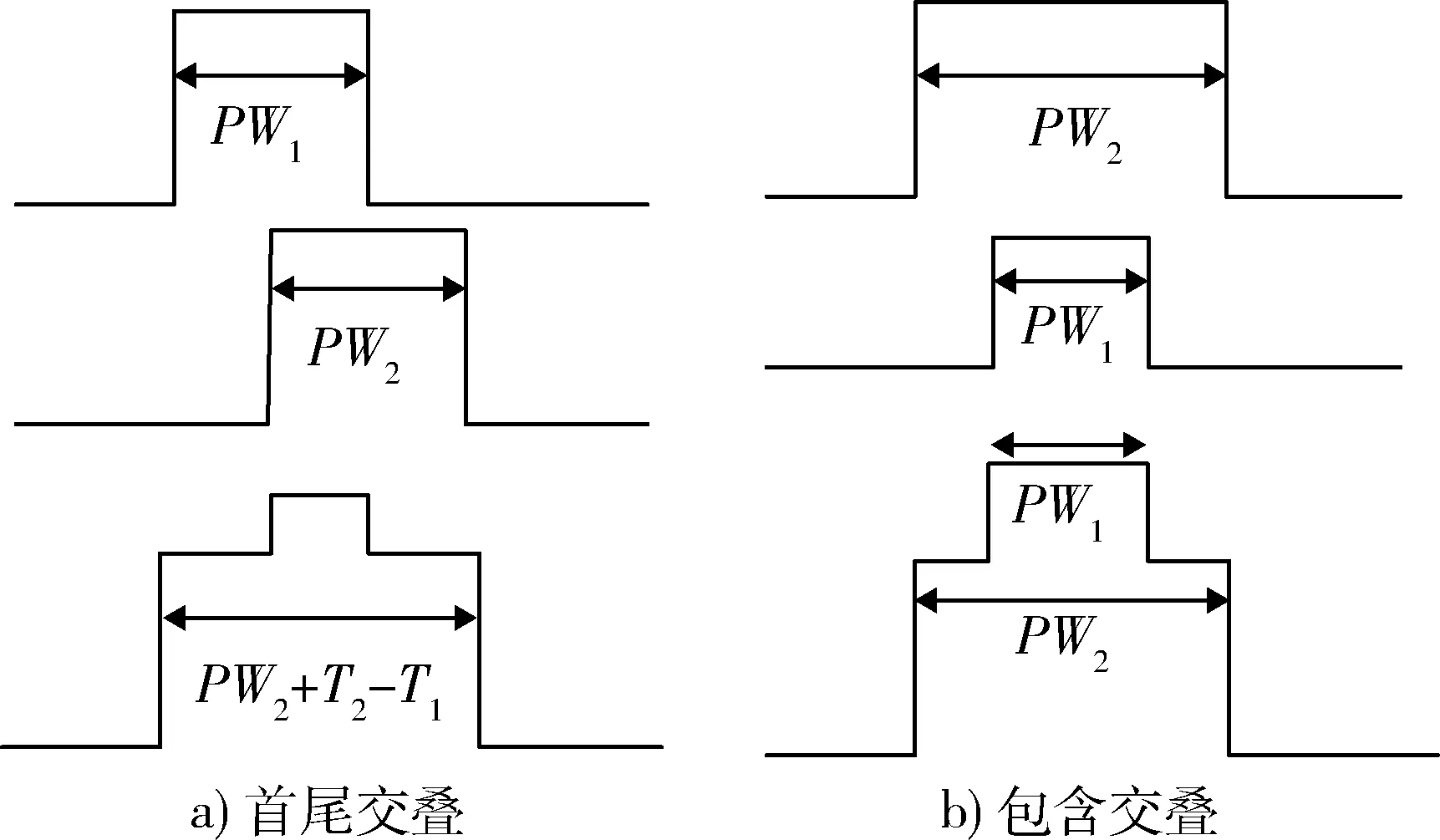
2.1 脉冲交叠简介
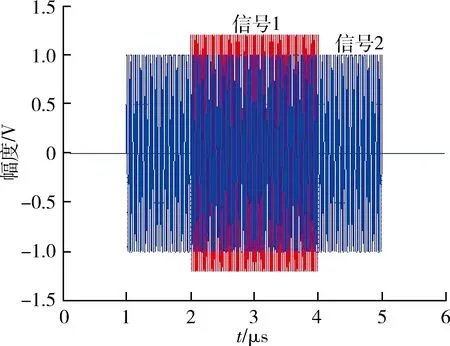
在复杂电磁环境下,由于IFM频带宽开,脉冲交叠不可避免。工程中2个脉冲完全交叠的概率是很小的[1],最基本的脉冲交叠是两脉冲首尾交叠和包含交叠[13]。根据文献[13],2个不同雷达脉冲到达时间分别为T1,T2,脉宽分别为PW1,PW2,当满足条件T1 出现多于2个脉冲交叠时,虽然情况较复杂,但基本都可视为脉冲首尾交叠和包含交叠的组合。由于2个以上脉冲交叠的概率较小[3],故此后续内容针对2个交叠信号作用于IFM系统进行分析。 对于图1所示微波鉴相器,若其输入端同时存在2个信号如式(4)所示。 图3 脉冲交叠图 (4) 则根据微波鉴相器工作原理,端口1信号可表示为公式(5);端口2信号可表示为公式(6);端口3信号可表示为公式(7);端口4,5信号可表示为公式(8);端口6,7信号表示为公式(9);端口8,9,10,11信号可表示为公式(10);端口8,9,10,11经过检波器和差分放大器后,如2ω1,2ω2,ω1+ω2的高频信号项被消掉,只剩直流和频率为ω1-ω2的差频信号,则端口UI(t)可表示为公式(11);端口UQ(t)可表示为公式(12);公式(11),(12)不便于分析,对其做合理的公式代换,如公式(13)所示。 (5) U2(t)=A1cosω1t+A2cos(ω2t+φ), (6) U3(t)=A1cos(ω1t-φ1)+A2cos(ω2t+φ-φ2), (7) (8) (9) (10) UI(t)=K{[U9(t)]2-[U8(t)]2}= 4A1A2cos[(φ1+φ2)/2]cos[(ω1- ω2)t-(φ1-φ2+2φ)/2], (11) UQ(t)=K{[U11(t)]2-[U10(t)]2}= 4A1A2sin[(φ1-φ2+2φ)/2]· cos[(ω1-ω2)t-(φ1+φ2)/2], (12) (13) 式中:A1,A2分别为2个信号的幅度;ω1,ω2为2个信号的角频率;φ为第2个信号的初始相位;φ1,φ2为2个信号经过延迟线所产生的相移,φ1=ω1Δl/Cg1=2πf1T1,φ2=ω2Δl/Cg2=2πf2T2;Δl为延迟线长度;Cg1,Cg2为延迟线中两信号的传播速度,工程中可近似相等。AI=4cos[(φ1+φ2)/2];AQ=4sin[(φ1-φ2+2φ)/2];φI=(φ1-φ2+2φ)/2,φQ=(φ1+φ2)/2。 需要指出的是公式(13)需要修正,这是由于差分放大器带宽的限制。设差分放大器的带宽为BWd,2个信号的频差为ω1-ω2=Δω。当Δω>>BWd时,差频分量全部被差分放大器滤除;当Δω< (14) 工程实际中,BWd一般为几十到几百兆赫兹[14],而为了防止临频干扰,通常2个雷达信号的频差Δω≫BWd。在这种情况下,差频分量被滤除,公式(14)修正为 (15) 对于图3a)所示首尾交叠的情况,微波鉴相器的I,Q输出值分为3个阶段: 当T1 (16) 当T2 (17) 当T1+PW1 (18) 对于图3b)所示脉冲包含的情况,微波鉴相器的I,Q输出值为:当T2 由文献[15]可知,可利用脉冲交叠部分的前后沿信息分离交叠信号。因此对于首尾交叠情况,根据T1 (19) 再由公式(3)估计信号1和信号2的频率。 由以上分析可知,无论是脉冲首尾交叠,还是脉冲包含交叠,只要得到一个信号的UI,UQ,均可通过两信号交叠区域的UI-12,UQ-12推算出另一个信号的UI,UQ,从而估计出2个交叠信号的频率。但传统的IFM接收机对一个脉冲信号只进行一次采样,无法进行UI,UQ的推算,因此需作连续采样。 综上所述,UI,UQ推算法可归结如下: (1) 用ADC(analog-to-digital converfer)模块对4路微波鉴相器的输出UI,UQ进行连续采样,得到离散电压值。 (2) 根据检波模块、整形模块输出确定2个脉冲的交叠区和非交叠区。 (3) 计算模块对交叠区和非交叠区的离散电压取平均,应用公式(3),(19)得2个信号的模糊频率值。 (4) 计算模块对4路输出的频率值作解模糊处理,得2个交叠信号的频率估计值。 上述算法的第3和第4步在图4框图的数字解算中进行。 图4 UI,UQ推算法框图 首尾交叠情况下,交叠前沿和后沿分别包含2个信号的频率信息,可直接获得,这里只仿真脉冲包含交叠的情况。 设IFM系统4路微波鉴相器延迟时间分别为0.15,0.6,2.4,9.6 ns,则频率覆盖范围可达到2~6 GHz;差分放大器带宽为10 MHz。对4路并行微波鉴相器的各个部件进行仿真建模,为模拟实际情况,在仿真中对输出加入信噪比为10 dB的噪声。给输入端馈入2个射频脉冲信号,这2个信号幅度分别为A1=1.2 V,A2=1 V;频率f1=4 000 MHz,f2=3 000 MHz;脉冲宽度τ1=2 μs,τ2=4 μs。在其输入端信号交叠情况如图5所示。此信号经过4路微波鉴相器后,若未考虑放大器带宽BWd的情况下,可得如图6所示4组UI,UQ值。 图5 2个交叠信号 图6 未考虑放大器带宽的UI,UQ值 其中2~4 μs的交叠部分与公式(14)的分析比较吻合。考虑BWd之后,差分放大器将4组UI,UQ的差频分量滤除,如图7所示。再用ADC对其输出的4组UI,UQ进行连续量化采样(设采样频率为16.7 MHz;量化间隔为0.187 5 V),所得100个离散电压值如图8所示。 图7 滤波后的UI,UQ值 图8 采样量化后的UI,UQ值 由以上仿真可知,改进后的IFM系统可以估计出2个交叠信号的频率,但测频精度受2个信号幅度的限制,为此作如下仿真: 表1 2个交叠信号的频率值 设2个信号的幅度比K12=A1/A2,信号2的幅度不变A2=1 V,信号1的幅度从0 V变化至 1.5 V,每次增加0.01 V。根据蒙特卡罗定理进行100次仿真,可得信号1的频率均方误差与2个信号幅度比的关系,如图9所示。由图9可知,2个信号的幅度比大于0.5时,信号1的测频误差小于3 MHz;幅度比大于1时,信号1的测频误差小于1 MHz。即信号幅度比大于0.5时可达到IFM精度要求。 图9 误差和幅度比的关系 由公式(14)可知,改进后IFM系统的测频精度受两信号频差和差分放大器的影响。设信号1的频率f1由3 001 MHz增至3 020 MHz,每次增加0.1 MHz;信号2频率f2=3 000 MHz,差分放大器带宽BWd=10 MHz。仿真100次,可得信号1的频率均方误差与两信号频差的关系,如图10所示。 图10 误差和频差的关系 由图10可知,当两信号的频差远大于10 MHz时,公式(14)中的差频分量被差分放大器滤除,此时测频精确,信号1的频率误差小于2 MHz;当两信号的频差在10 MHz左右时,公式(14)中的差频分量部分通过差分放大器,此时交叠部分的差频分量严重失真,信号1的测频误差很大;当两信号的频差远小于10 MHz时,公式(14)中的差频分量全部通过差分放大器。由于对UI,UQ采样值作时间平均处理,因此当差频分量是一个完整周期或一个完整周期倍数的信号时,差频分量被消除,此时测频精确。其他情况下存在差频分量,测频误差大。由此可知,当两信号频差大于差放大器带宽时,新算法可精确地估计2个交叠信号的频率。 由仿真验证和结果分析可得出如下结论: (1) 应用UI,UQ推算法能够估计双交叠信号的频率。 (2) 当2个信号的幅度比相差不大时,新算法具有较好的测频精度。 (3) 由于差分放大器的带宽不是很宽,所以新算法可处理在频域上接近的交叠信号。 (4) 新算法没有改变IFM的机理,因此依然具有瞬时带宽宽、动态范围大的特点。 (5) 新算法在一个脉宽内只采样100个数据,计算量小,运算简单,因此具有较好的实时性。 本文推导了两交叠信号经过IFM系统后的理论输出,建立了相应的数学模型,并提出了一种估计交叠信号频率的新算法—UI,UQ推算法,通过仿真验证了算法的有效性。本文的研究为今后IFM接收机的研制和改进提供了一种新的思路,工程中便于实现,有较好的实际应用价值。若未来的IFM接收机能够处理交叠信号,将大大提升其在复杂电磁环境下的适应能力。2.2 IFM脉冲交叠的理论分析
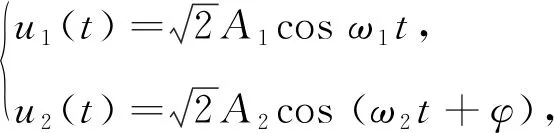

3 交叠信号频率估计
3.1 交叠脉冲的I,Q通道输出分析
3.2 UI,UQ推算法估计交叠信号的频率

4 仿真校验及分析
4.1 微波鉴相器I,Q通道输出仿真

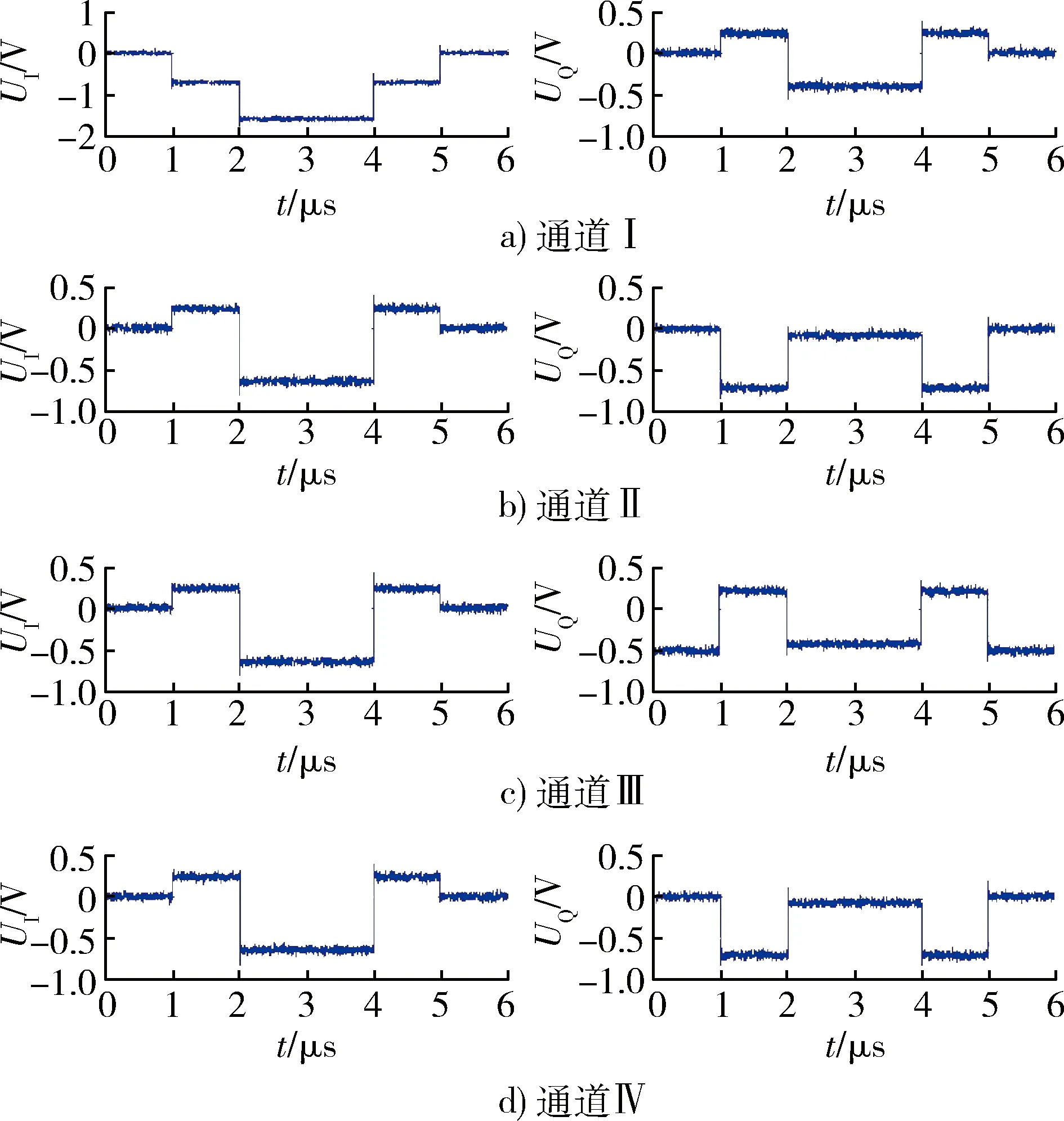
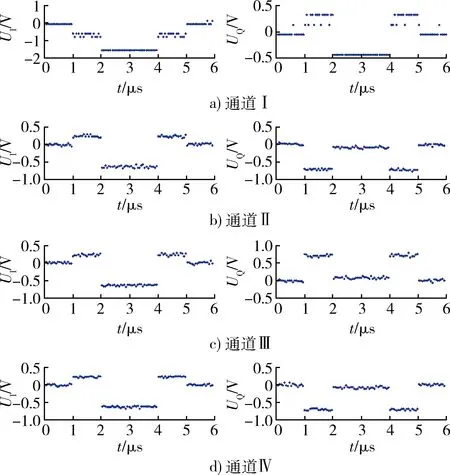
4.2 修正模糊、估计交叠信号频率

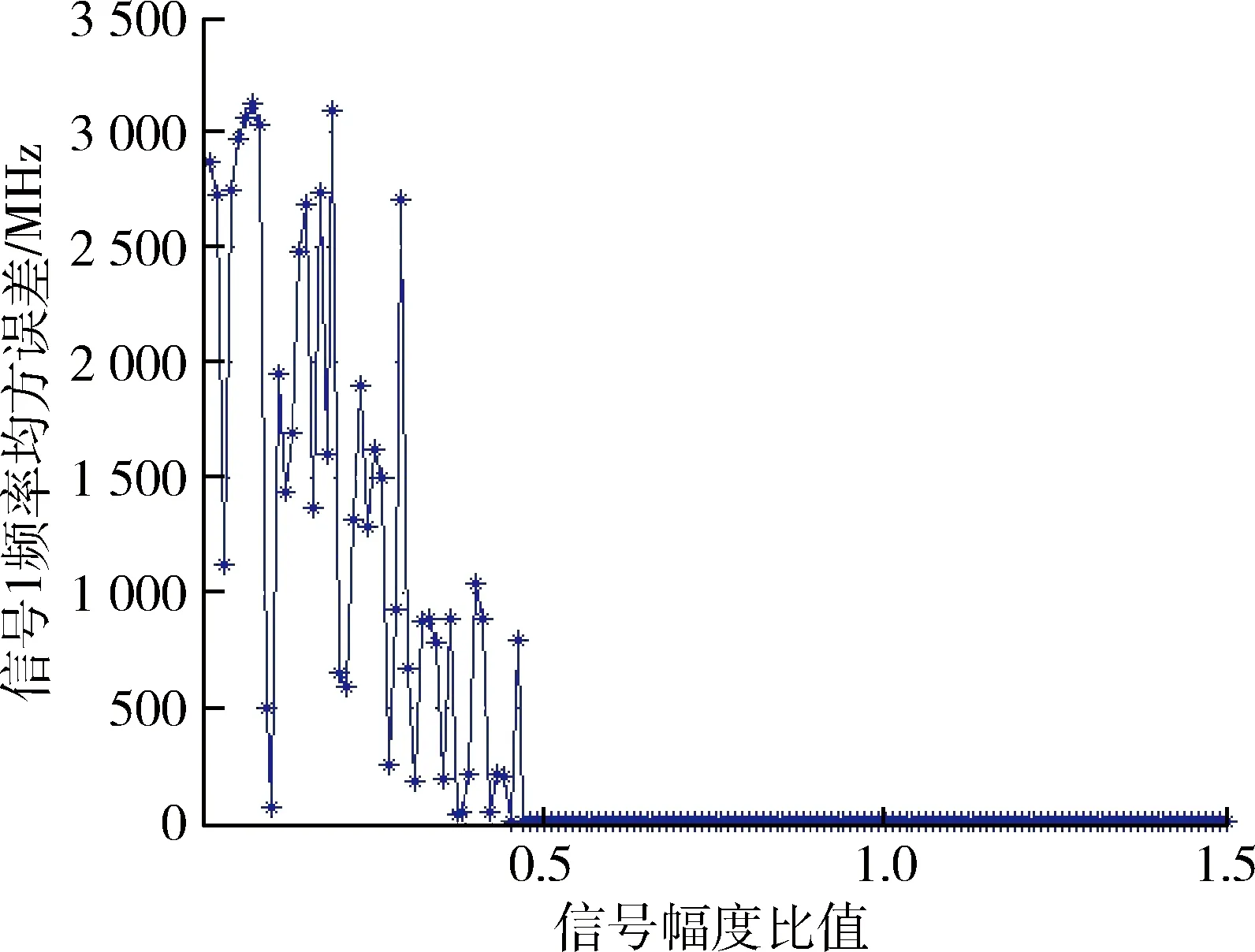
4.3 交叠信号幅度对测频精度的影响

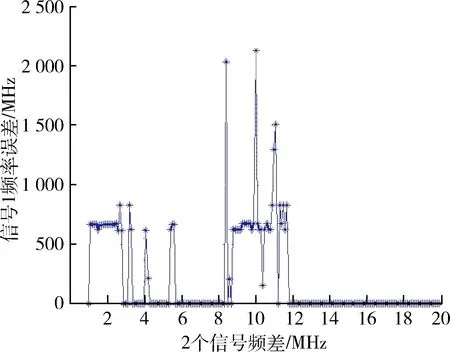
4.4 交叠信号频率差对测频精度的影响
4.5 仿真结论
5 结束语

