递进型优化算法对相控阵天线阵列的波束优化*
马小梦,何岷,张长革
(北京遥感设备研究所,北京 100854)
0 引言
相控阵雷达相比于传统的机械扫描雷达,利用电扫的方式对检测目标进行波束扫描,机敏灵活。电扫和多通道特征使相控阵天线在同一时间可实现多波束切换和多角度扫描,波束具有较高的增益,可实现多目标检测和跟踪[1]。电扫和多通道特性为相控阵天线阵列带来巨大优势的同时也带来了更多的误差和干扰,提升相控阵天线阵列波束性能是其广泛应用的前提,为此产生了权值校准、近远场检测等技术和方法[2-4]。
有源相控阵天线阵列含有多个子阵,各个子阵的天线幅度和相位分别由通道内的放大器、衰减器和移相器控制。这些器件由电控方式控制大小,受到芯片位数的影响,幅度和相位的实际值和设定值就产生了量化误差[5]。有源相控阵天线阵列的单元可以视作一个个矢量因子,阵列在空间中某点的电场强度可以视作各天线单元的波束矢量叠加和,而矢量因子的方向由移相器进行控制,这就是旋转电场矢量法对相控阵天线阵列的检测原理[6]。改进的旋转电场矢量法将检测角度放在子阵功率和上,这明显增加了检测误差,但对于大型有源相控阵天线阵列来说提升了检测效率[7]。在旋转电场矢量法基础之上,相位单元有源电场测量方法通过改变相位间隔检测出不同相位对应的功率和解算出天线单元电场分布,与理想电场对比得到补偿值[8]。功率测量法为优化开辟了途径,对移相器的量化误差理想化并建立移相器误差模型对阵列进行优化[9]。为了对移相器进行更加精确控制,建立编码系数矩阵与相移测量法结合实现对阵列的补偿,提高了检测精度[10-11]。
上述论文主要针对移相器产生的相位误差,在相控阵天线阵列中存在着天线单元间的耦合效应和边缘效应,两者对各天线单元的波束幅度和相位都产生干扰,对阵列波束的性能产生一定的影响[12]。基于压缩感知的方法将天线互耦效应、边缘效应和其他寄生效应考虑进来,独立测量各阵列单元实际的嵌入方向图,从接收信号中提取用于校准的角相关误差系数[13]。在针对边缘效应和互耦合的校准方法中允许扫描和加权所导致的不匹配产生的方向图退化,利用仿真软件将这些不良因素综合仿真,通过实测解算出阵列波束相关参数[14]。最小二乘法以优化天线方向图各项参数为目标,利用最小二乘法对子阵权值进行调校使得阵列波束各项参数不断优化,同时解决了相控阵天线快速测量和校准的问题[15-16]。
本文采用递进型算法对相控阵天线阵列波束进行改善,针对相控阵天线阵列中存在的量化误差、互耦和边缘效应等各项误差因子,通过对子阵的权值调校实现对波束优化,同时该方法灵活高效,可实现按设定的波束参数进行优化,递进方式使阵列得到更好的优化。
1 相控阵天线阵列的误差及干扰
相控阵导引头具有复杂的架构,从波形的产生到天线的射频发射,整个过程中存在着移相误差和天线阵列内的耦合等干扰。这些误差和干扰的存在使得相控阵天线阵列的波束产生波束展宽、增益下降等不良影响。为了简化分析,直接分析误差和干扰对天线单元波形的幅度和相位影响因子。
有源相控阵天线主要由功率放大器、移相器和发射天线组成,三者组成了发射机的各个通道,每一通道都可以通过改变衰减器和移相器的值调节发射天线的幅度和相位值,在设定天线阵列的指向后就可以设定每一通道的幅度和相位大小。由于数字控制的离散性,在设定相位值时存在着量化误差:
(1)
式中:φi为第i个通道中相位值;N为数字移相器的位数;n设定为与φi最接近的值。由于量化误差的存在,相位误差不可避免。
在相控阵天线阵列中,由于射频天线间距较小,天线单元间存在着电磁干扰。如图1所示。
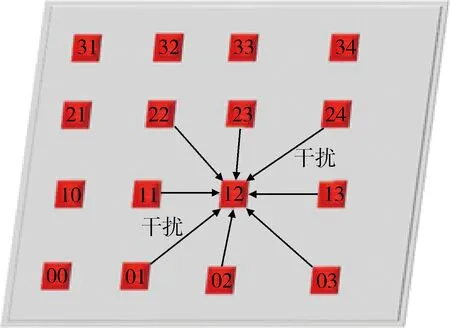
图1 射频天线干扰现象
天线单元12受到了周围各个天线单元的电磁干扰,距离越近,影响程度越深。最终使得射频天线单元的幅度和相位都产生漂移,影响波束合成的性能。如波束展宽、旁瓣抬高和零深减小,对于雷达系统性能而言会降低测角精度、跟踪精度。
考虑系统的误差和干扰的存在,最终阵列产生的波束为
(2)
式中:Ai为第i个天线单元的幅度;σi,σφi为幅度量化误差和相位量化误差;δi,δφi为幅度和相位的干扰因子;φi为阵列指向角度下的相位值。
公式(2)将相控阵天线阵列中的误差和干扰因子综合考虑进天线方向图中,为波束的优化提供了理论支撑。下面将引入权值校准方案和在此基础上的遗传算法,对天线方向图不断优化,从而达到减小阵列误差和抑制天线波束干扰的目的。
2 算法设计
2.1 子阵级权值校准
相控阵天线阵列误差及干扰无法避免,无论移相器和衰减器所输入的值是多少,产生的天线波束与理想波束存在着一定的误差。考虑到误差的不可避免,为了尽量减小误差所带来的影响,可以通过不断优化移相器和衰减器的参数来实现,这就是权值校准方法,也是工程实践中最常用的处理方法。
由于相控阵天线阵列在制作完成之后天线单元的发射波形幅度和相位不能改变,而通道由数字控制,可以通过通道对波束的幅度和相位进行控制。相比于阵元级权值校准,子阵级权值校准操控灵活,易于修改。阵元参数转换到子阵级参数需要子阵转换矩阵,该矩阵中包含幅度、相位和子阵形成矩阵。
TN×L=Φn(θ0)·W·T0,
(3)
式中:天线阵列为N行L列,它的子阵形成矩阵为T0;参数Φn(θ0)和W分别为各个阵元的相位和幅度构成的矩阵。为了实现对各个天线单元的权值校准,实现波束性能的提升,在阵元上加权贝叶斯权值。由于射频天线单元权值不可控,通过子阵形成矩阵就可以转换到子阵通道的权值大小。
wb=T0w,
(4)
式中:权值wb为贝叶斯权值矩阵,式(4)可实现阵元权值转换为子阵权值矩阵。通过子阵通道的功率放大器就可以实现子阵级权值的设定,实现幅度加权。在权值选择上,使用计算等旁瓣电平差波束的算法,该算法可应用在平面阵列,可以产生相等波束,同时可调整波束,使所有旁瓣低于所需水平。
图2中w为子阵级权值矩阵,wb1,wb2等为阵元级贝叶斯权值。通过式(3)可以实现阵元级权值向子阵级权值的转换。

图2 子阵加权模型
在此权值优化的基础上实现了阵列差波束的优化,得到较为理想的波束旁瓣电平。下面以权值优化算法为基础引入改进的遗传算法,将获得的权值矩阵进一步优化,使得阵列波束按照设定的波束宽度、旁瓣电平和零深等参数方向优化,实现对阵列误差和干扰的最大抑制。
2.2 改进的遗传算法
在常规的遗传算法(genetic algorithm,GA)中,目前都使用一种适应度函数fp或fw对空间进行优化。当适应度函数参数较少时运算效率高,收敛速度快;当参数较多时增加了适应度函数的约束条件,使得稳定性差并容易进入局部最优。为了抑制算法的缺点,本文引入两级适应度函数,避免算法进入局部最优,同时兼顾优化目标,使算法按照设定的参数标准得到优化。
经过2.1中权值分析,调整的对象为子阵级权向量w,但最终的优化目标是抑制天线阵列互耦对天线方向图的旁瓣电平、波束宽度和零深影响。这里将设定两级适应度函数:
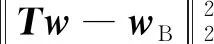
(5)
(6)
式中:wB为贝叶斯权值向量;
ΔSLL=SLL-SLLep,ΔBW=BW-BWep,ΔND=ND-Nep,
分别为天线方向图旁瓣电平、主瓣宽度、零深的优化值和期望值之差;kSLL,kBW,kND分别为它们的权重,三者满足kSLL+kBW+kND=1.
通过适应度函数fw可以得到逼近贝叶斯权值的子阵加权值,获得等旁瓣差波束天线方向图。在优化子阵权值的基础上,适应度函数fp综合考虑了阵列波束的波束宽度、旁瓣电平和零深,使得波束按照设定的优化目标进行优化。
第1步通过fw进行遗传优化至最优解,从中选出一定数量的子阵级权值向量,这些被选出的向量逼近最优解。第2步以这些选拔出来的优化向量组成新的种群,以fp为适应度函数,再遗传一定代数后退出。贝叶斯权值逼近为第2步的遗传优化提供了初始种群,减小了计算量,极大地提高了运算效率。
算法实现分2步完成,流程如图3,4所示。

图3 权值优化流程图
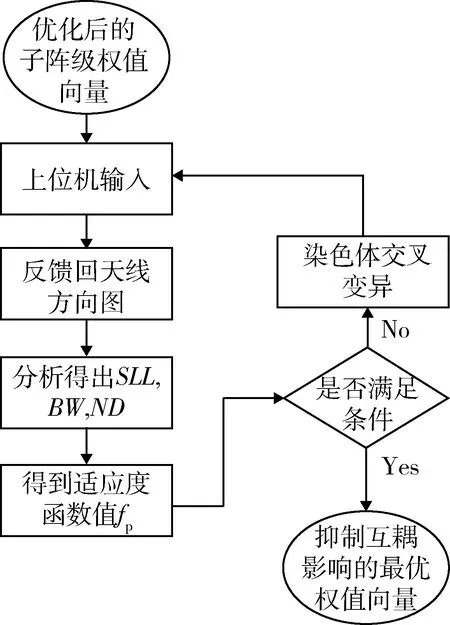
图4 遗传算法流程图
图3,4给出了详细的优化流程,下面将通过仿真实现递进型算法。分别对贝叶斯权值进行拟合以及波束参数的不断优化,实现对阵列误差及干扰的最大抑制。在对波束参数的优化中,需要不断反馈阵列天线方向图并提取参数,同时进行权值改进达到最终设定的优化参数目标。
3 实验仿真及结果分析
在分步优化过程中,第1步运算量较小,需要在庞大的种群中遗传迭代出适合进一步优化的小种群,优化的标准是与贝叶斯权值曲线的拟合。经过2 000代的遗传优化,最终拟合出理想的的子阵级权值曲线,如图5所示。
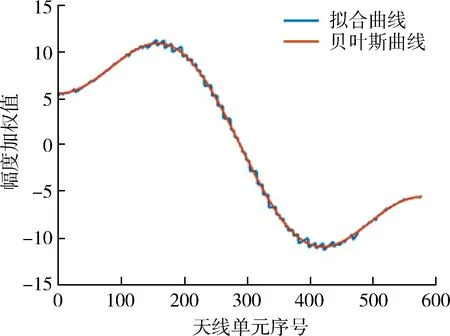
图5 贝叶斯权值拟合效果图
经过优化后的权值向量分布在Bayliss权值曲线的附近,优化效果明显。图6显示了适应度值的变化过程,达到了收敛的目的。
可以看出,在遗传迭代1 000次左右就有了收敛的效果。下面对优化的天线方向图提取相应参数,不断优化权值向量,使天线方向图参数向着设定的值不断逼近。逼近的效果反映在适应度函数值上,图7显示了这一变化过程。
适应度值fp不断减小,表明天线方向图向设定的参数值不断逼近,修改的权值向量对干扰和误差的影响不断抑制,最终实现了优化的目的。权值优化的效果主要体现在天线方向图的旁瓣电平、零深和主瓣宽度上,将这3个参数标注在仿真的天线方向图中,如图8~10所示。
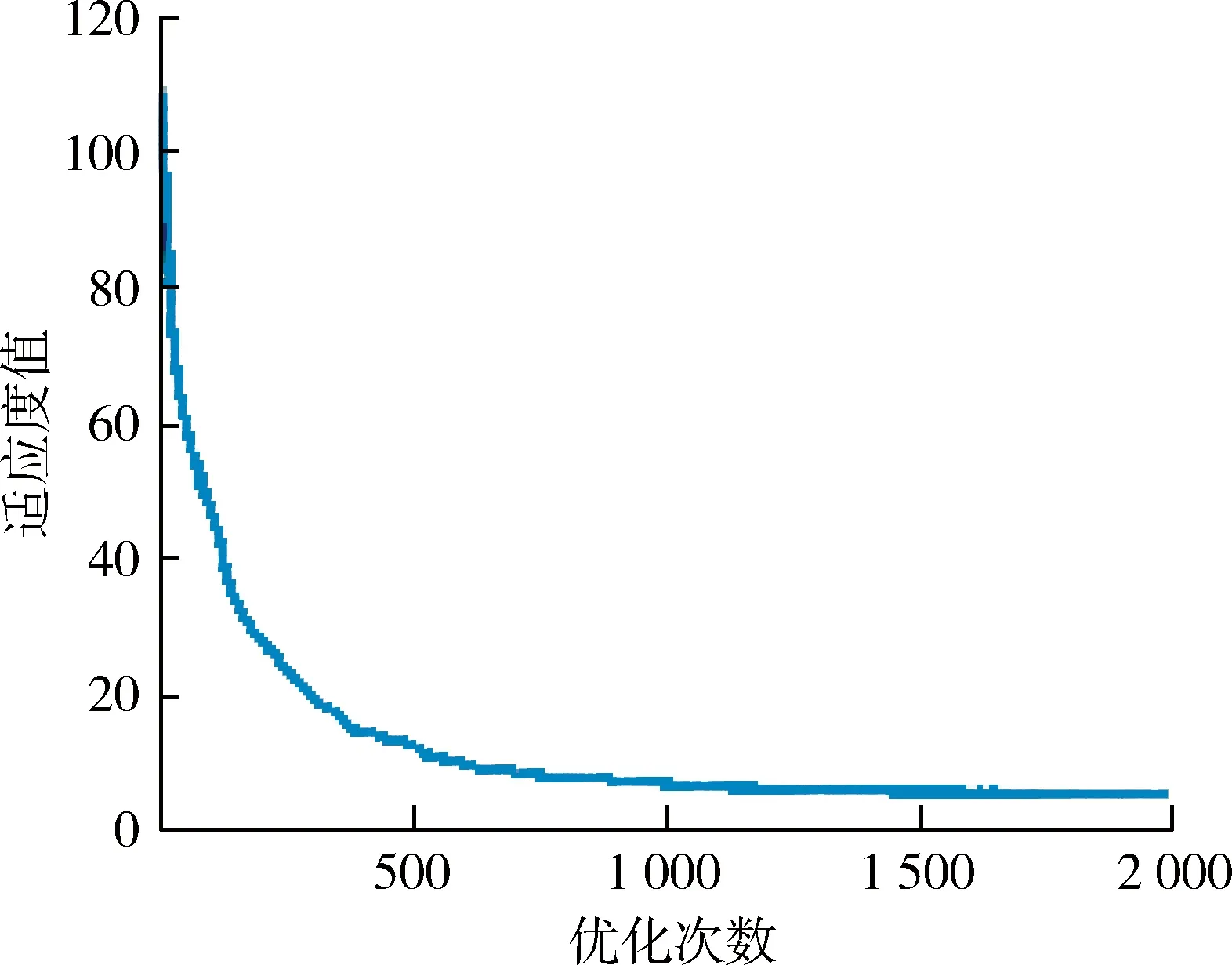
图6 适应度值fw变化曲线

图7 适应度值fp变化曲线
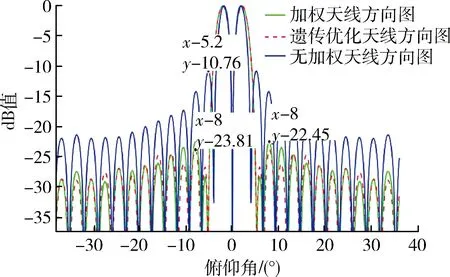
图8 旁瓣电平对比图
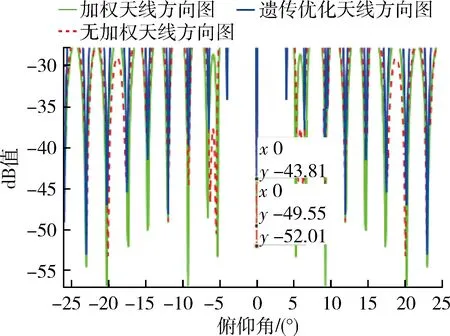
图9 零深对比图

图10 主瓣宽度对比图
图8~10直观展示了在加权和递进型优化算法仿真出的天线方向图,提取天线方向图中的旁瓣电平、波束宽度和零深大小到表1中。

表1 旁瓣电平、零深、主瓣宽度对比表
表1显示,该方案使旁瓣电平降低到-23.81 dB,零深下降到-52.01 dB,比贝叶斯加权方法分别提高了1.36,2.46 dB。表明该算法是有效的,达到提升阵列波束性能的目的。
4 结束语
经过递进型算法对相控阵天线阵列的优化,天线方向图显示相控阵天线阵列内的干扰和误差是可以抑制的,相比于加权优化,该方案具有更强的灵活性,可以使天线方向图按照设定的参数标准去校准。经过对比,该算法的优化效果更佳,算法稳定可靠。本方案可以应用在导引头的检测优化中,使导引头具有更加优异的性能。本课题的进一步研究,可以对相控阵天线阵列多角度检测优化实现整体性能的提升。

