柔性网空中联合组网参数配置优化算法*
贾彦翔,邱旭阳,卞伟伟,刘亮
(北京机械设备研究所,北京 100854)
0 引言
空中柔性拦截网主要用于低空、慢速、微小型航空器(“低慢小”目标)的物理拦截,而利用柔性网在空中的多网联合展开可以大幅度提高柔性网空中有效拦截面积,可提高柔性网对目标拦截的成功率,并可以用于对小型无人机群进行拦截。其有效展开面积大小与对应的时间长短是影响其拦截效能的关键指标。
在拦截网方面,雷江涛等[1]针对单一拦截网防御面积对鱼雷的拦截过程进行了动力学建模与仿真分析,为采用柔性拦截网拦截鱼雷提供了理论参考。空间柔性飞网因能有效避免直接刚性碰撞等优势在空间垃圾处理方面受到广泛关注[2]。很多学者对空间飞网释放展开过程进行了深入研究,如飞网展开过程的动力学模型[3]、网型设计及动力学特性研究[4]、地面抛射试验研究[5]、地面碰撞试验有限元仿真[6]、飞网抛射参数对展开过程的影响研究[7]、空间飞网捕获目标过程的动力学特性[8]和飞网释放动力学与控制方法[9]等。熊自明等[10]对要地近程飞网主动防护拦截系统进行了初步探索,为柔性网的低空实战应用提供了参考,但目前关于低空柔性网动态展开特别是多网联网展开过程的研究相对较少,柔性网低空动力学特性有待进一步挖掘和探索。
多柔性网空中联合组网参数优化配置是一个多目标优化问题,涉及多个优化目标,一般情况下不存在全局最优解[11]。传统的多目标优化算法是基于Pareto支配关系的[12-13],代表性算法有Deb等[14]提出的快速非支配排序算法和Zitzler等[15]采用的Pareto进化算法。Zhang等[16]提出的一种基于分解的多目标优化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D),可在目标空间中生成均匀的权重向量,将多目标优化问题分解成一组单目标优化的子问题,然后通过进化算法同时优化这些子问题,从而得到均匀分布的解空间。
本文建立柔性网动力学模型,并采用MOEA/D对两网联合组合发射、三网联合组合发射、四网联合组合发射的配置参数进行优化设计,以期为柔性网的空中联合组网工程设计提供参考。
1 柔性网空中展开动力学模型
对大变形柔性体的动力学建模一般是采用非线性有限元或者集中质量单元进行求解[17]。从计算精度来看,二者差异不大;从计算速度来看,集中质量单元速度最快。综合计算精度与时间经济性,本文采用集中质量法对柔性网的空中展开过程进行仿真。集中质量法将柔性网离散为一个个的集中质量点,质量点间由等效弹簧和等效阻尼连接,根据离散质量点的相对运动距离和相对运动速度来计算绳段间的张力,如图1,2所示。

图1 柔性网的简化力学模型

图2 绳段单元内力与外力模型
绳段张力为单元弹性力和阻尼力之和,如图2所示,绳段Sij张力的大小为
(1)

等效刚度kij的计算公式为
(2)

绳段sij的等效阻尼cij可表示为
(3)
式中:mij为绳段的质量;ζ为绳段的阻尼比,该参数反映了绳索对能量耗散程度,取值在0~1之间。
设eij为从节点i指向节点j的单位矢量,Con(i)为所有与i相邻的节点集合,则节点i受到的绳索内力可表示为
(4)
绳段Sij受到的气动升力Lij和气动阻力Dij可通过式(5)计算:
(5)

鉴于绳索本身大变形特性,本文采用Williams工程经验公式[18]近似估计绳索受到的气动力。
(6)
式中:αij为绳段的攻角。
设地面风速为vwind,则
(7)
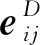
(8)
2 优化算法设计
2.1 优化目标
基于对柔性网在空中展开的动力学模型,对其空中动态展开过程进行分析,设定联合组网的优化目标。
如图3所示,设一无人机目标水平飞行速度为v,其偏航和俯仰运动能够达到的最大加速度为a。定义柔性网最大有效拦截面积为其展开面积在垂直于目标飞行平面上的最大投影,柔性网达到最大有效拦截面积时的网面高度为d,柔性网达到最大有效拦截面积所需的时间为Δt,这里将其定义为柔性网响应时间,柔性网在水平方向运动的平均速度为vNet。若无人机能够在柔性网达到最大有效拦截面积时飞出网面捕获区域则需满足
(9)
即
(10)

图3 柔性网拦截机动无人机示意图
故柔性网响应时间越小,柔性网最大有效拦截面积越大,则对无人机机动能力的要求越高。因此,选取最大展开面积Smax与达到最大展开面积的时间tmax作为柔性网展性能评估指标和优化算法的优化目标。
2.2 优化方法
柔性网联合组网的优化问题是一个典型的多目标优化问题(multiobjective optimization problem,MOP),一般MOP由n个决策变量,m个目标函数和p个约束条件(其中k个不等式约束,q个等式约束)组成,优化的目标如下:
minF(x)=(f1(x),…,fm(x))T,subject tox∈Ω,gi(x)≤0,i=1,…,k,hi(x)=0,i=1,…,q,
(11)
式中:Ω是决策变量空间;F:Ω→Ζ由m个实值目标函数组成,Ζ⊆Rm称为目标空间。
由于式(11)中的目标彼此冲突,决策变量空间Ω中不存在一个点可以使得所有目标同时达到最优。因此,求解MOP的最终目的是在各个优化目标之间进行权衡处理,使所有目标都尽可能达到最优。MOP的解不是唯一的全局最优解,而是一个最优解的集合,称为Pareto最优解集。
MOEA/D的算法框架为:首先选取一组均匀分布的权重矢量w1,…,wN,w为m维向量,N为分解子问题的个数;再选取一个初始最优点z*,z*为m维向量,将原多目标优化问题分解成N个标量优化子问题,其中第j个子问题的目标函数为
(12)
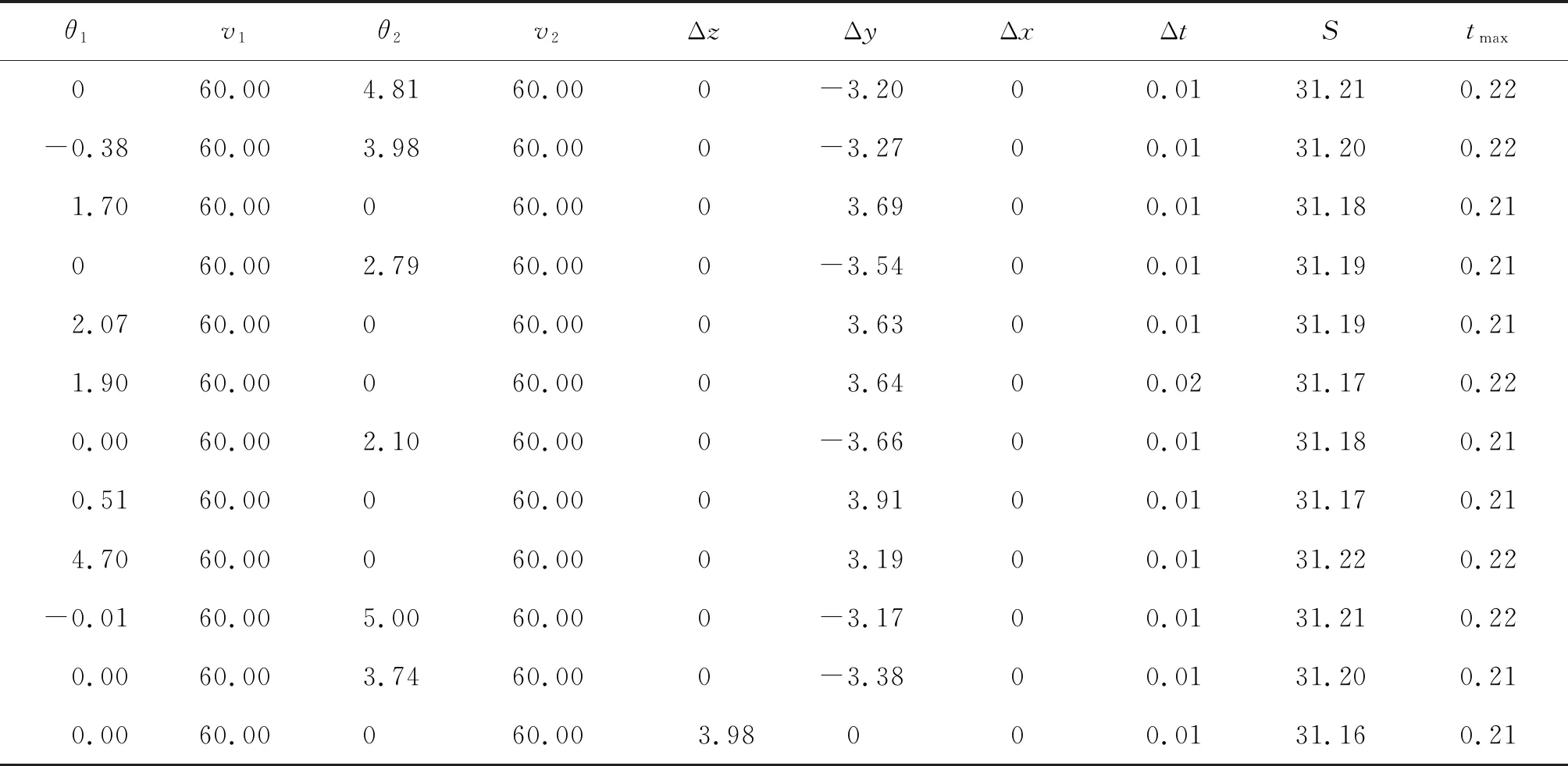
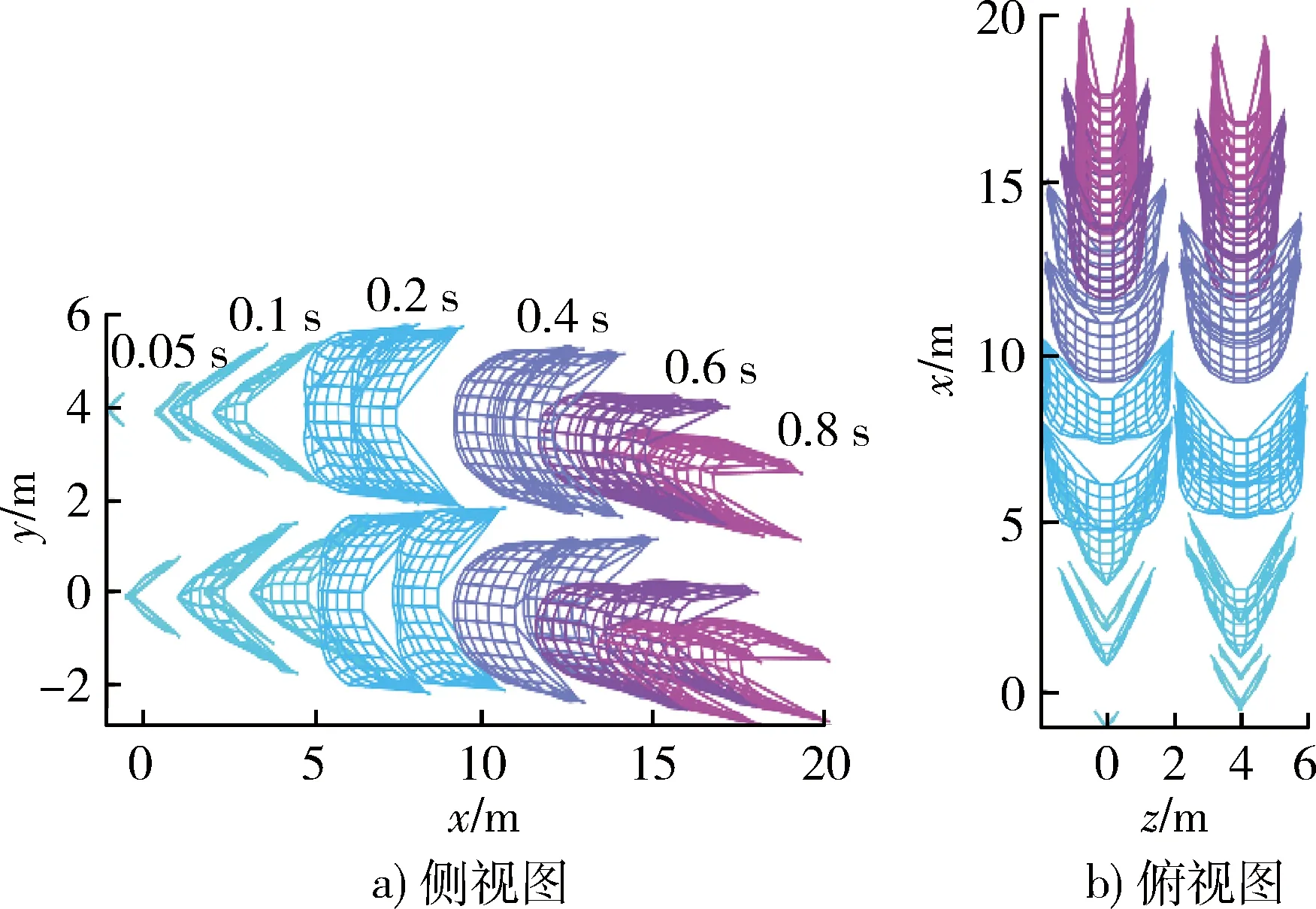
在一次运行中,利用进化算法对N个子问题进行优化。因为gte是w的连续函数,所以若wi和wj彼此接近,那么gte(x|wi,z*)的最优解应该与gte(x|wj,z*)接近,于是与wi相邻的关于gte的任何信息都有助于gte(x|wi,z*)的优化。可以通过向量wi间的欧式距离来衡量2个向量间的接近程度,算法中可以选取距离权重向量wi最接近的T个权重B(i)={wi1,…,wiT}作为wi的邻居,在每次迭代中利用其邻居的信息来辅助gte(x|wi,z*)问题找到最优解。在计算程序中的具体操作为:对于第i个子问题,通过进化算法的变异得到一个新解y,若目前的最优解z满足:zj 多网联合组网的运动过程中要求不同的网之间不发生相互接触,为保证这一点,在算法中设计了罚函数,即在柔性网运动的每一步,若发现任意2张网之间发射接触,则将目标函数的值设为一大数,算法中的设定值是1×1010。 以柔性网空中展开过程为对象,对开网初始时刻,各个网包间的相对位置,各个网包的速度及弹道倾角,每个网之间弹射的延迟时间等开展研究。 对于两网组合,柔性网在空中展开的参数可表示为 X=(θ1,v1,θ2,v2,xr,yr,zr,Δt), (13) 式中:θ1,v1分别为第1发网的网包弹道倾角和速度;θ2,v2分别为第2发网的网包弹道倾角和速度;xr,yr,zr分别为第2发弹相对第1发弹的相对位置;Δt为第2发网相对第1发弹网展开的延迟时间。 三网组合的设计变量为 X=(θ1,v1,θ2,v2,θ3,v3,xr1,yr1,zr1,Δt1,xr2,yr2,zr2,Δt2), (14) 式中:θi,vi分别代表第i(i=1,2,3)发弹的弹道倾角与速度;xr1,yr1,zr1代表第2发弹相对第1发弹的空间相对位置;xr2,yr2,zr2代表第3发弹相对第1发弹的空间相对位置;Δt1代表第2发弹相对第1发弹的发射延迟时间;Δt2代表第3发弹相对第2发弹的延迟时间。 四网联合组网问题的设计变量为 X=(θ1,v1,θ2,v2,θ3,v3,θ4,v4,xr1,yr1,zr1,Δt1,xr2,yr2,zr2,Δt2,xr3,yr3,zr3,Δt3), (15) 式中:θi,vi分别代表第i(i=1,2,3,4)发弹的弹道倾角与速度;xr1,yr1,zr1代表第2发弹相对第1发弹的空间相对位置;xr2,yr2,zr2代表第3发弹相对第1发弹的空间相对位置;xr3,yr3,zr3代表第3发弹相对第1发弹的空间相对位置;Δt1表示第2发弹相对第1发弹发射的延迟时间,Δt2代表第3发弹相对第2发弹的延迟时间;Δt3代表第4发弹相对第3发弹的延迟时间。 在仿真过程中,还需要考虑柔性网空中联合组网过程中的约束情况,这里主要考虑为了缩小搜索空间,对网与网之间的位置进行一定的限制;受到实际物理系统的影响,对网与网之间的发射延迟时间进行一定的限制。 针对水平飞行的目标,基于上述优化算法,得到了两网组合的多目标优化部分解集,如表1所示。从表中数据可见,最大有效拦截面积与柔性网响应时间存在一定的相关性,即同样的参数设置可让最大有效拦截面积达到最大并且使得响应时间最小。 按照表1中的第1行进行参数配置输出,得到两网联合组网的面积-时间曲线,如图4所示,两网组合使得有效拦截面积达到31.21 m2。在联合组网过程中,2张网在铅垂方向的空隙距离如图5所示,在组网面积达到最大的时刻,2张网之间的距离小于0.1 m。联合组网发射展开过程如图6所示,可见,2张网在展开过程中没有相互接触,当网向前飞行10 m左右时达到最大的组网面积。 同两网组合的优化过程类似,三网组合同样会得到多种参数配置下的最优解,根据优化参数配置得到了三网联合组网的展开过程如图7所示。三网联合组网的面积随时间变化曲线如图8所示,三网联合组网的最大面积在0.22 s达到,最大展开面积约47 m2。在三网联合组网的展开过程中,网与网之间的间隔如图9所示,在柔性网达到最大展开面积的时刻,柔性网之间的最大间隔小于0.5 m。 图4 两网联合组网面积随时间变化曲线 与两网、三网组合发射过程相比,优化问题的设计变量维数进一步增大,所得到的解空间也相应的出现了一定的扩展。柔性网四网联合组网的网型变化图,如图10所示。 相比三网联合组网,四网组网发射使得有效拦截面积进一步加大,最大有效拦截面积达到63 m2,如图11所示。网与网之间的间隔如图12所示,从目标飞行方向来看,四张网在铅垂面内的上下间隔和左右间隔具有较好的一致性,在达到最大面积时,四张网的间隔出现了负数,但是由于网与网之间在前后方向上还有一定距离,因此柔性网之间不会发生接触。 图5 两网铅垂面内投影间隔变化曲线 表1 两网联合发射优化计算结果 图6 两网联合组网开网过程 图7 三网联合组网开网过程 图8 三网联合组网面积随时间变化曲线 图9 三网铅垂面内投影间隔变化曲线 图10 四网联合组网开网过程 图11 四网联合组网面积随时间变化曲线 图12 四网垂直方向间隔随时间变化曲线 针对柔性拦截网捕获“低慢小”目标需要,考察多柔性网空中联合组网的运动特点,本文建立了柔性网的力学模型,并基于集中质量法建立了空中开网动力学模型。为了评估多网空中联合组网效能,基于工程实践提出了评价柔性网捕获效果的评估指标。围绕柔性网联合组网发射参数配置问题,引入基于分解的多目标优化算法,对两网联合发射、三网联合发射、四网联合发射问题进行变量设计并进行仿真分析。优化参数配置达到了预期结果,结合相应的约束条件可得到一般的发射参数求取办法,可为柔性网空中联合组网工程参数设计提供参考。2.3 变量设计
3 仿真校验
3.1 两网组合参数校验
3.2 三网组合参数校验

3.3 四网组合参数校验







4 结束语

