膜计算粒子群算法改进极限学习机的水肥预测模型研究*

谢佩军， 张育斌

(1. 浙江纺织服装职业技术学院机电与轨道交通学院,浙江宁波,315211；2. 西安交通大学，西安交通大学机械制造系统工程国家重点实验室,西安市,710054)

0 引言

随着科学技术的日益更新和发展，许多先进的理念与技术被应用于农业领域，快速推进了农业现代化和农业精准化。农业节水理论的研究不断深入和相关技术水平的逐渐提高，农业节水技术正日益走向信息化、精准化，以满足现代农业对灌溉系统的灵活、准确、快捷等要求。水肥气一体化是供氧、施肥和灌溉技术相结合的新技术，按照作物生长各个阶段对养分的需求及气候条件等精准补充水肥气，不仅能够显著提高水肥利用率，还能为土壤提供充足的有效氧，实现作物的增产提质。水肥预测模型是水肥气一体化技术体系中的关键技术，高效、精准的水肥预测模型，能够确保水肥气控制设备科学地调节灌溉水中营养物质的浓度和数量，有效提高作物的产量和质量，还可大幅度提高化肥和农药的有效利用率，减少对农田生态环境带来的污染。水肥预测模型的研究正成为国内外灌溉理论和技术研究有望取得突破点，也对我国农业现代化和农业精准化的发展具有重要意义。

分析智能灌溉技术相关文献发现，水肥耦合及智能控制灌溉研究较多，但基于水肥气集成的多信息融合采集系统、灌溉决策系统的自学习智能系统研究很少，尤其是可供参考、推广的水肥预测模型的研究极少。为了建立高效、精准的水肥预测模型，提出了膜计算粒子群算法优化极限学习机的水肥预测算法，引入膜计算与粒子群算法优化极限学习机。通过获取作物生长期中作物、土壤、天气等实时信息，多信息融合下根据作物的生长状况及营养需求，研究作物水肥用量预测与灌溉决策技术，建立有实际应用意义和推广价值的水肥预测模型。

随着机器学习算法的不断发展，人工神经网络(ANN)[1]、支持向量机(SVM))[2]、随机森林(RF)[3]、高斯过程回归(GPR)[4]、极限学习机(ELM)[5]等逐步被应用于各领域的预测模型。其中ELM具有预测精度高、计算速度快、泛化能力强等优点，结合其他算法广泛应用于非线性过程、观测数据缺乏的预测、评估模型。比如，文献[6]提出了一种基于蚁群算法优化极限学习机，用于预测软件的构件质量，预测模型有较好的灵敏度、准确度和收敛率。文献[7]提出了一种基于蒙特卡罗算法与极限学习机的水电站产能预测模型，预测生产能力和优化能量配置，算法具有较好的准确性和适用性。文献[8]提出一种基于HW方法和极限学习机的住宅用电量短期预测混合模型，将线性预测结果、非线性残差和原始数据作为输入样本进行预测，结果表明该算法构建的模型预测误差较小。文献[9]选择温度、时间、切削速度、进料速度和粒度等工艺因素，利用支持向量机和极限学习机对木材表面涂层的粘接强度进行预测，取得较好的预测精度和效率。文献[10]利用极限学习机通过土壤特征参数进行土壤分类评估，算法具有较好泛化能力和准确度。但由于参数随机选择，导致试验结果过拟合、稳定性不高等问题依然存在。粒子群算法(PSO)具有易于实现和搜索效率较高的优势，粒子群算法与极限学习机融合能够较好地改进极限学习机的不足。粒子群算法优化极限学习机在预测、估计和识别模型中的理论研究与实际应用取得了快速进展，如文献[11]采用混合PSO优化ELM可以有效估算西北干旱区有限气候数据条件下的参考蒸发蒸腾量，文献[12]研究基于PSO和ELM的混合模型能实现环境温度预测以优化能源使用率，文献[13]提出增强型PSO改进ELM可以快速有效地实现电能质量扰动的特征分类，文献[14]提出基于改进型PSO优化ELM模型能够较精确地预测混凝土大坝的变形，文献[15]将PSO改进ELM应用于水电站及水库实现运行规律的高效预测，上述算法均取得一定应用成效，但也存在复杂问题计算时间长、局部搜索能力有限、容易提前收敛等不足。

本文在已有研究的基础上提出了基于膜计算粒子群算法改进极限学习机，利用膜计算的并行性、分布式和非确定性等优点，及粒子群算法的高效搜索性能改进极限学习机，建立膜计算粒子群算法优化极限学习机的水肥预测模型应用于多信息融合的智能灌溉系统。

1 极限学习机

极限学习机(Extreme Learning Machine,ELM)是一种高效的单隐层前馈神经网络(SLFNs)快速学习算法，具有训练参数少、泛化性能好、学习速度快等优点，被广泛应用于农作物产量预测、电力负荷预测、交通流量预测等。

假设有Q个水肥用量的影响因素(平均气温、蒸发量、土壤湿度、日照时间等)作为输入向量样本(Xp,Yp)，其中1≤p≤Q，Xp=[xp1,xp2,…xps]T∈Rs为第p个s维输入样本。以水肥用量预测值作为输出，Yp=[yp1,yp2,…ypr]T∈Rr为第p个r维输出样本，s、r、l分别是输入层、输出层、隐含层的神经元个数。则极限学习机输出水肥用量预测值

(1)

式中：g(x)——激励函数；

Wi——输入层与隐含层间的权值，Wi=[wi1,wi2,…,wis]；

βi——隐含层与输出层间的权值；

bi——隐含层第i个神经元的偏置。

(2)

对应的矩阵表达式

Hβ=Y

(3)

H是隐含层输出矩阵，其表达式为

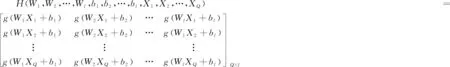
(4)

输出权值矩阵

(5)

期望输出矩阵

(6)

网络训练过程中，当g(x)无限可微时，初始化Wi和bi且保持不变，则利用最小二乘法对式(3)进行求解可得到β[16]。

(7)

式中：H+——H的Moore-Penrose广义逆。

由于输入权值和隐含层偏置的随机性，易产生训练精度和泛化能力的不确定性。针对这个问题，本文采用膜计算粒子群算法优化ELM的初始权值和偏置，改善不稳定性进而提高水肥预测模型的预测精度和泛化能力。

2 膜计算粒子群算法

2.1 粒子群算法(PSO)

粒子群优化算法(Particle Swarm Optimization，PSO)是一种群体智能算法，通过模拟鸟类群体内个体相互之间的迭代信息共享与交流，实现群体全局最优解的搜索。该算法模拟鸟类群体觅食行为，粒子模拟鸟类个体，每个粒子表示一组候选解，不断迭代搜索最优粒子，搜索过程被抽象为具有速度和位置两个属性的粒子飞行过程。

假设D维空间内存在n个粒子的种群，第i个粒子及其位置可表示为Xi=[Xi1,Xi2,…,XiD]T，其速度表示为Vi=[Vi1,Vi2,…,ViD]T。均方根误差(RMSE)能够描述水肥用量预测值和实际用量值之间的偏差，选择RMSE作为适应度函数计算各粒子的适应度值。RMSE值越小则水肥预测偏差越小、预测精度越高，故RMSE值最小即为最佳粒子。第i个粒子的当前最佳值，即个体极值可表示为Pbesti=[Pbesti1,Pbesti2,…,PbestiD]T，种群的当前最佳值，即全局极值可表示为Gbesti=[Gbesti1,Gbesti2,…,GbestiD]T。

当迭代过程找到上述两个极值时，粒子根据式(8)和式(9)更新自身速度和位置

(8)

(9)

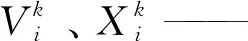
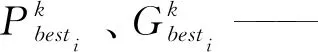
ωi——惯性权重，用于平衡局部寻优能力和全局寻优能力；

c1、c2——学习因子，反映个体极值和全局极值的重视程度；

r1、r2——区间[0,1]内的随机数。

2.2 膜计算

膜计算(Membrane Computing,MC)也称为膜系统、P系统，由罗马尼亚科学家Pǎun[17]于1998年提出，是仿生自然计算的新兴学科分支，从细胞结构及功能、组织器官与细胞群的信息共享、交流抽象而来，膜计算具有分布式、并行性和非确定性等优点。膜计算系统按系统模型结构与规则分为三类：组织型膜系统、细胞型膜系统和神经型膜系统[18]。当前，膜计算理论结合粒子群算法的相关研究也取得了一定进展，可以有效提高算法的寻优能力和收敛速度。

本文提出的膜计算粒子群算法(MCPSO)采用细胞型膜系统，该类型膜系统的基本膜结构如图1所示，将粒子群放入膜系统进行寻优。

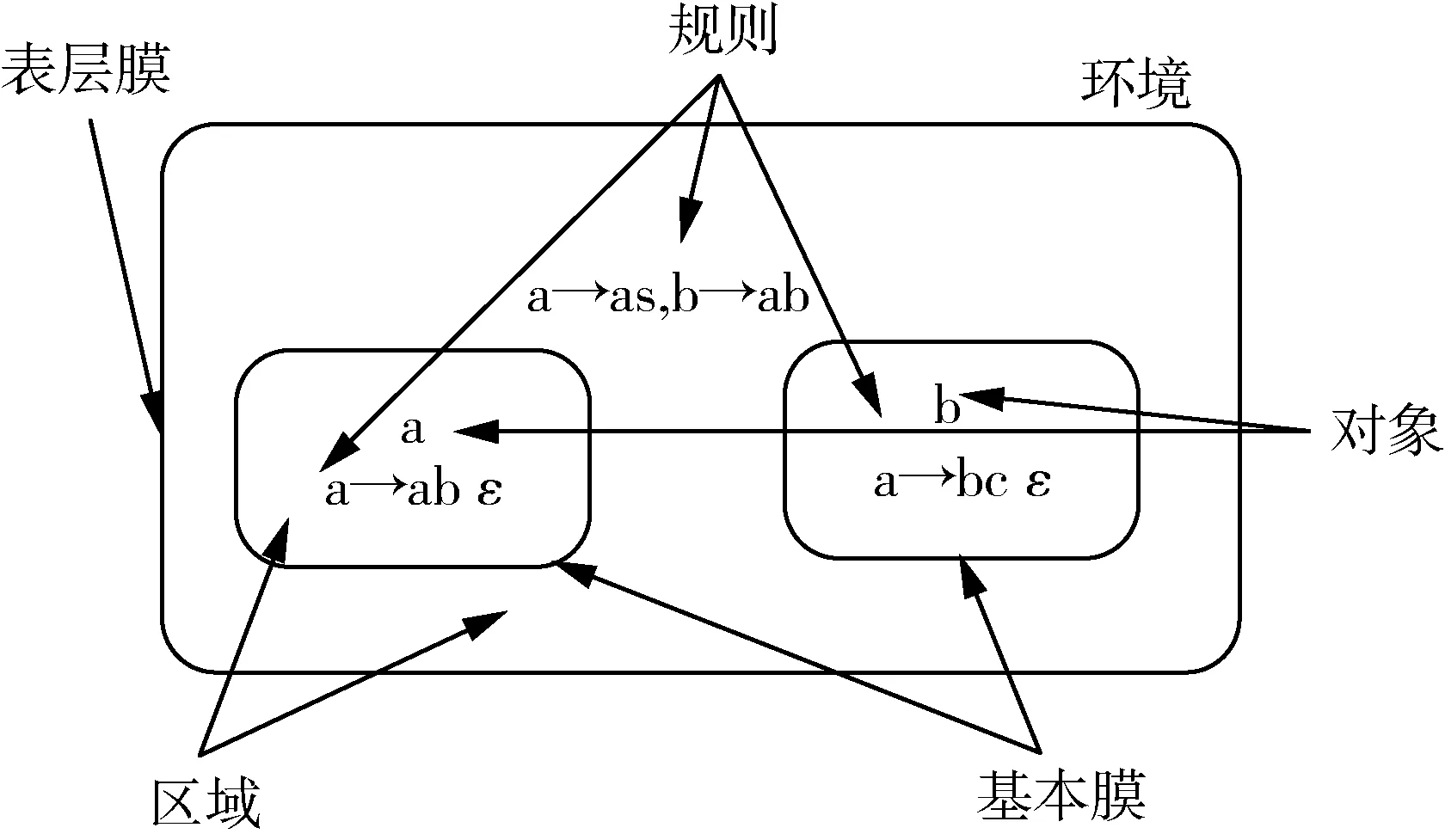
图1 细胞膜结构图Fig. 1 Structure of cell membrane

一个度为的细胞型膜系统的多元组

∏=(V,Σ,H,μ,w1,…wn,R1,…Rm,io)

(10)

式中：V——非空字母表，包含各元素；

Σ——输出对象表；

H——膜标号集合，H={1,2,…,m}；

m——膜系统的度；

μ——包含m个膜的膜结构；

wi——膜区域i内的对象多重集，wi∈V*(1≤i≤m)；

Ri——膜区域i的进化规则，1≤i≤m；

io——系统输出膜。

2.3 膜计算粒子群算法(MCPSO)

本文提出了膜计算粒子群算法，根据所实现的功能不同将膜系统内的生物膜分为主膜和辅助膜两大类。各膜区域i内的对象多重集表示

wi=(X1i,X2i,…,Xni)，1≤i≤5

式中：ni——区域i内粒子个数;

细胞型膜系统一般采用字符型对象，为了保证水肥预测模型可以应用于实际灌溉系统，本算法采用实数变量对象。膜结构包含表层膜膜0和5个基本膜，基本膜包括主膜(膜1)和辅助膜(膜2、膜3、膜4、膜5)，如图2所示。表层膜0不参与具体运算，其功能是收集主膜抛弃的适应度差的粒子。辅助膜的功能是进行搜索空间内的全局搜索，实现最优解区域的寻优，增强种群多样性可以提高全局寻优能力。主膜的功能是在辅助膜实现最优解区域寻优的基础上进行精细化局部寻优，膜内寻优后再加上辅助膜传递来的优势粒子，进行进一步迭代实现全局最优解的搜索。

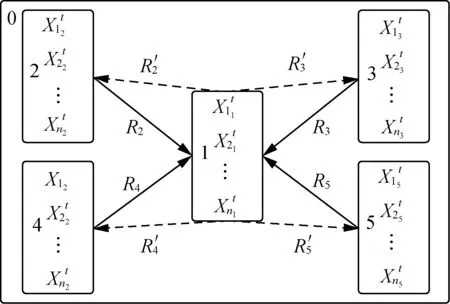
图2 MCPSO膜结构示意图Fig. 2 Membrane structure of MCPSO

种群多样性反映了粒子的聚散程度，本算法将种群多样性引入迭代寻优过程中，从而能够保证良好的全局搜索能力。其表达式为[19]

(11)

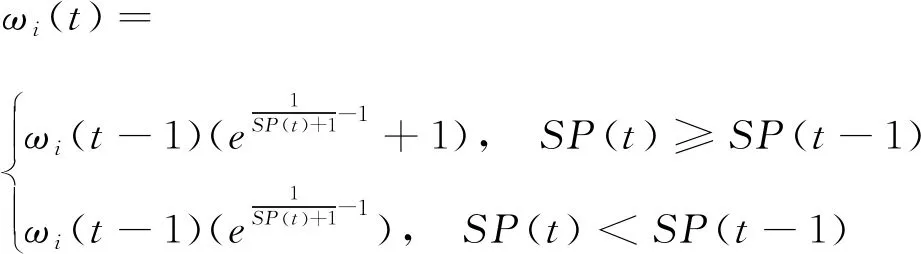
(12)

式中：n——粒子个数；

di(t)——粒子i与其余粒子之间的最小欧氏距离；

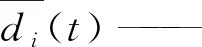
SP(t)——第t次迭代的种群多样性，即粒子群的聚散程度。

SP(t)值变小，说明粒子分布比较均匀、多样性好；反之，则粒子分布不均匀、多样性差。当惯性权重ωi较大时，说明全局寻优能力较强；当ωi较小时，则说明局部寻优能力较强。ωi能够根据SP(t)值的情况相应进行快速调整，从而实现迭代过程中全局寻优能力和局部寻优能力的有效平衡。

膜计算系统具有良好的并行计算能力，所有基本膜能够同时进行各自膜内局部寻优，相当于整个粒子群的全局搜索。辅助膜内的粒子每次迭代过程，根据式(11)计算SP(t)值及数值变化情况来选择式(12)的ωi，粒子的速度和位置按照式(8)和式(9)进行更新，从而保持种群多样性。各辅助膜每迭代一次后，都需要将膜内粒子按适应度值大小进行排序，并将膜内排在前20的优势粒子传送至主膜1。辅助膜传送至主膜的交换规则为

Ri:X′1i…X′20i…X′ni→X′1i…X′20i…X′ni(X′1i…X′20i)in1，2≤i≤5

(13)

主膜膜1的迭代过程同样以式(11)和式(12)确定惯性权重，按照式(8)和式(9)更新粒子的速度和位置。膜1内自有粒子加上辅助膜的80个优势粒子，按适应度值进行排序，将适应度最差的80个粒子传送至表层膜膜0进行抛弃，并将适应度最好的20个粒子进行复制，分别传送至各辅助膜以提高辅助膜的寻优效率。主膜传送至表层膜的交换规则

R1:X′11…X′n1…X′n1+80→X′11…X′n1(X′n1+1…X′n1+80)in0

(14)

其中，X′n1+1…X′n1+80为主膜传送到表层膜进行抛弃的最差粒子。

主膜到辅助膜的交换规则

R′i:X′11…X′n1…X′n1+80→X′11…X′n1(X′n1+1…X′n1+80)ini，2≤i≤5

(15)

2.4 MCPSO-ELM算法流程

本文提出的膜计算粒子群算法优化极限学习机(MCPSO-ELM)算法，利用粒子群算法高效的寻优能力与膜计算强大的平行计算能力，不断迭代优化提高搜索效率和预测精度，引入种群多样性实现迭代过程中全局寻优能力和局部寻优能力的有效平衡，确保算法具有优异的寻优能力和理想的收敛速度。

算法具体步骤如下。

步骤1：确定输入样本，选择水肥用量的6个影响因素平均气温、蒸发量、土壤湿度、土壤肥力、日照时间和作物生育期作为输入向量，并对样本数据进行归一化处理。

步骤2：构建ELM模型，设置激活函数、隐含层单元数等基本参数。设定粒子群寻优参数，包括种群规模、学习因子、惯性权值和最大迭代次数等参数。

步骤3：随机初始化输入权值Wi和隐含层偏置bi。

步骤4：构建膜系统结构，初始化膜内粒子群。根据适应度函数RMSE计算各粒子的适应度值，RMSE值最小即为水肥预测偏差最小的最优粒子，并搜索各膜内个体最优粒子和全局最优粒子。

步骤5：根据相应规则更新各膜内粒子的位置和速度，根据式(11)计算当前次迭代的种群多样性并选择式(12)更新惯性权重。

步骤6：辅助膜通过交换规则将20个优势粒子传送至主膜；主膜接收到各辅助膜的80个优势粒子进行精细化搜索并进行重新排序，将最差的80个粒子传送至表层膜进行抛弃，主膜将前20个粒子回传给各辅助膜。

步骤7：判断是否满足最大迭代次数或小于设定误差，如果满足条件则结束迭代，输出水肥预测精度最高的最优解，并以此建立MCPSO-ELM水肥预测模型；否则，回到步骤5。

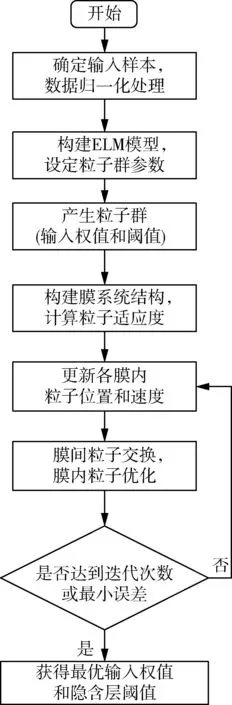
图3 水肥预测MCPSO-ELM算法流程图Fig. 3 Flow chart of water and fertilizer prediction model MCPSO-ELM

3 试验结果与分析

3.1 MCPSO算法性能分析

为了测试MCPSO算法求解复杂问题的性能，进行对比测试分析，文献[20]提出一种改进线性递减惯性权重的非线性递减权重PSO算法(记为WPSO)，文献[21]提出一种线性改变学习因子和动态递减惯性权重的PSO算法(记为IPSO)，均具有较好的搜索速度和寻优性能。选取标准测试函数Rastrigin对PSO、WPSO、IPSO、MCPSO四种粒子算法进行试验，该函数各变量之间无关联且局部最优值随着正弦波动，是一个具有大量正弦拐点排列的局部最优的典型复杂多峰函数

(16)

其中：τ=[τ1,τ2,…,τm]T。设置计算参数：空间维数为2，种群规模为50，学习因子c1∈[1.5,2.5]、c2∈[1.5,2.5]，最大迭代次数为200次，用上述四种粒子群算法分别计算二维空间[-5,5]×[-5,5]内的f(τ)值。各粒子群算法均运行50次取平均值，运行结果对比如表1所示。

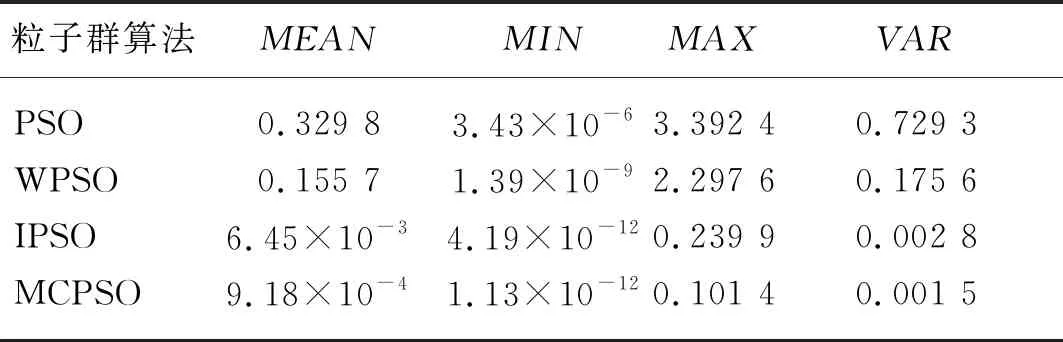
表1 四种粒子群算法的测试结果Tab. 1 Test results of four particle swarm

根据表1内四种粒子群算法运行结果的均值(MEAN)、方差(VAR)、标准差(SD)等进行对比分析，WPSO、IPSO和MCPSO的各项测试值均优于标准PSO测试值，说明三种改进算法均能提升算法性能，MCPSO的各项测试数据远远小于其他模型的测试数据，说明算法寻优效果更好，性能更加稳定，模型抗噪能力更强。MCPSO算法以膜系统的高效平行计算能力优化粒子群，更快找到个体最优、收敛到全局最优解，提升模型的收敛速度与预测精度。

3.2 试验方案

作物水肥用量的影响因素较多，为了简化网络模型及优化预测计算过程，选取平均气温、蒸发量、土壤湿度、土壤肥力、日照时间和作物生育期6项影响因素[22-23]作为水肥预测模型的输入向量，以水肥混合液用量作为输出值。利用MCPSO-ELM算法建立分类器，通过样本数据训练学习，并将预测结果与实际值进行对比分析。

水肥用量上述影响因素的原始数据量大，若直接用于模型计算训练，则数据处理时间长，严重影响模型运行效率，且在不同程度上影响模型的预测精度和算法鲁棒性。因此，需要将原始数据归一化处理至区间[0,1]。

水肥预测模型表达式

(17)

式中：YP——水肥用量；

T——平均气温；

E——蒸发量；

M——土壤湿度；

F——土壤肥力；

S——日照时间；

G——作物生育期；

r——辐射修正系数；

Δ——饱和蒸气压曲线斜率；

η——土壤有效养分系数。

选用2017年3—8月“甬甜5号”(春季甜瓜)的观测数据作为训练样本集，2018年3—8月的观测数据作为测试样本集。3月19日移苗施基肥，3月21日移栽定植，4月19日伸蔓期追肥，5月10日膨瓜初期追肥，6月7日甜瓜成熟。甜瓜整个生育期的氮磷钾用肥量比例为4∶2∶3，在移栽前完成基肥穴施，施用量为40%氮肥(尿素)、40%钾肥(硫酸钾)及70%磷肥(过磷酸钙)，剩余用肥通过水肥滴灌系统进行施肥，以田间持水率75%为灌水下限。建立四种预测模型：PSO-ELM模型、WPSO-ELM模型、IPSO-ELM模型与本文提出的MCPSO-ELM模型进行对比分析，为了简化数据及提高模型可靠性，模型对苗期到成熟期的水肥用量进行预测。

3.3 模型评价指标分析

为了验证MCPSO-ELM模型的运算效率与预测性能，采用标准性能评价准则对上述四个模型进行性能评价，选用平均绝对误差MAE、均方误差MSE和自相关系数R2等3个误差度量来检测，进而对比分析各模型预测性能的优劣[24]。本文对MCPSO-ELM模型、PSO-ELM模型、WPSO-ELM模型、IPSO-ELM模型及ELM模型实施对比试验，样本进行50次训练，取平均值作为最终计算结果。MAE和MSE值越小，则预测模型的预测偏差越小、精度越高；R2值越接近于1，则预测值与实际值吻合度越高。

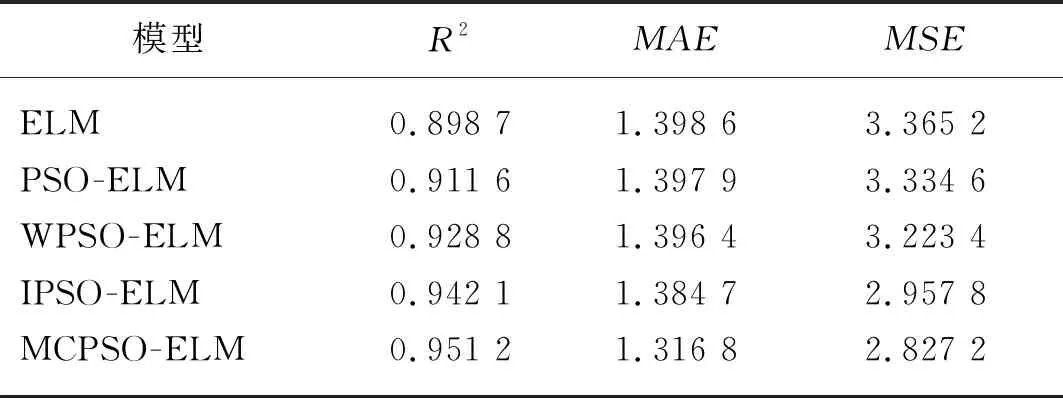
表2 模型预测评价指标对比分析Tab. 2 Comparative analysis of evaluation indexes

根据表2的模型评价指标来分析，各模型都能较准确地预测水肥用量。ELM模型的自相关系数R2最小，其他模型均采用不同的粒子群算法改进极限学习机提升了R2值，说明粒子群改进极限学习机能够有效提高模型的预测精度；MCPSO-ELM模型的自相关系数R2最接近1，说明其预测精度最高；MCPSO-ELM模型的MAE及MSE值均不同程度地小于其他模型，进一步说明本文所提出改进策略的正确性，通过膜计算和粒子群算法能够有效提高极限学习机的预测精度，优化模型的泛化能力。

3.4 水肥用量预测结果分析

2017年3—8月“甬甜5号”的观测数据作为训练样本集对四种模型进行训练，2018年3—8月的平均气温、蒸发量、土壤湿度、土壤肥力、日照时间和作物生育期等影响因素作为水肥预测模型的输入向量，通过各模型计算输出该生育期水肥用量的预测值，将预测结果与实际值进行对比分析，如图4、图5所示。从水肥用量实际值与各模型的预测值对比图来看，四种模型的预测数据总体上与实际水肥用量的变化趋势曲线能够基本吻合，可见各模型均具有一定的预测能力。但从预测数据与实际水肥用量数据曲线的拟合度进行分析，PSO-ELM模型、WPSO-ELM模型和IPSO-ELM模型的预测数据值与实际值存在不同程度的偏离，PSO-ELM模型的偏离程度最大，预测数据不稳定；WPSO-ELM模型和IPSO-ELM模型的部分预测数据能够贴近实际值，拟合度和数据稳定性优于PSO-ELM模型；MCPSO-ELM模型的预测数据能够保持最佳的拟合度和数据稳定性，说明MCPSO-ELM模型预测性能比其他三个模型更好。

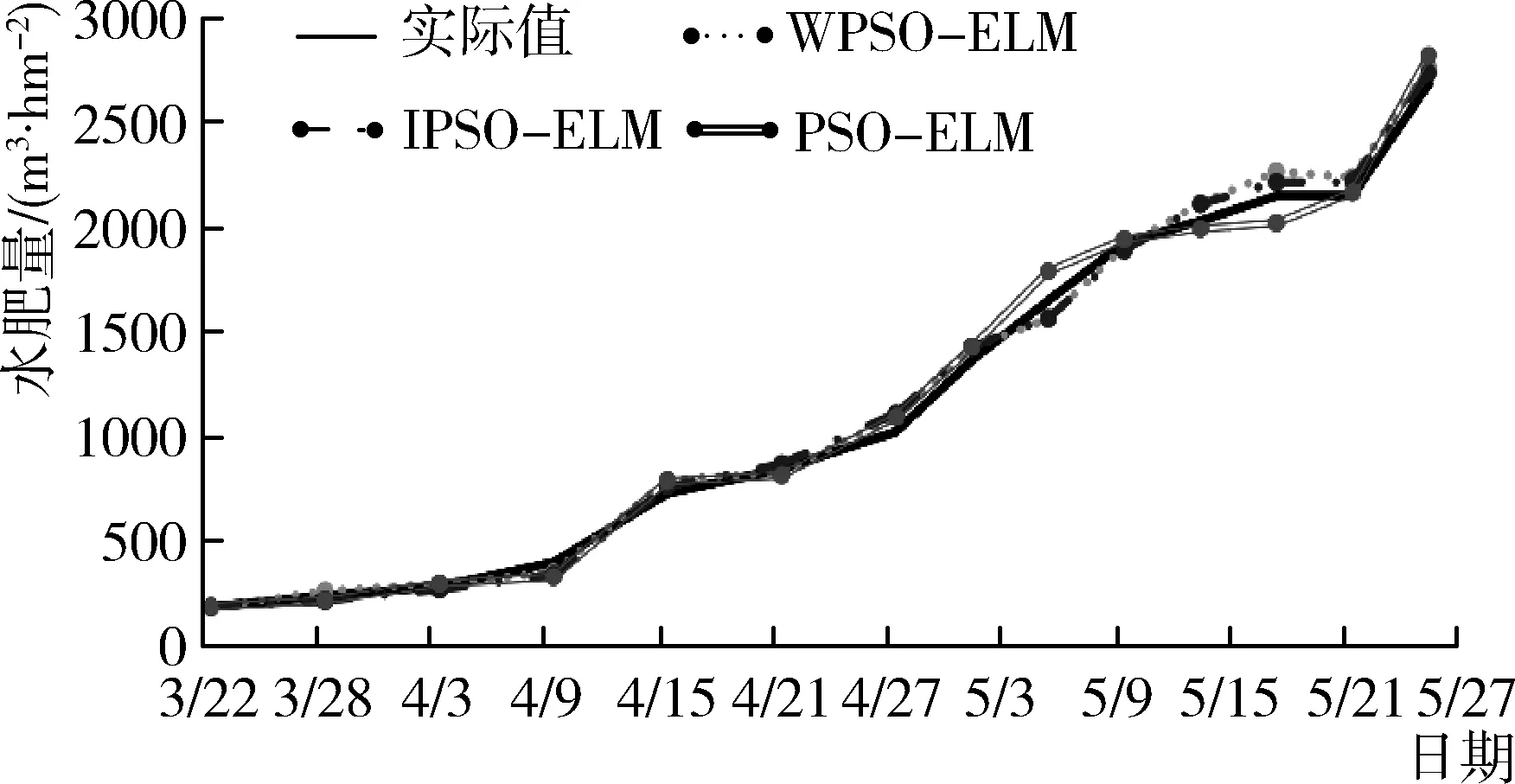
图4 水肥用量实际值与WPSO-ELM、IPSO-ELM、PSO-ELM预测值对比图Fig. 4 Comparison chart of actual value and predictive value of WPSO-ELM, IPSO-ELM and PSO-ELM

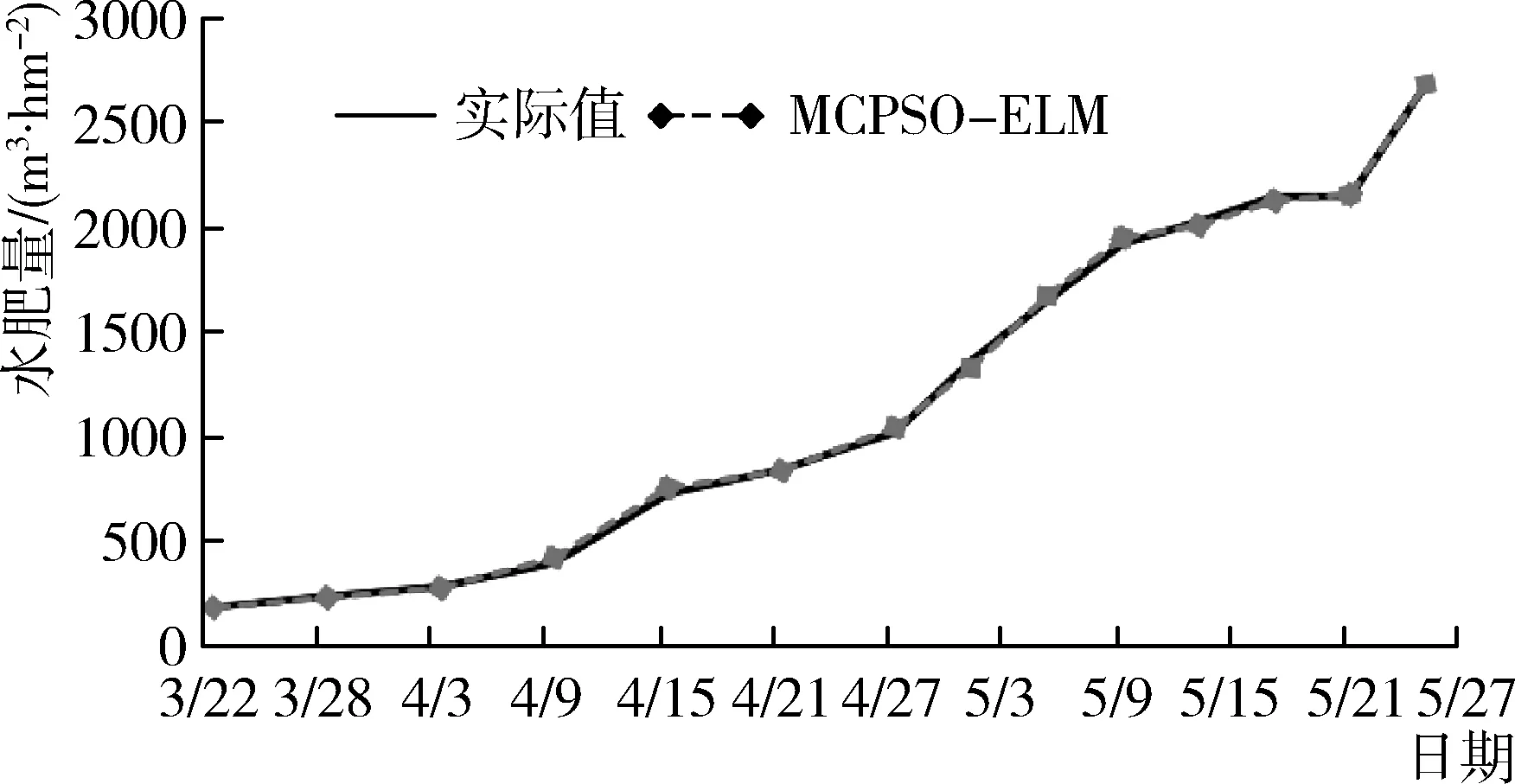
图5 水肥用量实际值与MCPSO-ELM预测值对比图Fig. 5 Comparison chart of actual value and predictive value of MPSO-ELM

为了进一步分析模型的预测精度与数据稳定性，根据各模型预测值(PVi)和水肥用量实际值(RVi)分别计算预测误差PEi=PVi-RVi，相对误差REi=|PEi|/RVi和平均绝对百分比误差(MAPE)。

(18)

从图6中各模型的预测误差和表3相对误差对比分析可知，PSO-ELM模型的预测数据误差值达到±140 m3/hm2左右，最大相对误差17.6%，MAPE达5.6%；IPSO-ELM模型的预测数据误差值降到±100 m3/hm2左右，最大相对误差14.8%，MAPE为5.1%，预测能力比PSO-ELM模型和WPSO-ELM模型更强；而MCPSO-ELM模型预测数据误差值保持在±30 m3/hm2之内，最大相对误差6.4%，MAPE为2.0%，误差波动最小，预测精度得到大幅度提升，完全能够满足水肥预测要求。综合分析模型预测数据与实际水肥用量曲线的拟合度，并对比分析模型预测误差可知，MCPSO-ELM模型的能够有效提高收敛速度、强化学习能力，模型的预测精度和数据稳定性均优于其他模型，预测结果更接近真实水肥用量数据。

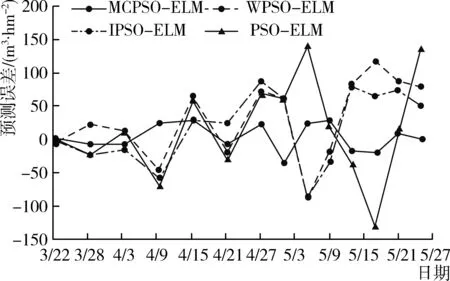
图6 各预测模型的预测误差对比图Fig. 6 Comparison chart of the prediction errors of models

表3 各预测模型的相对误差对比表Tab. 3 ComparisonTable of the relative error of models

4 结论

灌溉系统的水肥用量受作物生育期内平均气温、土壤湿度、日照时间等因素的综合影响，因此，水肥预测存在数据计算量大、预测难度大、预测精度不高等问题。高效的水肥预测模型能够确保灌溉系统科学地调节水肥比例与用量，大幅度提高农作物的品质和产量，提升化肥和农药的有效利用率，减少农田生态环境的污染。

1) 为了建立高效、精准的水肥预测模型，本文提出了膜计算粒子群优化极限学习机的预测算法，利用粒子群算法的高效率搜索能力与膜计算的平行计算优势，引入种群多样性有效解决了全局搜索和局部寻优之间的平衡，算法具有理想的收敛速度和优异的寻优性能，提升了极限学习机的计算速度、泛化能力和预测精度。

2) 建立了MCPSO-ELM模型、WPSO-ELM模型、IPSO-ELM模型和PSO-ELM模型，采用“甬甜5号”(春季甜瓜)不同年份的观测数据对预测模型进行有效性验证，根据模型预测数据拟合度和模型预测误差进行综合对比分析。MCPSO-ELM模型的预测误差小于30 m3/hm2，其他模型基本都大于100 m3/hm2；MCPSO-ELM模型预测数据最大相对误差6.4%，MAPE为2.0%，误差波动最小，其他模型的MAPE均大于5.0%，因此，MCPSO-ELM模型的预测曲线与水肥实际用量曲线最为接近，模型预测性能更优秀。

3) MCPSO-ELM模型能够有效提高收敛速度、强化学习能力，模型的预测精度和数据稳定性均优于其他模型，能够根据作物生育期的影响因素数据实现水肥用量的精准预测，为多信息融合的智能水肥气灌溉系统提供支持。