土壤墒情预测相关性数据耦合性试验分析*

安小宇，赵复兴，柳海涛

(郑州轻工业大学电气信息工程学院，郑州市，450002)

0 引言

我国是一个水资源非常缺乏的国家，同时农业用水又占据了很大的比例[1]。在有限的资源下，改善农作物的生长状态，就需要不断提高灌溉技术[2]。提高墒情预测的精确度，对农作物的生长起到至关重要的作用，并对我国的水资源做出了巨大的贡献[3]。因此，对墒情的研究是近些年相关科研机构的重要课题之一[4]。

段浩等[5]提出在遥感Penman-Monteith模型中土壤含水量与土壤蒸发量的关系，通过运用遥感的方法对蒸发量进行试验，验证了土壤含水量的变化与土壤蒸发量之间的关系；Scott等[6]通过饱和的含水量和蒸腾系数建立了土壤墒情变化的模型，验证了蒸腾因素对土壤含水量的影响；刘小刚等[7]将时间序列分析法与ArcGIS普通克里金差值法相结合的方法对墒情变化情况进行试验，得出了墒情变化与大气环境之间的联系；Schmer等[8]通过监测到的环境数据进行研究，得出了墒情与地表温度间的耦合关系；裴源生等[9]以满足水资源实时调度模型系统的需求为目标，结合地表因素、大气环境因素和人工灌溉因素的空间分布情况，得出对墒情变化造成的实时影响；Wilson等[10]通过对温度与墒情之间相互关系的研究，得出墒情的季节性变化规律和每日温度变化的关系；Lin等[11]采用土壤水动力的研究方法，得出农作物种植条件的变化对墒情的影响。

传统的方法对墒情进行预测时，都会考虑到影响墒情变化的各种变量，这样就会增加墒情预测的难度、增加预测的时间同时降低预测的精确度。本文首先采用相关性分析法，来得到墒情的变化与其它变量的耦合大小，然后通过ROC曲线分析得出在有无降水状态下的阈值，进而通过卡方分析，分别得出在有无降水状态下墒情与其它变量之间的耦合关系，最后通过线性回归分析和BP神经网络进行试验对比，为提高墒情预测的准确率提供技术参考。

1 材料与方法

1.1 试验材料

本文是针对河南省平顶山市的农田环境进行分析试验，该城市处于中国华东地区，属于温带大陆季风性气候，平均海拔高度为400 m。从该地区采集到的农田环境变量有：蒸发量、地温、降水、气压、土壤相对湿度(墒情)、日照时数、气温、风速。实测数据为2019年3—9月的数据，其中3—9月有降水为57 d(26.64%)，无降水为157 d(73.36%)，总数据(N)为214组。

1.2 试验工具

本试验所使用的数据库借助Excel录入各种数据，然后使用SPSS17.0统计软件对所录入的数据进行试验分析，得出最终的试验结论。在录入墒情和大气环境的数据后，针对有无降水的状态进行分析检验，检验水平为P<0.05(P为显著性程度)。

1.3 试验方法

本文首先采用Pearson相关系数法，得出墒情与各变量之间的相关系数，然后使用ROC曲线来对有无降水两种情况进行分析，分别得出在这两种情况下各个变量的阈值，而后通过卡方分析得出在有无降水状态下的卡方值，最后利用线性回归分析和BP神经网络，来对有无剔除与墒情变化相关性较小的变量进行试验对比，得出在剔除相关性较小的变量后，对墒情的预测更加显著。

1.3.1 Pearson相关分析

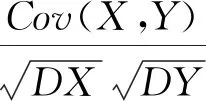
(1)

式中：EX——X的平均值；

EY——Y的平均值；

N——数据的总量；

RX,Y——相关系数。

1.3.2 ROC曲线分析

受试者工作特性曲线(ROC曲线)分析主要对诊断的阈值进行修正，获得多对真(假)阳性率值。在ROC曲线下面的面积称做AUC值，用来判断诊断试验的可靠性[13]。通常认为AUC的值在0.5～0.7之间时，诊断的可靠性较低；在0.7～0.9之间时，诊断的可靠性中等；大于0.9时诊断的可靠性较高[14]。

本文提出ROC曲线分析是来区分在有无降水两种情况下，各变量对墒情变化的影响程度。即在有雨状态和无雨状态两种情况下，来分析影响墒情变化的主要因素。根据试验的有关数据，对有雨组和无雨组进行判定分析，得出在不同状态下的临界值，并且对不同状态下各变量的坐标分布进行计算，同时以此状态的敏感性做为纵坐标代表真阳性率，特异性作为横坐标代表假阳性率，来对ROC曲线进行绘制。

1.3.3 卡方检验

卡方检验是一种假设性检验的方法之一，用来检验两组或两组以上的样本率之间的差别、变量与变量之间有无相关性等方面的问题[15]。卡方检验是在ROC曲线分析后的第一次检验，根据ROC得出的阈值来划分土壤的高低墒情，然后对所有试验数据进行分类，从而得出期望值E(r)；测得的实际值为O(r)，从而根据式(2)得出各变量与墒情之间的卡方值。

(2)

当r为1项集时，E(r)=O(r)，则式(2)转为式(3)。

E(r)=N×E(r1)/N×…×E(rk)/N

(3)

卡方检验就是判断土壤数据实际的测试值与理论值的偏差程度，卡方值的大小就表示测试值与理论值的相关性程度[16]。

1.3.4 线性回归分析

线性回归分析在统计学中，使用线性回归方程的最小平方函数对一个或多个自变量的变化情况，来预测与之相关的某变量的未来值，而建立的一种分析方法[17-18]。本文以墒情作为因变量Y，影响墒情变化的各个变量作为自变量X，建立线性回归模型如式(4)所示。通过线性回归分析，来对比在有无剔除与墒情变化相关性较小变量时的预测误差，从而得出在墒情预测时的更优预测模型。

Y=β0+β1X1+β2X2+…+βn·Xn+ε

(4)

式中：Y——墒情值；

β0——常量；

ε——残差；

Xi——影响墒情变化的各个变量，i=1，2,3…n；

βi——影响墒情的变量Xi的系数。

1.3.5 BP人工神经网络

截止到目前为止，使用最为广泛的神经网络是BP算法的多层前馈网络，在许多非线性的模型中，BP算法可以较为准确的反应出变量与变量之间的关系[19]。常用到的BP结构如图1所示，由输入层、隐含层、输出层组成。

图1 BP神经网络结构Fig. 1 BP neural network structure

本文将影响墒情变化的7个变量作为输入层，墒情作为输出层，隐含层的节点数目由式(5)进行计算，由式(5)得出本试验隐含层节点数范围为4～13。

(5)

式中：M——输入层节点数；

L——输出层节点数；

a——整数，1～10。

本文采用试算法来对隐含层节点数进行确定。表1列出了隐含层不同节点个数下的训练情况，可以看出，相对误差的变化不大，而决定系数R2的变化较大，而隐含层节点数为9时，R2最小，从而确定隐含层节点数为9。最终确定BP神经网络的拓扑结构为7∶9∶1。

表1 不同隐含层节点数模型训练的表现Tab. 1 Performance of different number of neurons in the hidden layer under training

本文将影响墒情变化的各变量作为输入层，随后在隐含层进行算法处理，将经过处理后的数据与真实数据进行对比，若其差值不满足设定的精度要求，则进入反向传播，此时各层神经元的权值、阈值将进行改变，通过以上过程循环不断对权值、阈值进行改变，直到满足设置的最小差值或者预设的训练次数[20-21]，其过程如下。

1) 参数初始化。首先设置网络输入层、隐含层、输出层节点数为M、q、L，其次初始化各个神经元层之间的权值、阈值。

2) 正向传播算法。隐含层输出如式(6)所示。

(6)

式中：Hi——隐含层输出；

j——输入层；

i——隐含层；

ωij——输入层与隐含层连接权值；

a——隐含层阈值；

f——隐含层激励函数。

把得出的Hi作为输出层的输入值，进而对输出层进行计算。输出层的输出如式(7)所示。

(7)

式中：Ok——输出层输出；

bk——输出层阈值；

ωki——隐含层与输出层连接权值。

3) 输出O与期望y′k的误差如式(8)所示。

ek=y′k-Ok,k=1,2,…,L

(8)

式中：ek——第k个节点输出与期望的误差。

4) 权值、阈值的更新如式(9)～式(12)所示。

(9)

更新输入层与隐含层之间的连接权值，得出下一次神经元的连接权值。

ωki=ωki+ηHiek,i=1,2,…q;k=1,2,…,L

(10)

更新隐含层与输出层之间的连接权值，得出下一次神经元的连接权值。

(11)

更新隐含层的阈值，得出下一次神经元的阈值。

bk=bk+ηek,k=1,2,…L

(12)

更新输出层的阈值，得出下一次神经元的阈值。

式中：η——学习效率。

5) 返回步骤(2)，更新过权值与阈值后重新计算各神经元输出值，当输出误差小于设定误差时，保留当前权值与阈值，否则重复以上过程直到输出误差满足为止。

通过BP神经网络，来对比在有无剔除与土壤墒情变化相关性较小变量时的预测误差，从而得出在墒情预测时的更优预测模型，同时与线性回归分析的预测结果进行对比，来验证本试验的准确性。

2 试验结果与分析

2.1 Pearson结果分析

本文首先对传感器采集的所有数据进行相关分析，得出墒情与各变量之间的相关性数值，如表2所示。从表2中可以看出，相对湿度与蒸发量的相关系数最大为-0.534，呈负相关，并且显著性程度P<0.05，相对湿度与降水、地温、气压、日照时数、风速呈相关性，同时显著性程度P<0.05。气温与相对湿度的相关性较弱，为0.018，把该变量作为墒情预测时拟剔除的变量。

表2 Pearson相关性分析结果Tab. 2 Pearson correlation analysis results

2.2 ROC曲线结果分析

在有无降水两种状态下，对土壤墒情做进一步的ROC分析。图2为在有雨状态下的ROC曲线，从图2中可以看出在有雨状态下，降水的ROC曲线下的面积最大。

在表3中可以看出，在有雨状态下，降水量的AUC值为1，相对湿度的AUC值为0.851，而其余几个变量的AUC值都小于0.5，故在有雨状态下，相对湿度的变化只与降水量有较大的相关性。在表3中还列出了各变量在有雨状态下ROC曲线的标准误差和显著性的具体数值。在无雨状态下的ROC曲线如图3所示。

图2 有雨状态下的ROC曲线Fig. 2 ROC curve under rain condition

表3 有雨状态曲线下的面积Tab. 3 Area under rain state curve

图3 无雨状态下的ROC曲线Fig. 3 ROC curve under non rain condition

从图3中可以看出在无雨状态下，日照时数、蒸发量、地温、气压的ROC曲线下的面积相对较大。在表4中可以看出，在无雨状态下，蒸发量的AUC为0.656，P<0.001；地温的AUC为0.637，P<0.01；日照时数的AUC为0.814，P<0.001；气温的AUC为0.589，P<0.05，故在无雨状态下，相对湿度的变化与蒸发量、地温、日照时数有较大的相关性。

表4 无雨状态曲线下的面积Tab. 4 Area under rain-water condition curve

最终根据ROC曲线可以得出在有无降水两种状态下每个变量的阈值，如表5所示，进而来为卡方分析提供一个标准阈值，进一步得出与墒情变化的相关性较大的变量。

表5 分类后的阈值Tab. 5 Thresholds for classification

2.3 卡方检验结果分析

根据ROC曲线得出的每个变量的阈值进行卡方分析，其中，降水量1表示有降水，0表示无降水。分别对每个变量在高墒值和低墒值两种情况下进行分类分析，即在高墒情况下，大于或者小于各个变量的阈值划分情况如表6所示，从表6中可以看出蒸发量的卡方值最大，为67.608，则显著性最强，说明蒸发量越大对墒情的影响就越大；其次是日照时数，卡方值为39.731，显著性为0.001，说明日照时间越大，对墒情的影响越大；气温的卡方值最小，为1.385，显著性为0.275，表示气温与土壤墒情不显著相关。经过表6分析可得，与墒情变化相关性较大的变量有蒸发量、地温、气压、日照时数和风速。

表6 卡方分析结果Tab. 6 Chi-square analysis result

2.4 线性回归结果分析

通过线性回归来对土壤墒情进行预测，表7～表9为在未剔除与墒情变化相关性较小的变量时的分析结果，以此来与本文第2.5节进行对比。从表7中可以看出，回归分析的Sig值为1.557 2e-32，从表8中可以看出，线性回归模型预测的标准偏差为13.229 5，残差为11.895 9，表9为各变量的回归系数。图4为墒情的回归标准化的正态分布图，从图4中可以看出试验所用的数据呈正态分布，说明试验分析有效。

表7 线性回归方差分析Tab. 7 Variance analysis of linear regression

表8 线性回归残差统计Tab. 8 Residual statistics of linear regression

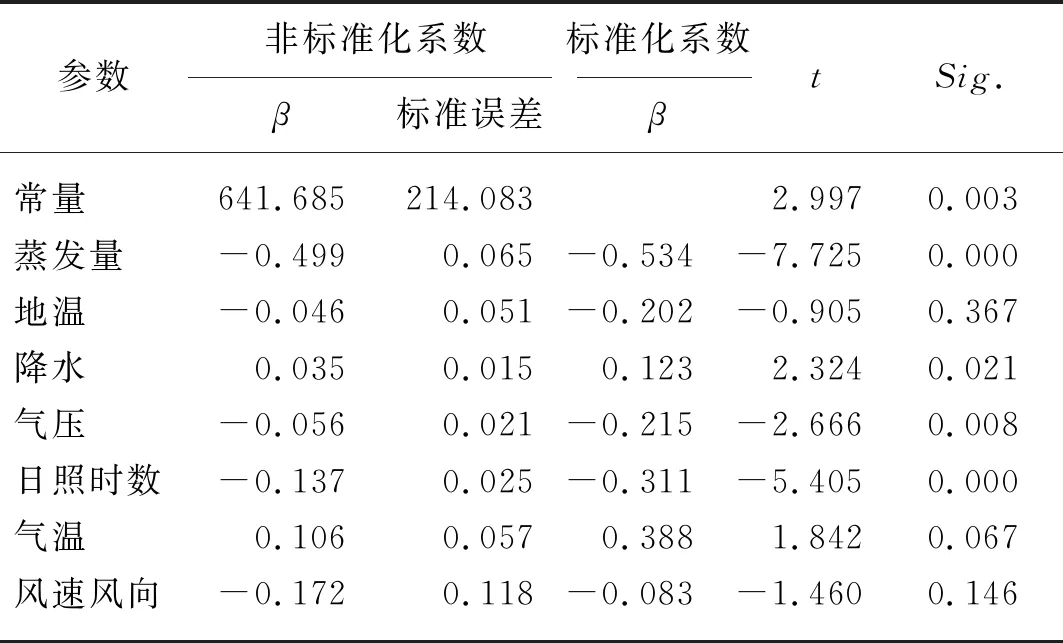
表9 线性回归回归系数Tab. 9 Regression coefficient of linear regression

图4 相对湿度的正态分布图Fig. 4 Normal distribution diagram of relative humidity

2.5 降维后的线性回归对比分析

经过剔除相关性较小变量的方差分析和线性回归系数的分析如表10所示，从表中可以看出，线性回归的显著性值为9.606e-33，而未剔除相关性较小的变量的显著性值为1.557 2e-32，说明在剔除相关性较小变量后的显著性更好。表11为剔除相关性较小变量的残差统计表，从表中可以看出经过剔除相关性较小变量之后的预测值的标准偏差为12.888 3，残差为12.264 7，而未经过剔除相关性较小变量的预测的标准偏差为13.229 5，残差为11.895 9。由此可见，经过剔除相关性较小的变量之后，对墒情预测的准确性更为有利。表12为剔除相关性较小变量后的回归系数。

表10 剔除相关性较小变量后的方差分析Tab. 10 Variance analysis after the elimination of

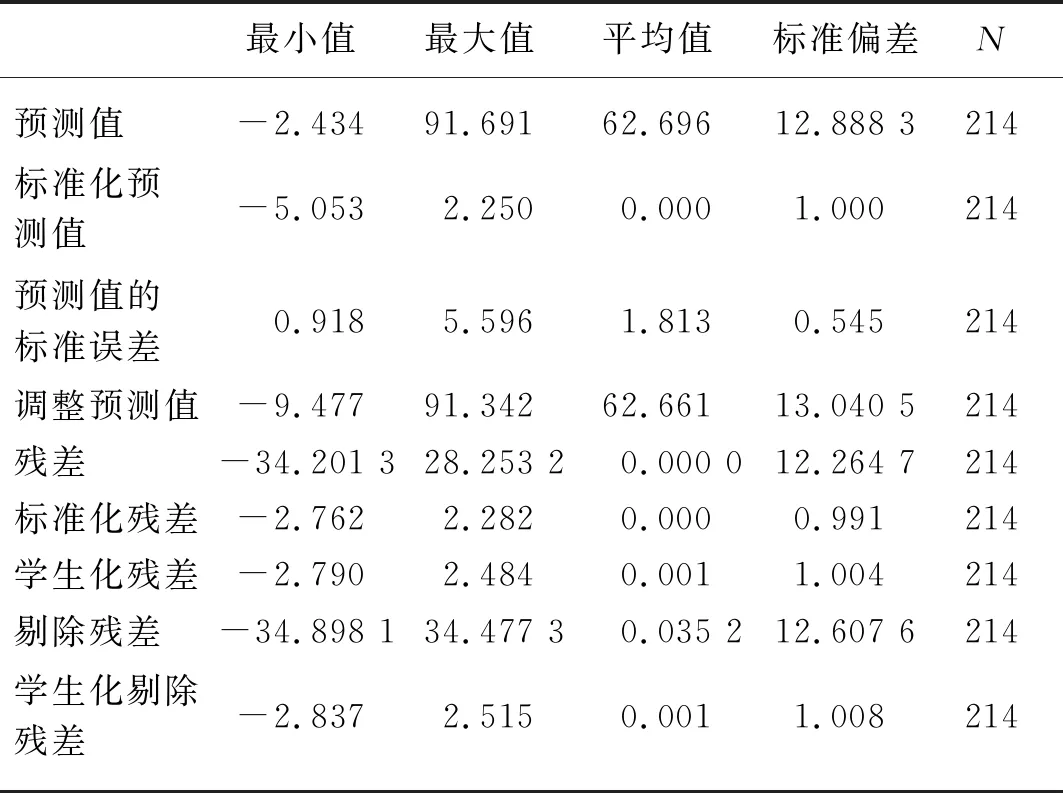
表11 剔除相关性较小变量后的残差统计Tab. 11 Residual statistics after the elimination of

表12 剔除相关性较小变量后的回归系数Tab. 12 Regression coefficient after the elimination of

2.6 BP神经网络预测结果分析

为了综合体现BP预测模型的性能，通过绝对误差的平均值(PING)、方差(VAR)、相对误差的平均值(Relativeerror)三个指标来评价预测结果，在无剔除相关性较小的变量时，BP神经网络预测后的相对误差为0.004 9，平均误差为0.024 4，方差为3.248 9×10-4，如表13所示。在删除相关性较小的变量时，BP神经网络预测后的相对误差为0.004 7，平均误差为0.023 2，方差为2.708 0×10-4，如表13所示。经过对比可以说明，在剔除相关性较小的变量后，墒情的预测精度要优于未剔除相关性较小的变量的预测精度。

表13 BP神经网络结果对比Tab. 13 Comparison of BP neural network results

3 结论

本文针对影响土壤墒情变化的因素，通过运用相关性分析、ROC曲线分析、卡方分析相结合的手段得出与墒情变化的相关性较大的变量，然后通过线性回归分析与BP神经网络，来对有无剔除相关性较小变量时的墒情进行预测对比分析。

1) 经过相关性分析可以得出，影响墒情变化的相关性较大的变量为蒸发量、降水、气压、地温、日照时数和风速。

2) 经过ROC曲线分析，得出在有降水和无降水状态下的阈值，且对相关性分析得出的结果进行了进一步的验证。

3) 根据ROC曲线得出的阈值，然后通过卡方分析可以得出，在墒情较高或者较低的情况下，影响墒情变化最主要的因素是蒸发量、地温、气压、日照时数和风速。

4) 本文对比了在有无剔除与墒情变化相关性较小变量的预测分析，通过分析结果可以得出，经过剔除与墒情变化相关性较小的变量后，线性回归分析预测的标准偏差为12.888 3，BP神经网络在剔除相关性较小变量时预测值的相对误差为0.004 7，二者预测的结果均优于未剔除相关性较小变量时的预测结果。

5) 在剔除与墒情变化相关性较小的变量后，不仅可以降低预测模型的维数，其对墒情的预测值也会更加准确，为今后农场更加精准的获悉土壤墒情提供可能。