农用车辆橡胶隔振元件动力学模型研究*
高琦,邱绪云,宋裕民
(山东交通学院汽车工程学院,济南市,250357)
通讯作者:邱绪云,男,1977年生,山东临沂人,博士,教授;研究方向为车辆底盘设计与控制。E-mail: qiuxuyun@163.com
0 引言
我国农业机械化迅猛发展的过程中,农用车辆的广泛应用大大提高了农业生产和运输的效率[1]。农用车辆的使用工况相对恶劣,在作业和行驶过程中使车辆各结构部件产生剧烈振动,同时发动机产生的振动也会传递给车辆各系统及其部件,不但会降低农用车辆作业稳定性,引起结构噪声,也会影响各部件的疲劳寿命[2-3]。
橡胶隔振元件作为农用车辆动力装置、减振装置等部件间的连接元件与隔振元件,其动力学特性直接影响农用车辆的隔振与降噪性能,它具有很强的非线性粘弹力学特性,受外界因素(加载幅值、加载频率、工作周期以及温度等)的影响比较大[4]。橡胶隔振元件模型的精度是农用车辆各子系统及整车动力学仿真精度的关键影响因素之一,目前尚没有公认可接受的高精度橡胶隔振元件模型用于整车及子系统模型动态仿真。因此,建立能够准确描述橡胶隔振元件动态特性的动力学模型,对于提高农用车辆整车模型仿真精度以及准确预测复杂工况下各子系统特性对车辆隔振与降噪性能的影响具有重要意义。
目前为止,国内外学者提出了不同的动力学模型用于描述橡胶隔振元件的动态力学特性,为克服Kelvin-Voigt模型、Maxwell模型、三参数Maxwell模型、广义Maxwell模型以及Zener模型的不足,分数导数模型因模型参数相对较少、调整能力强、能反映较宽频域内加载历程对橡胶材料动态特性的影响而日益受到关注[5-10]。这类模型多为阶次不大于1的低阶分数导数模型,在预测橡胶材料的能量损耗频率相关性方面存在一定误差,建立的模型往往需要进行一定的修正和改进才能更加精确地试验结果吻合。最高阶次大于1的高阶分数导数模型更接近于描述橡胶材料物理本质[11-13],但相关研究相对较少,因此,本文基于高阶分数导数粘弹性理论建立弹性单元、摩擦单元和高阶分数导数粘弹性单元叠加的橡胶隔振元件动力学模型,提出基于广义多维学习策略和自适应调整策略的粒子群算法的粘弹性单元参数辨识方法,并推导高阶分数导数粘弹性单元的数值求解方法,为实现橡胶隔振元件在农用车辆各系统及整车动力学仿真分析中的精确表征奠定基础。
1 橡胶隔振元件动态力学试验
选取某农用车辆发动机前悬置软垫为试验对象,基于MTS831衬套试验机进行了轴向动态加载试验,如图1所示。

图1 某农用车辆发动机前悬置软垫轴向动态加载试验Fig. 1 Axial dynamic loading test for the engine front mounting cushion of an agricultural vehicle
通过分析该橡胶软垫的工作特性,先对其施加1 000 N 的预载,然后进行频率为1~50 Hz,振幅分别为0.1、0.2、0.4、1.0和2.0 mm的动态力学加载试验,得到在不同加载振幅下其动刚度与阻尼系数随加载频率的变化曲线,如图2和图3所示。

图2 不同加载幅值下橡胶软垫动刚度随频率的变化Fig. 2 Variation of dynamic stiffness of rubber cushion with frequency under different loading amplitudes
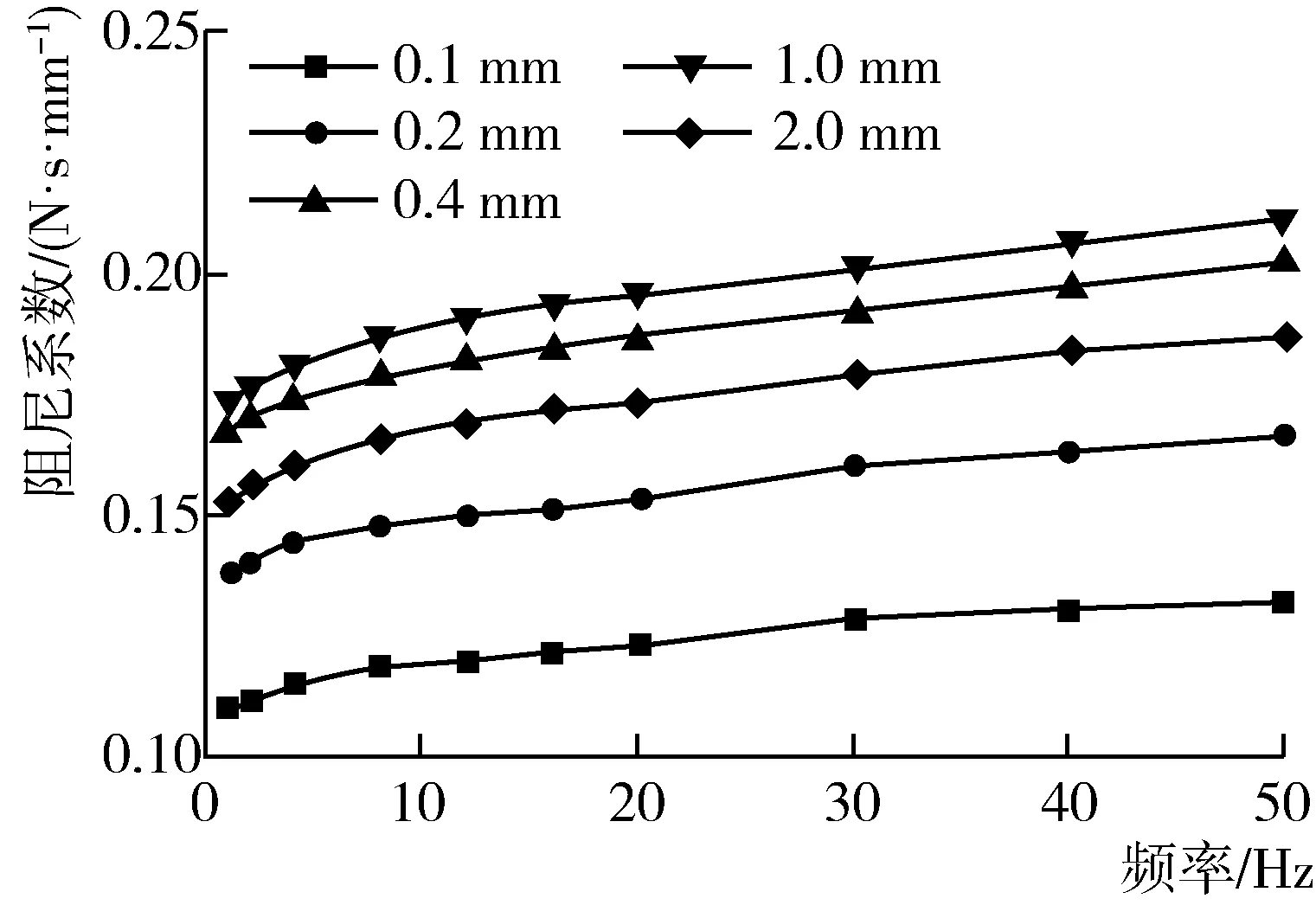
图3 不同加载幅值下橡胶软垫阻尼系数随频率的变化Fig. 3 Variation of damping coefficient of rubber cushion with frequency under different loading amplitudes
从图2和图3可以看出,在1~50 Hz频率范围内,在同一振幅下,橡胶软垫动态刚度与阻尼系数均随频率的增加而增大;在频率相同时,随着振幅的增加,橡胶软垫的动刚度逐渐下降,阻尼系数具有先增大再减小的趋势。
2 橡胶隔振元件动力学模型
所建立的橡胶隔振元件动力学模型由弹性单元、摩擦单元以及粘弹性单元叠加组成,如图4所示。Fe、Ff、Fv和F依次为橡胶隔振元件模型的弹性力、摩擦力、粘弹力和总响应力,N。
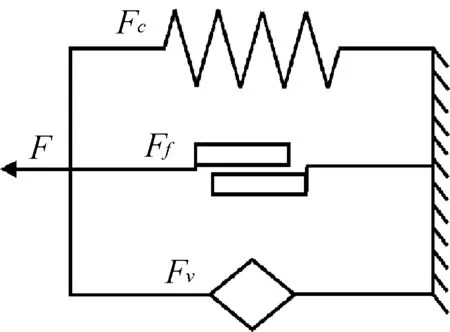
图4 橡胶隔振元件动力学模型示意图Fig. 4 Dynamic model of rubber vibration isolation component
2.1 弹性单元
弹性单元用来描述橡胶隔振元件的静态主刚度。橡胶隔振元件的弹性特性在线变形范围内符合胡克定律,当变形量超过一定范围后,其弹性特性呈现出明显的非线性。弹性单元中,弹性力与加载位移的关系可使用弹簧模型来描述。文献[14]指出,与正切弹簧模型和结构弹性单元模型相比,幂次多项式模型可以灵活而有效地描述弹性力与加载位移之间的线性或非线性关系。因此,选用幂次多项式模型描述橡胶隔振元件的弹性特性。
Fe=a0+a1x+a2x2+a3x3+…+anxn
(1)
式中:Fe——弹性力,N;
x——加载位移,mm;
a0,a1,a2,a3,…,an——幂次项的系数。
在振幅为x0的简谐激励下,弹性力的幅值
(2)
2.2 摩擦单元
摩擦单元中,摩擦力与加载位移的关系[13]
(3)
式中:Ff——摩擦力,N;
Ffmax——最大摩擦力,N;
x2——Ff从0开始,逐渐增大至Ffmax/2时的位移,mm;
xs——摩擦力与位移变化曲线上的起始点或反向点的位移,mm;
Ffs——摩擦力与位移变化曲线上位移为xs的摩擦力,N;
(xs,Ffs)——摩擦力与位移变化曲线上的状态参考点,此处取(0,0)。
在振幅为x0的简谐激励下,摩擦力的幅值
(4)
一个加载循环损耗的能量为
(5)
其中u0=Ff0/Ffmax。
2.3 粘弹性单元
选用分数阶Kelvin-Voigt模型与分数阶Maxwell模型并联的高阶分数导数粘弹性模型描述橡胶材料的粘弹性特性[13],如图5所示。图5中k1和c1分别为分数阶Kelvin-Voigt模型中弹簧的弹性模量和黏壶的粘性系数,k2和c2分别为分数阶Maxwell模型中弹簧的弹性模量和黏壶的粘性系数。k1和k2用于反映材料的弹性模量,c1和c2用于反映材料的粘性。
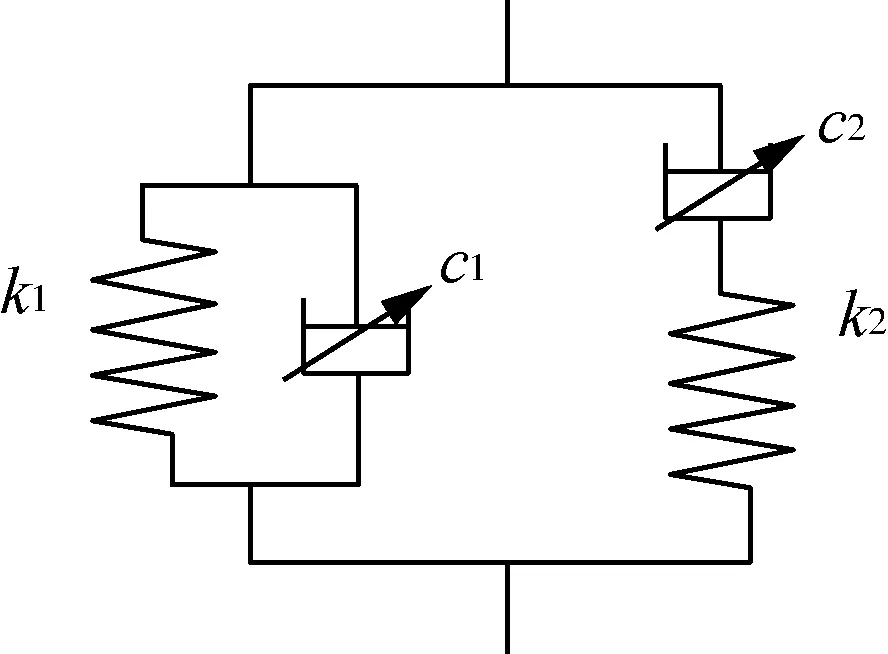
图5 高阶分数导数粘弹性模型示意图Fig. 5 High-order fractional derivative viscoelastic model
根据图5所示模型,可得粘弹力与位移的关系
λ1λ2x(t)
(6)
其中λ1=k1/c1,λ2=k2/c2。
式中:Fv(t)——粘弹力,N;
x(t)——加载位移,mm;
α、β、γ——取值范围(0,1)的分数导数阶数,其中α+γ的最高阶数为2。
对式(6)进行傅里叶变换,得该分数导数粘弹力模型的复刚度
(7)
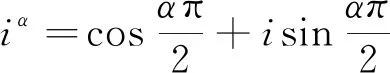
(8)
(9)
一个加载循环损耗的能量为
(10)
2.4 橡胶隔振元件动力学模型
将弹性单元、摩擦单元与分数导数粘弹性单元叠加,得到橡胶隔振元件动力学模型的总响应力与加载位移的关系
F(x)=Fe(x)+Ff(x)+Fv(x)
(11)
式中:F(x)——橡胶隔振元件动力学模型的总响应力,N;
Fe(x)——弹性力,N;
Ff(x)——摩擦力,N;
Fv(x)——粘弹力,N。
在x=x0sin(ωt)的简谐激励下,总响应力振幅
(12)
橡胶隔振元件模型的动刚度
(13)
橡胶隔振元件模型的阻尼系数
(14)
3 橡胶隔振元件动力学模型参数辨识
由于建立的橡胶隔振元件动力学模型,各单元之间满足叠加原理,因此,模型参数的获取可依次通过辨识摩擦单元、弹性单元以及粘弹性单元的参数实现。
3.1 摩擦单元参数辨识
由于加载速度较低时,粘弹性单元对橡胶衬套的响应特性影响较小,为保证摩擦力能够得到充分体现,采用低频率、大振幅的动态加载工况对摩擦单元参数进行辨识,摩擦单元参数辨识示意图如图6所示。
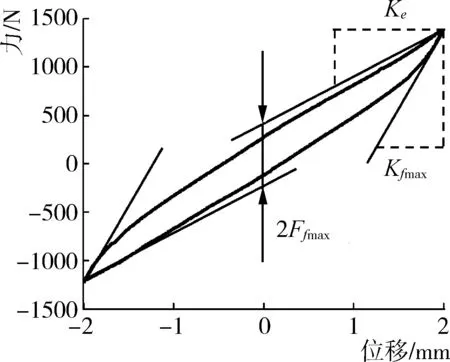
图6 低频加载工况下摩擦单元参数辨识示意图Fig. 6 Parameter identification of friction element under low frequency loading
图6中,加载位移达到最大时,摩擦力稳定达到最大,此时曲线上端面接近极限位置处的斜率可近似表示该元件在此段位移的弹性刚度Ke。延长接近极限位置的上、下两条切线,摩擦力模型中最大摩擦力Ffmax的值即为两条切线间的垂直距离的1/2。取曲线下端面最大斜率的值Kmax,由式(15)可求得,摩擦单元中的x2[15]。
(15)
3.2 弹性单元参数辨识
弹性分力属于橡胶隔振元件的静态特性,也可通过低频率、大振幅的动态加载工况对弹性单元的参数进行辨识。为去除摩擦分力的影响,辨识出摩擦单元参数后,除去迟滞环曲线中摩擦分力分布,可得到弹性单元的刚度曲线,使用最小二乘法对弹性单元中多项式的系数进行拟合,可得多项次幂和幂次项的系数。
3.3 粘弹性单元参数的辨识
橡胶隔振元件动态特性的频率相关性主要通过粘弹性单元体现,为尽量减小摩擦力的影响,需通过小振幅加载工况获取。为充分体现其在不同频率工况下的粘弹性特性,选取振幅为0.1 mm,频率别1、2、4、8、12、16、20、30、40和50 Hz共10个正弦加载试验工况进行粘弹性单元k1,c1,k2,c2,α,β和γ共7个参数的辨识。
粘弹性单元参数辨识实质上是一个最优参数估计问题,为使识别结果尽可能接近试验测量结果,通过建立橡胶元件模型计算的动态响应与试验得到元件的动态响应误差最小的优化函数来实现。此处基于橡胶隔振元件动刚度和阻尼系数误差建立优化目标函数
(16)
式中:M——辨识工况的总个数;
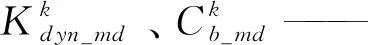
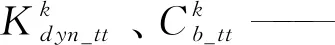
由于粘弹性单元中包含高阶分数导数项,具有复杂的非线性,且需要辨识的参数较多,传统的数学寻优算法对非线性系统参数进行辨识时,要求目标函数连续可导,且搜寻最优解时易陷入局部最优。粒子群优化(Particle Swarm Optimization,PSO)算法作为一种非解析仿生智能寻优算法,对非线性系统参数辨识具有较好的应用效果。为了提升传统的PSO算法收敛速度较慢,降低陷入局部极值点的可能性,本文选取一种基于广义多维学习策略和自适应调整策略的PSO算法[16]对粘弹性单元的参数进行辨识。
以式(16)所示目标函数作为适应度函数,算法中更新粒子的方法如式(17)所示。
i=1,2,3,…,n;j=1,2,3,…,d
(17)
式中:t——当前迭代次数;
zi,j(t)——第t代中粒子适应度值递减顺序排序后第i(1≤i≤n)个粒子Pi的位置向量的第j(1≤j≤d)维;
vi,j(t)——粒子Pi的速度向量的第j维;
bi(t)——一个随机产生的概率;
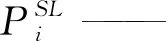
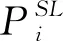
(18)
式中:d——粒子的搜索维数;
n——群中的粒子数;
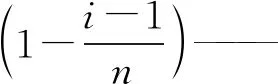
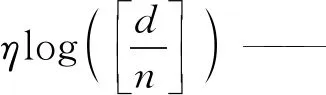
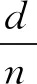
粒子Pi根据式(19)更新自己的每一维速度
(19)
式中:ωEt——动态调整的惯性权重;
zg,j(t)——粒子Pi的位置向量第j维的学习对象Pg的位置向量第j维;
κ——社会影响系数,κ取值比较大时,可能导致过早收敛到平均行为的现象;
r1、r2——广义多维学习部分和社会学习部分的权重,取值为0~1之间均匀分布的随机数。
(20)
式中:ni——落入每个小区间的粒子数。
为保证粘弹性单元参数识别的准确性,提高模型的预测精度,参数识别过程中,需使模型计算的每个频率工况下动刚度和阻尼系数,与试验值均不能有较大误差。通常认为模型的计算精度在90%以上,可满足工程应用要求,为此,建立约束条件
(21)
参数识别过程中算法的收敛性准则为
(22)
式中:σfobj——所有粒子适应值的标准差;
μfobj——所有粒子适应值的平均值。
该判据可以避免在fobj的全局最优值附近出现小的波动。否则,当迭代次数达到最大迭代次数Gmax时,优化过程终止。
经多次调试,算法各参数设置如下:粒子维数d为7,位置向量x=(k1,k2,c1,c2,α,β,γ),各维搜索空间下限zmin=(0,0,0,0,0,0,0),上限zmax=(103,103,103,103,1,1,1);群中的粒子数n取30,广义多维学习部分权重r1和社会学习部分权重r2为0~1之间均匀分布的随机数,最大迭代次数Gmax取100。粘弹性单元参数辨识的流程如图7所示。
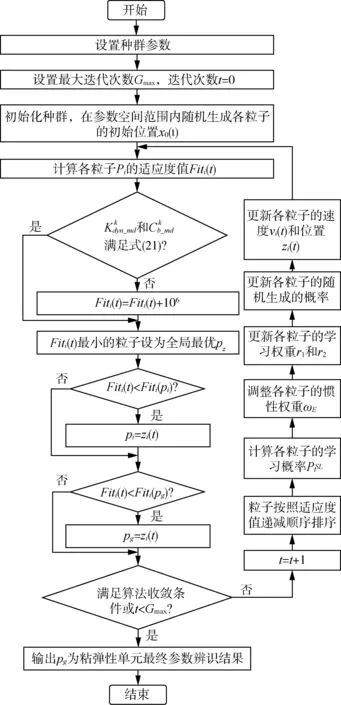
图7 粘弹性单元参数辨识流程图Fig. 7 Flow chart of identification for viscoelastic element parameters
3.4 橡胶隔振元件模型参数辨识结果与验证
橡胶隔振元件模型各单元参数辨识结果如表1所示。各单元参数辨识完成后,基于橡胶隔振元件动力学模型进行了正弦激励动态仿真计算。将计算结果与试验结果进行对比,如图8和图9所示。
从图8和图9可以看出,模型仿真计算的橡胶隔振件的动刚度与阻尼系数的频率响应特性与幅值响应特性均与试验结果基本一致。由于摩擦单元损耗的能量不受频率影响,使在激励频率较小时,模型仿真计算出的橡胶隔振能量损耗不为零。由此可见,所建模型能够准确地描述橡胶隔振元件动态特性的分布特征。
在振幅0.1~2 mm、频率1~50 Hz范围内,对模型仿真计算结果与试验结果进行统计,得到该模型在不同振幅工况下,动刚度的平均误差和最大误差分别为3.08%和4.52%,阻尼系数的平均误差和最大误差分别为4.58%和5.79%,说明建立的模型在不同振幅和频率下均有较高的精度。
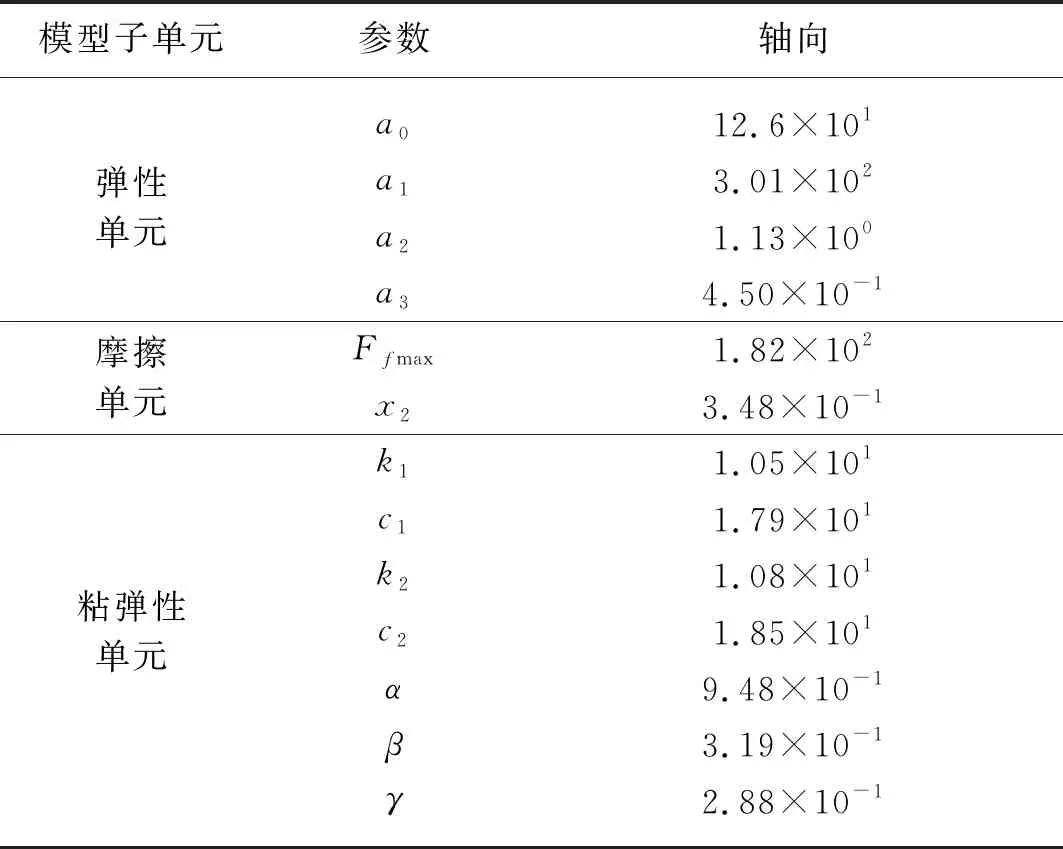
表1 橡胶隔振元件模型各单元参数辨识结果Tab. 1 Identification results of element parameters of
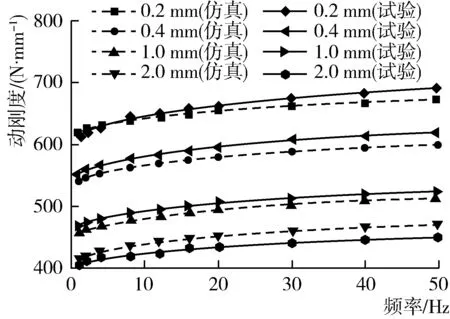
图8 橡胶隔振元件动刚度模型计算值与试验值对比Fig. 8 Comparison of dynamic stiffness between model calculation value and test value of rubber vibration isolation element
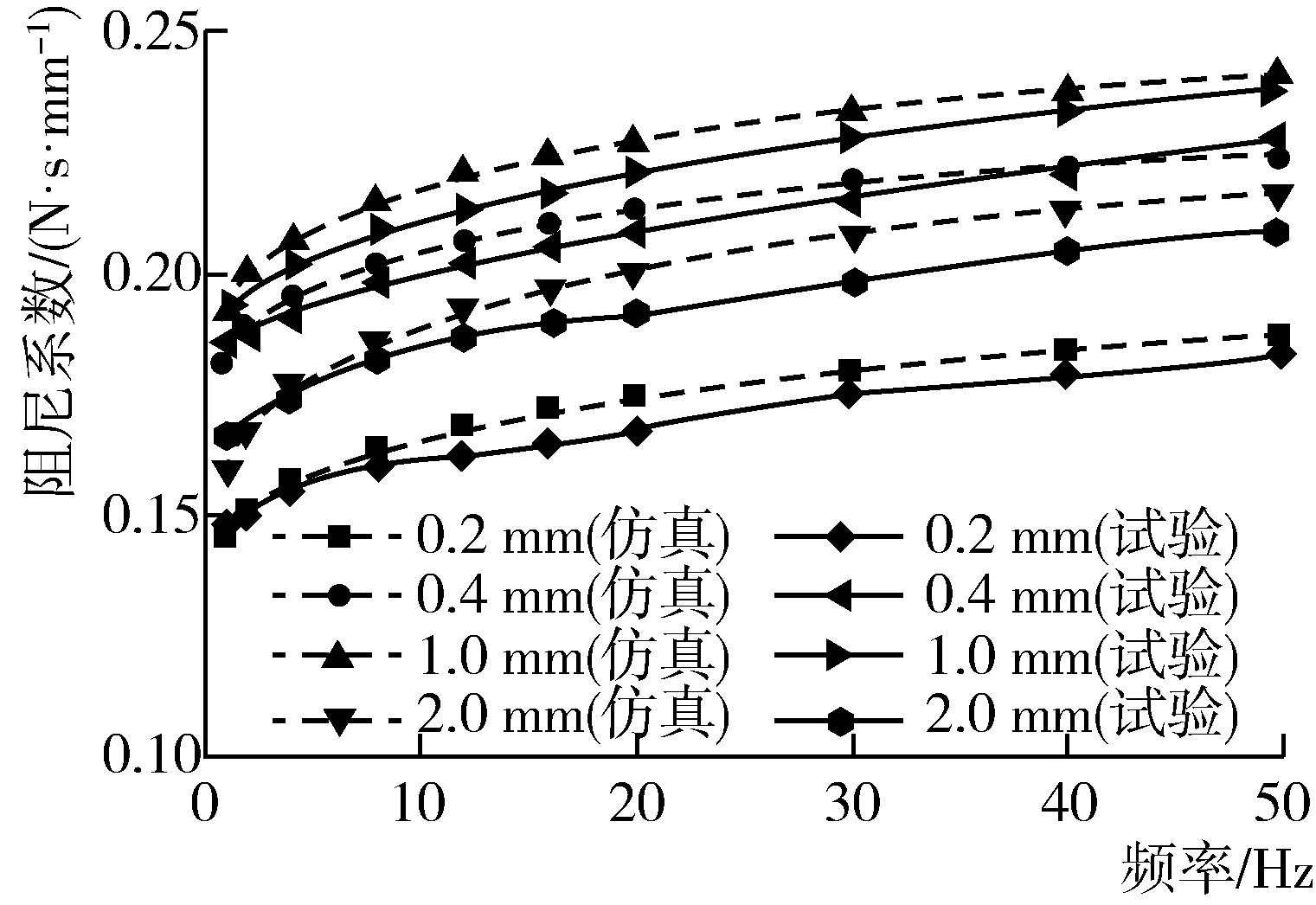
图9 橡胶隔振元件阻尼系数模型计算值与试验值对比Fig. 9 Comparison of damping coefficients between model calculation value and test value of rubber vibration isolation element
4 橡胶隔振元件动力学模型数值求解
为了将建立的橡胶隔振元件动力学模型应用于农用车辆动力学建模与分析中,对橡胶隔振元件模型的数值求解方法进行推导。
4.1 高阶分数导数粘弹性单元数值求解
根据整数阶微积分理论,可导函数f(t)对时间t的整数阶导数可由各阶向左做差商的极限定义,当m取自然数时,可推导f(t)的m阶导数为
(23)
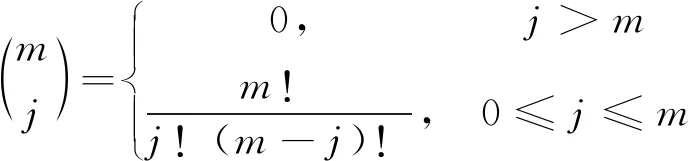
式中: Δt——时间变量t在取值范围内微小增量。
将式(23)整数阶导数的定义推广到任意阶,即将式(23)中的整数m用任意实数ε取代,并引入Gamma函数,可得到Grunwald-Letnikov形式的分数阶导数
f(t-jΔt),ε>0
(24)
式中: Γ(·)——Gamma函数,Γ(n)=(n-1)!。
设函数f(t)定义在区间[0,T](T为大于0的任意实数)上,用分数代替Δt,即Δt=t/N(N为自然数),则式(24)可以写成
(25)
由于
(26)
因此,可得到
(27)
零初始条件下,当N取一极大值时,可进一步得到分数阶导数的数值计算公式
(28)
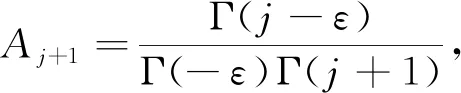
(29)
由式(6)可知,橡胶隔振元件模型中粘弹性单元的微分方程含多个分数导数项。一个微分方程中含有多个导数项的方程进行数值计算,根据分数导数运算的可加性,可先把方程降阶为多个方程组成的方程组,使每个方程中含有一个导数项,再进行分数阶计算[17]。
考虑如下形式的分数阶微分方程
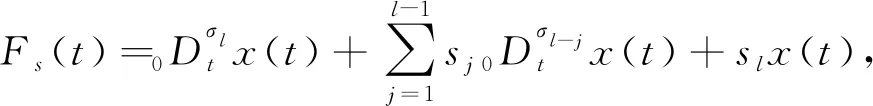
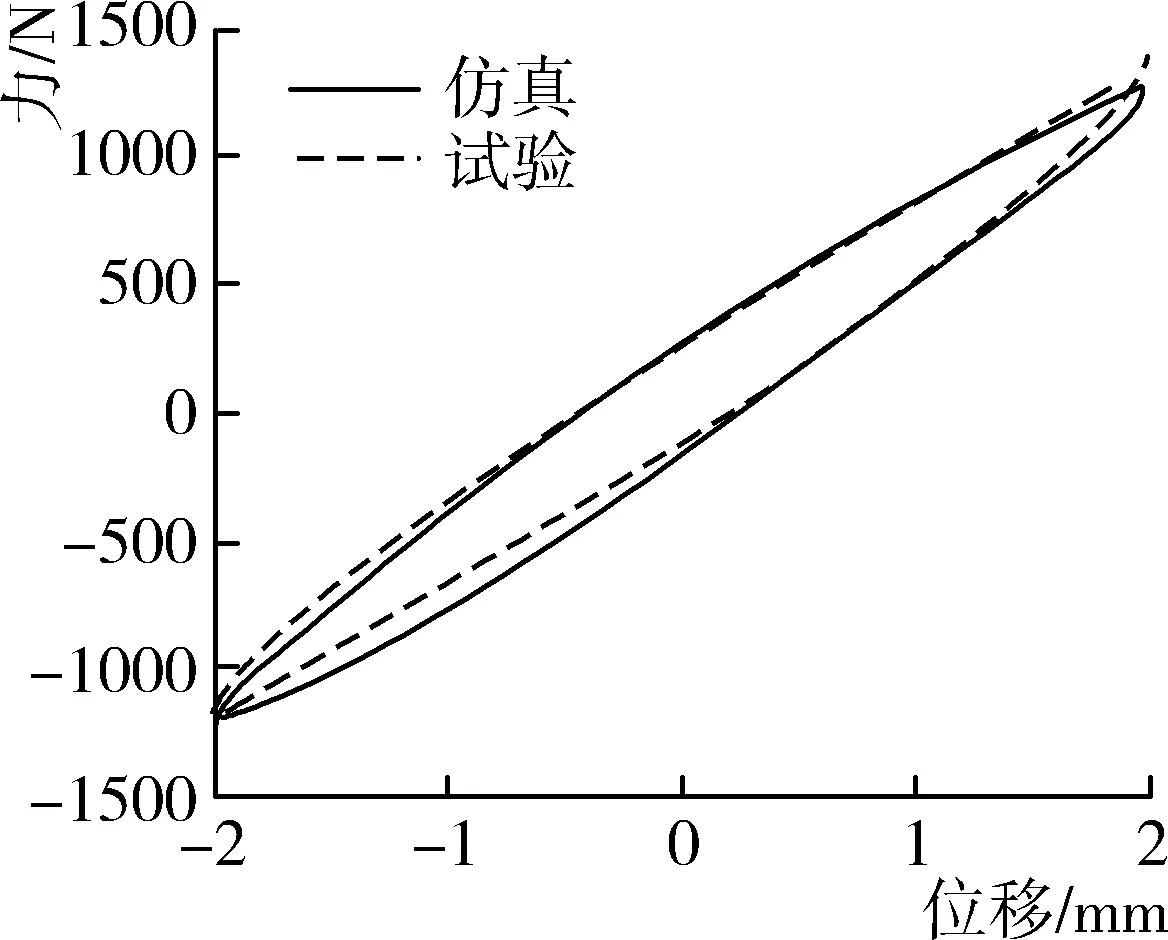
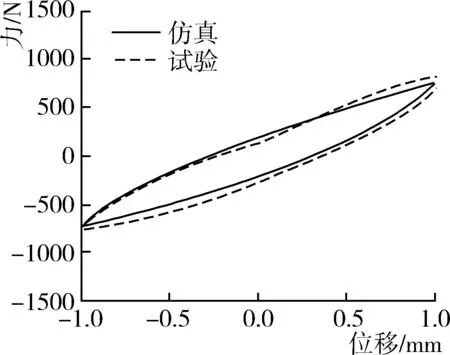
0 (30) 式中:x(t)——位移,mm; Fs(t)——响应力,N; sj——分数阶导数项的系数; sl——一次项的系数; σl、σl-1——分数阶导数的阶数,σl和σl-1为大于0的实数,且σl>σl-1。 式中:θh——取值在(0,1]区间内的实数。 根据分数导数运算的可加性,对式(30)进行降阶处理,设 (31) 用y1替换x(t),则式(31)可变形为 (32) (33) 以橡胶隔振元件的加载位移作为输入时,可先将位移的各导数项按上述方法进行降阶处理为式(32)所示的形式,并根据迭代公式(29)对方程组各项进行数值计算,得到各位移项当前时刻的值;然后再将粘弹力的各项按上述方法进行降阶处理,再结合迭代公式(29),求解出当前时刻粘弹力值。 在每一时刻的加载位移下,根据4.1节推导的数值求解方法求取粘弹力,再根据式(1)与式(3)分别求取弹性力与摩擦力,最后将上述各单元力代入式(11),求得橡胶隔振元件模型的总响应力。 分别取频率1 Hz、振幅2 mm和频率50 Hz、振幅1 mm两种正弦信号作为位移输入,进行数值求解得到橡胶隔振元件的总响应力,并与试验结果进行对比,如图10和图11所示。 图10 1 Hz、2 mm工况下仿真与试验力—位移曲线Fig. 10 Simulation and test force-displacement curves under 1 Hz and 2 mm working condition 图11 50 Hz、1 mm工况下仿真与试验力—位移曲线Fig. 11 Simulation and test force-displacement curves under 50 Hz and 1 mm working condition 从图10和图11可以看出,在不同频率工况下,数值求解得到橡胶隔振元件的力—位移曲线与试验测得的力—位移曲线具有较好的一致性。 1) 以某农用车辆发动机前悬置软垫为载体,通过动态加载试验对其轴向频率响应特性和幅值响应特性进行了研究,建立了弹性单元、摩擦单元和高阶分数导数粘弹性单元叠加的橡胶隔振元件动力学模型。 2) 运用基于广义多维学习策略和自适应调整策略的粒子群算法进行了粘弹性单元参数辨识,结合试验结果,辨识得到了模型参数。经试验验证,在振幅0.1~2 mm、频率1~50 Hz范围内,所建模型仿真计算与试验得到动刚度的平均误差和最大误差分别为3.08%和4.52%,阻尼系数的平均误差和最大误差分别为4.58%和5.79%,说明建立的模型能够精确地预测橡胶隔振元件的动态响应特性,以期为复杂工况下准确预测农用车辆系统动态响应特性奠定基础。 3) 推导了高阶分数导数粘弹性模型的数值求解方法,并应用于橡胶隔振元件动力学模型的数值求解,通过与试验结果进行对比,验证了该方法的正确性与有效性。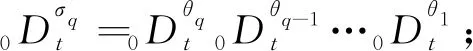
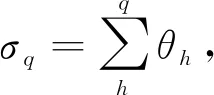
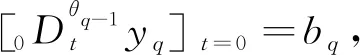
4.2 数值求解结果验证
5 结论

