基于微型燃气轮机发电的混合动力系统小信号稳定性分析及前馈补偿控制

李鸿扬，温旭辉，王又珑

(1. 中国科学院电力电子与电气驱动重点实验室， 中国科学院电工研究所， 北京 100190;2. 中国科学院大学， 北京 100049)

1 引言

由燃气轮机、发电机及整流器、电力推进负载等组成的混合动力系统如图 1所示。由于各个模块独立设计，对系统其他模块的参数匹配和控制结构、参数对系统稳定性的影响考虑不充分，故在各个模块集成后，可能会出现系统不稳定现象[1-3]。例如，在整流器设计时，通常以电阻为负载进行控制结构和参数设计，但在混合动力系统中整流器的负载多呈现负阻抗特性的恒功率负载，这将导致在集成后，由于模块之间的相互作用产生稳定性问题。

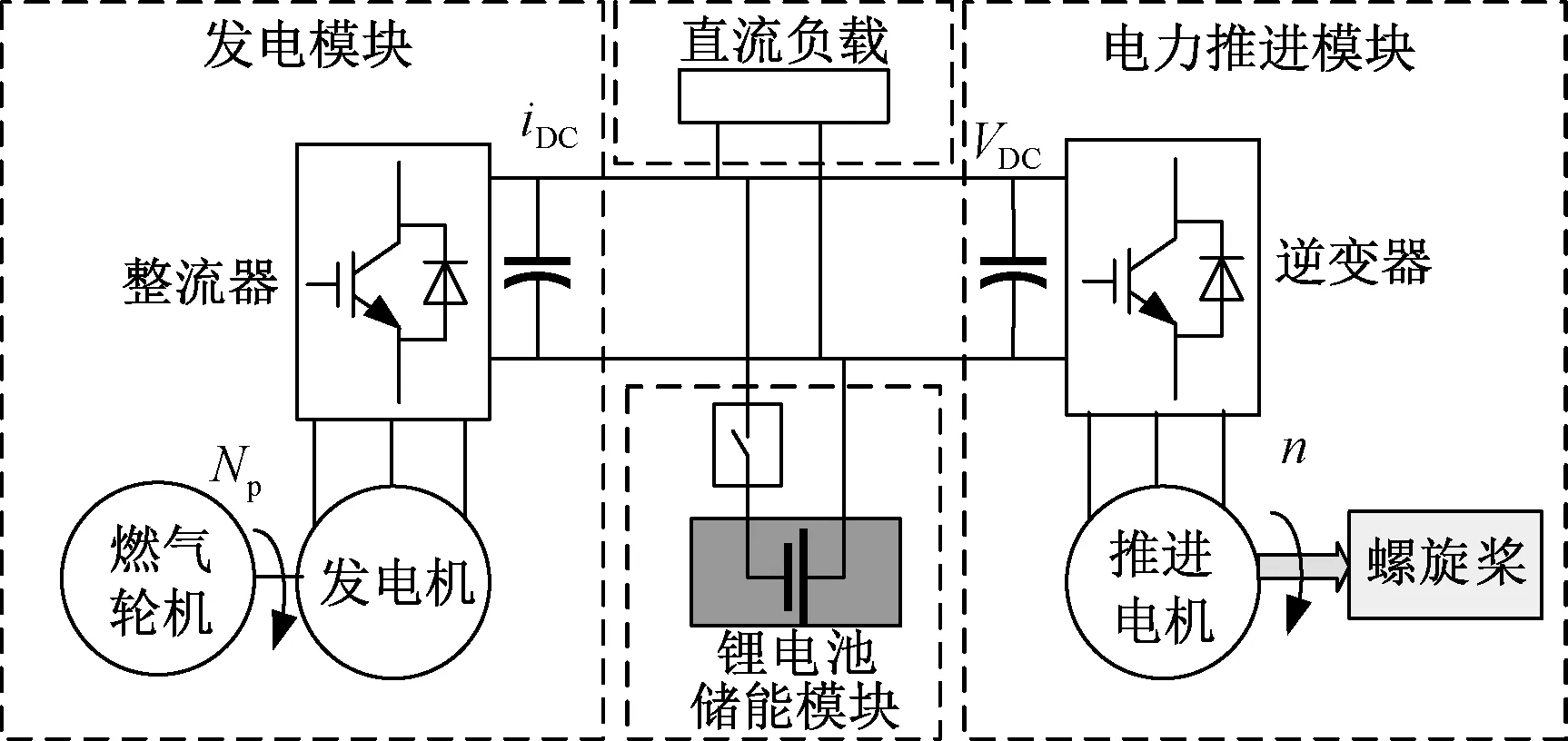
图1 系统结构图

当前混合动力发电系统的小信号稳定性研究多关注于电气端口，如直流母线及多装置并联端口，而对于机械端口少有研究[4-8]。例如，在混合动力系统中的燃气轮机外特性也具有很强的非线性特征，且具有转矩响应慢及惯量小的特点，当其负载为恒压控制的发电机及整流器时，整流器及发电机对于前级模块(燃气轮机)而言为恒功率负载，使得小信号稳定性问题突出。

小信号稳定性问题是燃气轮机发电系统研究的重点和难点之一。一定程度上可以借鉴电力系统小信号阻抗稳定性分析方法进行研究。电力系统中各个变换装置在运行时，由于装置之间的相互影响，会出现不稳定现象。目前，应用最广泛的电力系统小信号稳定性分析方法是在1976 年由Middlebrook 等提出的阻抗分析法[2]。这种方法给出了满足小信号稳定性源变换器的输出阻抗和负载变换器的输入导纳之间的相互关系[2, 3]。在阻抗分析方法的基础之上，许多学者提出了不同的小信号稳定性判据以及相关的输入/输出阻抗设计要求，这其中也包括了后续广泛采用的阻抗禁止区方法[9-13]。这些方法都为系统提供了充分不必要的稳定条件，但均存在一些缺点，例如Middlebrook判据、(Opposing Argument, OA)判据、增益裕度和相位裕度(Gain Margin and Phase Margin, GMPM)判据过于保守，而(Energy Systems Analysis Consortium, ESAC)判据、最大峰值判据(Maximum Peak Criteria，MPC)判据又过于复杂，很难通过Bode图进行量化分析。

为了得到适用于微型燃气轮机发电系统小信号稳定性分析的模型，本文分析和比较了目前常用的阻抗稳定分析判据，最后选取保守性较小的MPC标准作为微型燃气轮机发电系统的稳定性判据，并对MPC判据做了改进，基于MPC标准获得输入/输出阻抗的禁止区域，进行了小信号分析。最后，针对系统小信号不稳定问题，提出了一种前馈补偿法，以提升系统小信号稳定性，解决燃气轮机带发电机整流器负载时的小信号不稳定问题。

2 小信号稳定性判据

2.1 小信号稳定性判据

大多数直流电源系统可以等效为线性源变换器系统和线性负载变换器系统，如图 2所示。其中，vs和Zs分别为线性源变换器模型的戴维南等效电压和阻抗，而vl和Zl(=1/Yl)分别为线性负载变换器模型的戴维南等效电压和阻抗，is和il分别为流入两个转换器的电流。

图2 两级直流电源系统的阻抗模型

从图 2可以看出：

(1)

若最小环路增益Tm=Zs/Yl满足奈奎斯特稳定判据，则图2的互连系统是稳定的。

为了确保集成系统的稳定性和性能，通常针对源变换器的给定输出阻抗规定负载阻抗规范。负载阻抗规范通常是根据禁止区域生成的，基于禁区提出的几种稳定性判据包括Middlebrook判据， GMPM判据， ESAC判据，OA判据[9]和MPC[13]，以上判据在s平面上定义了如图 3所示的各种禁区。

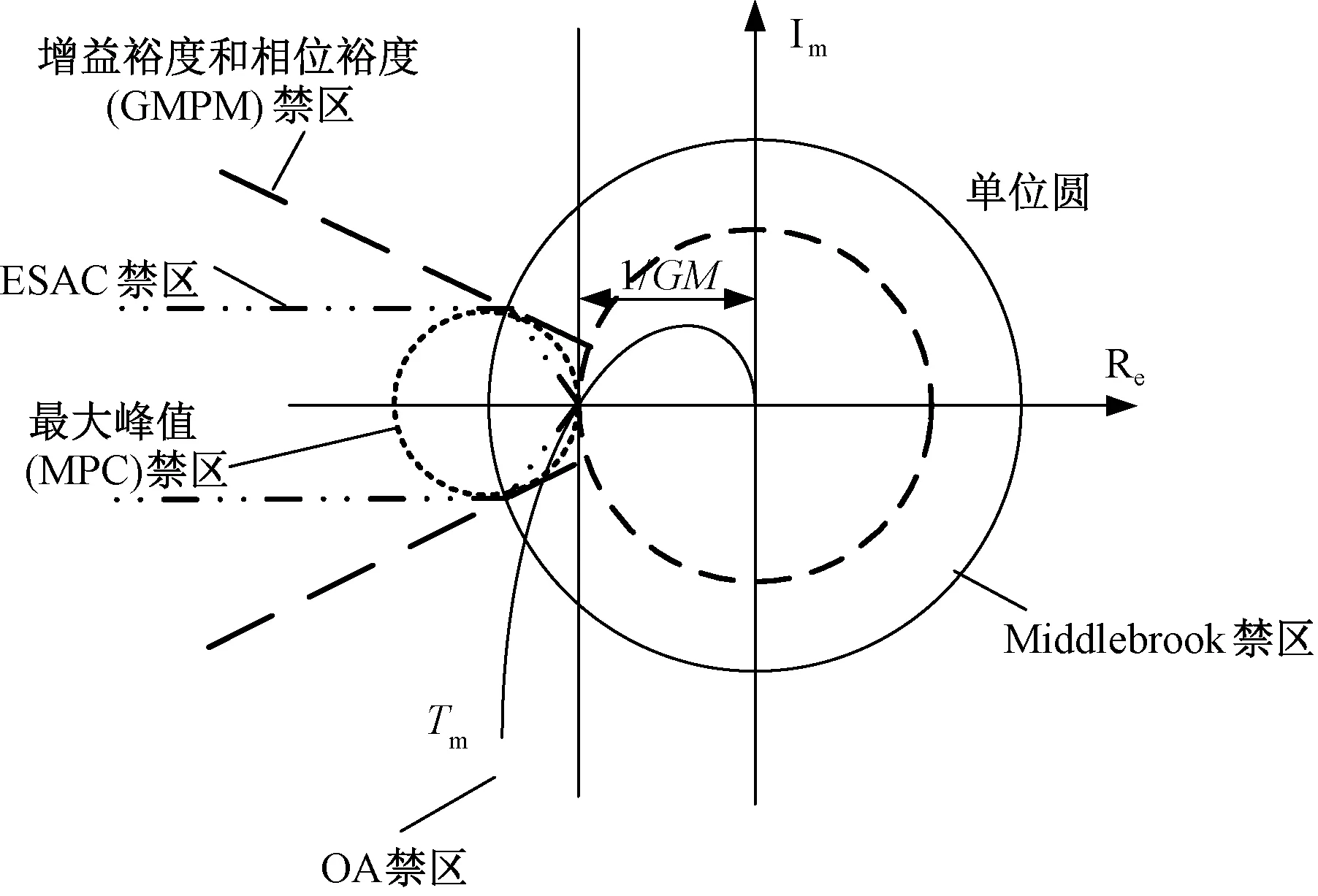
图3 文献中已有的阻抗比判据

与其他准则相比，MPC准则的禁区在复平面中占用的空间要少得多，并且保持相同甚至更好的鲁棒性。但是MPC判据只能保证系统的稳定裕度并不能保证系统的稳定性，还需使用奈奎斯特判据判断系统稳定性，给分析带来较大不便。

2.2 一种改进的MPC判据的阻抗比禁区

为解决上述问题，本文提出了改进的阻抗比禁区，如图 4(a)所示。在MPC禁区的基础上，加入禁区左侧实轴作为新的禁区。该禁区包含奈奎斯特稳定判据，既能保证系统稳定裕度，也可以保证系统稳定性。

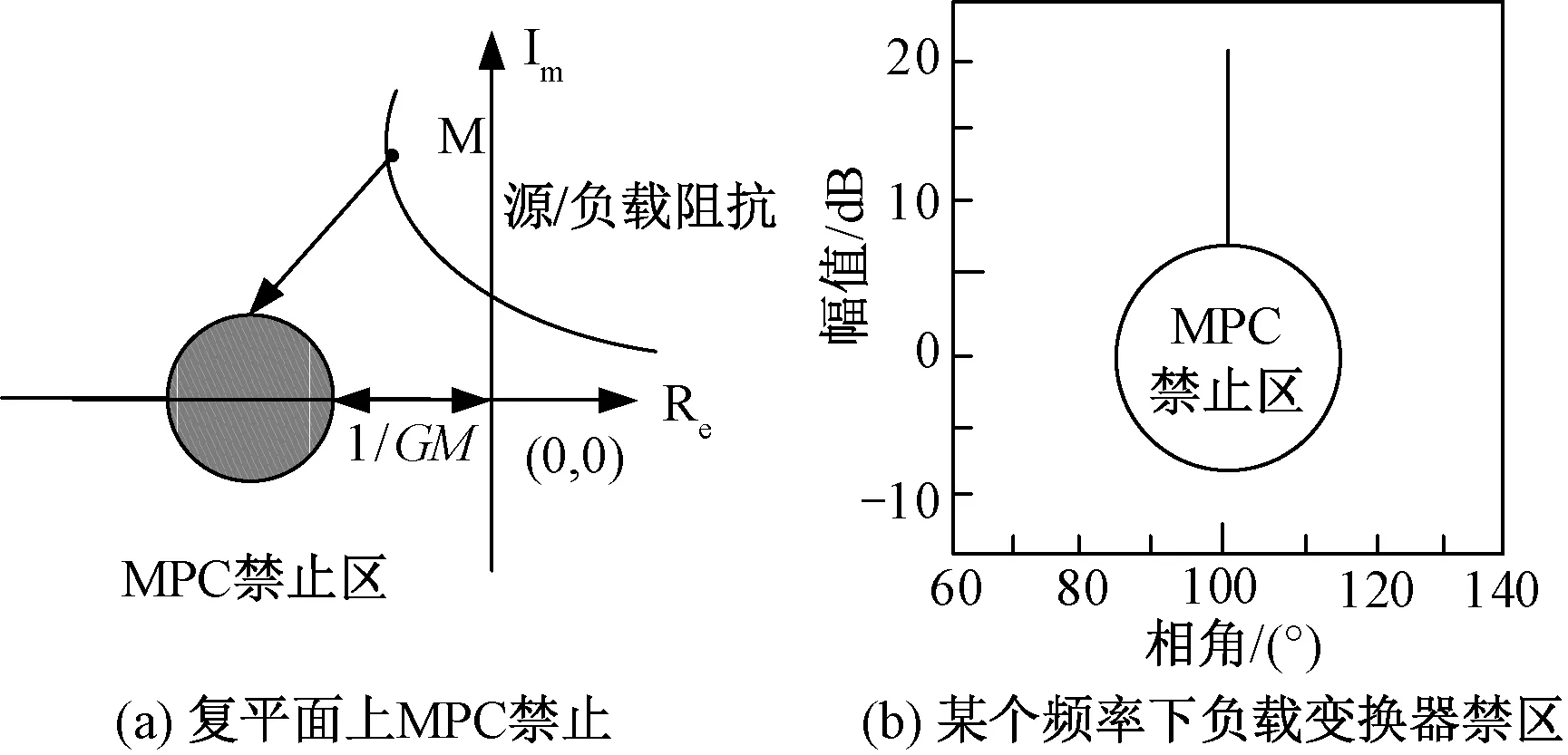
图4 改进的MPC禁止区

在已知源变换器的输出阻抗时，根据MPC标准，通过在某个频率(以M点为例)计算确定负载变换器的输入导纳在相平面中的禁止区域[9]，如图4(b)所示。以整流器为源变换器、逆变器为负载变换器为例，其参数见表1，通过源变换器的输出阻抗在全频率段计算禁止区域，可以得到的负载变换器输入阻抗禁止区域，如图5所示。文中采用的幅值裕度和相角裕度分别为3 dB和60°。

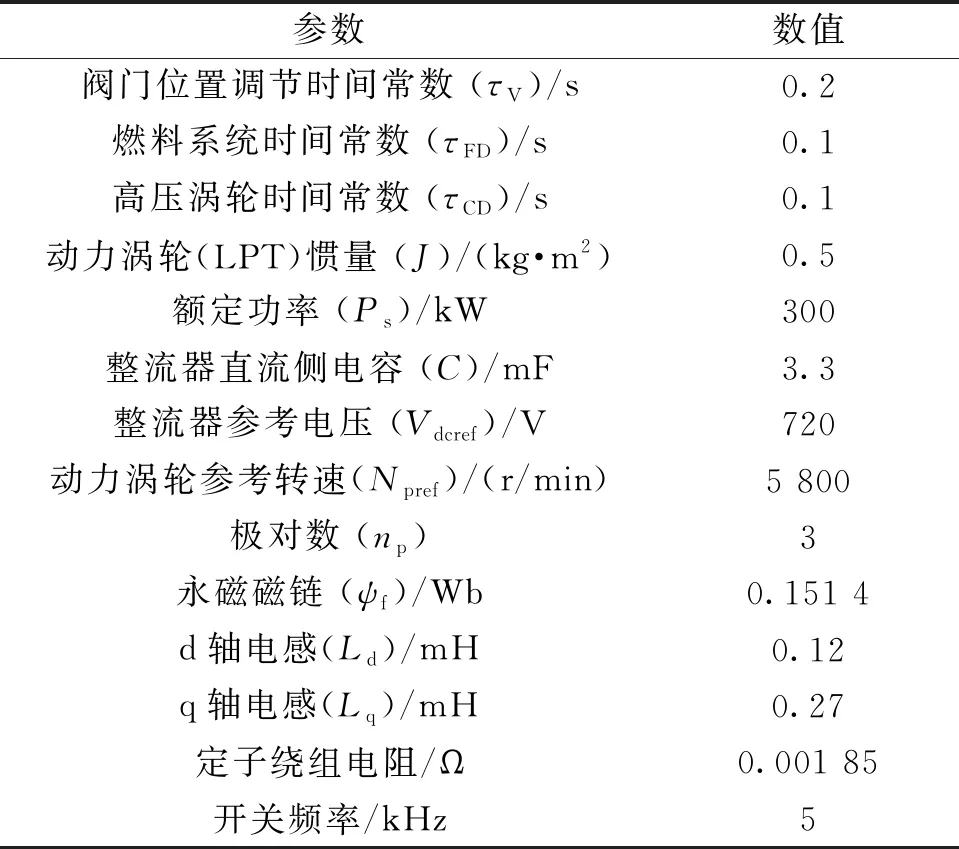
表1 系统参数

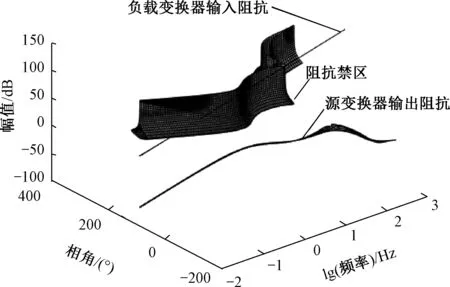
图5 源输出阻抗在s平面投影及根据源阻抗得到的阻抗禁止区域三维图

3 小信号阻抗模型

3.1 分轴燃气轮机小信号模型

分轴燃气轮机结构如图 6所示，由压气机、燃烧室、高压涡轮、动力涡轮、回热器以及换热器组成[14-16]。压气机将由吸入的空气压缩成高压气体，送入燃烧室与燃料混合后燃烧带动燃气涡轮旋转，燃气涡轮一部分能量为压缩机提供动力，其余能量通过高压、高温燃气进入动力涡轮，通过变速齿轮带动发电机工作[17-19]。

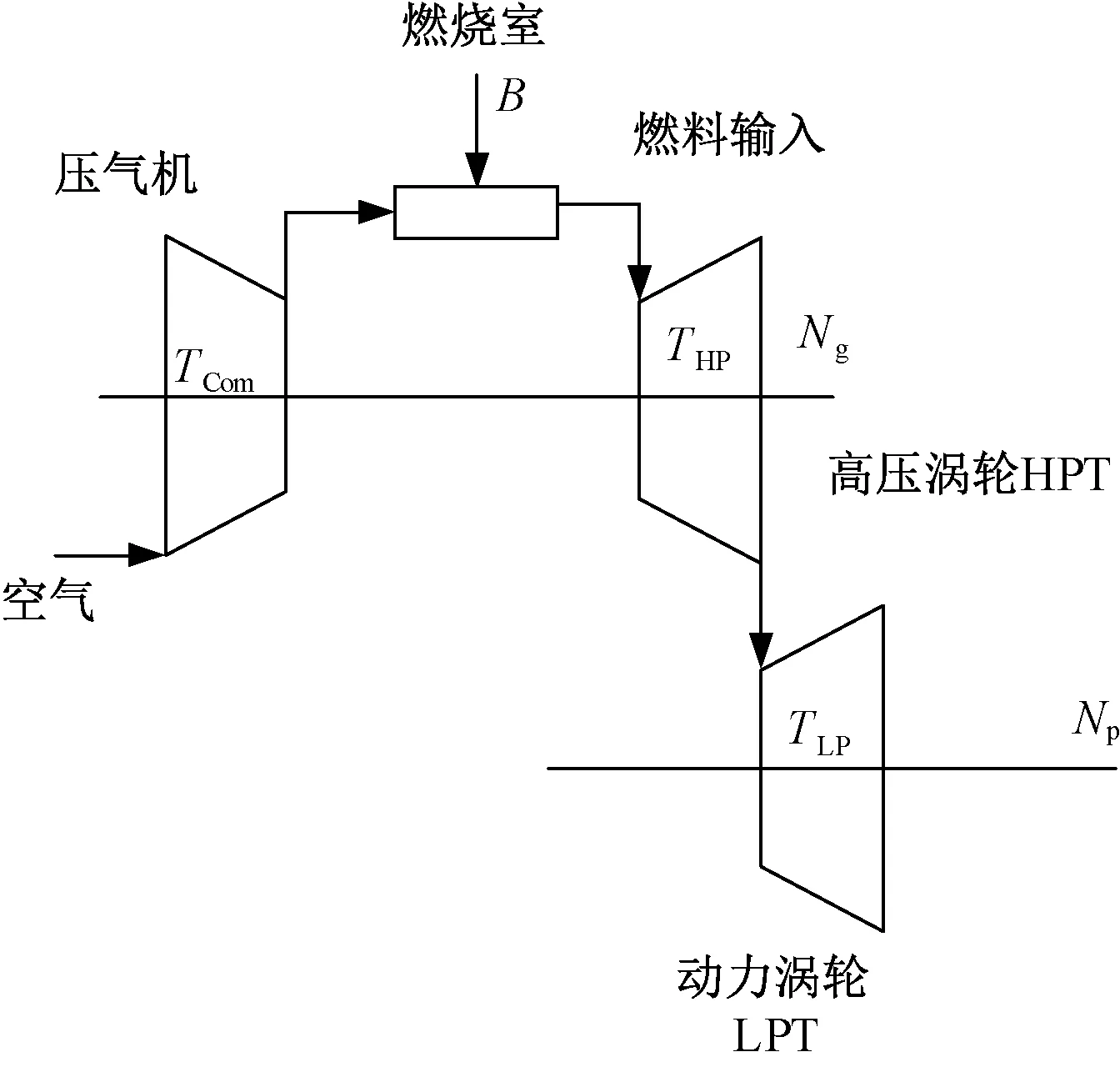
图6 分轴燃气轮机结构

Luca Bozzi提供了适用于发电厂和分布式发电应用的动态研究的双轴燃气轮机的简化数学模型，其频率依赖性低，在高压涡轮50%～110%额定转速及动力涡轮15%～110%额定转速的工况有较高的仿真精度[20]。本文以此模型为基础，改进了其控制结构，忽略了对转速控制影响较小的温度控制模块，提出了适用于双轴燃气轮机用于发电系统仿真分析的模型。

在研究燃气轮机-发电机组系统外特性时，本文只关注燃气轮机的机械特性，即动力涡轮转速动态响应。因此，可以对燃气轮机内部特性及动态过程进行简化，便于分析燃气轮机机械特性及发电机组在负载变化时的动态响应。

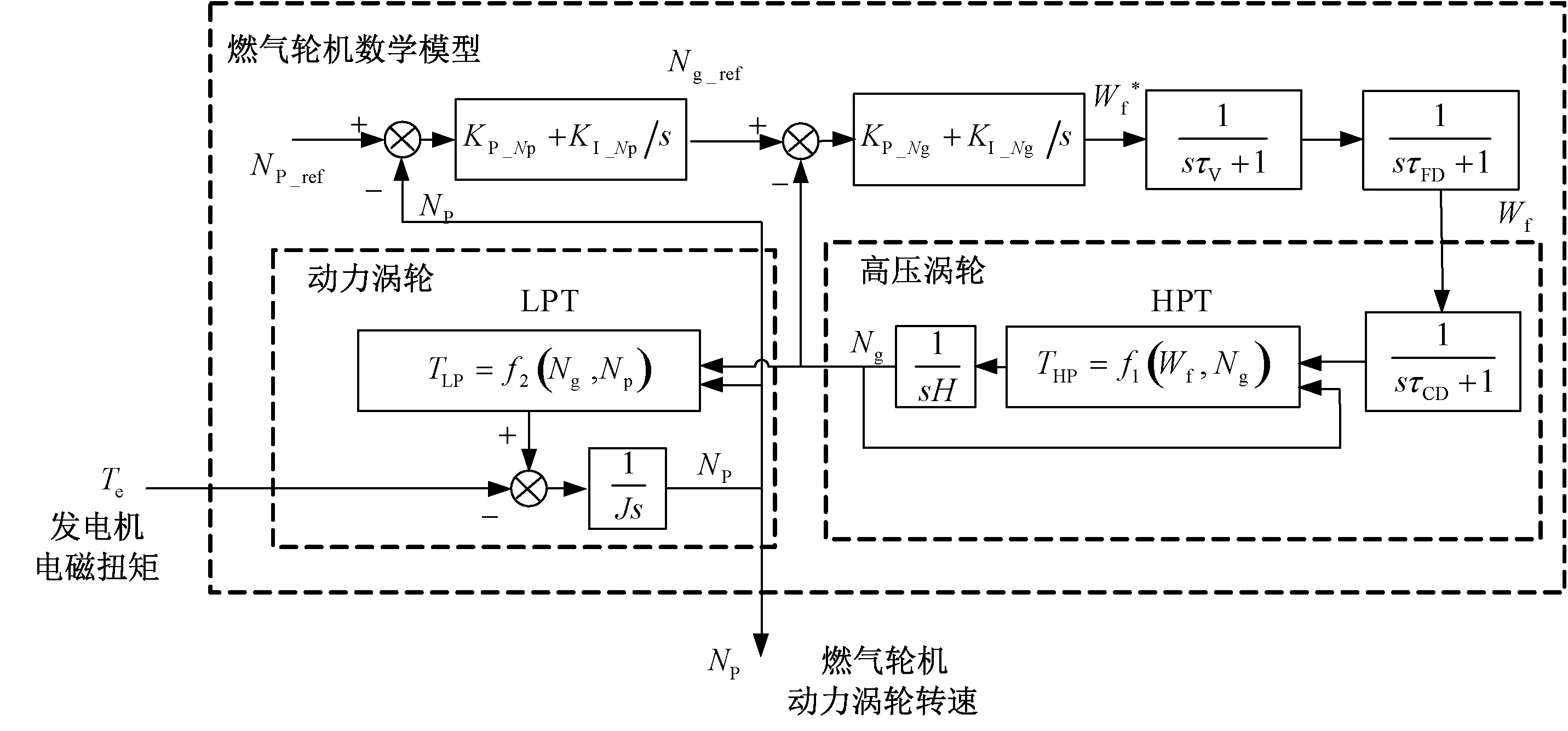
图7 双轴燃气轮机控制回路

高压涡轮及控制系统如图7所示，其中，Ng为高压涡轮转速，NP为动力涡轮转速，Wf为燃油流量指令，τV为燃油阀门时间常数，τFD为燃烧室时间常数，τCD为高压涡轮时间常数，THP为高压涡轮转矩，TLP为动力涡轮转矩，H为高压涡轮转子的转动惯量，J为动力涡轮转子的转动惯量，KP_Ng和KI_Ng为高压涡轮转速PI控制器的比例积分值，Ng_ref为高压涡轮转速指令、NP_ref为动力涡轮转速指令、KP_Np和KI_Np为动力涡轮转速PI控制器的比例积分值。为了简化分析，速度均由角速度表示。高压涡轮转速控制器按照Ⅰ型系统进行校正，校正后的高压涡轮转速可等效为一阶延时环节，如式(2)所示。燃气轮机双闭环控制回路可简化为单闭环控制，如图8所示。

(2)

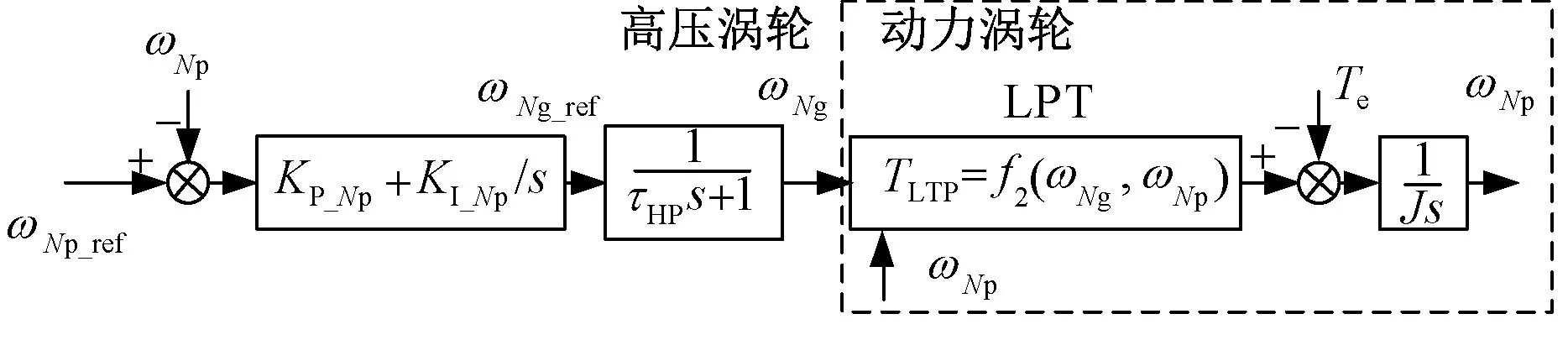
图8 简化后系统框图

对燃气轮机模型在稳态工作点做小信号处理可得到小信号模型, 小信号变量用字母上加“^”表示。

(3)

(4)

(5)

式中，ωNg和ωNg_ref分别为高压涡轮角速度和角速度参考；ωNp为动力涡轮角速度。

由此可得到燃气轮机动力涡轮的开环传递矩阵：

(6)

式中，输出阻抗ZT=1/(sJ-a4)；控制输出传递函数Gco=(a2+2a3ωNg0)/(τHP+1)(sJ-a4)。

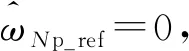
Zo-c=ZT/(1+Li)

(7)

式中，Li=(KP_Np+KI_Np/s)Gco。

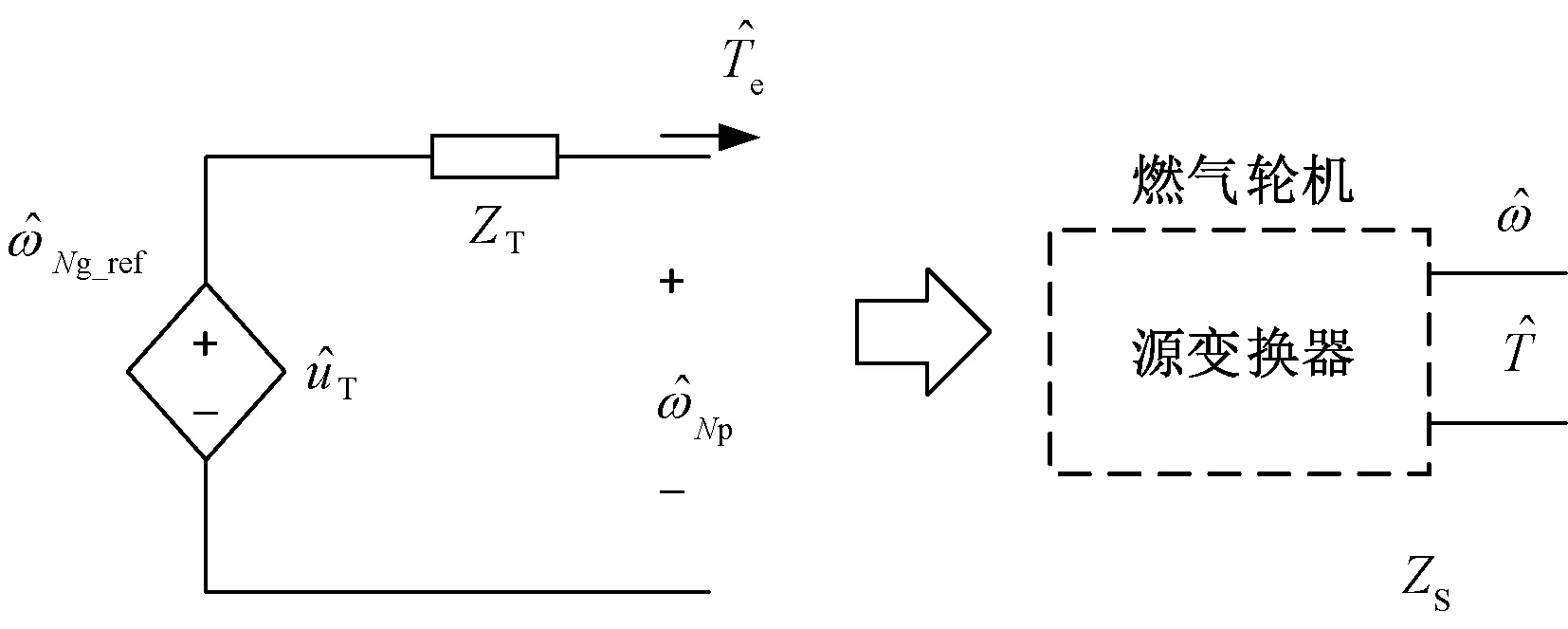
图9 燃气轮机小信号阻抗模型

3.2 电机及变换器小信号阻抗模型

将发电机整流器整体进行分析，其输入为(Te,ωe)，输出为(vdc,iL)，得到发电机及整流器阻抗模型，如图10所示。

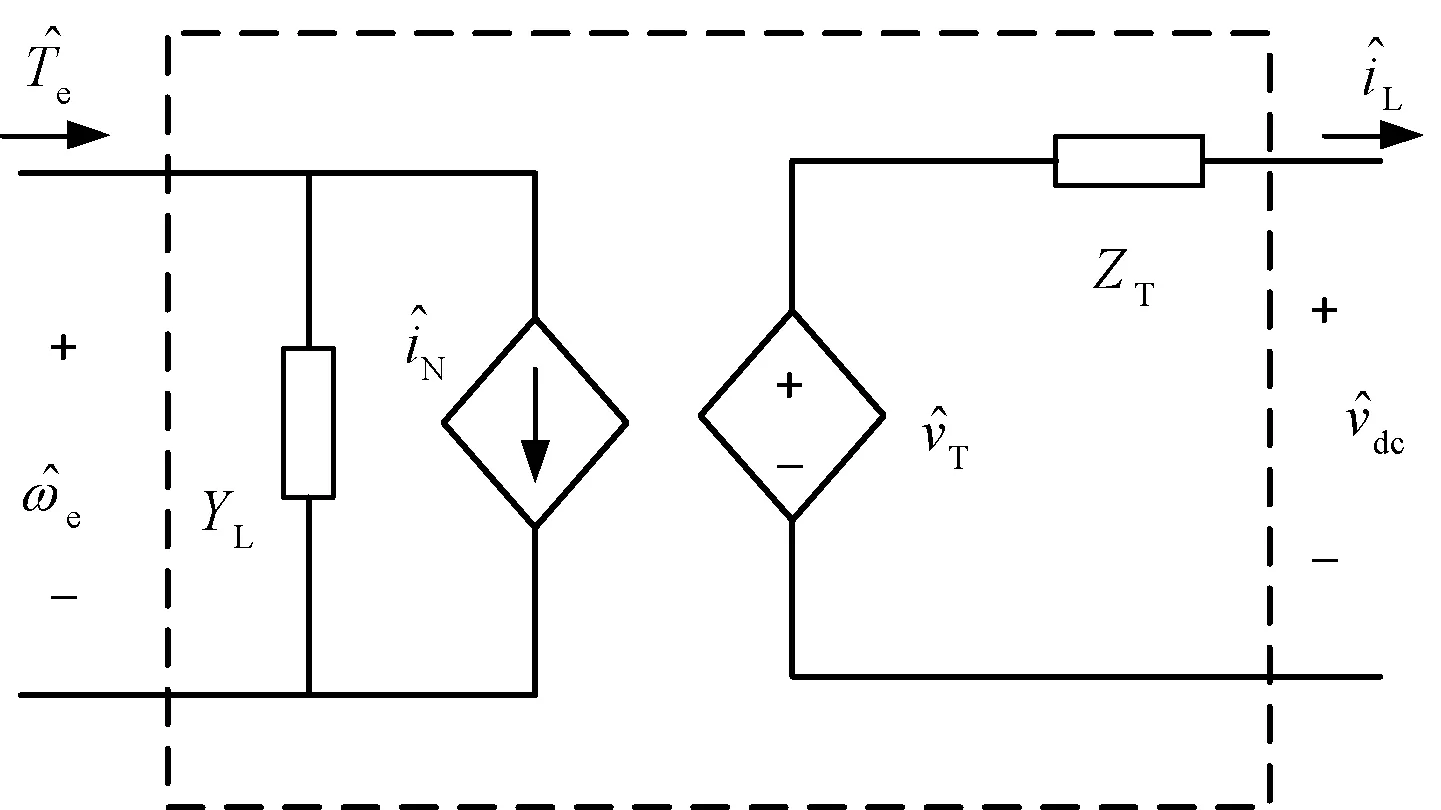
图10 发电机及整流器阻抗模型

发电机及整流器的dq轴模型为[21]：

(8)

(9)

(10)

(11)

式中，R为定子绕组电阻；Ld、Lq分别为dq轴电感；id、iq分别为dq轴电流；vd、vq分别为dq轴电压；ωe为电磁角速度；φf为永磁磁链；np为极对数；Te、TL分别为电磁转矩及负载转矩；C为直流侧电容；iL为直流侧负载电流；Dd和Dq分别为开关函数的dq轴分量。

对式(8)～式(11)在平衡点，Dq0=ωeφf/Vdc0，Iq0，Vdc0附近做小信号处理，稳态值用字母加“0”下标表示，小信号变量用字母上加“^”表示。

(12)

化简式(12)可得发电机整流器开环传递函数矩阵：

(13)

加入电压电流双闭环控制，得到发电机及整流器的小信号双闭环控制框图，如图11所示。其中，

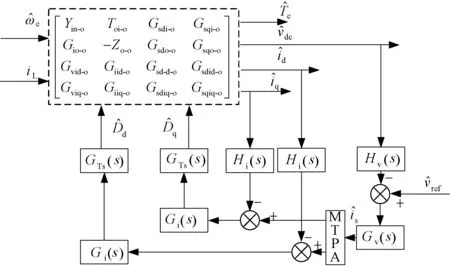
图11 发电机及整流器电压电流双闭环控制

电压、电流采样过程传递函数分别为：Hv(s)=1/(Ts+1)、Hi(s)=1/(Ts+1)，其中Ts为采样周期。

由此可得到以发电机及恒压控制PWM整流器整体的小信号阻抗模型，如式(14)所示，可等效成二端口网络，如图12所示。其中H11，H12，H21，H22见附录。

(14)

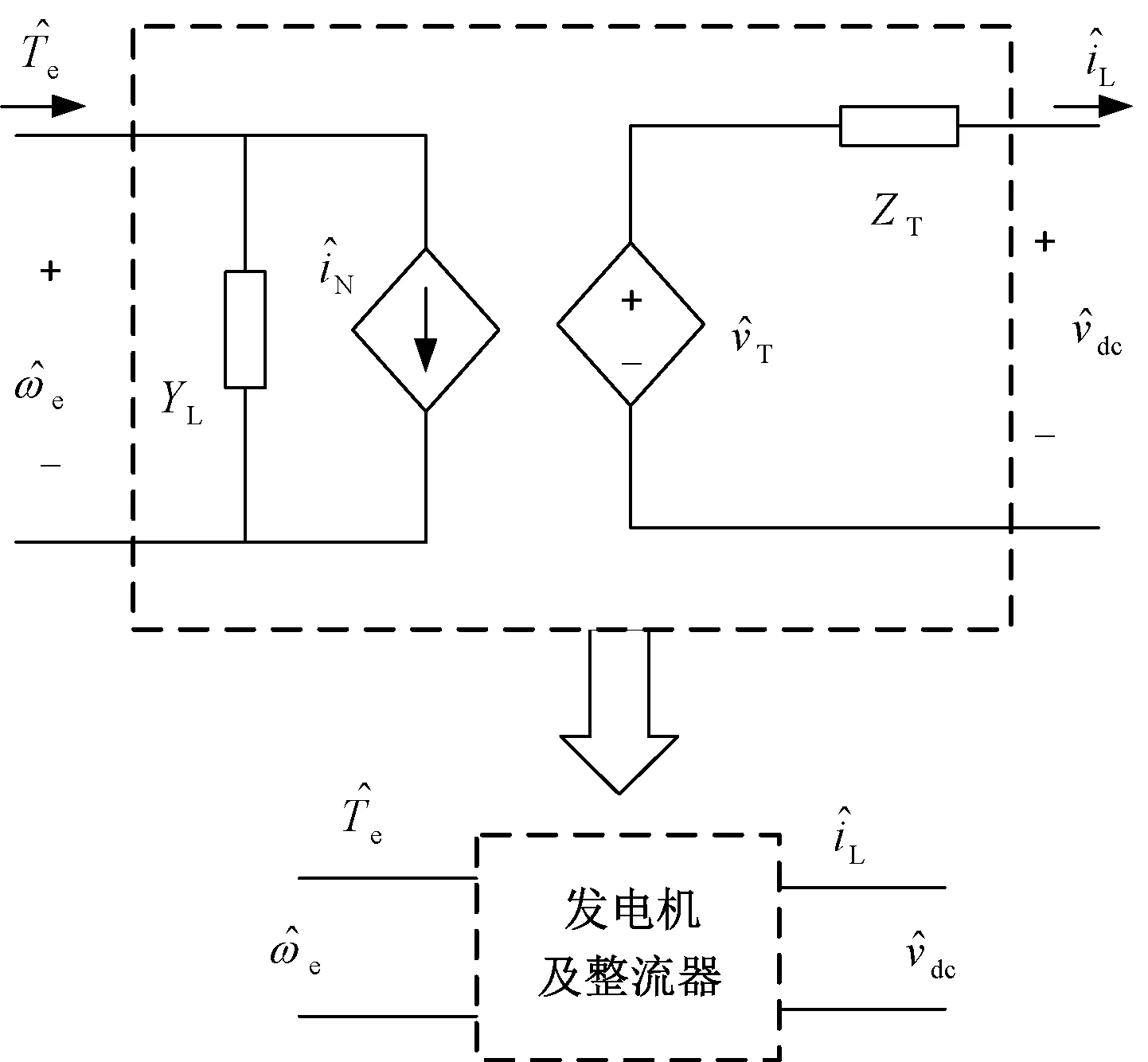
图12 发电机及整流器的小信号阻抗模型

类似的，对电动机及逆变器负载，规定其三相电流及逆变器变流与发电机及整流器相反。可等效成二端口网络，如图13所示。

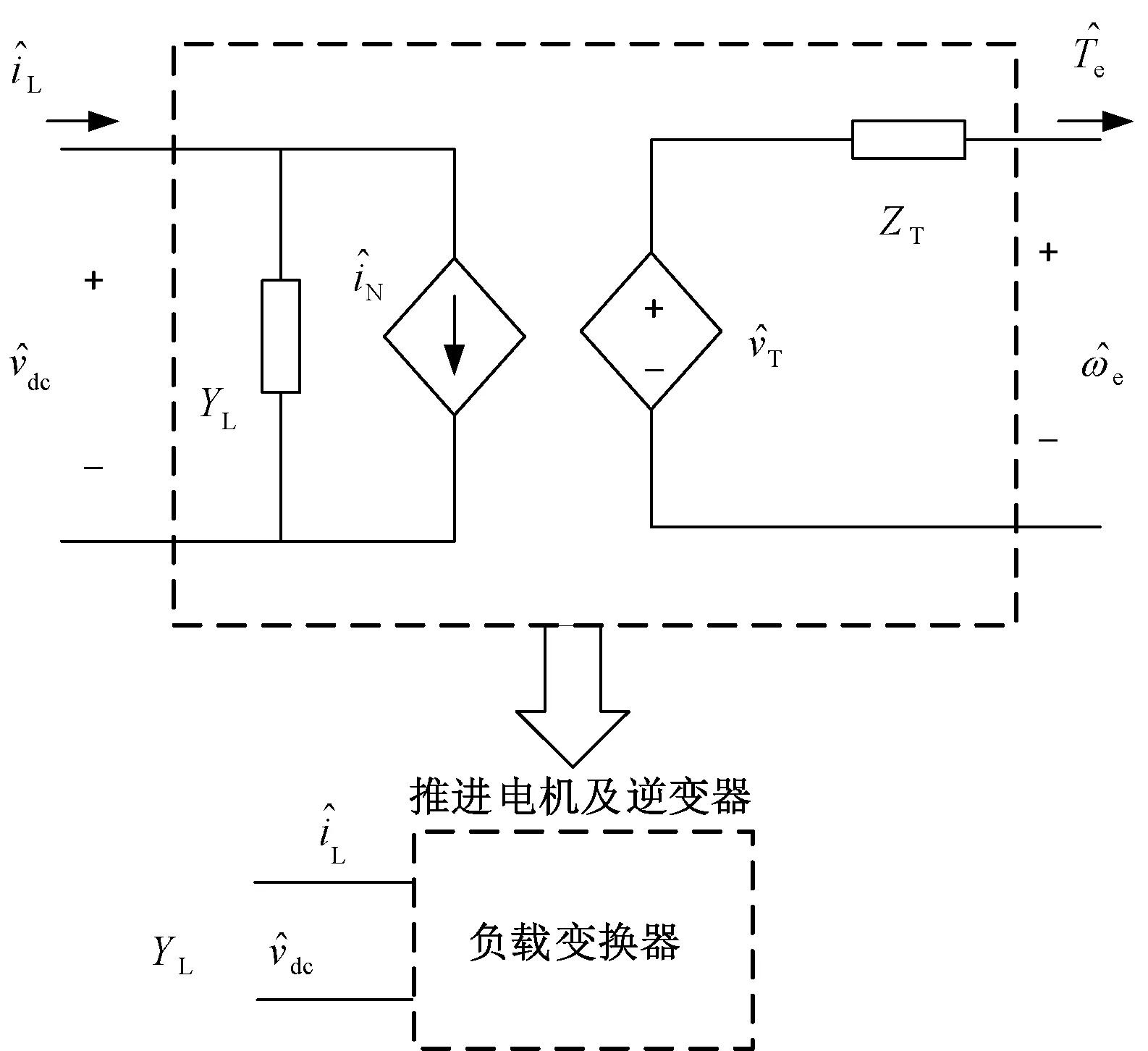
图13 电动机及逆变器的小信号阻抗模型

系统输入导纳为：

(15)

式中，Zc=sC；Zq=sLq+R；Zj=sJ。

4 系统小信号阻抗分析及仿真验证

4.1 混合动力系统小信号阻抗模型

为了分析混合动力系统的小信号稳定性，首先需要建立系统小信号阻抗模型，由于系统通常由多级变换器串并联组成，其源、负载变换器及中间变换器的相互作用，使得系统的稳定性问题变得过于复杂。若进行系统小信号分析，需要将系统简化成二级源负载系统进行阻抗分析，如图14所示。

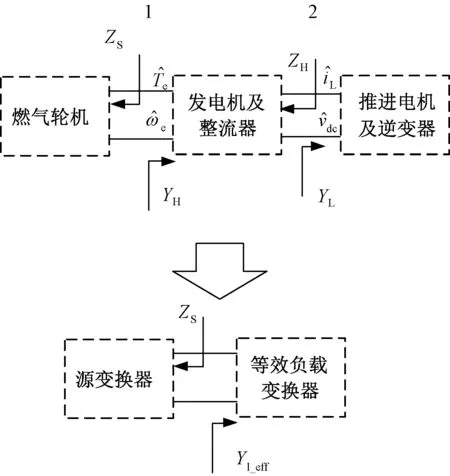
图14 系统源变换器及等效负载变换器

图14中，YH和YL分别为发电机整流器和逆变器的输入导纳。其中，发电机及恒压控制PWM整流器整体既是燃气轮机的负载变换装置，同时也是逆变器负载的源变换装置。

首先针对1处的小信号稳定性进行分析，将发电机整流器作为负载考虑。

1端口后端变换器为发电机及整流器、逆变器及电动机负载，为了对系统1端口进行小信号分析。首先要判断PWM整流器与推进电机逆变器之间端口(端口2)是否满足MPC稳定性要求，若满足则可以按等效简化规则将其等效为一个新的电力变换装置，新的负载输入导纳为：

(16)

对于表1所示的系统参数，在0～300 kW负载、90%～110%燃气轮机转速等工况计算整流器输出阻抗及禁止域，逆变器的输入导纳并没有进入由整流器输出阻抗为基础的禁止区域之中，如图15所示。因此2端口满足稳定性要求，可以将发电机整流器及逆变器负载等效为一个新的电力变换装置即等效负载变换器Leff。此时仅需要分析燃气轮机与Leff的稳定性，就可判断系统在1端口处的小信号稳定性。

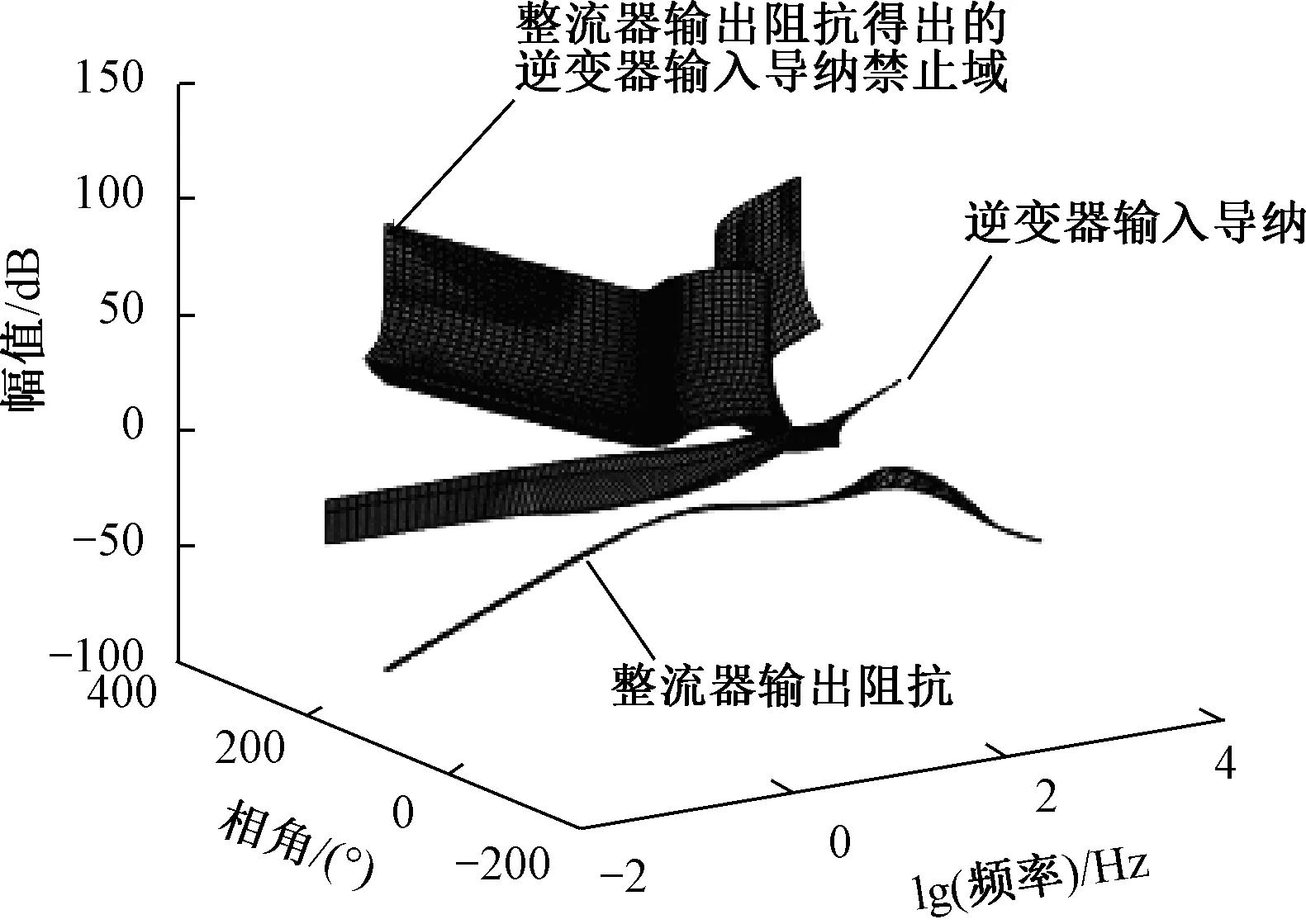
图15 逆变器输入导纳及其禁止区域

燃气轮机输出阻抗禁止域与燃气轮机等效负载Leff输入导纳，如图16所示，可以看出Leff的闭环输入导纳于0.05 Hz进入了禁止区域，系统可能存在小信号不稳定现象。

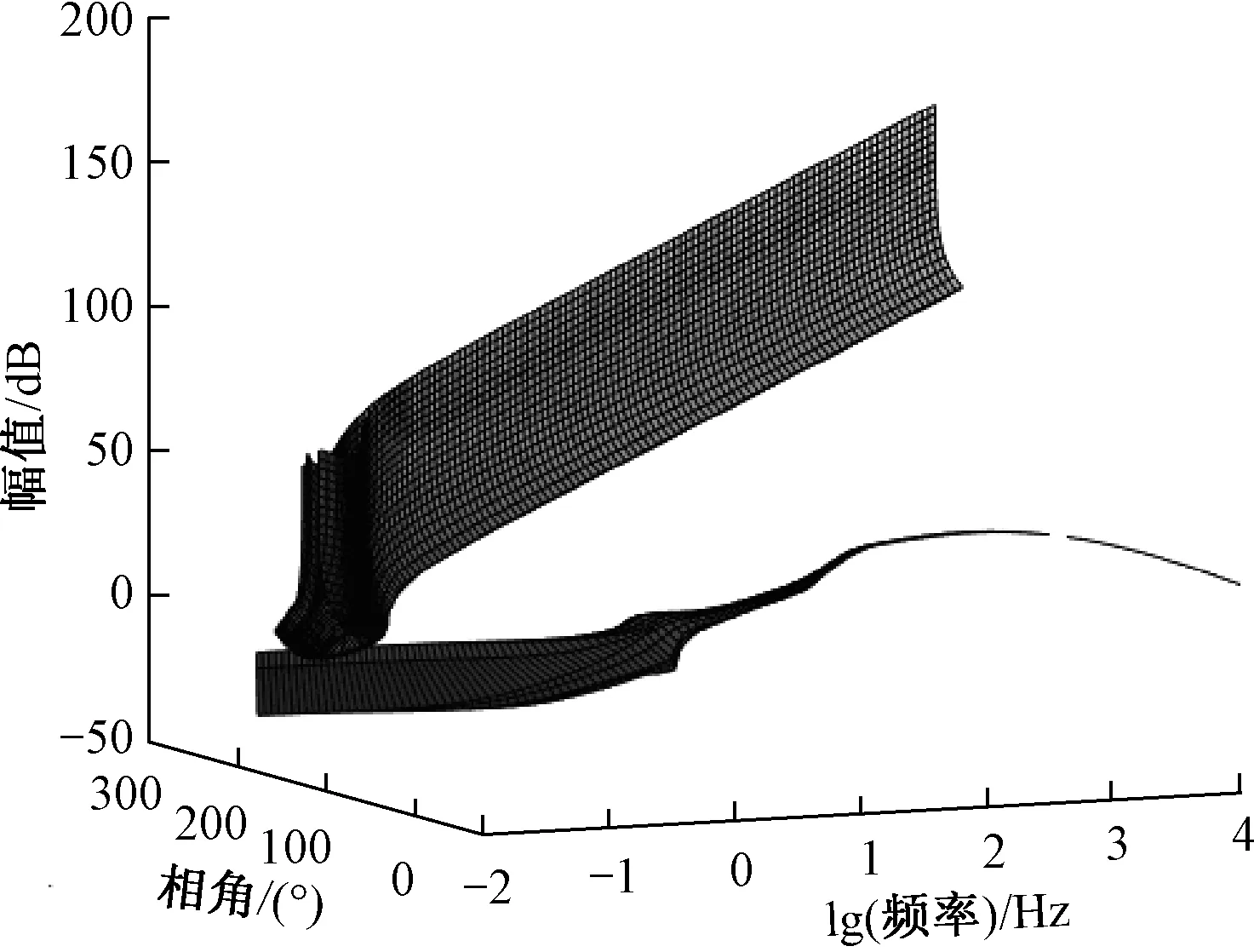
图16 等效源变换器禁止区与等效负载变换器输入导纳

4.2 整流器前馈补偿控制

针对发电机整流器存在的恒功率负阻抗特性，可以从阻抗补偿的角度来改善系统稳定性，满足稳定条件。

为改善系统小信号稳定性，引入了一种转速前馈补偿控制，转速前馈控制小信号框图如图17所示，除了PWM整流器电压电流双闭环控制外，在控制器的电压指令的输入端还引入了转速前馈Gff(s)。

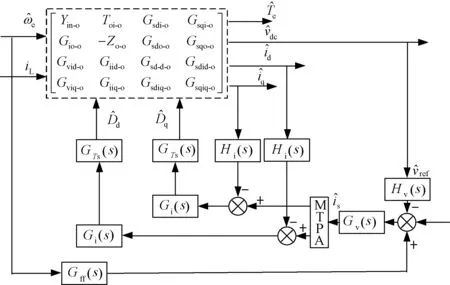
图17 整流器转速前馈控制小信号框图

将Gff(s)设计为带通滤波器，设置ω1，ω2使滤波器的带宽覆盖0.05 Hz区域。

(17)

发电机整流器在控制中引入转速前馈控制相当于在其输入端增加一个等效惯量；发电机及PWM整流器输入端即燃气轮机输出端的等效惯量的增加可以降低输入转速的波动，改善系统的小信号稳定性。

引入转速前馈后，整流器及发电机组成的变换器其输入导纳相角的增加使得系统的相角裕度增加，输入导纳与导纳禁止区无重叠，提高了系统稳定性，如图 18所示。为了验证本文所提出方法的有效性，在Matlab/Simulink按照实际系统拓扑搭建系统模型，并在发电机整流器直流侧施加负载扰动，得到燃气轮机转速响应结果，如所图19所示，由图 19的仿真结果可以看出，加入补偿前，系统于1 800 s时加入负载扰动，动力涡轮转速发散，系统小信号不稳定，加入补偿后，燃气轮机转速稳定性明显提升，证明前馈补偿控制可以改变发电机整流器作为燃气轮机负载时带有的负阻抗特性。

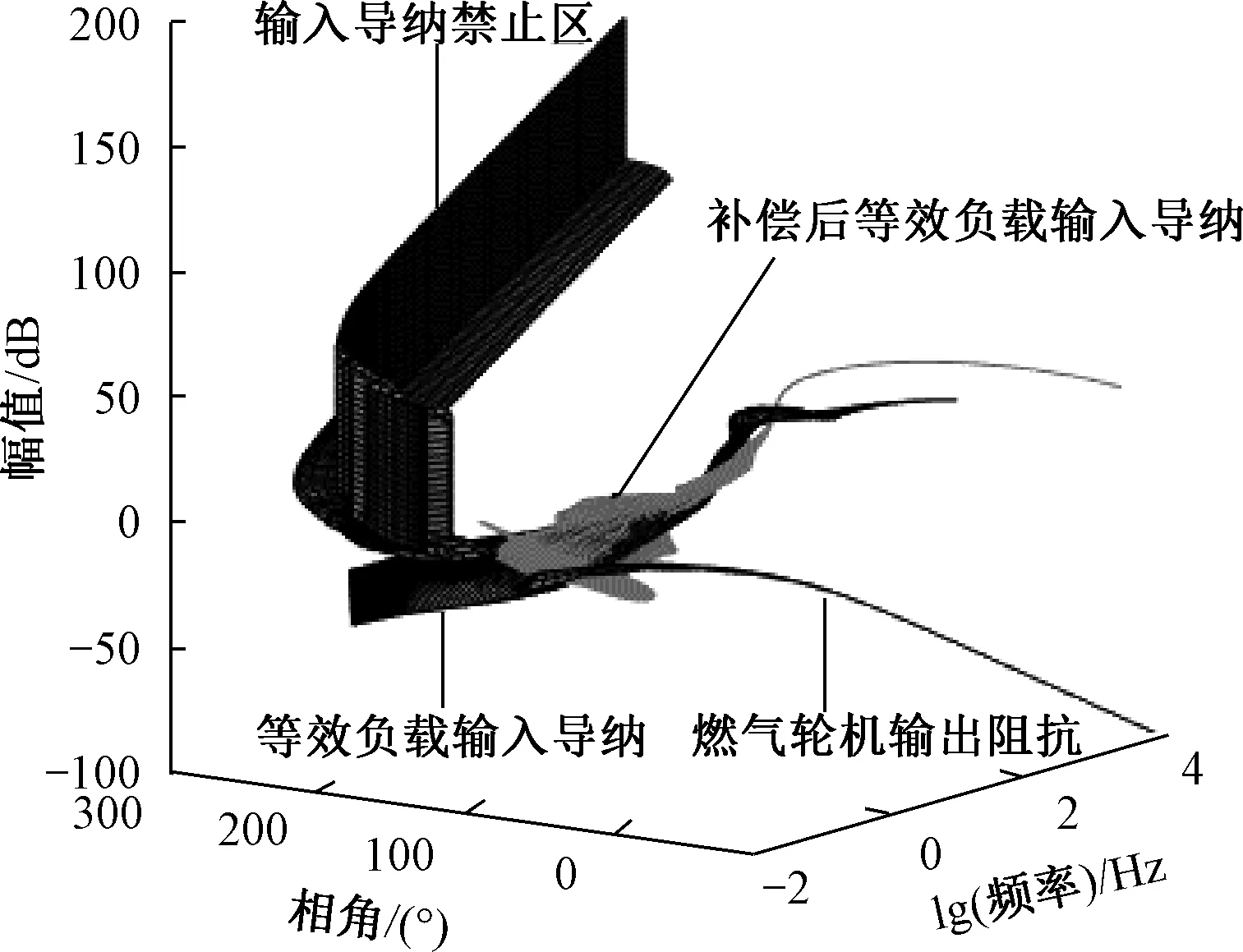
图18 等效源变换器的禁止区与加入前馈补偿的等效负载变换器的输入导纳

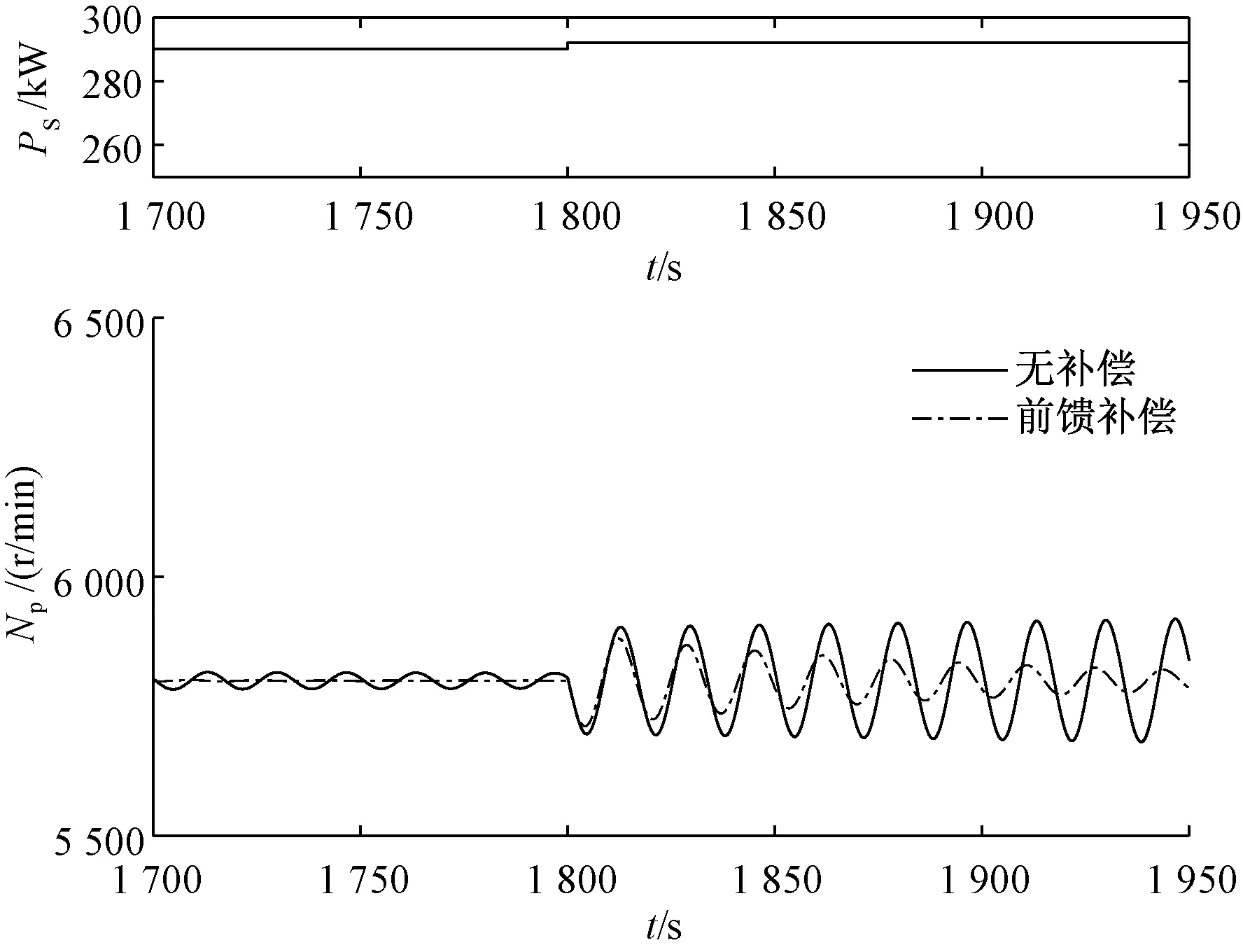
图19 燃气轮机输出转速仿真结果无补偿器和带补偿器

为了验证本文所提出方法的有效性，搭建了混合动力系统试验平台，如图 20所示，在实验台上进行了对比测试，系统参数如表1所示。当燃气轮机发电转速为5 800 r/min，输出功率为200 kW时，加入负载扰动，测量动力涡轮转速响应，实验结果如图21所示。加入补偿前出现了明显的转速振荡，加入所提出的前馈补偿方法后有效抑制了转速波动，使得燃气轮机发电系统可以在此工况下稳定运行。

图20 系统试验台架

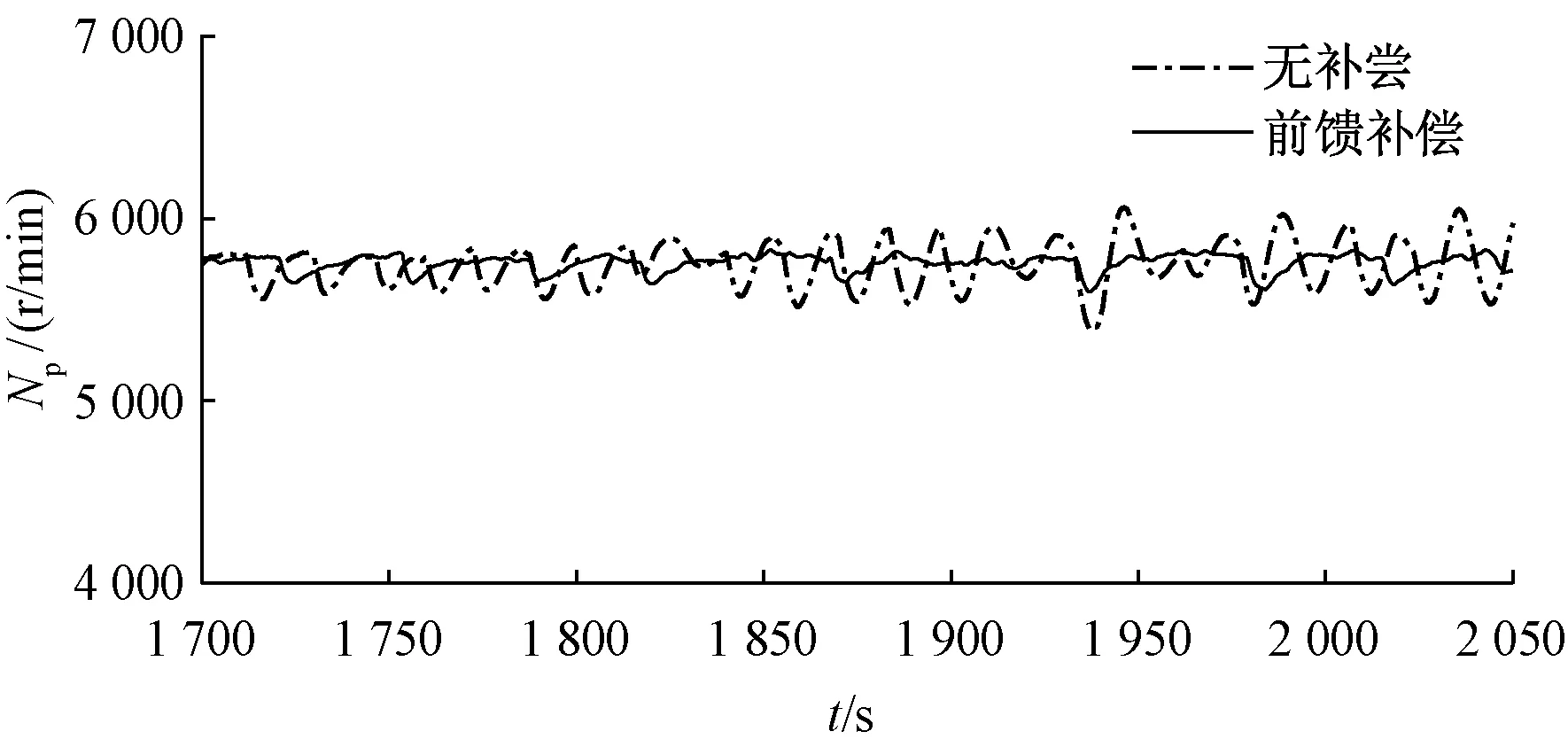
图21 燃气轮机输出转速实验结果

5 结论

本文分析和比较了目前常用的阻抗稳定分析判据，选取保守性较小的MPC标准作为微型燃气轮机发电系统的稳定性判据，并对MPC判据进行了改进，基于MPC标准获得输入/输出阻抗的禁止区域。建立了微型燃气轮机和电力电子变换器的阻抗模型，以混合动力系统整流器为控制对象，从改进控制方法的角度改善其输入导纳，提高了燃气轮机带恒功率负载的小信号稳定性，并得到如下结论：

(1) 由于燃气轮机燃烧过程、高压涡轮及动力涡轮的非线性特性、动态响应慢及动力涡轮输出轴的小惯量特性，其带发电机整流器负载时，会出现小信号不稳定现象，小信号阻抗分析、仿真及实验结果均验证了这一点。

(2) 为了改进发电机和整流器整体的输出导纳，提出了一种转速前馈补偿控制方法，对燃气轮机的转动惯量进行补偿。仿真结果和实验结果证明该补偿控制方法可以使发电机整流器在具有较好的动静态性能的同时，提高燃气轮机系统的稳定性。

附录

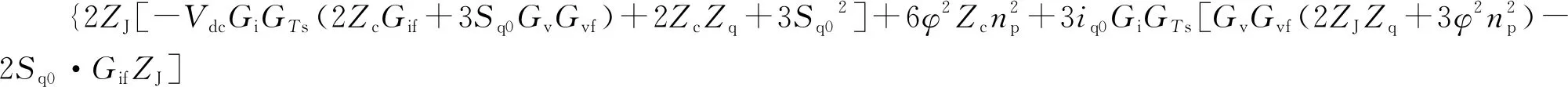
H12=-3φnp(Sq0-VdcGiGTsGvGvf)/[-VdcGiGTs(2ZcGif+3Sq0GvGvf)+2ZcZq+3iq0GiGTs(GvGvfZq-Sq0Gif)+3Sq02]

H21=3φ(Sq0-iq0GiGifGTs)/[-VdcGiGTs(2ZcGif+3Sq0GvGvf)+2ZcZq+3iq0GiGTs(GvGvfZq-Sq0Gif)+3Sq02]

H22=(-2VdcGiGifGTs+2Zq)/[3Sq02-VdcGiGTs(3Sq0GvGvf+2GifZc)+2ZcZq+3iq0GiGTs(-Sq0Gif+GvGvfZq)]