新型配电网同步相量装置测试与实际电网应用

朱 征， 李依泽， 顾黎强， 陆 超， 刘 舒， 王印峰

(1. 国网上海市电力公司电力科学研究院， 上海 200437；2. 电力系统及发电设备控制和仿真国家重点实验室， 清华大学电机系， 北京 100084； 3. 国网上海市电力公司浦东供电公司， 上海 200122)

1 引言

近年来，随着计算机技术、通信技术、电子技术和网络技术的快速发展，我国配电网自动化水平也有了很大程度的提高[1，2]。面向未来新能源高比例渗透，源荷互动频繁的智能配电网，构建实时动态监测与控制网络成为目前配电网建设和研究的重点工作之一，并已得到国家的大力支持——目前有数个国家级重点项目支撑[3，4]。

现有输电网的同步相量测量装置(Phasor Measurement Unit，PMU)能够提供相角测量和系统全局动态状态信息，已经在输电网动态监测和稳定控制领域得到了广泛应用[5,6]。然而由于配电网节点包括居民负荷、大型工业负荷以及分布式新能源接入点等，配电网谐波及间谐波等干扰复杂且严重，信号动态特性丰富，配电网测量环境恶劣，同时由于配电网线路通常很短，线路两端母线电压的相角差较小，对配电网PMU装置精度提出了更高的要求。现有关于配电网电能质量[7-9]和相量测量[10,11]等方面研究成果也从不同方面说明了配电网的这一特点。

近几年，配电网同步测量技术与配电网PMU装置得到了快速发展。美国PSL公司研制的μPMU装置[12]在结构和功能上比较贴近配电网实际需求。该装置相角测量误差标称不高于0.01°，但仍存在装置成本高、防护等级不够，动态响应性能欠佳等问题。美国Yilu Liu团队研制的频率扰动记录仪装置[13]，测频精度可以达到0.000 5 Hz，但对实际配电网中间谐波干扰抑制能力不足。上述PMU装置与算法虽考虑到了配电网的高精度测量需求，但无法同时兼顾测量精度和动态响应性能。同时未对实际配电网系统的信号进行分析，难以应对实际配电网复杂多变的场景，缺乏依靠实际装置对算法进行验证分析。

本文提出一种基于频率分析和自适应滤波器的新型配电网同步相量算法，并在基于片上系统的微型多功能同步相量测量单元(Multifunctional Micro Phasor Measurement Unit，μM-PMU)中实现了该算法。搭建了高精度同步相量测试平台，并利用此平台对测量装置进行符合配电网环境特征的多场景测试验证。上述μM-PMU装置已在上海临港地区进行示范应用，并进一步建立了配电网同步测量系统。利用该实际系统的信号数据对配电网信号特征进行分析，并对本文所提的相量算法的有效性与准确性进行验证。

2 高精度新型配电网同步相量算法

2.1 频率成分在线分析与自适应FIR滤波器设计

基于窗函数设计FIR滤波器在相量算法应用普遍。然而配电网中具有较多难以滤除的频率成分，这些频率成分处于滤波器的过渡带，使得现有相量算法难以应用于配电网环境中。本文应用一种基于频率成分在线分析的带陷波齿的FIR滤波器，根据配电网频率成分的在线分析结果，实现滤波器中心频率和陷波齿位置的自适应调整，有效提高配电网多干扰场景下的相量计算精度。

在频率成分在线分析方面由于现代谱估计技术的旋转时不变技术(Estimating Signal Parameters via Rotational Invariance Technique， ESPRIT)[14,15]，具有频率分辨率高，抗噪性好的特点。因此本文采用ESPRIT方法对信号的频率成分进行在线分析。

由于Cosh窗函数[16]过渡带相对较窄，旁瓣衰减幅度较大，综合性能优异，本文滤波器设计采用该Cosh窗。其次，由于窗函数阶数越高，其主瓣宽度和旁瓣衰减特性均可以改善，但会导致动态过渡过程变长。因此，在稳态情况下，选择4周波的Cosh窗，动态情况下选择2周波的Cosh窗来设计滤波器。4周波FIR滤波器的频域衰减特性如图1所示。

图1 带陷波齿FIR滤波器的频域特性

2.2 动/稳态切换相量算法框架

因此，本文将FIR滤波器、频率分析和状态识别等融为一体，设计了可在线自适应调整的相量算法框架，如图2所示。

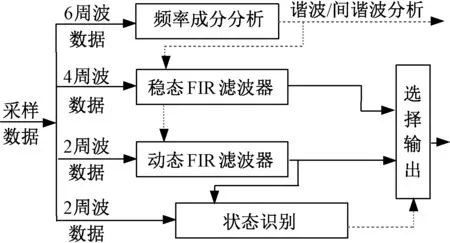
图2 动态切换相量算法的整体框架

算法主要包括四个通道：稳态相量计算，动态相量计算，频率分析和状态识别，各通道功能及其之间的关系介绍如下：

稳态相量算法通道：基于考虑带外干扰影响的稳态FIR滤波器，实现稳态场景下基波相量的高精度计算。进而，利用相位差计算频率和频率变化率，并对频率和频率变化率进行滤波。

动态相量算法通道：基于动态FIR滤波器，估计动态信号场景下的基波相量及其导数，并计算出基波幅值/相位的一阶和二阶导数，进一步得到频率和频率变化率。

信号频率分析通道：进行信号频率成分的在线分析，本文利用六周波数据。使用ESPRIT方法，对信号频率成分进行分析。

状态识别通道：利用动态相量导数的估计值，通过对幅值和相位导数在一段时间内积分，若积分F大于一定阈值，则可以判断信号幅值和相位是否发生了突变。

(1)

式中，A(t)′为基于动态FIR滤波器计算得到的相量幅值一阶导数；φ(t)′为相量相位一阶导数；积分时间间隔t0～t一般设置为200 ms。

3 高精度同步相量测试平台

3.1 高精度测试平台介绍

因现有PMU测试仪、继保测试仪等装置相角精度不高，不适用于配电网同步相量算法与配电网PMU装置的测试和研发需要。为此，搭建了具备高精度相量测试能力的物理试验平台。该平台的设计原理图如图3所示，主要由高精度同步波形发生器、模拟主站系统、高精度时钟、卫星天线、待测PMU和待测同步时钟等装置等组成。

图3 配电网高精度同步相量测量装置综合测试平台

(1)高精度同步波形发生器。采用OMICRON(CMC 256 plus)6相电流+4相电压测试装置与通用校准仪器，该仪器支持含多谐波、间谐波信号及幅值/相位阶跃等动态信号的发生，可为PMU测试提供带时标的多种测试信号。频率误差不高于0.000 5 Hz，幅值误差不高于0.02%，相位误差不高于0.005°。

(2)高精度同步时钟装置。PMU测试平台高精度时钟信号源，外接北斗/GPS天线，内部采用铷原子钟，具有远高于普通恒温晶振的频率稳定度、温漂和老化率。授时精度不低于10 ns，为PMU装置内置时钟模块与高精度同步波形发生器提供精准时钟信号。

(3)模拟主站系统。是测试平台的控制和分析中心。主站以实际电网的WAMS主站为基础开发实现，具有前置通信和各类数据分析服务功能。其中，可以对实时测量数据进行观察和分析。服务数据库包括实时库和时序库模块等。实时库初始化从商用库中加载配置信息，保存有前置通信系统所需的配置信息。时序库主要存储PMU实时和历史数据，并通过时间选取历史存储数据，可实现曲线查询或转换为CSV文件保存，便于离线分析。

实验室高精同步相量测试平台的测试原理为在基于北斗/GPS的高精度同步时钟授时的情况下，高精度同步波形发生器根据主站系统设定的波形曲线发出带时标的模拟信号，由经由待测PMU测量并将测量值送回模拟主站系统进行误差分析。

3.2 符合配电网环境特征测试与验证

配电网和输电网测量信号的区别就是前者含有更加丰富的谐波和间谐波干扰成分，且这些成分可能会同时存在。因此，本文相量算法的设计的目标就是能够满足含多谐波/间谐波干扰场景下的高精度测量需求。

这里根据实际某电动车快充站接入点处电流信号的干扰特征，模拟构建一个含有多个谐波、间谐波干扰的测试信号：其中测量信号的基波频率设为49.98 Hz，含有8.96% 的5次谐波、4.40%的7次谐波、2.32% 的11次谐波、0.96% 的13次谐波和1.36% 的17次谐波。此外，在信号中增加两种间谐波干扰成分，分别是：1%的0.5次间谐波和1%的1.5次间谐波。计算得到模拟信号的谐波/间谐波总畸变率THD为10.48%。在此基础上，考虑实际信号中可能还含有50 dB噪声。

此外，为了更加直观地反映本文所提出的带陷波齿自适应FIR相量算法(Notch-Tooth attached FIR，NT-FIR)在各种场景下性能水平，这里分别选择IEEE标准[17]中推荐的M级滤波算法(M-FIR)[18，19]以及目前相关研究中具有代表性的两种方法——扩展卡尔曼滤波方法(EKF)[20]和递归小波变换方法(RWT)[21]作为对比。各方法性能对比结果见表1。

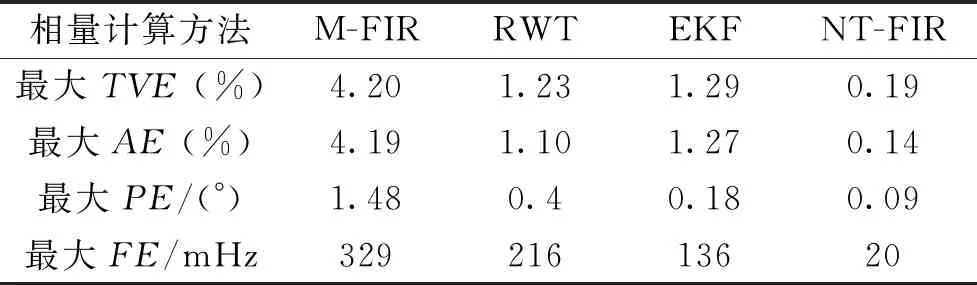
表1 多谐波、间谐波场景下各相量算法性能对比

可以明显看出，含有多种干扰成分的信号对现有的同步相量算法提出了严峻的挑战，M-FIR、RWT和EKF相量算法的TVE指标均超过1%。因为，这些算法常常只考虑一种间谐波干扰成分，且该干扰成分的频率通常是假设已知的，这显然与实际情况不符。相比之下，本文所提出的NT-FIR算法，TVE指标仅为0.19%，幅值误差为0.14%，相位误差也在0.09°左右，充分显示了该算法的高精度计算性能。

此外，基于测试平台所具备的故障场景模拟功能，模拟了配电网多种故障场景，对所研制的PMU原理样机进行测试。值得注意的是应该认识到，配电网短路故障应该是在多干扰场景下的动态过程，这里设置一个典型的三相短路故障场景对算法的整体性能进行评估：信号频率50.5 Hz，其中含有3、5、7次谐波以及135 Hz间谐波，谐波/间谐波总畸变率为11.2%。系统电压在0.4 s时发生三相短路故障，电压跌落到0.3 pu，0.8 s保护动作清除故障，电压恢复到0.9 pu，由于系统阻尼不足，电压信号伴有调制频率5.0 Hz，初始为0.1 pu，时间常数为0.50的指数衰减振荡过程。下面给出电压A相的幅值测试结果，如图4所示。

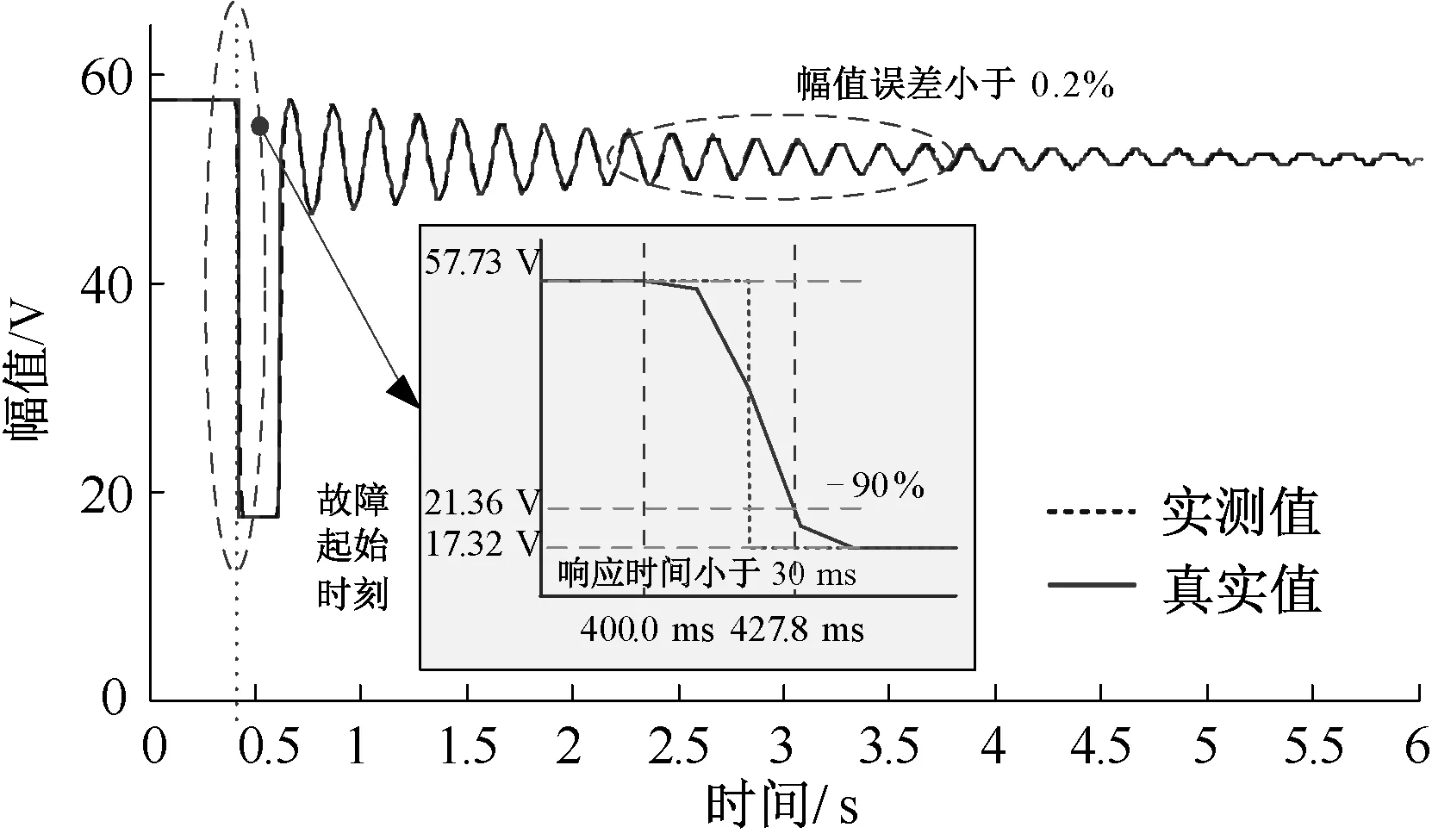
图4 单相短路故障场景下的测试结果

可以看出，PMU原理样机在电压跌落和恢复过程中具有较快的响应速度，其中故障跌落过程响应时间仅为27.8 ms，在恢复后的衰减振荡过程中，其TVE误差也不大于0.2%。在上述动态场景下，为进一步验证所提算法的有效性，分别与EEE标准中推荐的P级滤波算法(P-FIR)，RW和EKF方法的仿真结果进行对比，结果见表2。

表2 动态场景下各相量算法性能对比

由上述结果可知，所提算法的结果具有更快的阶跃响应速度与动态调制过程中的精度。该结果有效验证了该装置具备快速、准确响应测量信号动态变化的能力。

4 配电网同步测量系统

受国家重点研发计划项目《基于微型同步相测量的智能配电网运行关键技术》支持，在上海市临港地区建立了以配电网PMU装置为基础的配电网同步测量系统。临港地区区内阳光充足，近远海风电资源丰富，电力大用户数量在500余户，电动汽车接入发展迅速。该系统覆盖220 kV～400 V全部配电网电压等级，电动汽车快充电站接入点、分布式光伏/风电并网点共计20余个。预期将会共部署近百台配电网PMU装置，测点数量百余个。

同时为满足系统对于配电网运行状态的感知和控制需求，建立了基于同步相量信息的智能配电网运行分析与协调控制系统主站。除接受配电网PMU发送的同步相量外，该系统还集成了EMS系统数据、DMS系统数据、用采系统数据和PMS系统数据，满足智能配电网运行与控制需求。其主站系统硬件架构如图5所示。

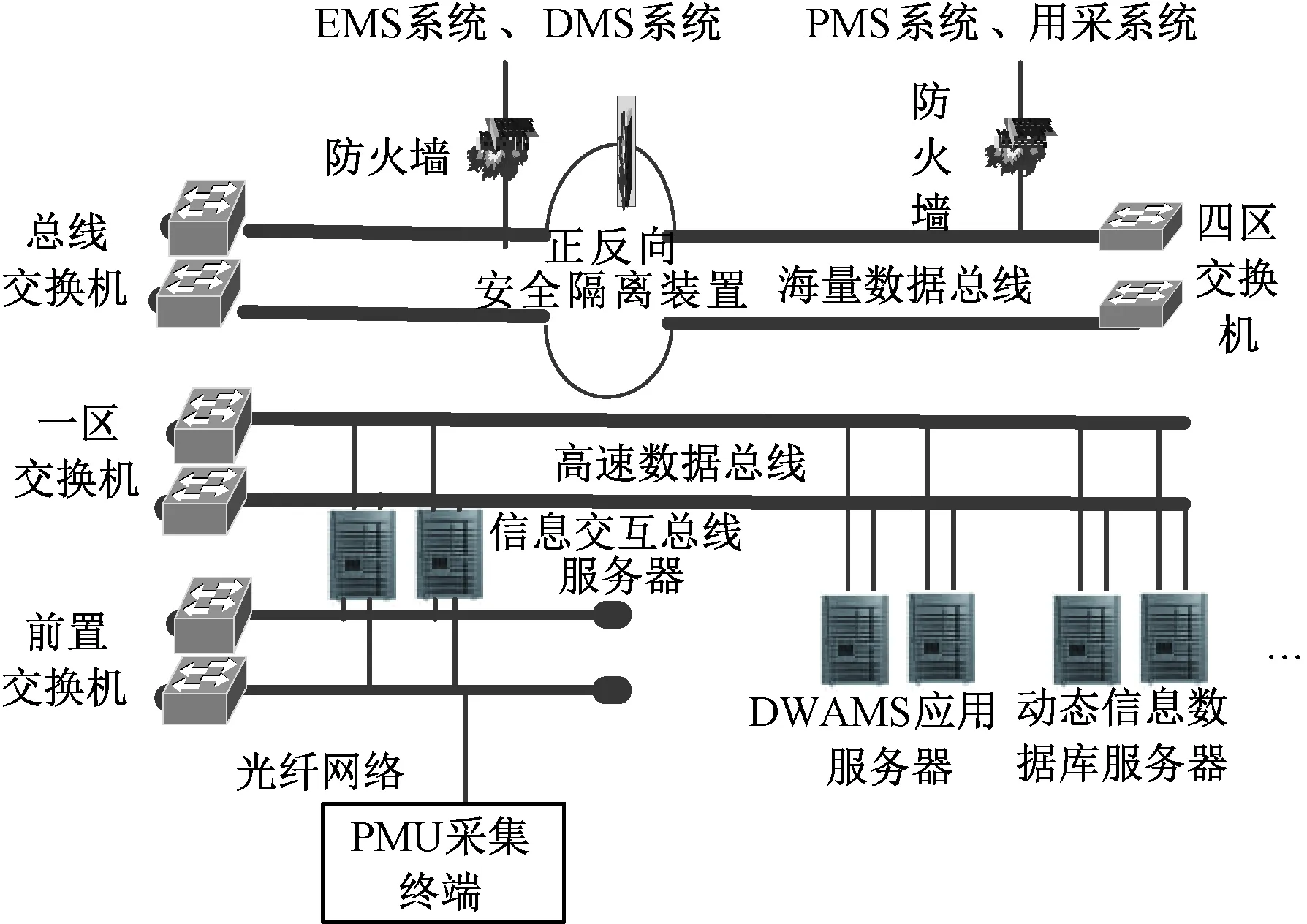
图5 智能配电网运行分析与控制系统主站架构图

5 配电网实测同步相量数据分析

5.1 不同场景信号特征分析

配电网PMU的安装位置可能是居民负荷、大型工业负荷以及分布式新能源接入点等，相对输电网更加复杂多样。不同测量点的谐波、间谐波等干扰成分以及信号的动态变化特征各不相同，这些进一步增加了配电网同步相量高精度测量实现的难度。

基于从上述配电同步测量系统收集到的配电网实测数据，对配电网具有代表性场景下的测量信号特征进行全面地分析。包括新能源发电接入点、电动车充电站接入点、工业负荷接入点。

5.1.1 新能源发电接入点

新能源发电大多通过换流器等电力电子装置接入电网，由于交直流转换间的非线性相互作用，给系统注入了大量谐波和间谐波等干扰成分。对第4节所述系统10 kV电压等级下的新能源接入点测量信号干扰情况分析，利用配电网PMU装置对接入点的电压、电流模拟采集量进行连续录波。

信号频率成分分析结果显示，观测时间段内，以某接入点A相电压和电流为例，干扰成分数目及含量情况如图6所示。由于观测时间正处于中午光伏出力较大的时刻，电流信号中谐波数量及其含量均远高于电压信号，其中5次、7次、11次和17次谐波含量较高。电压、电流信号中5次谐波的含量最高，电流5次谐波含量超过了5.2 %。3次谐波含量也在2.5 %以上。

图6 该光伏接入点的电压和电流的谐波/间谐波分析结果

5.1.2 电动汽车快充站接入点

对某630 kW电动公交快充站点的10 kV母线电压和出线电流实测数据进行分析，其谐波和噪声含量如表3所示。

表3 电动车充电站点谐波畸变率和噪声水平

可以看出，该测点电流无论是谐波畸变率还是噪声水平均高于电压，电流的SNR为52 dB左右，低于电压SNR 67 dB的噪声水平。对比电压和电流B相和其余两相的干扰水平可以看出，B相的谐波含量和噪声干扰水平均低于A、C两相，说明同一测点，由于三相负载不对称，可能会导致不同相的干扰水平存在差异。

对A相电流的谐波和间谐波干扰成分进行分析，其种类和含量如图7所示。

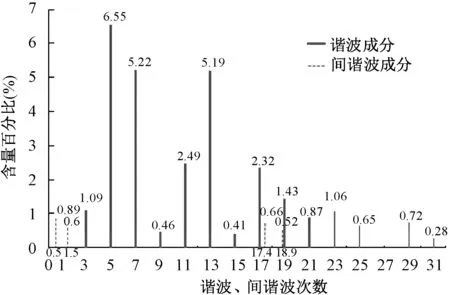
图7 电动车充电站接入点电流信号干扰成分

可见，电流信号中不仅含有大量谐波干扰，还含有0.89%的25 Hz、0.6%的75 Hz、0.66%的870 Hz和0.52%的945 Hz间谐波干扰。这些种类丰富、含量较高的干扰成分，尤其是间谐波成分，对电流基频相量的计算提出了严峻地挑战。

5.1.3 工业负荷接入点

以某35 kV变电站接入某化工负荷的10 kV出线为例，分析由于工业负荷投切导致的配电网电压波动情况。其电压波动情况如图8所示。

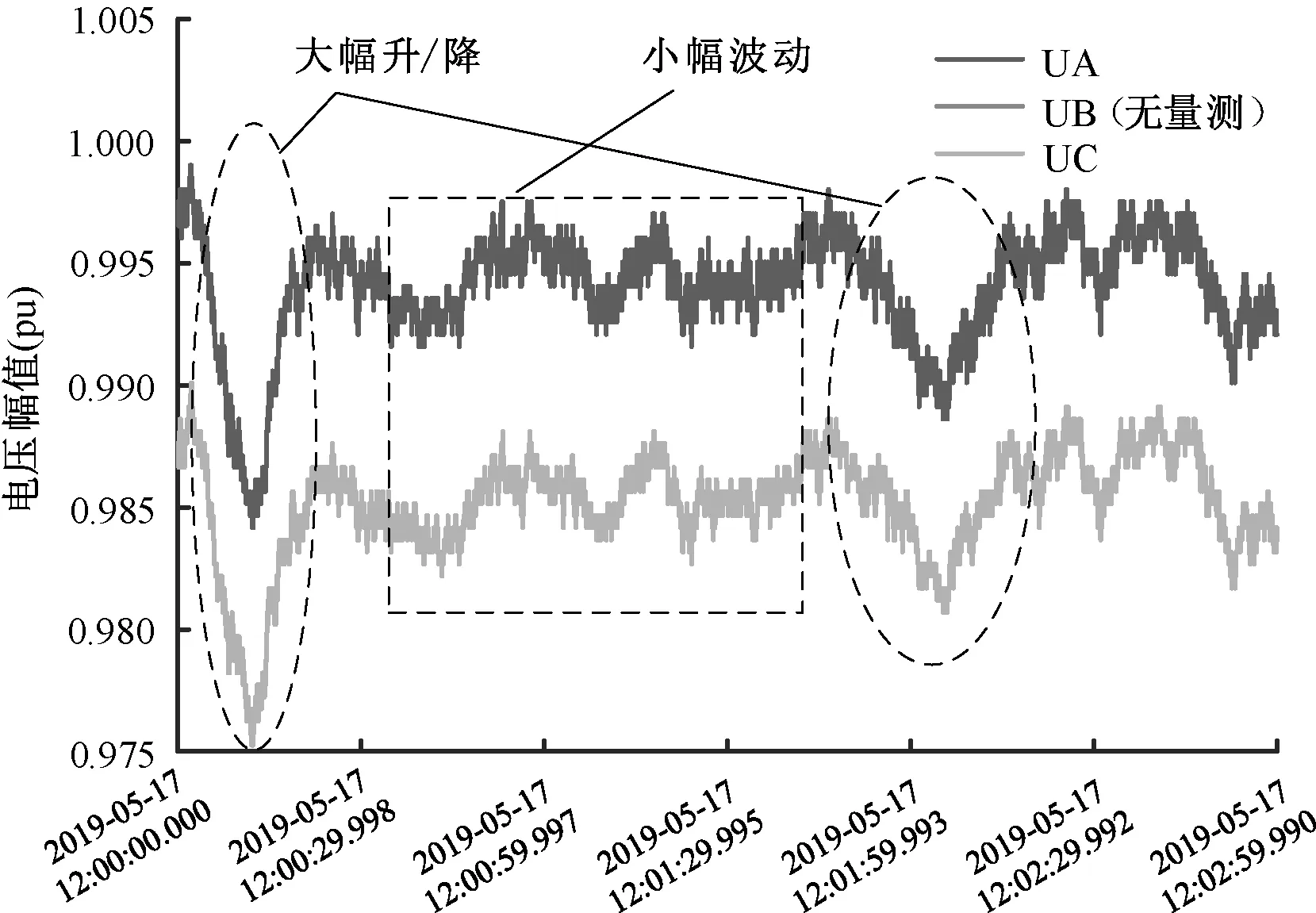
图8 某化工负荷接入点电压幅值波动曲线

可以看出，该化工负荷具有冲击负荷类似的特性，由于功率短时间内增加导致电压出现跌落，跌落幅度最大达到1.5%。值得注意的是，即使在电压没有出现跌落的时刻，除去系统测量噪声(图8中密集的波动变化)，电压幅值也存在小幅波动趋势，说明实际信号常伴随小幅波动。

5.2 算法运行性能评估

下面结合实际系统安装配电网PMU装置运行数据，算法与装置的现场运行的性能进行分析评估。首先，选取配电网多条线路，对线路两端PMU数据进行连续1h动态录波(216万点数据)，分析各线路的两端电压相位曲线，发现装置运行具有很好的测量稳定性，以某两条10 kV线路两端三相电压相位差连续录波数据为例，如图9所示。

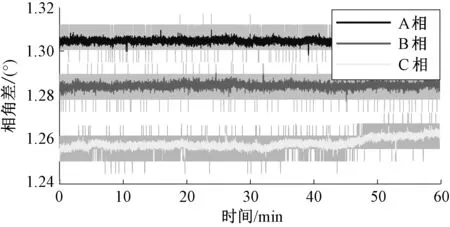
图9 配电网某条10 kV线路端电压相位差曲线

可以看出两条线路各相电压相位差均运行平稳，经过统计，99%以上的相位差位于其趋势线(经过滤波得到，反映了变化趋势)±0.01°范围内，没有出现偏差较大的坏数据，说明了现场安装PMU具有较高测量稳定性和可靠性。

其次，某条10 kV线路PMU布点较密集，其布点间隔均在100～200 m之间，随机选择三个时间断面，对沿出线方向部署的四台PMU装置电压相位测量关系进行分析，显示了相对于线路起始点的A相电压相位关系。结果如图10所示。可以看出，所研制的配电网高精度PMU装置能够准确地表征配电线路电压沿线下降的特性，且测量精度足以区分出短线路的相位差，显示了其高精度测量性能。

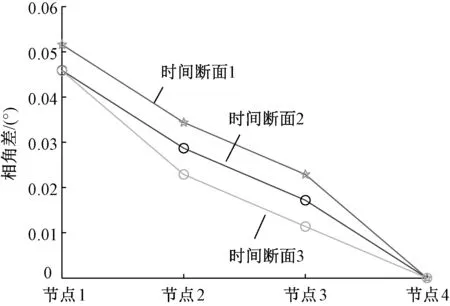
图10 某10 kV线路沿线电压相位关系

6 结论

根据配电网同步相量测量的应用背景和特殊要求，提出了一种兼顾测量精度和动态响应性能新型配电网同步相量算法。在实际配电网PMU装置中实现了该算法并在实际配电系统中应用。根据实测数据可以发现，实际配电系统中具有较高含量的谐波与间谐波。由于负荷的波动性，电压产生频繁的波动。同时由实测数据可知，本文所提算法在实际运行中保持了良好的稳定性与优秀的准确性。对算法在标准场景及配电网实际测量环境下的性能进行了全面的测试，验证了本文所设计算法的高精度和快响应特性。