基于改进LMD方法的风电机组齿轮箱故障诊断研究
李 辉,邓 奇
(西安理工大学电气工程学院,陕西 西安 710048)
0 引言
近年来,由于全球环境恶化和资源短缺,使得世界各国逐渐开始重视开发和利用可再生能源。其中,风力发电已逐渐成为可再生能源活跃的热点。齿轮箱作为风电机组的核心零部件之一,由于其特殊的工作环境,较易发生故障,且一旦出现故障必定造成巨大的经济损失[1-2]。因此,对风电机组齿轮箱进行故障诊断,对提高发电效率和节约成本具有十分重要的意义。
风电机组齿轮箱振动信号具有非线性和非平稳性等特点。针对非线性和非平稳信号,其分析常采用时频分析方法。常用的时频分析方法有经验模态分解(empirical mode decomposition,EMD)、小波变换、短时傅里叶变换、魏格纳威利分布。EMD是一种自适应的将信号分解为多个固有模态分量(intrinsic mode component,IMF)的方法。但EMD存在严重的端点效应和模态混叠问题。小波变换方法虽然对线性信号的处理比较好,但不适用于非线性和非平稳信号。短时傅里叶变换、魏格纳威利分布虽能在一定程度上描述信号的瞬时频率分布,但都以傅里叶变换为基础,没有从根本上解决傅里叶变换的弊端。
局部均值分解[3](local mean decomposition,LMD)是由Jonathan S.Smith提出的一种新的自适应非平稳信号的处理方法。该方法将复杂的多分量调幅调频信号分解为单分量的调幅调频信号。其分解结果不仅能准确反映出信号的时频分布,且特别适合分析多分量非平稳信号[4]。程军圣等[5]将局部均值分解方法与反向传播(back propagation,BP)神经网络结合起来,并应用到滚动轴承故障诊断中。李慧梅等[6]提出基于 LMD 的边际谱的滚动轴承故障诊断方法。结果表明,该方法能够有效地提取滚动轴承的特征频率。胡劲松等[7]将三次样条插值过程引入LMD,用于计算局部均值函数和包络估计函数,使LMD算法的计算效率和精度都有了一定的提升。虽然LMD在EMD的基础上作了改进,但LMD依然存在模态混叠现象,使得分解结果产生偏差,最终影响故障诊断的准确性。
为了减少由于求取局部均值函数带来的误差。本文提出了一种基于局部积分均值的LMD改进算法,并成功应用于风电机组齿轮箱故障诊断中。
1 工作原理
1.1 LMD原理
LMD将原始信号分解为一系列PF分量与一个残余项的和,每个PF分量可以看作是一个包络信号和一个纯调频信号的乘积,具体的算法步骤如下。
①对于一个原始信号x(t),找出全部极值点ni,并求出相邻两个极值点之间的局部均值mi和局部包络ai。
(1)
(2)
②将所有的局部均值mi和局部包络ai在其对应的极值点时刻tni和tni+1之间进行直线延伸,再采用滑动平均法进行平滑处理,得到局部均值函数m11(t)和局部包络估计函数a11(t)。
③将局部均值函数m11(t)从原始信号中分离出来,得到零均值信号h11(t)。
h11(t)=x(t)-m11(t)
(3)
④对h11(t)进行解调,得到s11(t)
(4)
重复上述步骤①~步骤②,可以得到有关s11(t)的局部包络估计函数a12(t)。若a12(t)=1,则证明s11(t)为纯调频函数;若a12(t)≠1,则需要重复上述迭代,直到式(5)成立,此时s1n(t)是一个纯调频信号。
a1(n+1)(t)=1
(5)
⑤将迭代过程中所产生的全部局部包络估计函数相乘得到包络信号a1(t)。
(6)
⑥原始信号的第1个PF分量为MPF1:
MPF1=a1(t)s1n(t)
(7)
原始信号的幅值为a1(t),根据调频信号s1n(t)可以得到瞬时频率为f1(t)。
(8)
⑦ 将MPF1从原始信号中分离出来,得到u1(t);将u1(t)作为原始信号重复步骤①~步骤⑥、循环k次,直到u1(t)成为一个单调函数为止。
原始信号x(t)被分解为k个PF分量和一个单调信号uk之和,即:
(9)
1.2 改进的局部均值分解
本节将改变以往采用平均值的方法求取局部均值函数,改用局部积分均值方法求取局部均值函数。具体步骤如下。
①找出原始信号中的所有极大值和极小值点,将其按顺序排列构成(tk,xk)。
(10)
2 特征向量的提取
多尺度熵(multiscale sample entropy,MSE)是Costa在2005年提出的理论[6-8],是在样本熵的基础上引入尺度因子,表述时间序列在粗粒化下的样本熵趋势,从而分析信号在不同尺度因子下的复杂程度和自相似性。多尺度熵的具体步骤如下所示。
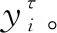
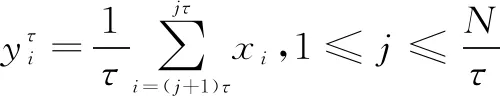
(18)
②根据尺度因子τ,考虑m维矢量Yτ(i),表示在尺度因子τ下的m个连续yτ值,其中m为嵌入维数。
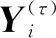
(19)
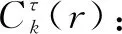
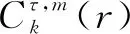
(20)
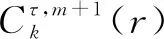
⑦对于一个长度为N的原始时间序列Xi,其样本熵值为:
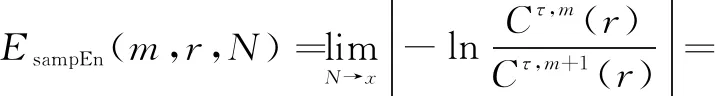
(21)
影响多尺度熵计算精度的参数有尺度因子τ、相似容限r、嵌入维数m和信号长度N。一般情况下,取r=0.1~0.25SD(SD为原始时间信号的标准差),m=2,τ=20,N需足够大。本文取r=0.2SD,N=2 048。
将多尺度熵作为信号的特征,得到一个反映故障信息的特征向量T,即:
T={CMSE1,CMSE2,…,CMSEτ}
3 极限学习机
极限学习机[9](extreme learning machine,ELM)是一种针对单隐含层前馈神经网络算法。其最突出的特点是学习速度快、泛化能力强、参数设定简单等。
假设有Q个带标签的数据样本(Xh,Yh)。其中,1≤h≤Q,Xh=[xh1,xh2,…,xhs]T∈Rs为第h个输入样本,Yh=[yh1,yh2,…,yhs]T∈Rr为与之对应的目标输出,s为输入样本的维数。若单隐含层前馈神经网络中输入层、隐含层和输出层的单元数分别为s、l、r,则该网络的输出可表示为:
式中:g为激活函数;Wc为输入权值;bc为第c个隐含层单元对应的偏置;βc为输出权值;Oh为第h个样本对应的输出。
ELM网络训练的目标是使得输出误差最小化,因此定义训练样本的最小损失函数为:
式中:H为隐含层单元的输出矩阵;β为输出权值矩阵;Y为样本目标输出矩阵。
当激活函数无限可微时,单隐含层前馈神经网络的参数不必全部调整,Wc和bc可随机初始化并在训练中保持不变,而输出权值矩阵β可通过式(22)的最小二乘解得到。
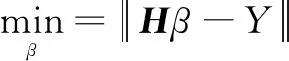
(22)
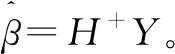
4 故障诊断
为了解决LMD在故障诊断中识别精度不高的问题,本文采用改进的LMD进行故障诊断。其具体步骤如下。
①信号采集。利用振动传感器采集风电机组齿轮箱的故障信号。
②LMD分解。采用改进的LMD对信号进行分解,得到n个PF分量。
③计算互相关系数。计算每个PF分量和原始信号的互相关系数。
④重构信号。将互相关系数大于0.3的PF分量进行重构。
⑤将重构信号的多尺度熵作为特征向量T。
⑥构建极限学习机故障诊断模型。用构建的训练样本集进行训练,得到最终的极限学习机故障诊断模型。
⑦故障识别。将构建的测试样本集输入到分类器中,实现风电机组齿轮箱故障识别。
5 仿真分析和试验验证
5.1 仿真分析
为了验证改进局部均值分解能有效抑制模态混叠现象,采用AM-FM信号进行仿真分析。该仿真信号由调幅频率为5 Hz,基频为60 Hz,调频频率为8 Hz的AM-FM信号和调幅频率为10 Hz的正弦信号构成,其表达式为:
LMD分解如图1所示。
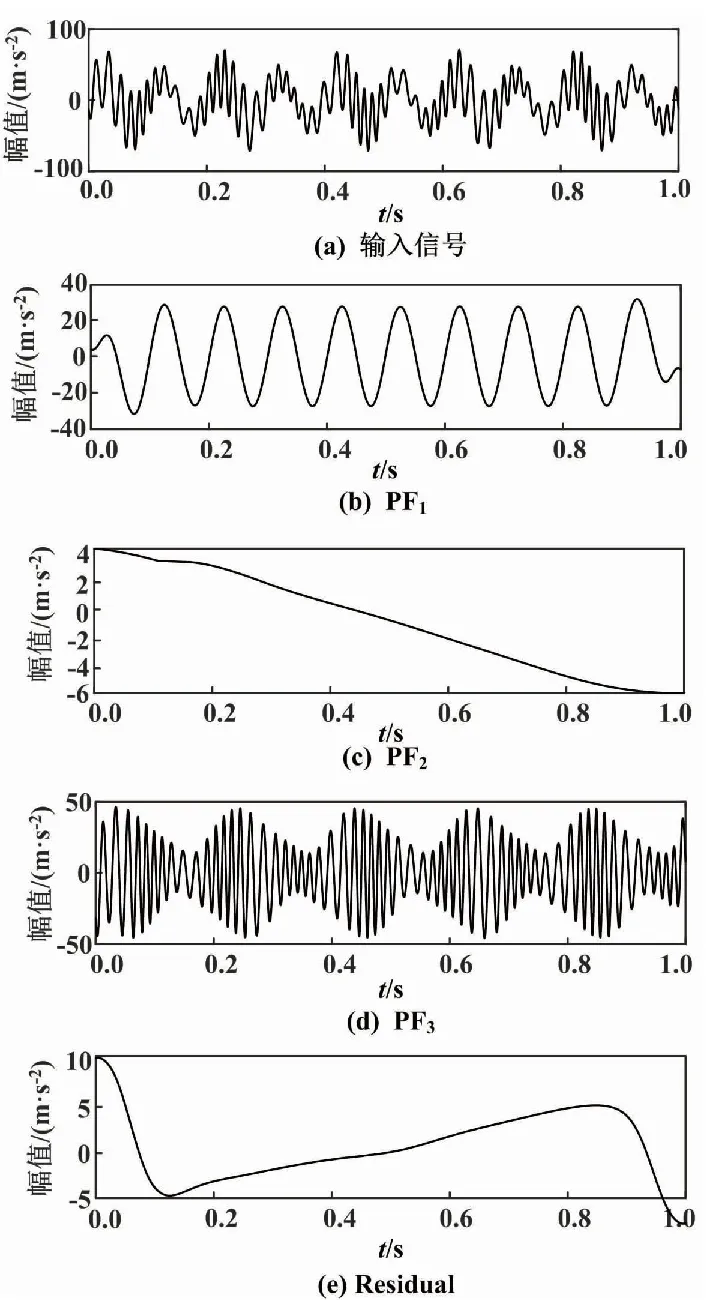
图1 LMD分解图
由LMD分解时域图可知,采用LMD分解将仿真信号错误地分解为3个PF分量。由PF1包络频谱图可以看出,PF1中出现模态混叠现象,在50 Hz左右两端出现了干扰信号。
改进LMD分解如图2所示。采用改进LMD将信号准确的分解为2个PF分量。由PF1包络频谱图可知,PF1中未出现模态混叠现象。通过对比分析,证明了改进LMD方法能有效地抑制模态混叠现象,分解结果更准确。
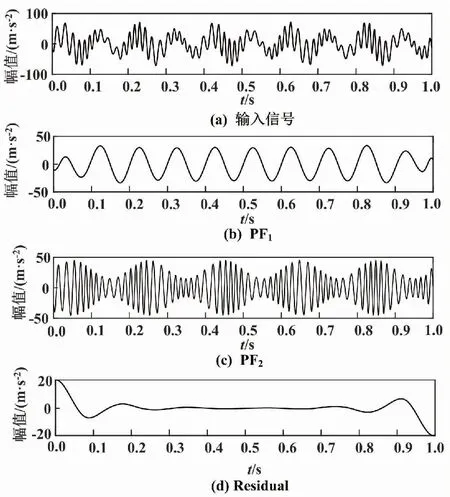
图2 改进LMD分解图
5.2 试验验证
本文选用美国凯斯西储大学电气工程试验室提供的滚动轴承试验数据进行分析;采用6205-2RS JEM SKF型深沟球轴承;选用滚动轴承驱动端的故障数据进行分析,其采样频率为12 kHz。以转速为1 797 r/min、信号长度为1 024的滚动轴承内圈故障为例进行分析,由式(25)计算得到实际故障频率为162.185 2 Hz。
(25)
式中:fr为滚动轴承内圈旋转频率;dw=0.312 6 mm为滚动体直径;zw=9为滚珠个数;Dq=1.537 mm为轴承节径;α=0为滚动体接触角。
分别采用LMD和改进LMD方法对滚动轴承内圈故障信号进行分解。LMD分解时域如图3所示。改进LMD分解时域如图4所示。

图3 LMD分解时域图

图4 改进LMD分解时域图
包络频谱如图5所示。
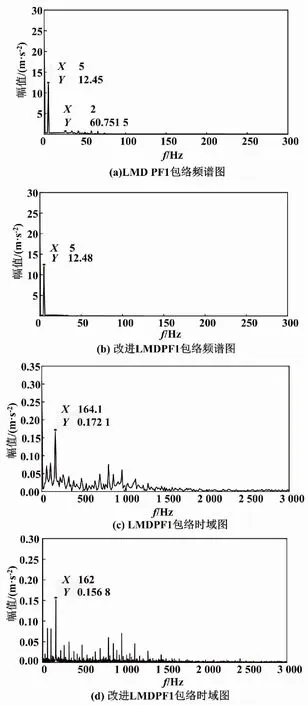
图5 包络频谱图
由图5可知,故障信号的特征频率为164.1 Hz,相比实际特征频率大了1.914 8 Hz。从包络频谱图可以得出,故障信号的特征频率为162 Hz,相比实际特征频率减小了0.185 2 Hz,与滚动轴承内圈故障特征频率基本相同。通过对比采用LMD和改进LMD方法对滚动轴承内圈故障进行分解,结果表明改进LMD方法的分解结果更准确。
5.3 故障诊断
选取内圈故障、外圈故障、滚珠故障及正常四种故障数据共200组,每组样本长度为2 048。其中,140组样本作为训练样本,其余60组样本进行分类正确率验证。对四种故障状态设置相应的标签,c=[1,2,3,4]。
首先分别采用LMD和改进LMD方法对信号进行分解,然后求取各PF分量和原始信号的互相关系数,剔除互相关系数小于0.3的分量,对剩余PF分量进行重构,求取重构信号的多尺度熵值,将ELM作为分类器对滚动轴承进行模式识别。LMD分类结果如图6所示。
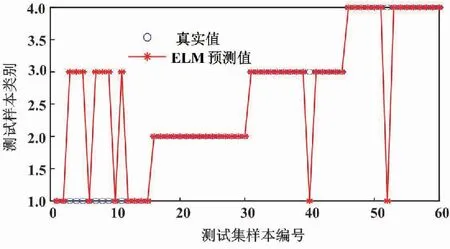
图6 LMD分类结果
由图6可知,采用LMD进行预处理后,分类结果中有7组内圈故障、1组滚珠故障和1组正常出现误诊断,最终识别的准确率为85%。改进LMD分类结果如图7所示。
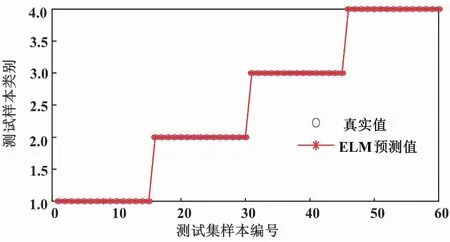
图7 改进LMD分类结果
由图7可知,采用改进LMD进行预处理后,所有故障均被正确分类,最终识别的准确率为100%。通过对比采用改进LMD分解方法和LMD分解方法可得,采用改进LMD方法分解最终故障识别的准确率更高。
为了进一步说明本文所提方法的有效性,将本文改进的局部均值分解和极限学习机的故障诊断方法与支持向量机(support vector machine,SVM)、最小二乘支持向量机(least squares support vector machine,LSSVM)的故障诊断方法进行比较,采用同一数据进行模式识别。故障诊断结果对比如表1所示。

表1 故障诊断结果对比
上述分析可得,本文所提的基于改进的LMD和极限学习机的故障诊断效果明显好于其他2种故障诊断方法,充分说明了本文方法能提高故障诊断的识别精度。
6 结论
本文针对LMD方法中存在模态混叠问题,提出了基于局部积分均值的LMD改进算法。通过仿真分析验证了本文所提方法能够精准地对仿真信号进行分解,并有效地抑制了模态混叠现象。将本文所提的改进LMD方法应用到风电机组齿轮箱故障诊断中,通过多尺度熵准确提取出故障信号的特征向量,最后采用极限学习机进行故障诊断。通过仿真分析,证明了本文所提方法优于其他方法,为风电机组的可靠运行提供了可靠保障。

