基于低秩模型的电力能源大数据异常修正方法研究

马草原

(国网天津市电力公司,天津 300000)

0 引言

电力系统含有庞大的实时数据。这些数据与电力系统的安全运行有着密切联系，对电力系统的安全与可靠起到决定性作用。电力系统工作过程中需要产生和消耗大量电力能源，在正常工作的情况下依然会产生不良数据影响系统的决策，威胁整个电力系统的安全[1-3]。因此，利用专业技术检测出不良数据并修正，有助于保证电力系统的正常运行和电力能源的正常供给。

到目前为止，国内外学者对电力能源大数据的检测和修正作了很多理论与实际研究，总结出两种使用比较广泛的修正方法。一种是基于Spark框架的电网运行异常数据辨识与修正方法，通过聚类或神经网络等数据挖掘算法在大数据中提取出异常数据，在Spark框架下对其进行修正[4]。另一种是基于改进低秩矩阵补全的电网数据缺失值修正方法。这种方法主要根据一定的置信度水平设置阈值，结合概率论相关知识进行假设检验，然后通过改进低秩矩阵补全数据缺失值，实现异常修正[5]。

以上两种方法中存在因过多重复的搜索次数导致数据辨识异常，或将正常数据误判为不良数据的情况。针对这种情况，设计基于低秩模型的电力能源大数据异常修正方法，解决以往修正方法中存在的问题。

1 方法设计

1.1 基于低秩模型的电力能源数据处理

利用低秩模型，在电力能源大数据中去除噪声数据，分离出含有有利信息的数据[6]。低秩的一般表示形式如下：

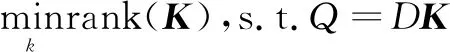
(1)

式中：K为系数矩阵；Q为电力能源数据样本；D为字典[7-8]。

假设在一个时间序列中得到的所有数据将形成一个矩阵，表示为W。设定w为状态量、A为异常数据矩阵，具有不稳定性和离散特性。在时间序列内，电力能源正常数据呈连续平稳的特征[9-11]。根据上述特征确定初步的目标方程为：

(2)

式中：η为平衡参数，η>0；rank(K)为矩阵K的秩；sparse(A)为矩阵A的一个稀疏约束。

在实际应用中，将D初始化，作为矩阵稀疏约束实例化的范数，计算出目标方程的最小解，也就是低秩模型中最小化矩阵的秩[12-13]。综上，式(2)可进一步写为：

(3)

将式(3)作为低秩模型监测异常数据。为了更好地处理电力能源大数据中的异常数据，根据实际需求，将初始化后的D分为两个部分，一部分用来观察关键量测量数据，另一部分用来观察非关键量测量的异常数据。即：

D=[D1,D2]

(4)

式中：D1为用于表达观测到的模式；D2为隐藏的潜在模式。

考虑低秩模型中：正常电力能源数据与异常电力能源行为均遵循一定规则；异常数据并不只是胡乱地零散分布，而是表现出一定特征。在处理噪声数据中，引入特征选择方法深度挖掘噪声信息，则最终的目标方程如下所示：

(5)

式中：D1和D2为在已知情况下得到的已划分数据样本。

利用目标方程不断更新数据样本，并以数据样本的收敛性作为判断更新次数是否达到最大的条件。若达到最大更新次数，则停止更新。此时的电力能源数据已满足检测辨识和修正对数据的要求。通过上述过程，得到不含噪声的电力能源大数据样本。

1.2 辨识电力能源数据

通过低秩模型得到有规律的电力能源数据，考虑大数据中异常数据的特性，将支持向量机(support vector machine,SVM)作为辨识数据的主要工具，在离线模式和联机模式下辨识出异常数据。

异常数据与正常数据的区别与数据有功功率和时间的比值相关，计算出某一数据点与该点相邻点的有功功率和时间的比值。若比值的绝对值大于正常运行状态下的正常比值，则说明该点数据为异常数据。SVM作为典型的二分类模型，存在训练和应用两个阶段。采用离线模式训练SVM，训练数据来自电力能源数据库，对数据进行归一化处理：

(6)

式中:pi为数据库中第i个数据;pmin为数据库中的最小值;pmax为数据库中的最大值;p′i为归一化后的数据库中的第i个数据。

将归一化数据结果作为样本数据，并对样本数据进行分块处理，确保每一个样本块内部数据大小基本相同。通过聚类方法处理每个样本块中的数据集，获得对应的聚类结果，并将聚类结果整合。将上述结果看作一个完整聚类集，通过二次聚类后获得最终的聚类结果。聚类矩阵演变过程如图1所示。

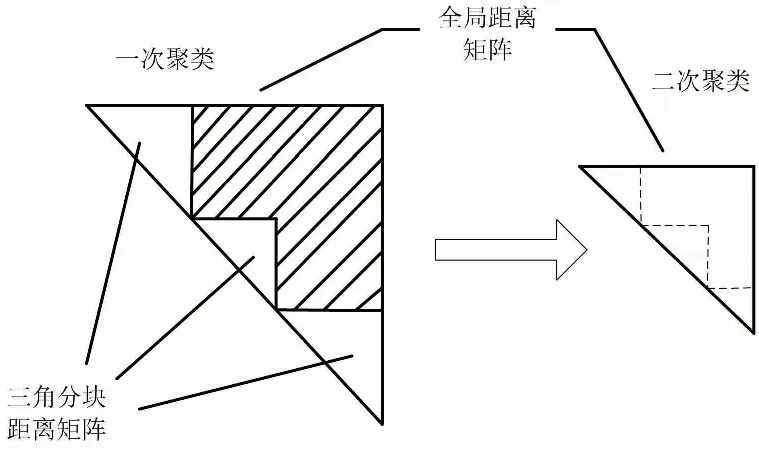
图1 聚类矩阵演变过程

对于每一次聚类，记录类簇包含的所有样本信息，计算类簇中心矢量：

(7)

式中:n为类簇包含的样本数;i为聚类次数;gi为样本i对应的数据矢量;gc为类簇中心矢量。

当聚类完成后，设置阈值ξ。当某个类簇中的数据个数小于设置的阈值时，将该类簇中的数据丢弃。剩下的数据就是具有一定的价值的数据。对于剩余的簇，采用针对性的训练措施，获得与簇一一对应的支持向量机模型。

针对剩余的类簇，计算出每个数据点对应的有功功率和时间的比值。对于时间起点和时间终点上的取值，对应的点取前一天或后一天的相邻值，数据点有功功率和时间的比值计算完成后，标记计算得到的每个数据特征，完成数据样本训练。

在各类簇聚类中心对应的数据经过归一化处理之后，计算聚类中心与对应的时段数据的距离，对比距离的大小并排序，使用与最小距离的类簇数据对应的支持向量机模型，对类簇数据一一分类，得到初步数据辨识结果。在分类完成后，设置一个滑动窗口，接收待处理某一时段电力能源数据。滑动窗口的大小由该时段数据个数确定。当滑动窗口接收数据操作完成后，在类簇中寻找距离最近的时段数据，使用与其对应的支持向量机模型简单辨识出异常数据。

假设辨识出的时段数据中异常数据的点数为m，默认此时的滑动出窗口边界处的数据均为正常数据。在此条件下，当时段数据中异常数据的点数小于3时，修正异常数据；当时段数据中异常数据的点数大于等于3时，修正除时间起点和时间终点的所有异常数据。对于时间起点和时间终点的数据，计算其特征值，重新辨识该数据。在重新辨识过程中，如果滑动窗口的上边界处为异常数据的同时上一窗口未关闭，则时段数据中异常数据点数的计算不仅需要结合当前窗口，还需要将上一窗口的时段数据计算在内。

通过上述过程辨识出电力能源大数据异常数据，电力能源大数据的修正随着窗口上界和下界的变化进行。

1.3 修正电力能源异常数据

根据基尔霍夫电流定律可知，在电力能源产生和供给过程中，如产生的数据都是正常数据，则有功功率和无功功率互相抵消，相加的总和为零。此时，节点的功率是平衡的。假设母线上有b条支路，第j条支路的有功功率和无功功率分别为Pj和Uj，则节点功率平衡的表达式如下：

(8)

(9)

当线路某侧有功确定为正常数据时，则根据式(8)、式(9)修正另一侧异常数据：

(10)

(11)

式中:v为b条支路中第v条支路。

若线路两侧均为异常数据，则令与待修正数据点首尾相邻的点为(x0,y0)、(x1,y1)，待修正点为(x,y)，根据以下公式修正：

(12)

式中:ε为修正系数。

通过以上方法修正异常数据，适用于单个或多个不相关的异常数据的修正，并且能够实现零误差的修正。至此，基于低秩模型的电力能源大数据异常修正方法设计完成。

2 试验

2.1 仿真数据及数据预处理

利用IEEE-30节点系统的数据作为试验数据，归一化处理遥感数据。IEEE-30节点电网接线图2所示。

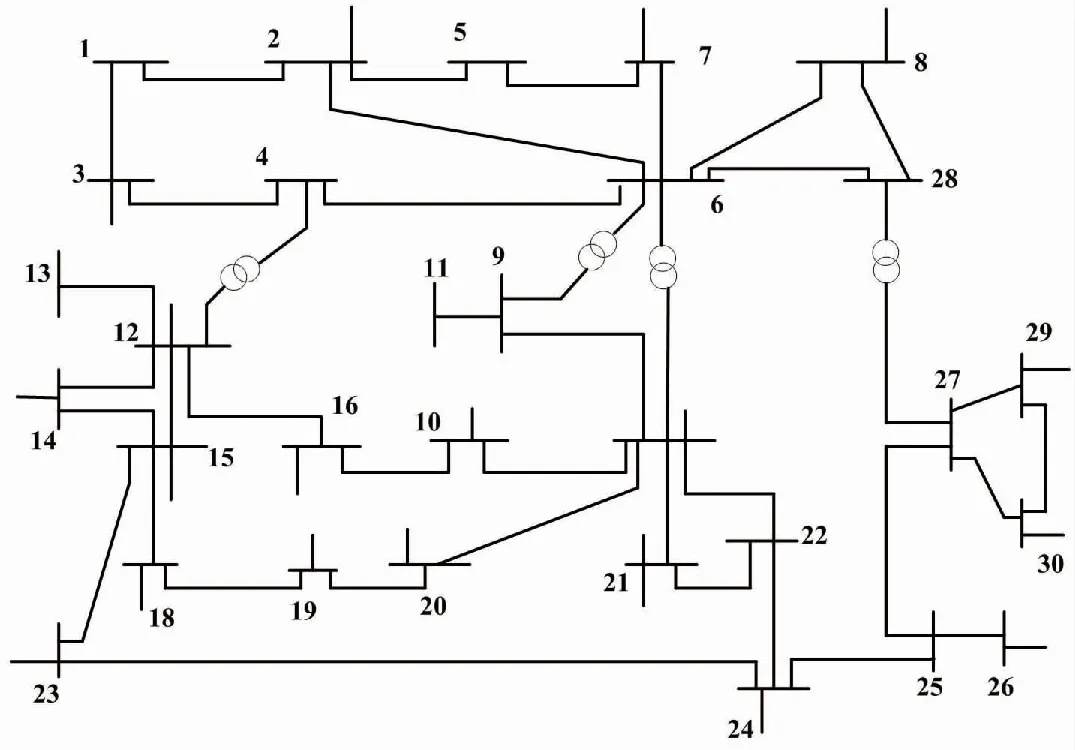
图2 IEEE-30节点电网接线图

采用IEEE-30节点的大型电网数据进行仿真。量测数据主要包括节点注入的有功和无功功率，支路潮流的有功和无功功率。IEEE-30节点量测配置如表1所示。

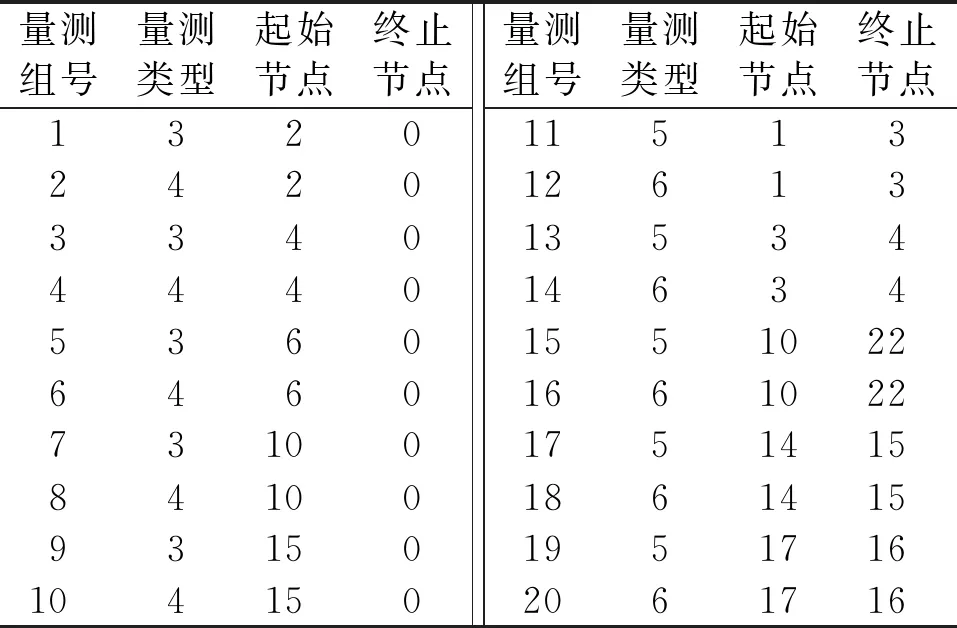
表1 IEEE-30节点量测配置表

使用不同的电力能源大数据异常修正方法处理量测数据。在量测数据过程中，对组号为3、7、9、15、19的测量节点设置30%的量测误差值，将其作为异常数据用于后续试验中，验证不同的电力能源大数据异常修正方法对异常数据的辨识情况。基于辨识结果，计算不同修正方法的残差值。

2.2 负荷数据异常修正结果及分析

使用不同的电力能源大数据异常修正方法，分别对量测数据进行检测与修正。通过仿真验证不同修正方法的负荷数据异常修正效果。电力负荷数据异常修正结果如图3所示。

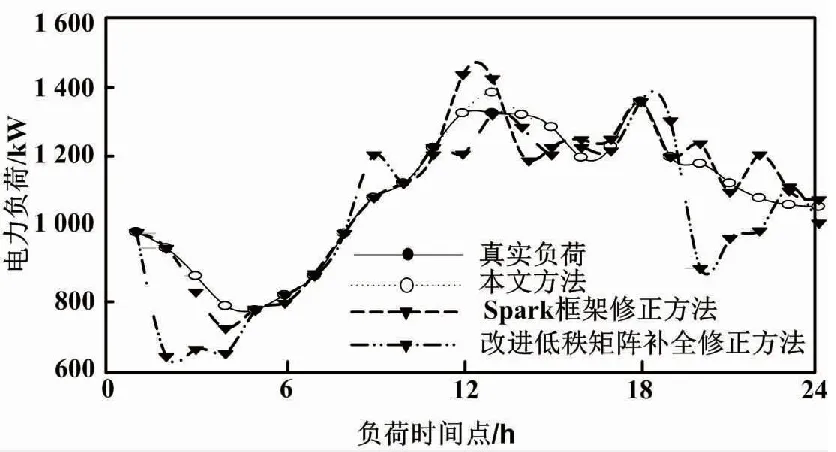
图3 电力负荷数据异常修正效果

分析图3可知，不同方法下电力负荷数据异常修正效果不同。对于不同时间点来说，电力负荷会发生一定的改变，整体来看，电力负荷先下降后上升再下降。中午12 h时，电力负荷最大。此时电力系统实际负荷为1 325 kW，Spark框架修正方法的电力负荷为1 432 kW，改进低秩矩阵补全修正方法的电力负荷为1 213 kW，本文方法的电力负荷为1 325 kW。经过本文方法修正后，电力负荷与实际负荷值相符。而Spark框架修正方法与改进低秩矩阵补全修正方法的修正效果不理想。经过本文方法修正后的曲线与实际负荷曲线基本重合，而其他方法的负荷曲线明显存在一定差异。这说明本文方法电力负荷数据异常修正效果最好。这是因为本文方法能够对不同模式采用不同的方法实现误差修正，并且通过滑动窗口获得异常数据，使修正准确性得到提升。

2.3 残差值试验结果及分析

残差表示观察值与拟合值之间的差值，可作为误差的观测值。残差值越小表示误差越小，说明修正的效果效果越好。为此，本文通过残差值判断不同方法法修正效果。使用不同的电力能源大数据异常修正方法处理，获得不同方法在各个量测组的残差值。不同方法的残差值如表2所示。

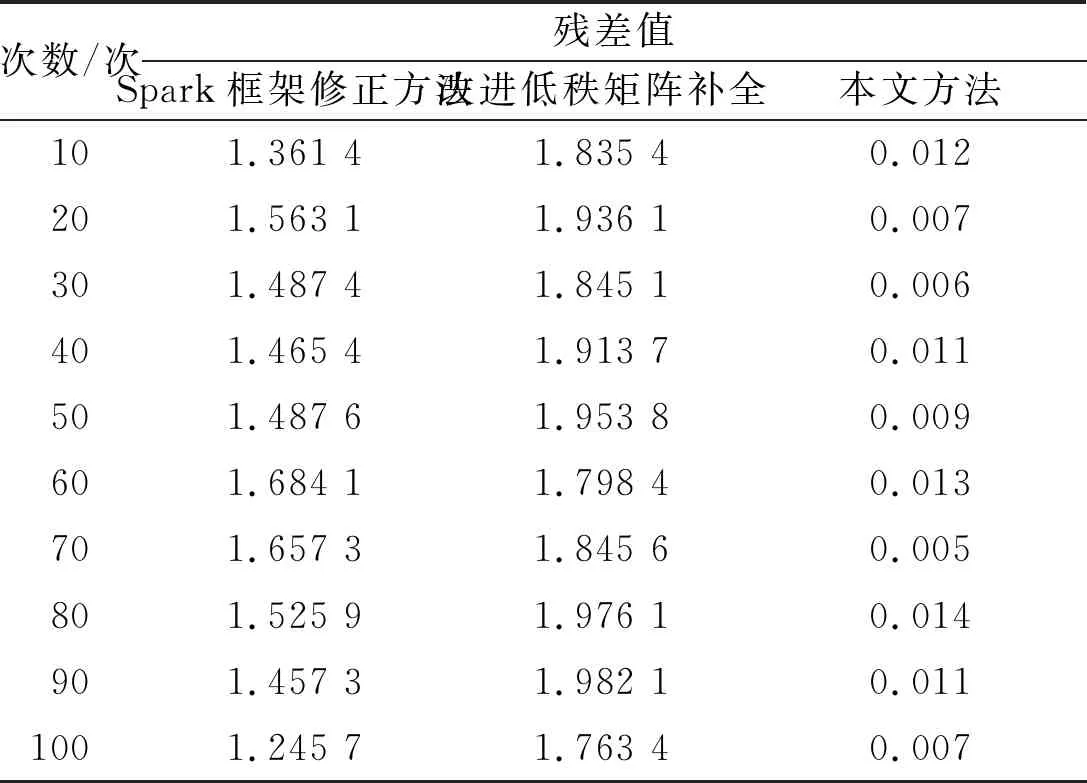
表2 不同方法的残差值

分析表2可知，不同方法的残差值不同。当试验次数为10次时，Spark框架修正方法的残差值为1.361 4，改进低秩矩阵补全的残差值1.835 4，本文方法的残差值0.012，本文方法的残差值为最低。整体来看，Spark框架修正方法的平均残差值为1.493 52，改进低秩矩阵补全的平均残差值为1.884 97，本文方法的平均残差值为0.009 5。本文方法的残差值最低，说明本文方法具有较为准确的电力能源大数据异常修正结果。这是因为本文方法采用了低秩模型对电力能源数据样本进行去噪处理，去除了样本噪声，提高了数据结果准确性。

3 结论

随着电力输电系统进入超高压远距离输电、跨区域联网的新阶段，在电力能源大数据中产生了很多异常问题。本文针对这一问题，设计基于低秩模型的电力能源大数据异常修正方法，利用低秩模型展开了一系列的研究。通过与以往使用的修正方法对比试验，验证了设计的修正方法在处理电力能源大数据时具有很好的性能，实用性强，简单易行。