基于自动聚焦技术的三维测量方法研究

刘 斌，赵 静 ，谯 倩 ，李志伟 ，朱均超 ，许 亮 ，张宝峰

(1.天津市复杂系统控制理论及应用重点试验室，天津 300384；2.天津理工大学电气电子工程学院，天津 300384)

0 引言

微结构三维测量的方法主要分为接触式测量和非接触式测量。接触式测量使用探针对被测物表面进行扫描。三坐标测量机(coordinate measuring machine,CMM)是一种常见的接触式测量仪。接触式测量[1]可以获得清晰的被测物表面形状轮廓，完成较长距离的测量。但被测物表面会因探针的碰触而留下瑕疵，无法测量比探针端半径还要小的沟槽。目前，非接触式测量的常用方法有白光干涉法[2]、双目法[3]、激光三角法[4]、光度法、结构光法[5]、聚焦法等。聚焦法[6]利用图像清晰度评价函数判定聚焦最清晰位置，进而获得深度信息，适合测量范围较小的物体。其精度较高且成本低，但易受光照不均等因素影响。

实现微小物体表面轮廓的非接触测量，其关键问题在于如何精确获取表面轮廓的深度信息。针对这个问题，提出了改进的聚焦判定方法，对图像的清晰度评价算法进行了优化。

1 系统与测量方法

基于自动聚焦技术的三维测量系统由工业摄像机、环形光源、高精度三维位移台、计算机组成。系统测量过程示意图如图1所示。

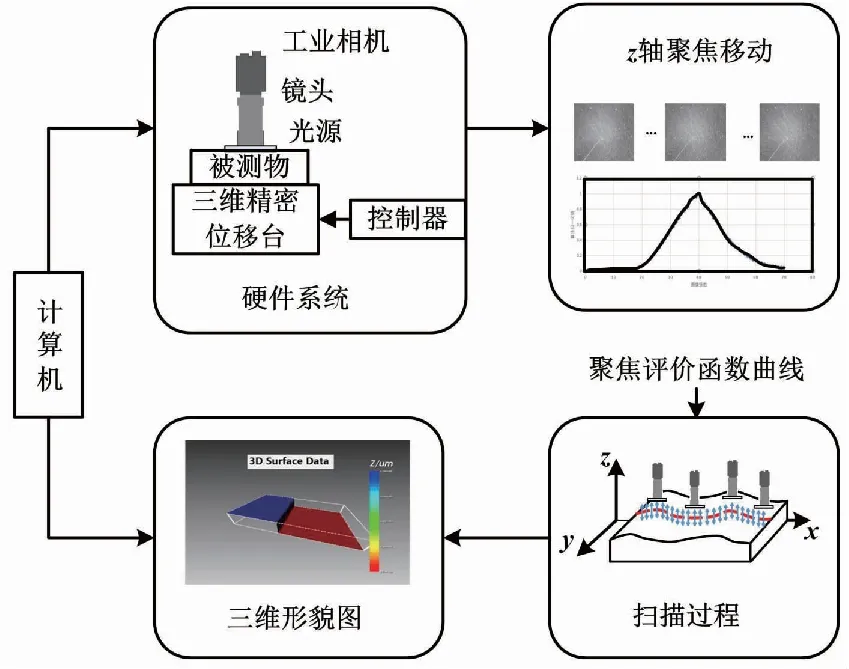
图1 系统测量过程示意图

测量流程如下。

①探头由工业相机、光学镜头和光源组成，搭载于三维平移台装置上。环形光源将被测物照亮，工业摄像机拍摄被照亮的被测物，计算机可通过控制高精度电动三维位移台，对被测物表面进行垂直扫描，采集图像序列。

②工业相机的作用类似于接触式测量法中的探针，但以基于图像的聚焦判定代替了传统的力接触，实现非接触的轮廓点测量。其所采集的图像数据通过数据线传输至计算机，对图像序列进行清晰度评价计算，从而可确定最清晰图像所在位置，进而获取该点深度方向的z值坐标。

③当位移台载着被测物沿x轴与y轴移动，可完成表面轮廓的形貌测量，最终形成三维点云数据。

通过该方法获取被测表面点的深度信息依赖于图像清晰度评价的聚焦判定。要保证系统的深度尺寸测量精度就需要单峰、灵敏、无偏、鲁棒的聚焦判定方法。常用的聚焦判定算法有Tenengrad算法[7]、Brenner算法[8]、ImprovedBre算法[9]、AbsVar算法[10]、Roberts算法[11]、Laplacian算法[12]、Autocorrection算法[13]、Entropy算法[14]。

但在实际测量过程中，由于环境光与被测表面的反射特性，容易造成光照不均现象。同时，电荷耦合器件(charge coupled device,CCD)相机信号转换的噪声等也会一定程度降低图像质量，产生图像细节信息被掩盖的情况，易导致常用算法失去稳定性。

本系统采集的标准量块表面采集图像如图2所示。

图2 标准量块表面采集图像

2 改进的聚焦判定方法

为保证系统测量精度，需要对图像进行预处理，弥补光照不均，增强图像细节信息，为基于图像清晰度的聚焦判定提供高质量图像数据。

常用的图像增强算法有对数法[15]、指数法[16]、直方图法[17]、高反差保留法[18]、Retinex算法[19]。其中Retinex图像增强算法基于照度反射模型，对光照分量进行估计，可有效弥补光照损失。基于Retinex理论，相机采集到的图像由入射光分量和物体的反射分量构成。相机所采集到的图像I(x,y)可以理解为是被测物的反射分量R(x,y)与入射光分量L(x,y)相乘的结果。该过程可由式(1)表示：

I(x,y)=R(x,y)L(x,y)

(1)

颜色恒常性理论认为物体的反射分量反应了物体的本质信息，Retinex算法利用数学方法去除图像中的光照部分，得到物体的反射分量[20-22]。

将式(1)进行对数变换，得到：

log[R(x,y)]=log[I(x,y)]-log[L(x,y)]

(2)

式中:光照分量L(x,y)是从原图像提取的光照近似融合图像。

对基于Retinex算法的原理进行了研究，实现了改进算法。将图像中的低频和高频信息分别处理、提取，再进行融合，进而与图像清晰度判定函数结合，形成了改进的聚焦评价方法。

相机采集到的图像中，光照分量变化缓慢的部分表现为频域的低频分量，因此，采用合适的低通滤波器可以近似估计出图像的光照信息。采用的CCD相机采集的图像是由(2 048×2 048)个像素点构成的，选取均值滤波器提取图像光照近似信息。该滤波器是由方框滤波归一化后的一种特殊情况，属于线性滤波的一种，是将当前像素点(x,y)的灰度值由模板中各个像素点的平均灰度值代替，即：

(3)

较小的模板滤波器的滤波效果还保留着图像的大致轮廓，较大模板滤波器的滤波效果较好地模拟出了图像的光照信息。因此，采用(495×495)像素大小的模板来对原图像I(x,y)进行滤波平滑，估计近似光照信息i(x,y)。滤波模板M如下：

(4)

随着位移台载着被测物作垂直运动，相机与被测物之间的距离随之变化，采集到的图像由不清晰到清晰再到不清晰。采用canny算子提取原图像集中每幅图像的边缘细节g(x,y)，每幅图像canny算子中的参数k计算如下：

k=1-(0.8×ε)

(5)

式中:ε为每幅图像归一化后的梯度值。

采用Tenengrad算法求得图像梯度值：

D(x,y)=∑y∑X|G(x,y)|,G(x,y)>T

(6)

T为设定好的边缘检测阈值，G(x,y)的形式如下：

(7)

GX和Gy分别为点(x,y)基于Sobel算子水平和垂直方向的卷积。

搜索边缘细节图g(x,y)中灰度值为255的像素点，找到近似光照信息图像i(x,y)中相应位置。将该像素点的灰度值设为i(x,y)的平均值，生成融合了光照近似信息和边缘细节的融合图像L(x,y)，代入式(2)可求得反射分量R(x,y)。

改进的聚焦判定方法流程如下。首先，对图像进行高低频信息提取，获取低频信息作为图像光照近似信息、高频信息作为图像边缘细节信息。然后，将高、低频图像进行图像融合。随后，对融合后的图像用Retinex算法进行图像增强处理。最后，采用Tenengrad梯度函数对图像进行清晰度计算。改进的聚焦判定方法流程如图3所示。

图3 改进的聚焦判定方法流程图

3 试验结果与分析

由CCD工业相机、镜头和环形光源构成图像采集系统。位移台系统为电动三维位移台，其位移重复性精度小于3 μm。将被测物放置在平移系统上，完成扫描测量。

3.1 图像增强函数分析对比

采用改进的Retinex算法与其他常用方法对图2所示的原图进行图像增强处理，图像增强法对比如图4所示。

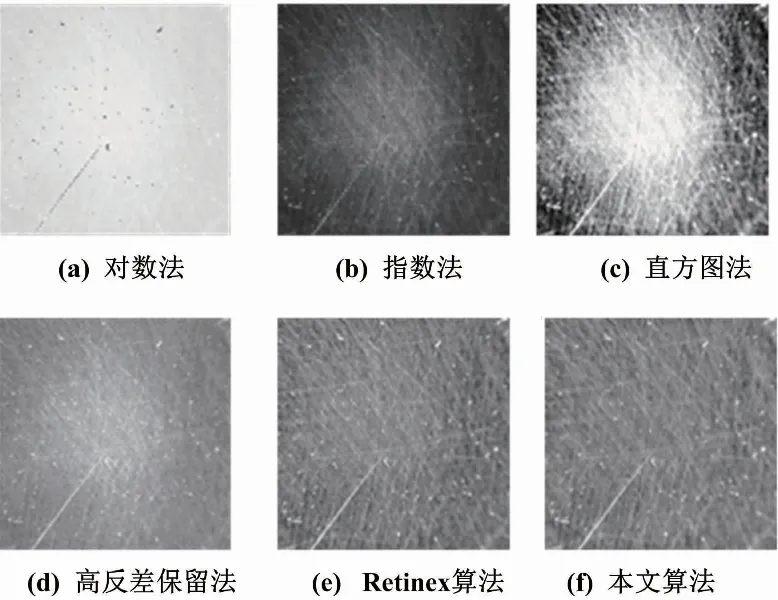
图4 图像增强法对比图

从图4可以看出，提出的改进算法能有效地在去除光照不匀影响的同时，保留了足够的图像细节信息，为之后图像清晰度评价提供了细节充足的图像。

3.2 聚焦判定方法分析对比

将本文提出的算法与其他常用算法对CCD相机采集到的70张图进行清晰度计算，每个算法的结果归一化处理后得到如图5所示的清晰度评价算法对比曲线图。

图5 清晰度评价算法对比曲线

AbsVar算法的单峰性和灵敏度不佳。Tenengrad算法、Brenner算法、ImprovedBre算法、Roberts算法与Laplacian算法在37到43张图之间，清晰度值已趋于平缓，灵敏度降低。采用的清晰度评价算法在该区域仍能有效判定最清晰的第40张图，比其他算法单峰性与无偏性更好，灵敏度更高。

3.3 系统测量试验与分析

采用由2 mm高度的标准量块与0.5 mm高度的标准量块组成1.5 mm高的台阶进行三维测量测试，计算台阶高度，并将结果与标准台阶理论高度进行对比。

对标准台阶表面进行扫描测量，点与点的距离为200 μm，在每个点上的垂直扫描步进为15 μm，X轴扫描范围为670～3 870 μm，Y轴扫描范围为-300～+300 μm。图6为台阶扫描范围示意图。

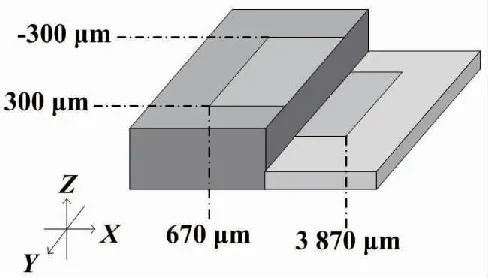
图6 台阶扫描范围示意图

标准台阶测量结果如图7所示。上表面测量44个点三维空间点，拟合平面为0.006 4x+0.039 9y-0.999 2z+2.240 6=0。下表面测量24个点三维空间点，拟合平面为0.003 4x+0.010 4y-0.999 9z+0.752 1=0。

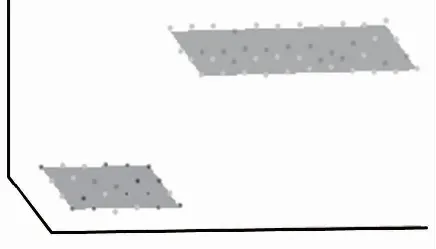
图7 标准台阶测量结果

计算每个下表面点到上表面拟合平面的距离，作为台阶高度测量值，评估系统的重复性测量精度。重复性验证试验数据如表1所示。

表1 重复性验证试验数据

试验数据表明，系统的平均偏差为0.007 mm，标准差为0.012 mm。

4 结论

本文提出了一种基于自动聚焦技术的三维测量方法，对标准量块进行垂直扫描。将所采集的图像序列通过数据线传输至计算机，将改进的Retinex算法与Tenengrad梯度函数相结合，对图像序列进行清晰度评价计算，实现聚焦评定，获取标准量块的深度信息。提出的改进聚焦判定算法，增强了图像的细节信息，提高了测量的适用性和稳定性。该方法的硬件系统成本低，并且可实现无接触测量。试验结果表明，该测量系统精度优于15 μm。