震后应急物资分配−运输问题研究

王小纯，牟海波

震后应急物资分配−运输问题研究

王小纯，牟海波

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

为实现震后应急物资的快速、公平分配，综合考虑应急物资需求数量的不确定性、灾区路网通行情况复杂、受灾点需求紧急度差异性、道路可分配车辆数有限、救援周期长等特点，采用机会约束规划方法，以各受灾点之间需求满足率之差最小、应急物资运达受灾点的时间最短和车辆运输与库存成本最低为目标，建立多时段应急物资分配-运输规划模型，并针对模型特点设计带精英策略的非支配排序遗传算法予以求解，通过算例验证了模型和算法的有效性。研究结果表明：可以得到有效的Pareto最优解，决策者可根据当期灾区的实际情况选择合适的物资分配-运输方案。

应急物资分配-运输优化；动态决策；模糊机会约束模型；非支配排序遗传算法

地震作为一种突发性和不确定性强的自然灾害，严重威胁着人类的生命财产安全。应急物资的分配方案和运输路线是应急救援过程中的关键一环，救灾物资的不合理分配会导致灾民无法得到有效的救助，不同的车辆运输方案也会影响救援时间和运输成本。因此研究震后应急物资分配−运输问题对提升救援效率具有重要意义。众多国内外学者从不同视角下研究了应急物资分配−运输问题。王妍妍等[1]考虑物资供给量、需求量和道路最大运输容量的模糊性特征，以延迟时间和损失最小化为目标，建立应急物资动态分配决策模型。付江月等[2]研究灾后首批救援物资分配问题，考虑需求动态变化特性，建立兼顾效率和公平的多目标整数非线性规划模型。王旭坪等[3]考虑震后灾民非理性攀比心理问题，建立救援物资分配模型。刘长石等[4]针对震后初期物资供不应求的现状，建立双层协同优化模型，顶层模型以分配公平最大为目标，底层模型以配送公平性和效率性最大为目标。李孟良等[5]研究震后救援物资多式联运问题，考虑需求、路网状况的不确定性，建立基于鲁棒优化的多式联运调配模型。陈则辉等[6]针对受灾段需求量、车辆行驶时间和成本的不确定性，建立模糊规划模型，并利用模糊数相关理论将其转化为确定型模型。田志强等[7]针对铁路突发事件的设备调度问题，建立以时间最短和费用最少的多目标优化模型，设计两阶段启发式算法求解。WANG等[8]引入非线性效用函数来量化公平，在此基础上建立多周期应急物资分配模型。ZHU等[9]研究了应急救援的路线选择、运输时刻选择以及灾害信息的更新，在此基础上建立救灾物资调度模型。Matl等[10]通过最小化各地救援投入差异来量化公平性。GUO等[11]针对海上搜救资源的分配问题，以应急物资利用率最大化和完成任务的可能性最大化为目标，建立整数非线性规划模型。Gutjahr等[12]讨论了剥夺成本的概念，并引用基尼不平等指数来量化物资分配的公平性。Cotes等[13]建立考虑设施选址的应急物资分配模型，目标是运输费用、库存费用、设施的固定费用和剥夺费用总和最低。CHEN等[14]针对多集散点、多受灾点的应急物资分配问题，建立双层整数规划模型，上层目标是加权配送时间最小，下层目标是物资分配公平性最大。综上所述，已有研究成果针对应急物资分配-运输问题，考虑到灾民的非理性攀比心理，采用物资需求满足率来量化公平，但受灾点需求紧急程度以及物资的效用性，对物资分配的公平性也会产生较大的影响，相关文献研究不多。因此，本文在既有研究的基础之上，针对应急物资短缺的现实情况，将受灾点需求紧急程度和物资效用影响因素引入公平性和时效性目标，基于应急物资配送的公平性、时效性和经济性要求，建立多集散点、多受灾点、多资源、多时段的应急物资分配−运输规划模型，针对此模型特点设计带精英策略的非支配排序遗传算法予以求解。

1 应急物资分配−运输优化模型

1.1 问题描述

当地震灾害发生后，应急物资调配工作需要立即启动，灾区抗震救灾指挥机构会在灾区外围组建救援物资接收点，统一接收从全国各地捐赠的救援物资，各类应急物资均由集散点通过车辆运输或人力搬运方式向若干受灾点分配。地震灾害具有破坏性强、影响范围广等特点，因而灾区的各类信息获取难度增加，只能大致确定一个区间范围。震后救援物资需求量巨大，使得救援中经常出现应急物资不足的情况，且随着救援过程持续推进，物资需求信息和运输道路等各类信息可能会发生变化，初期对应的分配方案不适用于后一时段的实际情况。

因此，本文要解决的问题是：在不确定环境下各受灾点物资需求数量、灾区运输网络的通行能力动态变化的情况下，考虑物资供给数量有限、车辆的负荷装载能力、运输道路最大可分配车辆数等一系列客观约束，构建兼顾公平、时效和经济的多时段应急物资分配−运输规划模型，在确保应急物资按需分配和应急救援时效性的基础之上，降低物资运输成本。

1.2 模型建立

参数和决策变量表示如下。

根据问题描述，以各个受灾点需求满足率之差最小作为公平性指标，以配送时间最短作为时效性指标，以车辆运输成本最少作为经济性指标，建立的模糊机会约束规划模型如下：

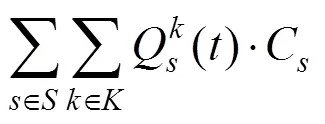
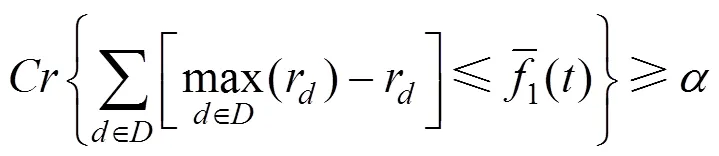
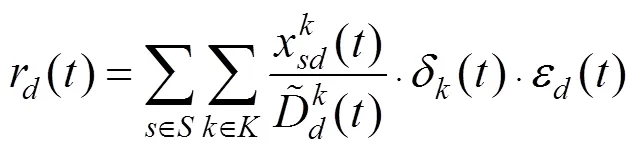
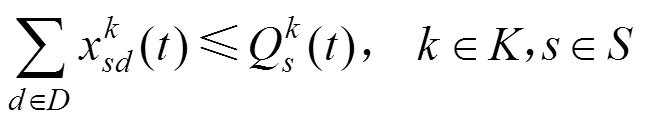
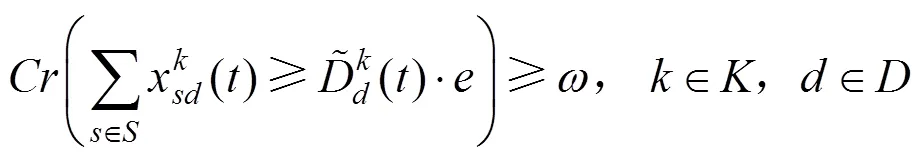
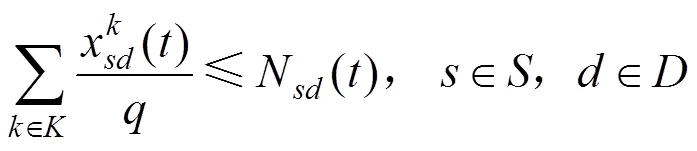
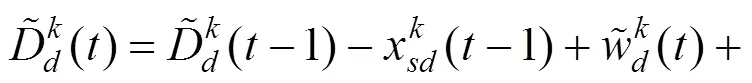
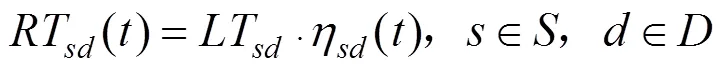
2 算法设计

针对本文构建的应急物资分配−运输多目标规划模型，首先基于滚动时域策略对动态决策问题进行处理，将动态应急物资分配−运输问题转化为一系列不同决策时刻的静态应急物资分配−运输问题。再采用转化法处理模糊机会约束条件得到清晰等价形式。最后针对多目标优化问题，由于每个目标相互制约、相互关联，决策者应根据灾区实际情况，综合考虑公平、时效、经济做出决策，因此，设计带精英策略的非支配排序遗传算法求解，它是基于遗传算法的多目标优化算法，利用其全局最优逼近思想，得到多目标Pareto最优解集，为决策者提供不同偏好选择。

2.1 不确定信息的处理

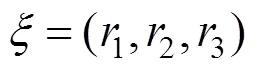
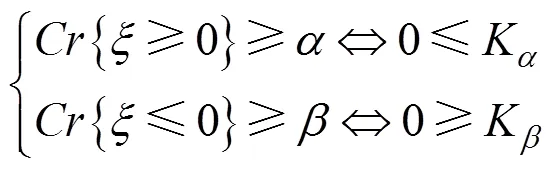
2.2 带精英策略的非支配排序遗传算法

1) 染色体编码。用二维矩阵实数编码方式描述每个时段集散点到受灾点的分配量和指派关系，然后进行取整，一条染色体代表一种应急物资分配方案，其中每一行代表一个集散点，每一列代表一个受灾点，每个基因表示物资集散点对受灾点的物资分配情况。

2) 生成初始群体。对于物资分配量和指派关系的初始种群，在满足约束条件的基础上随机均匀产生各基因位上的值。

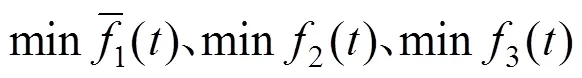
4) 非支配排序。对每个个体设有2个参数n，S，n表示在种群中支配个体的个体数量，S表示被个体所支配的个体集合。

①找出种群中所有n=0的个体，并将其存入当前集合1中；

②对当前集合1中的每个个体，遍历其所支配的个体集合S，对S中每个个体执行n=n−1，如果n−1=0，则将个体存入另一个集合；

③将1作为第一级非支配个体集合，赋予该集合内的个体非支配序rank()=1，继续对集合作上述分级操作，并赋予相应的非支配序，直到所有的个体都被分级。

5) 拥挤度比较。

①对每个个体，令拥挤距离i=0，=1,2,…,；

②根据个目标的目标函数值f的大小，对种群进行排序；

③第一个和最后一个个体的拥挤距离设为无穷大，即1=d=∞；

通过非支配排序和拥挤度计算后每条染色体都有2个属性：非支配序rank()和拥挤度d。因此可以得到拥挤度比较算子：对任意2条染色体和，如果rank()＜rank()或rank()=rank()且d＞d，那么染色体占优。

6) 遗传算子。将父代种群和子代种群合并到一起进行非支配排序，即保留父代优良个体直接进入子代，以防止Pareto前沿的解丢失。采用锦标赛选择方法对个体进行选择操作。染色体交叉和变异操作分别采用模拟二进制交叉方法和多项式变异方法，以维护种群的多样性。

3 算例分析

3.1 算例描述

假设地震发生后，已知条件如下：在灾区外围设有2个物资集散点(编号为1和2)，受灾地区有5个受灾点(编号为3～7)。取==0.9，单位时间运输成本为200元/h，单位物资存储成本为40元/t，车辆最大载重量15 t，最低需求满足率为0.75，各受灾点需要2类物资分别是生活用品和食物用品。第1和2时段物资的需求量(已根据转化法转换为确定数值)、集散点供应量、运输时间、运输时间延迟系数、最大可分配车辆数等相关信息如表1～5 所示。

另外，程序采用Matlab R2018a编程，相关参数设置如下：种群规模=200，最大迭代次数max=1 000，交叉概率p=0.5，变异概率p=0.05。

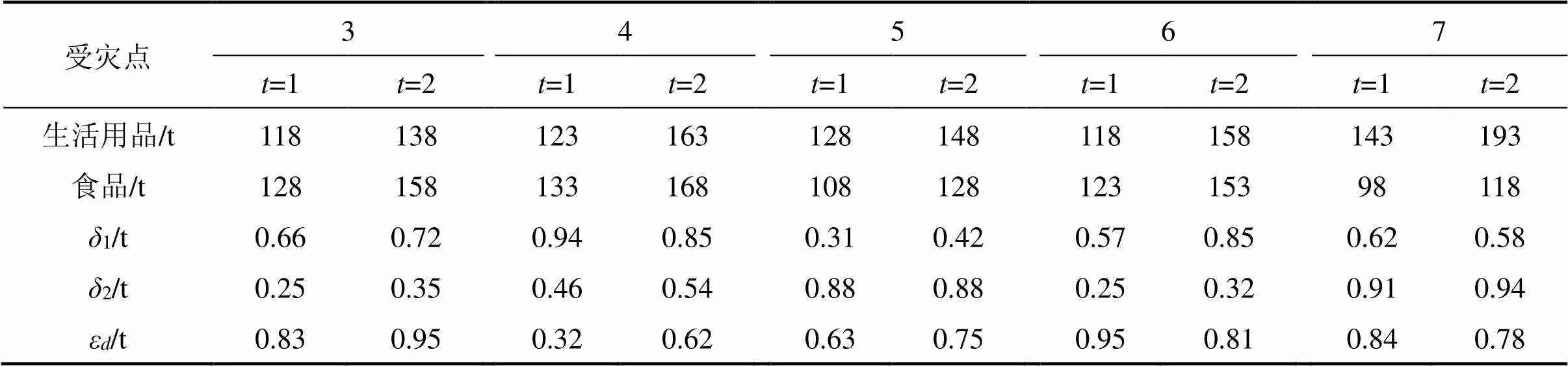
表1 受灾点需求量与各类参数

3.2 结果分析

通过运行程序，在迭代1 000次终止时，其迭代过程图如图1所示。随着迭代次数增加，染色体的适应度值最终收敛，取得了良好的收敛效果。程序运行耗时17.5 s，说明本文所建模型和算法的有效性。

表2 集散点供应量

程序运行结束后，所有解收敛到Pareto前沿面上，共求出200个可行解，=1时段Pareto最优解集分布如图2所示，从中抽取3组典型Pareto最优解如表6所示。

表3 正常情况下集散点与受灾点之间的运输时间

表4 受灾点与集散点之间的运输时间延迟系数

表5 受灾点与集散点之间道路最大可分配车辆数

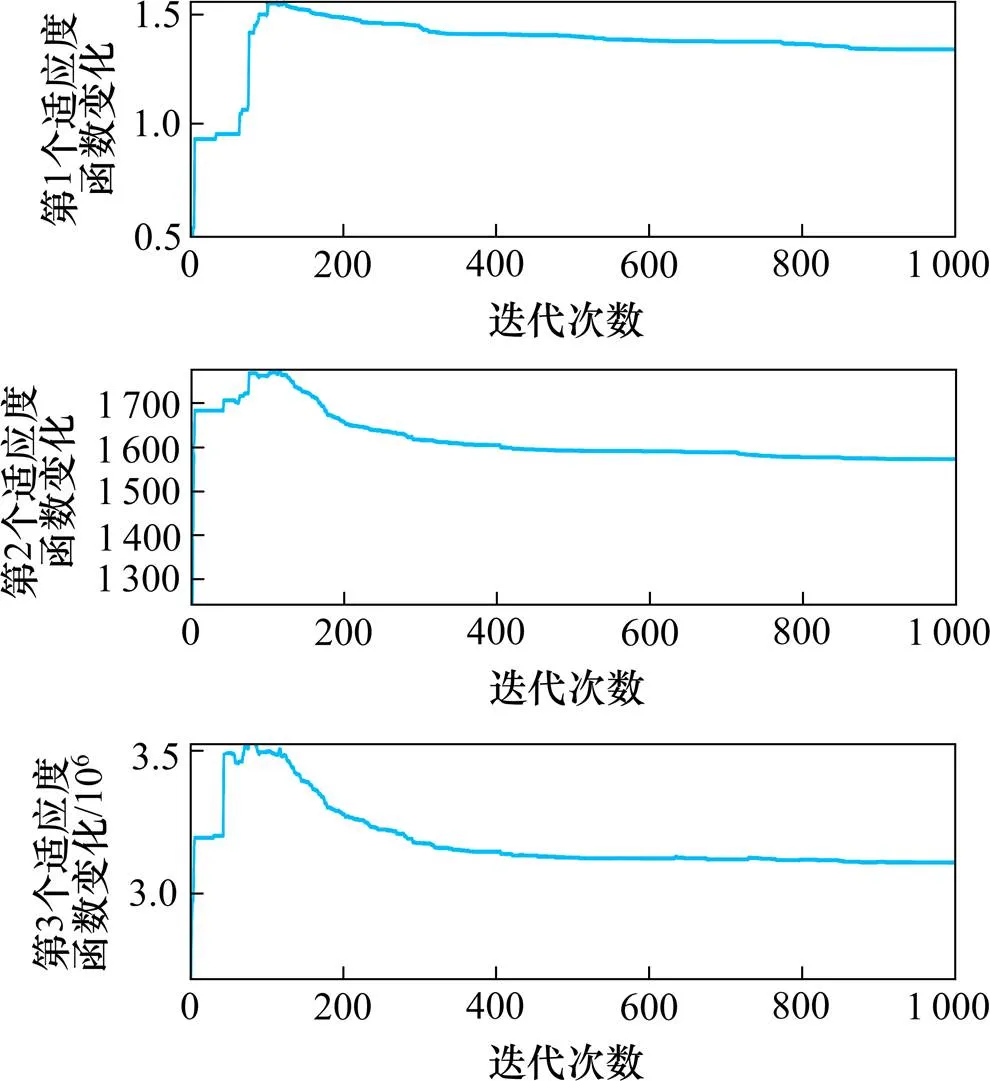
图1 t=1时段算法迭代过程图

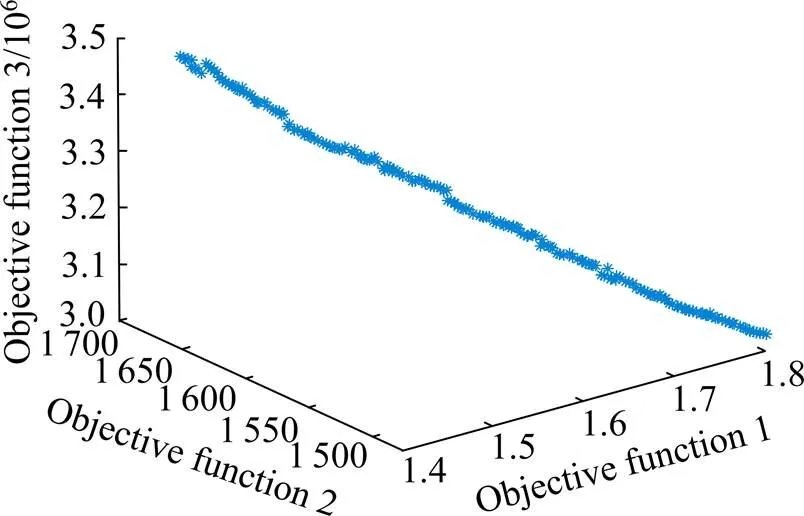
图2 t=1时段Pareto最优解集分布

第1时段物资分配−运输完毕后，灾区相关信息会发生变化，需重新制定下一时段分配−运输方案。同样通过运行本文设计程序，在迭代1 000次终止时，其迭代过程图如图3所示。随着迭代次数增加，染色体的适应度值最终收敛，取得了良好的收敛效果。程序运行耗时18.6 s，说明本文所建模型和算法的有效性。

表6 t=1时段典型Pareto最优解

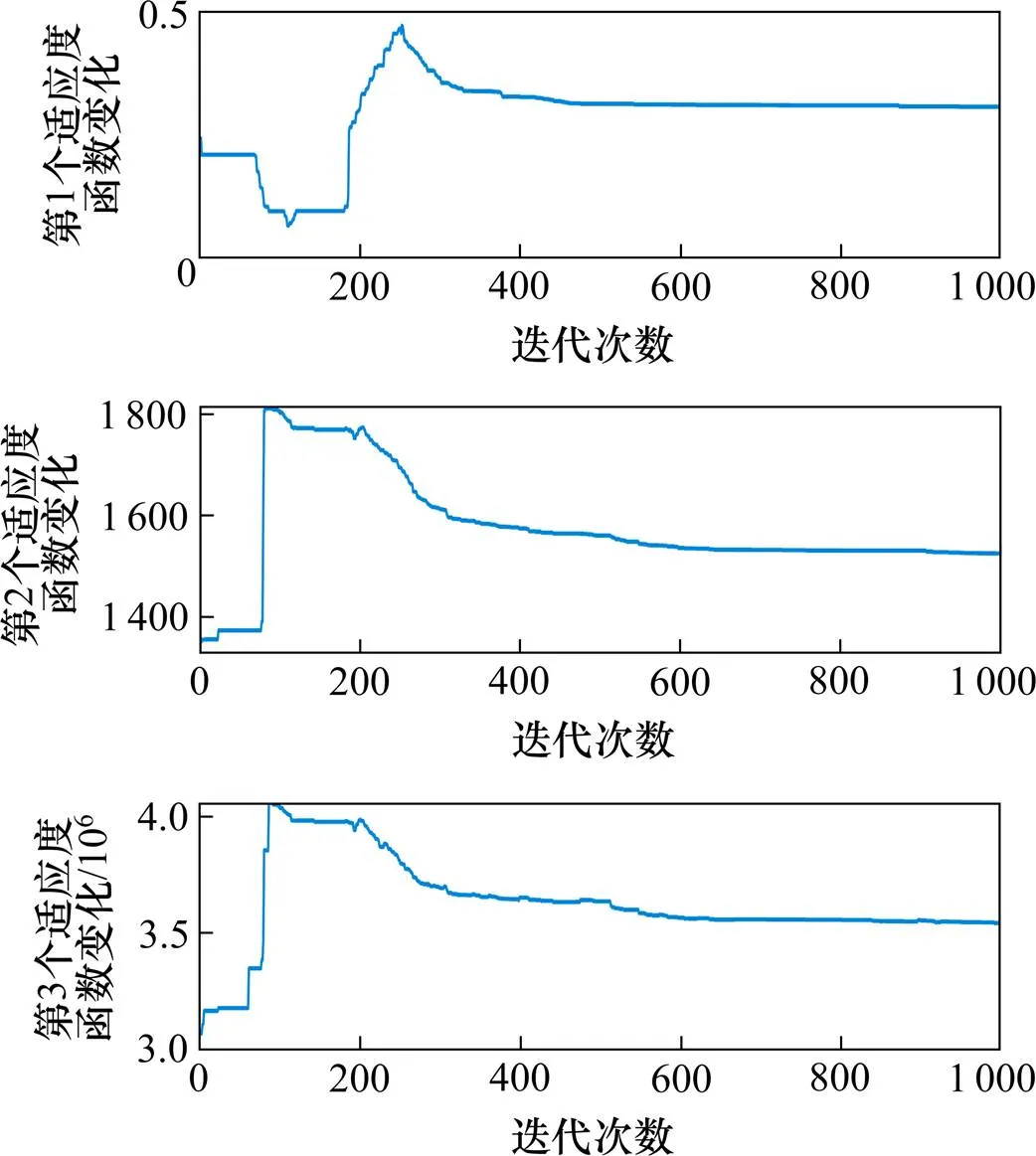
图3 t=2时段算法迭代过程图

程序运行结束后，所有解收敛到Pareto前沿面上，共求出200个可行解，=2时段Pareto最优解集分布如图4所示，从中抽取3组典型Pareto最优解如表7所示。

Pareto解A的分配−运输方案使各受灾点需求满足率基本维持同一水平，体现了应急物资数量分配的公平性原则。Pareto解B的分配−运输方案兼顾各受灾点需求满足率的公平性和物资到达时间的时效性。Pareto解C的分配−运输方案使各受灾点收到应急物资的时间最短、物资运输成本最低，体现了应急物资数量分配的时效、经济性原则。

图4 t=2时段Pareto最优解集分布

表7 t=2时段典型Pareto最优解

虽然有些受灾点物资需求量相同，但是物资分配量却不同，说明震后应急物资分配应综合考虑物资在该时段的效用与受灾点的需求紧急度等因素，不能单纯按比例分配或平均分配。

决策者可根据当期灾区的实际情况选择合适的物资分配−运输方案，在满足公平性和时效性的基础上，降低物资运输的成本。

4 结论

1) 针对震后灾区信息获取的不完全性和应急物资需求的动态性特征，采用机会约束规划方法，建立不确定环境下动态应急物资分配−运输多目标规划模型。

2) 通过算例验证本文设计的算法可产生有效的Pareto最优解及Pareto前沿，模型的公平性、时效性和经济性目标得到了兼顾，实现了震后应急物资分配运和输的集成决策。

3) 本文构建的模型是基于集散点和受灾点之间两层运输网络，涉及的运输方式只有一种，但现实救援过程中的运输网络往往更为复杂，需要多种运输方式联合运输。因此，研究多层应急物资运输网络、多种运输方式的物资运输−分配问题是下一步的研究方向。

[1] 王妍妍, 孙佰清. 模糊信息下多种类应急物资多周期分配优化模型[J]. 中国管理科学, 2020, 28(3): 40−51. WANG Yanyan, SUN Baiqing. Multi-period optimization model of multi-type emergency materials allocation based on fuzzy information[J]. Chinese Journal of Management Science, 2020, 28(3): 40−51.

[2] 付江月, 陈刚. 公平与效率权衡的双目标应急物资分配模型[J]. 系统工程, 2018, 36(6): 149−153. FU Jiangyue, CHEN Gang. A bi-objective emergency resources allocation model considering the trade-off between fairness and efficiency[J]. Systems Engineering, 2018, 36(6): 149−153.

[3] 王旭坪, 张娜娜, 詹红鑫. 考虑灾民非理性攀比心理的应急物资分配研究[J]. 管理学报, 2016, 13(7): 1075− 1080.WANG Xuping, ZHANG Nana, ZHAN Hongxin. Emergency material allocation model considering the non-rational psychological comparison of the victims[J]. Chinese Journal of Management, 2016, 13(7): 1075− 1080.

[4] 刘长石, 罗亮, 周鲜成, 等. 震后初期应急物资分配−运输的协同决策:公平与效率兼顾[J]. 控制与决策, 2018, 33(11): 2057−2063. LIU Changshi, LUO Liang, ZHOU Xiancheng, et al. Collaborative decision-making of relief allocation- transportation in early post-earthquake: Considering both fairness and efficiency[J]. Control and Decision, 2018, 33(11): 2057−2063.

[5] 李孟良, 王喜富, 孙全欣, 等. 基于鲁棒优化的应急物资多式联运调配策略研究[J]. 铁道学报, 2017, 39(7): 1−9. LI Mengliang, WANG Xifu, SUN Quanxin, et al. Research on allocation strategies of multimodal transportation for emergency resources based on robust optimization[J]. Journal of the China Railway Society, 2017, 39(7): 1−9.

[6] 陈则辉, 刘诚, 吕品, 等. 不确定环境下应急物资配送问题研究[J]. 铁道科学与工程学报, 2014, 11(5): 82− 89. CHEN Zehui, LIU Cheng, LÜ Pin, et al. Research on dispatching problem of emergency materials under uncertain environment[J]. Journal of Railway Science and Engineering, 2014, 11(5): 82−89.

[7] 田志强, 宋琦, 潘金山, 等. 铁路突发事件应急救援设备调度优化研究[J]. 铁道科学与工程学报, 2015, 12(1): 171−176. TIAN Zhiqiang, SONG Qi, PAN Jinshan, et al. Optimization analysis of equipment dispatching under railway emergency event[J]. Journal of Railway Science and Engineering, 2015, 12(1): 171−176.

[8] WANG Y Y, Bier V M, SUN B Q. Measuring and achieving equity in multiperiod emergency material allocation[J]. Risk Analysis, 2019, 39(11): 2408−2426.

[9] ZHU J M, LIU S Y, Ghosh S. Model and algorithm of routes planning for emergency relief distribution in disaster management with disaster information update[J]. Journal of Combinatorial Optimization, 2019, 38(1): 208−223.

[10] Matl P, Hartl R F, Vidal T. Workload equity in vehicle routing problems a survey and analysis[J]. Transportation Science, 2018, 52(2): 239−260.

[11] GUO Y, YE Y Q, YANG Q Q, et al. A multi-objective INLP model of sustainable resource allocation for long- range maritime search and rescue[J]. Sustainability, 2019, 11(3): 1−25.

[12] Gutjahr W J, Fischer S. Equity and deprivation costs in humanitarian logistics[J]. European Journal of Operational Research, 2018, 270(1): 185−197.

[13] Cotes N, Cantillo V. Including deprivation costs in facility location models for humanitarian relief logistics [J]. Socio-Economic Planning Sciences, 2019, 6(1): 89− 100.

[14] CHEN Y X, Tadikamalla P R, SHANG J, et al. Supply allocation: Bi-level programming model and differential evolution algorithm for natural disaster relief[J]. Cluster Computing, 2020, 23(1): 203−217.

[15] 刘宝碇, 赵瑞清, 王纲. 不确定规划及应用[M]. 北京:清华大学出版社, 2003. LIU Baoding, ZHAO Ruiqing, WANG Gang. Uncertain programming with applications[M]. Beijing: Tsinghua University Press, 2003.

Research on allocation-transportation problem of emergency materials in post-earthquake

WANG Xiaochun, MU Haibo

(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to achieve rapid and fair distribution of emergency supplies after the earthquake, this paper considered the uncertain demand of each disaster area, the complicated traffic situation of the road networks, the urgency of the requirement for reliefs in different disaster areas, the limited number of allocated vehicles on the road, and the long rescue period. Then, it used chance-constrained programming method to establish multi-period emergency materials allocation-transportation programming model. This goal was to minimize the difference in the satisfaction rate between different disaster areas, the time of emergency materials to reach the disaster areas, the cost of vehicle transportation and inventory. The fast and elitist non-dominated sorting genetic algorithm (NSGA-Ⅱ) was designed. Finally, the model and algorithm were proven to be effective through numerical example. Research results show that an effective Pareto optimal solution can be obtained, so decision-makers can choose the appropriate material allocation-transportation scheme basing on the actual situations.

emergency supplies allocation-transportation optimization; dynamic decision; fuzzy chance- constrained model; non-dominated sorting genetic algorithm

10.19713/j.cnki.43−1423/u.T20200535

U116

A

1672 − 7029(2021)04 − 1043 − 07

2020−06−16

国家自然科学基金资助项目(61563029)

牟海波(1977−)，女，辽宁朝阳人，教授，博士，从事交通信息工程与控制研究；E−mail：mhbmmm@mail.lzjtu.cn

(编辑 阳丽霞)