基于改进的Spearman 秩相关系数的直觉模糊多属性决策

郭 敏，田佳星

（中北大学经济与管理学院，太原 030051）

由于客观世界的复杂性以及决策者对客观事物认知的不确定性等原因，Zadeh［1，2］首次引入包含隶属度的模糊集来对事物的性质进行描述。Atanassov［3］在模糊集的基础上引入包含隶属度和非隶属度的直觉模糊集来描述事物的模糊性与不确定性，是模糊集十分重要的一种扩展形式，在处理客观世界中具有模糊性与不确定性的问题时更加准确、客观、细致。

直觉模糊集已经被广泛应用于多属性决策领域，其中属性间关联度以及属性权重方面的研究是多属性决策问题的核心。Deng［4］将灰色关联分析法应用于多属性决策领域以计算属性关联度；杨红军等［5］结合直觉模糊集概念提出了一种新的灰色关联分析法求解属性间关联度；而计算属性权重的方法总体上可以划分为主观赋权法、客观赋权法以及主客观组合赋权法3 种。主观赋权法包括AHP 法［6］、G1 法［7］、G2 法［8］以及 Delphi 法［9］等，得到的权重具有较好的解释性，不足之处在于无法体现属性实际数据在权重确定过程中的作用，其中最常用的是层次分析法；客观赋权法包括熵权法［10］、主成分分析法［11］、DEA 法［12］以及基尼系数赋权法［13］等，与主观赋权法恰好相反，主要依靠属性的实际数据来确定属性的权重，但权重稳定性以及可解释性却较差，其中熵权法是权重确定过程中利用最普遍的一种方法。由于上述两种赋权法优劣势并存，所以两者组合的主客观组合赋权法被提出，以综合优势、削弱劣势从而达到权重优化的目的。依据组合的效果将其分为基于向量层面的线性加权法［14］与基于元素层面的乘法归一法［15］。但加权系数具有强主观性的线性加权法和具有弱解释性的乘法归一法都不能在主观赋权法与客观赋权法得到的权重之间形成一种最优组合。而博弈论中均衡思想使双方利益得到最大化，因此基于博弈论的组合赋权法［16］应运而生，通过寻找折衷组合主客观权重使其与主客观权重之间的偏差之和最小，达到优化权重的目的。

在现有研究的基础上，本研究改进了Spearman秩相关系数的计算，提出以灰色关联分析法得到的关联度以及通过博弈论组合赋权得到的最优权重作为秩比较序列与秩标准序列，将其带入Spearman 秩计算中得到相关系数，将结果进行优序排列用以解决直觉模糊多属性决策问题。最后以实例和对比证明提出方法的有效性。

1 基础知识

1.1 直觉模糊集

定义1：设一给定论域为X∈[ 0,1 ]，则此论域X上的一个直觉模糊集A为：

式中，μA(x)表示A的隶属度函数，νA(x)表示A的非隶属度函数，并且满足 0 ≤μA(x) +νA(x) ≤ 1，对A上所有的x∈X都成立。直觉模糊集A上的一个直觉模糊数可以被表示为由隶属度μA(x)和非隶属度νA(x)所组成的有序区间对的形式直觉模糊集A的犹豫度可以被表示为πA(x) = 1-μA(x) -νA(x)。

定义2：正向最优集x+，记为

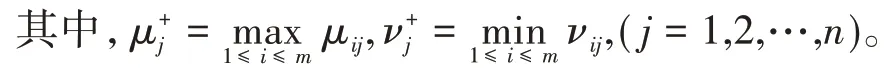
1.2 Spearman 秩相关系数

定义 3［17］：设自 变量X和Y的 2 个随机 样本为(x1,y1),…,(xn,yn)，将x1,…,xn和y1,…,yn按升序方式进行排列，则X和Y的Spearman 秩相关系数为：

式（1）中，表示为2 个秩的距离度量，di=R(xi)-R(yi),i= 1,…,n,R(xi)和R(yi)分别为xi和yi的秩。

2 主观与客观赋权法

设某一个多属性决策问题的方案集为A={A1,A2,…,An} ，每个方案对应的属性集为C={C1,C2,…,Cm} ，根据属性的特性可以将其分为效益型属性和成本型属性两类。

2.1 属性值的规范化处理

设aij为规范前的属性值，bij为规范化后的属性值。

根据直觉模糊集的性质，将规范化后的实值转换为直觉模糊数［18］，有μij=bij,νij= 1-bij，则属性值的直觉模糊数为

2.2 主观赋权法

层次分析法（AHP）不仅可以将多目标的决策问题分解为逐层渐进并相互影响的单目标问题，而且可以运用定量计算方法将定性指标具体化，令赋权结果更加符合实际要求。因此选择层次分析法来确定属性的主观权重。

1）构建直觉模糊判断矩阵。设有q位专家，各专家的评价权重为ξ=( )ξ(1),ξ(2),…,ξ(q)，q位专家依据表1 的指标评价等级确定各个指标层中指标的等级，并构建相应的直觉模糊判断矩阵(k= 1,2,…,q)，其中

表示第k位专家对元素i和j的重要性进行等级评价时，认为元素i优于元素j的程度；表示元素j优于元素i的程度。则集结q位专家对指标层指标等级评价的直觉模糊判断矩阵为：X=(xij)n×n=直觉模糊数指标评价等级标度见表1。

表1 直觉模糊数指标评价等级标度

2）一致性检验［19］。根据式（4）和式（5）计算直觉模糊判断矩阵的积型一致性判断矩阵当j＞i+ 1 时，有：

当j=i+ 1 时，则令当j＜i+ 1 时，则令

3）计算权重。将修正后并且符合要求的矩阵记为，为了便于运算，将中元素值转换为直觉模糊数：

2.3 客观赋权法

熵权法是一种通过信息之间差异性来进行赋权的算法，权重具有很强的解释性，并且可以与其他方法相结合使用，使计算出的权重更加客观有效。根据式（9）确定属性的客观权重。

式中，Ej是信息论中信息熵，若某个指标的信息熵Ej越小，代表其指标的变异程度越大，提供的信息量就越大，其权重也越大。

3 改进后的直觉模糊集Spearman 秩相关系数计算及多属性决策

Spearman 秩相关系数是统计学中计算变量之间相关性的重要指标，其在直觉模糊决策领域也有着十分广泛的应用。然而常见的利用Spearman 秩相关系数计算各方案间的相关性问题，仅将方案的各个属性秩大小进行编号后用于相关系数的计算，以最后所得值进行优序排列作为决策结果。此方法虽然计算简单，但却忽略了一个很重要的问题，尤其是对方案的属性值为直觉模糊数的决策问题而言，各方案的属性值之间是存在相互关系的，并且属性的权重在决策中也起到很关键的作用。上述这种不加限制的直觉模糊数的Spearman 秩相关系数计算是片面的，基于此，本研究提出一种改进后的直觉模糊集Spearman 秩相关系数，将各方案属性间关联度值序号作为秩对比序列，属性权重值序号作为秩标准序列，并在秩对比序列与秩标准序列之间建立一种Spearman 秩次相关关系，计算各方案Spearman 秩相关系数并进行优序排列，将其应用于多属性决策领域中。

3.1 属性间关联度的计算确定秩对比序列

1）属性间相关性对秩对比序列确定的影响。在一个属性值为直觉模糊数的多属性决策方案中，各方案属性间相互作用，某一方案的某个属性值的确定会受到其他各方案对应属性的影响，如何精确表示属性之间相互作用强弱关系，会直接影响最终的决策结果，而灰色关联分析的出现恰到好处地解决了这一问题。

2）灰色关联分析确定秩对比序列及比较分析。根据灰色分析法的思想，依据定义2得各属性下的正向最优集为x+，则各方案与x+的关联度εij记为［20］：

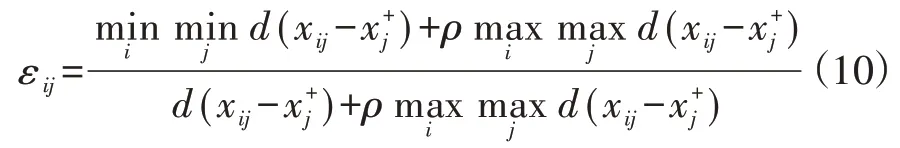
Spearman 秩相关性计算中，改进前的秩对比序列的确定仅通过属性值大小（直觉模糊数通过得分函数值比较）来进行排序，未充分考虑属性之间的关联性；改进后秩对比序列的确定通过灰色关联分析所得的属性关联度进行排序，充分考虑了属性之间相关性对排序的影响，使所得结果更有说服力。下面通过一个简单的例子对比改进前后秩对比序列的差异，设某个多属性决策的方案集以及对应的属性集为：

改进前方案A1秩对比序列为②③①；改进后方案A1秩对比序列为①③②。两者排序的差异必然影响最终的决策结果。

3.2 构建组合赋权法模型确定秩标准序列

1）属性权重未知对秩标准序列确定的影响。多属性决策方案中各属性的权重不仅代表各属性在总体中所占的百分比，更代表各属性的相对重要程度和贡献度，多属性决策方案中有些属性的权重可能很大，而有些属性的权重却可能很小，这会直接影响决策结果，而大多数Spearman 秩相关性计算中秩标准序列的确定都是在未充分考虑属性权重的前提下仅以各属性位置序号升序排列所得，忽略了属性权重所起的作用，从而弱化了各属性之间的差异性。如某个决策方案的4 个属性权重分别为（0.1，0.2，0.4，0.3），Spearman 秩相关性计算中秩标准序列，在未充分考虑属性权重前提下为①②③④；而在充分考虑属性权重的前提下却为①②④③，两者排序的差异会直接影响相关性分析的结果。

2）构建模型确定秩标准序列。设熵权法和层次分析法得到属性的权重向量分别为w1=(w11,w12,…,w1m)T、w2=(w21,w22,…,w2m)T，则两组向量的任意线性组合可以用矩阵的形式表示：

式中α1、α2为任意给定的线性组合系数，且满足α1≥ 0,α2≥ 0,α1+α2= 1。依据博弈论中均衡思想，通过寻求折衷主客观权重向量的最优组合系数求出两者之间的最优组合权重w*=进而得到以w*与w1、w2的离差总和极小化为最终目标的方法，对两组向量的线性组合进行优化，模型如下［16］：

利用混合罚函数对上述模型求解，使得原本有约束条件的模型通过将约束条件并入目标函数的方法转换为无约束模型，则上述模型可转换为如下模型：

3.3 改进后的直觉模糊集Spearman 秩相关系数计算

定义4：设各方案在各属性下的关联系数为εi,{εi=(εi1,εi2,…,εim);i= 1,2,…,n} ，各属性值的组合权重为则改进后的直觉模糊集Spearman 秩相关系数为：

3.4 多属性决策步骤

设某一个多属性决策问题的方案集为A={A1,A2,…,An}；各方案所对应的属性集C={C1,C2,…,Cm} ；属性权重未知；有q位决策者，决策权重为ξ=下面是在基于改进后的直觉模糊集Spearman 秩相关系数法的基础上，以方案间相关程度强弱为视角来解决多属性决策问题。具体步骤如下：①构建指标评价体系；②确定各方案间的各属性的灰色关联度，构建标准序列；③确定属性主观与客观权重间最优组合后的权重，构建对比序列；④运用改进方法计算各方案的相关系数，将所得的结果进行优序排列，以此决定各方案的优劣。

4 案例分析

以山西省高技术产业创新效率评价为例来验证改进后的直觉模糊集Spearman 秩相关系数决策方法的有效性与可行性。收集了山西省2009—2016年高技术产业方面的相关数据，将收集到的数据划分为准则层（4 个指标）和指标层（20 个指标），其中准则层4 个指标分别为高技术产业创新投入能力、高技术产业创新能力、高技术产业产业化能力和高技术产业创新环境能力，对山西省高技术产业创新能力进行评价。

4.1 数据来源

数据来源于2009—2016 年《山西省统计年鉴》《中国高技术产业统计年鉴》《中国火炬统计年鉴》《中国工业统计年鉴》以及山西省统计局网站。

4.2 山西省高技术产业创新能力评价及决策步骤

4.2.1 构建山西省高技术产业创新能力指标评价体系 从创新效率的角度将所收集到的高技术产业方面的数据划分为准则层（4 个指标）和指标层（20 个指标），构建山西省高技术产业创新能力指标评价体系（表2）。

4.2.2 确定主观权重 邀请3 位专家依据表1 对指标评价体系中的指标评价等级构建了18 个直觉模糊判断矩阵，其中3 位专家的评价权重分别为（0.5，0.3，0.2），将3 位专家对指标层指标等级评价构建的直觉模糊判断矩阵与各自所对应的评价权重进行结合，运用式（4）、式（5）将其转换为积型一致性判断矩阵，运用式（6）进行一致性检验，结果见表3。在满足一致性检验后计算准则层及指标层所对应指标的权重，然后将准则层各指标权重与其对应的指标层各指标权重相乘得到各指标的主观权重，结果见表4。由于篇幅限制，下文只给出专家对准则层中第一个指标所对应的指标层中各指标重要性相互比较所得的直觉模糊判断矩阵以及集结符合一致性的直觉模糊判断矩阵。

表2 山西省高技术产业创新能力指标评价体系

表3 一致性检验结果

根据以上计算得准则层的权重值为wA=[0.298 98,0.215 90,0.252 72,0.232 40 ]；指标层相对于准则的权重值为：

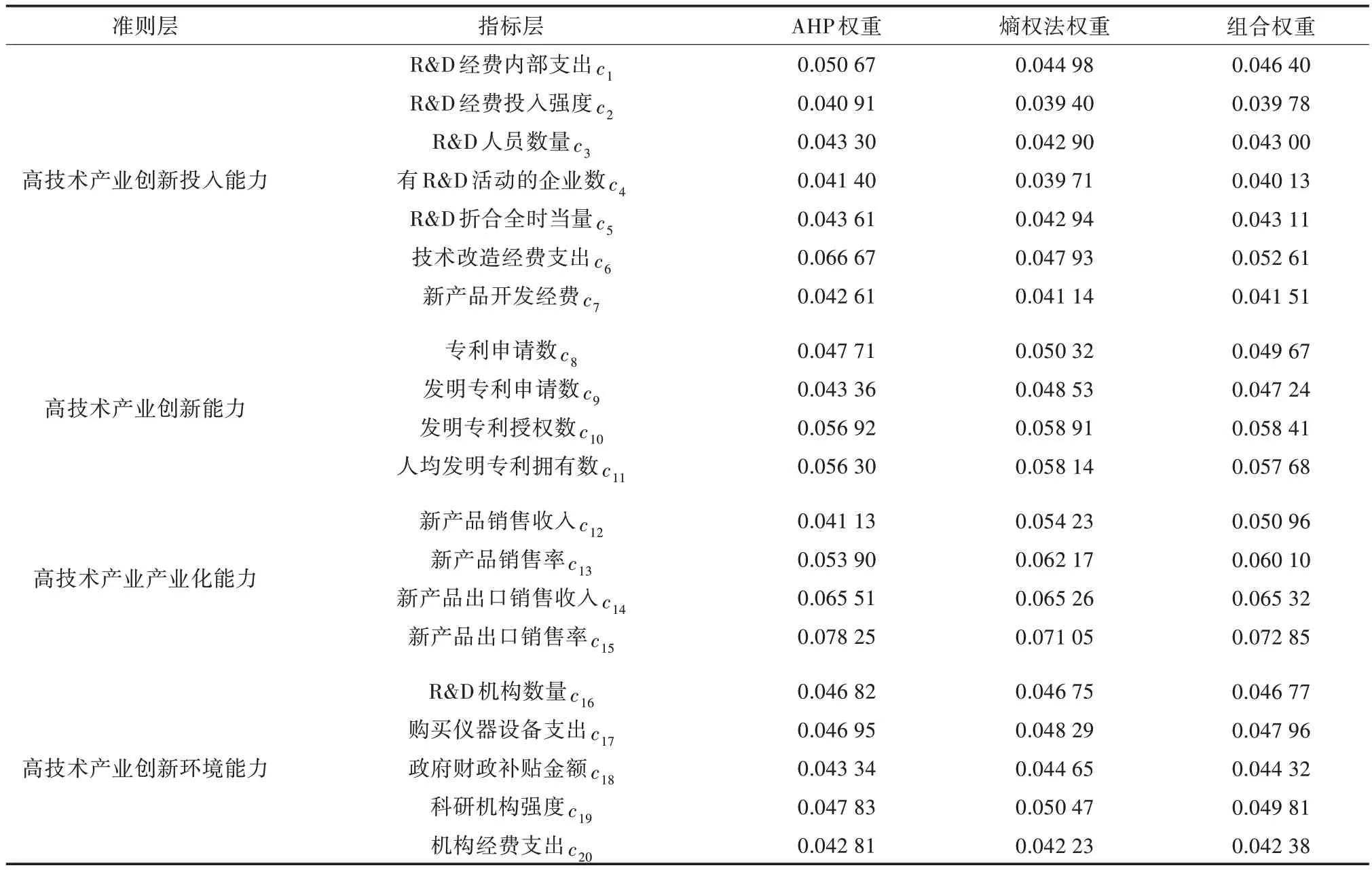
表4 主观权重、客观权重以及组合权重

4.2.3 确定客观权重 依据指标评价体系，运用式（2）、式（3）将收集到的数据进行规范化，并根据文献［18］将规范化后的数据进行直觉模糊化处理，结果见表5。运用式（9）计算各指标的客观权重，结果见表4。

4.2.4 确定组合权重 依据博弈论均衡思想构建优化模型，利用混合罚函数对模型进行求解得到最优线性组合系数从而得到优化后的组合权重见表4。

4.2.5 计算关联度 运用式（10）计算山西省2009—2016 年高技术产业创新能力指标的灰色关联度εij。

表5 2009—2016 年山西省高技术产业创新能力指标属性值

4.2.6 改进后的直觉模糊集Spearman 秩相关系数的多属性决策 运用式（12）计算得到山西省2009—2016 年高技术产业创新能力的Spearman 秩相关系数的值，如下：

将上述所得的各方案结果升序排列并作为决策的结果，排序为：Y8＞Y3＞Y7＞Y6＞Y2＞Y1＞Y4＞Y5。

4.2.7 比较分析 根据文献［21］计算得到山西省2009—2016 年高技术产业创新能力的Spearman 秩相关系数的值，如下：

得到的决策结果为：Y8＞Y3＞Y7＞Y6＞Y2＞Y4＞Y1。而Y5= -0.031，明显看出与其他决策结果的相关性方向不同，为负相关，故无法进行比较。由改进的直觉模糊集Spearman 秩相关系数计算所得的结果与文献［21］方法所得的决策结果相比较仅有个别决策结果排序不同，同时不存在相关方向差异的问题。这是由于本研究所提出的改进方法不仅考虑了属性权重对标准序列确定的影响，而且考虑了属性间相关性在对比序列确定中所起的作用，并在两者间建立了一种新的秩次相关关系，用来解决方案各属性的差异以及属性间的相互作用对决策结果带来的影响。

5 结论

目前，针对属性值为直觉模糊数且属性权重未知的多属性决策问题是研究的热点。本研究引入统计学中的Spearman 秩相关系数概念，并在基于直觉模糊集Speaman 秩相关系数的基础上提出了改进的Spearman 秩相关系数。其原理是将灰色关联分析法得到的各方案属性间的关联度值序号作为对比序列，组合赋权法得到的方案属性权重值序号作为标准序列，并在两者之间建立一种秩次相关关系来计算方案的秩相关系数，并将其用在多属性决策问题上。此改进方法克服了方案决策时由于忽略各属性的差异以及属性间的相互作用而导致重要信息流失、误差大等问题，在某种意义上可以说是对直觉模糊多属性决策问题进行了一定的补充和完善。最后，通过案例分析可以看出，本研究所提出的改进算法计算思路明确，综合评价结果合理性高，具有较强的实用价值。