残余力向量矩阵变化率的损伤诊断法

李国庆， 罗 帅， 苏 睿， 王泽铭， 汪 城

(绍兴文理学院 土木工程学院， 浙江 绍兴 312000)

近年来，关于损伤检测的研究依然是热点。当结构发生损伤时结构物理参数会发生改变，进而会影响其结构模态参数，通过对受损结构进行模态分析便可了解损伤状况[1～4]。近年来，结构损伤诊断方法有很多种，其中残余力向量法是运用广泛的结构损伤识别法，通过计算受损结构的残余力向量来实现损伤识别，此类方法具有流程简单、概念清晰、检测效率高等优势[5～7]。在实际工程中实测结构振型不完备是影响损伤识别精度的主要因素，为了使实测自由度数与有限元分析自由度数相匹配，杨秋伟等[8,9]在考虑结构惯性量的前提下提出一种结构自由度缩聚法，之后研究比较了残余力向量在各级缩聚下的精度。缩聚法可以有效地解决模态参数不完备这一问题，但由此导致的误差会影响损伤识别精度，另外主、副自由度的选取很大程度上决定着损伤识别结果的可靠性。何伟等[10]提出了一种自由度缩聚情况下的残余力向量法，验证了受损单元在振型节点位置或附近时此方法的有效性，但在考虑随机噪音干扰下此方法依然失效。基于此，本文提出一种运用残余力向量矩阵变化率的损伤识别法，通过推导模型自由度缩聚后的残余力向量公式，并计算出受损结构相较于损伤前的前几阶残余应力向量变化率矩阵，然后取变化率矩阵每行元素最大值的绝对值作为改进的残余力向量。算例研究表明：即使在随机噪音影响下，该方法仍然可以高效精确地识别出损伤单元，损伤识别结果优于传统的残余力向量法，较好地解决了噪音干扰及自由度缩聚对损伤识别精度影响这一问题。

1 模型缩聚后的残余力向量

结构损伤对质量的影响忽略不计，则n个自由度的结构损伤后振动方程为[11]：

(Kd-λd jM)φd j=0

(1)

ΔK=Ku-Kd

(2)

式中：Ku，Kd分别为结构损伤前、后的刚度矩阵；ΔK为结构损伤前后刚度矩阵的改变量；M为质量矩阵；λd j，φd j分别为受损结构的第j阶特征值和振型。

将式(2)代入式(1)可得：

(Ku-λd jM)φd j=ΔKφd j

(3)

令

bj=(Ku-λd jM)φd j

(4)

式中：bj为j阶残余力向量。在实际工程中实测振型通常是不完备的，需要对结构模型的自由度进行缩聚[12～14]。结构的振动方程可表示为：

(5)

由文献[8]可知，实测振型向量与完整振型向量之间的关系表示为：

(6)

其中转换矩阵T为：

(7)

(8)

由于在环境激励作用下测得的振型通常未做质量归一化，因此需要对实测振型进行归一化处理。众所周知，实测振型和质量归一化振型之间相差一个比例系数αj，即

ψj=αjφj

(9)

(10)

式中：w1，w2分别为附加质量前和附加质量后的频率；ψ1为未附加质量结构振型；ΔM为附加质量大小。

因此根据式(8)便可得到在环境激励作用下自由度缩聚后受损结构在全自由度下的残余力向量表达式：

(11)

2 改进的残余力向量法

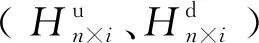
(12)

(13)

将式(12)(13)作差可得残余力向量矩阵差ΔHn×i：

(14)

将矩阵(14)的元素和矩阵(12)的元素对应相除可得到残余力向量矩阵变化率矩阵Ln×i：

(15)

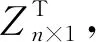
(16)

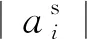
3 算例分析

以一简支梁算例来验证所提方法相较于传统残余力向量法的优越性。梁长6 m，截面积300×500 mm2，弹性模量E=3.2×1010Pa，密度ρ=2500 kg/m3，泊松比γ=0.3。简支梁划分25个单元，节点编号为1～26，每个节点有三个自由度：x，y及绕平面转动的自由度，模型如图1所示。分析可得，由简支梁节点绕平面转动的自由度计算出的残余力向量对损伤较为敏感，故本文将假设节点编号为6，11，16，21四个节点的转动自由度可以实测得到，其他节点的自由度均进行缩聚。通常结构损伤对质量影响非常小，故简支梁的损伤通过降低弹性模量来模拟[17]。为了使理论分析和实际环境相匹配，将模态分析得出的频率和振型引入噪音干扰[18]。

(17)

(18)

式中：w′i，φ′i为加入随机噪声处理后频率和振型；ε为频率引入的噪声水平；ζ，ξ为振型引入的噪声水平；rand(-1,1)为在-1～1之间均匀分布的随机数；rms(φi)为φi的均方根。

图1 简支梁模型

3.1 对实测振型进行质量归一化

使用附加质量法通过求解振型关于质量归一化比例系数来达到振型质量归一化目的，附加质量大小及位置按照文献[19]中使用附加质量法的原则，这里取附加质量大小为：ΔM=2Δm1+2Δm2=108 kg，具体附加质量大小及位置分布如图2所示。由式(9)可知质量归一化振型和实际工程中未质量归一化振型之间相差一个比例系数，通过式(10)求解出这个比例系数便可将实际工程中振型进行质量归一化。使用附加质量法将实际工程中振型进行质量归一化的结果和真实质量归一化振型之间的对比如图3所示，从图3中可以看出通过使用附加质量法求解出的前四阶质量归一化振型和真实质量归一化振型之间误差较小，说明附加质量法可以将实际工程中振型进行质量归一化处理且误差也较小。

3.2 单处损伤

简支梁第8号单元损伤10%记为损伤工况一，由模态分析计算出的频率和振型中加入随机噪音干扰[ε,(ζ，ξ)]=[15,(20,4)]。以前三阶的模态参数为基本量，接下来利用文献[20]中的方法进行损伤识别，识别结果如图4所示。从图中可以看出在随机噪音干扰下，文献[20]中的方法已经识别不出损伤单元，证明此方法在考虑随机噪音和模型自由度缩聚情况下是失效的。运用本文所提出改进的残余力向量法进行损伤诊断，其损伤识别结果如图5所示，从图中可以看出简支梁第8号单元所对应的节点编号8和9的残余力向量值发生明显突变，说明简支梁第8号单元是发生损伤单元。而且未损伤单元编号的残余力向量值非常小，不易引起误判，损伤识别结果非常精确和清晰，表现出本文所提出改进的残余力向量法具有较高的损伤定位性能和抗噪性能。

3.3 多处损伤

假设简支梁第8号单元和第18号单元分别损伤10%和20%，记为损伤工况二。对模态分析得出的频率和振型同样考虑随机噪音干扰[ε,(ζ，ξ)]=[15,(20,4)]。仍然以前三阶的模态参数为基本量，分别使用文献[20]中的方法和本文所提改进的残余力向量法进行损伤识别，将两者的识别诊断结果进行对比。文献[20]中方法的损伤识别结果如图6所示，从图中可以看出在随机噪音干扰下，对于两处损伤的情况该方法依旧识别不出损伤单元，未发生损伤单元的残余力向量值偏高，进一步说明该方法抗噪音干扰能力差。本文所提改进的残余力向量法进行损伤识别结果如图7所示，从图中可以看出简支梁第8号单元的节点编号8和9以及第18号单元的节点编号18和19的残余力向量值均发生明显突变，其他未发生损伤单元的残余力向量值较小接近于零，引起误判的可能性较小。此识别结果说明本文所提方法在模型自由度缩聚后依然具有较高的抗噪性。

图2 附加质量大小及位置

图3 振型对比

图4 文献[20]方法识别结果

图5 改进的残余力向量法识别结果

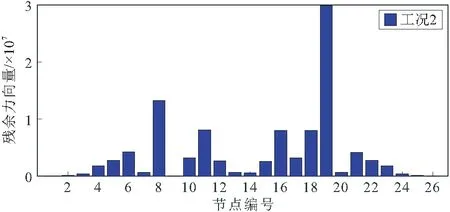
图6 文献[20]方法识别结果

图7 改进的残余力向量法识别结果

4 结 论

(1)本文研究了基于残余力向量法在模型自由度缩聚后的抗噪性，通过对结构损伤前、后残余力向量矩阵的运算，提出了残余力向量变化率矩阵这一概念。算例研究表明：本文所提的改进残余力向量法在模型自由度缩聚后具有较高的抗噪性，和传统的残余力向量法相比具有损伤定位明确、计算效率高、鲁棒性强等优点。

(2)在考虑随机噪音干扰下，运用现有的残余力向量法对模型缩聚后的结构进行损伤诊断，不管是单处损伤还是多处损伤其识别结果误差均较大，而本文方法的识别结果非常明确和清晰，凸显出了该方法具有较高抗噪音性这一优点。本文方法对实测自由度不完备这一问题提供了新思路。

(3)由于本文所提方法是基于简支梁绕平面转动方向自由度计算出的残余力向量为基本量，然而在实际工程中简支梁结构的转动自由度往往较难测量或者精度容易受到影响，因此本文所提方法还有待于完善和改进。