基于机器学习的交通流参数异常数据处理模型研究

周 博，贾树林，胡江宇，马双宝, ，罗维平,

（1. 武汉纺织大学 机械工程与自动化学院，湖北 武汉 430200；2. 湖北省数字装备重点实验室，湖北 武汉 430200）

随着私家车占有量急剧上升，城市交通网络所面临的负荷也与日俱增。在公路及城市道路中使用不同类型交通探测器收集实时交通数据，以对交通流进行预测、实时交通诱导以及道路通行能力预测分析提供及时可靠的数据支撑[1]。探测器收集数据的过程中存在诸多噪音，如设备的磨损导致精度的降低、雨雪天气对探头的影响及设备供电异常等，会对收集到的交通流数据质量产生一定的影响，因此需对收集的原始交通流数据进行故障数据的筛选修复。

针对交通流异常数据诊断，李琦等提出一种基于流量守恒定律的交通流数据质量评价与控制方法[2]，可对异常值进行整体修复，但该方法具有较强地域局限性，鲁棒性较低；苗旭等提出一种基于支持向量机模型的固定交通检测器缺失数据综合修复方法，可对交通流数据中缺失值进行填补[3]，但对于数据中存在的异常值未进一步处理；鲍东玉等人根据交通运行状态的统计相似性进行了研究和对比，选择了IQR法作为数据修复的方法[4]。综合前期学者研究，针对交通流数据的修复研究较为分化，缺乏较为完整数据处理体系，且大多基于统计原理，模型迁移能力有待提高。针对上述问题，本文提出基于机器学习及线性回归模型构建出一种综合数据清洗、奇异值、缺失值及异常值处理的交通流数据集成处理框架，对原始交通流数据进行有效性处理。

1 整体处理框架及数据来源

交通流数据主要包括速度、流量、时间占有率三个参数，数据采集过程中由于检测设备故障及检测环境对数据采集带来的影响，交通流数据中存在的问题数据可分为缺失数据、重复数据、错误数据三大类，根据问题数据类型对其进行有效性处理，其整体流程如图1 所示。本文所用数据来自兰州2018年一月份城市及高速交通检测器所采集原始数据集，采样间隔为五分钟，数据集来源于网络数据库。

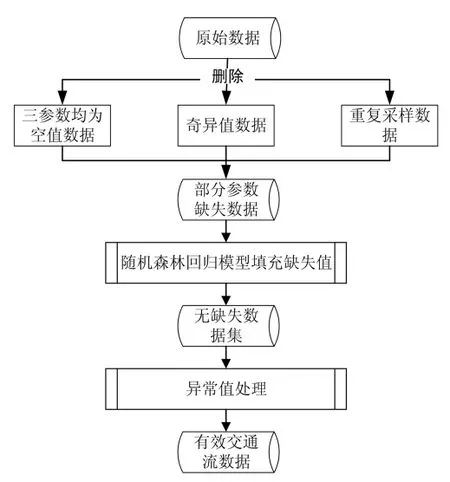
图1 数据有效性处理整体流程图

2 异常数据清洗方法

2.1 奇异值处理

首先对三参数均为空值的数据及重复采样的数据进行删除，再通过三参数的基本关系对数据中的奇异值进行删减。

对速度、流量、时间占有率三者关系进行相关性分析，当有车通过交通流数据采集器时三参数值均不为零；当无车通过采集器，三参数均为零；当车停在采集器边时，速度及车流量为零，占有率为100%；根据此交通流机理，可得到交通流数据奇异值基础筛选规则，如表1 所示（表中speed、occupancy、volume分别表示速度、时间占有率及流量）。

表1 交通流数据奇异值基础筛选规则表

根据表1 所提供的基础筛选规则可对原始数据中的奇异值进行初步筛选。

在交通流数据采集器的采样间隔内无车通过时，车辆服从泊松分布，其公式如式（1）所示。

其中p(x)为在采样间隔内通过采样间隔的车辆的概率密度函数，m为间隔内到达的平均车辆数，依据此在置信水平α下，交通流数据采集器采样间隔内有车辆到达的概率，即x＞0 的概率如式（2）所示。

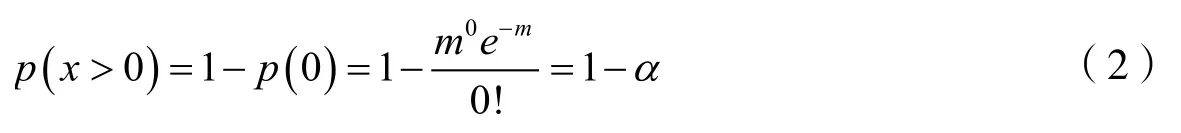
由此可得m=−ln α，可通过设置置信水平α进一步以概率来判断三参数均为零是否为异常值，即m ＞−ln α时，有1 −α的概率不会出现volume 为零的情况。

针对时间占有率为零其他两者不为零的数据，分析其原因可能是由于传感器不灵敏导致，根据交通流三参数线性关系如式（3）所示：

根据式（4）输入合理范围内的最大平均速度，平均有效车长及时间占有率即可得出最大流量阈值，并通过此筛选出奇异值。

2.2 基于随机森林回归模型缺失值处理

由于现有缺失数据插补方法主要包含单变量缺失值插补及多变量联立缺失值差补两大类，本数据集三参数均包含缺失值，为避免如均值填充、中值填充、上、下采样等单变量缺失值方法所造成的数据原始分布改变及产生抽样误差，本文采用多变量联立缺失值差补法对交通流数据集中缺失值进行填补。

通过对交通流三参数进行相关性分析，可以得到三参数相关性关系如表2 所示。

表2 速度、流量、时间占有率三参数相关性分析

由表2 中数据可知速度与时间占有率、流量与时间占有率之间具有较强的相关性，速度与流量之间具有中等相关性，因此，本文采用随机森林回归模型对速度、流量、时间占有率三个变量中缺失的数据进行缺失值填补。

随机森林是一种主流的机器学习算法，其底层是一种基于决策树的集成算法，由“Classification And Regression Tree（CART）”与“Bagging”方法结合而成，在建模过程中通过bootstrap 随机抽样的方法构建样本集以训练模型，模型输出结果是通过“投票”方式所决定的。由于其处理机制，随机森林对噪音数据及缺失数据具有较好的容错率，在处理高维数据时，能够自主进行特征选择，且抗过拟合的能力较强，鲁棒性较高[5]。

在交通流数据中，由于速度、时间占有率及流量三参数均存在缺失值，可根据变量缺失量由少到多的顺序对其缺失值进行填补。首先提取缺失数据最少的变量作为标签，对其余变量中的缺失值进行均值填充后，构建特征矩阵；其次对标签缺失值进行预测填补；最后使用填补完成的变量补充进数据集，再次进行排序及标签、特征矩阵构建，对三参数进行循环填补后即可得到完整无缺失交通流数据集。

3 异常数据处理

3.1 基于孤立森林的异常值提取

在得到的完整交通流数据集后，通过绘制核密度图观察数据分布情况，如图2 所示。

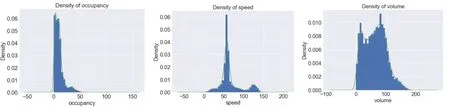
图2 完整数据occupancy、speed、volume 三参数核密度图

由图2 可知三参数中均具有离群值，需对其进行异常值处理。首先采用箱线法对数据进行异常值分析。对经过前期处理的交通流数据进行箱线法描述，其结果如图3 所示。

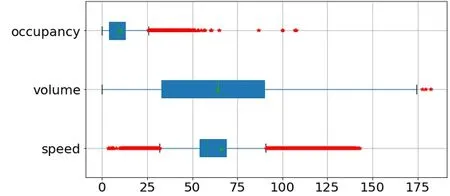
图3 交通流数据箱线法分析图

由图3 中数据可得，occupancy、speed、volume 三者均存在异常值。在speed 变量中存在较多偏大偏小数据，在volume 变量中存在少量偏大数据，在occupancy 中存在较多偏大数据。数据整体存在较多异常情况，因此需对数据进行进一步异常值处理。

本文采用Isolation Forest 算法对异常数据进行提取，由于Isolation Forest 模型是基于树模型的集成模型，因此在构建Isolation Forest 模型时首先需要通过数据训练出m多个iTree，其步骤如下：

（1）对于给定数据集X，采用随机抽样法抽取D个子集放入根节点：

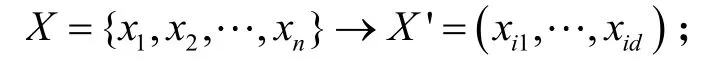
（2）从t个特征维度指定单个维度q，采用随机原则产生切割点p：

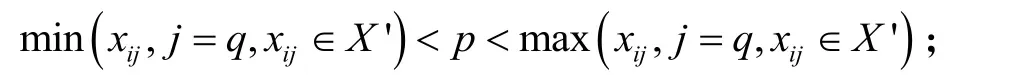
（3）对数据空间通过切割点p生成的超平面划分为两个子空间，对于维度小与p的放入左子节点，大于的放入右子节点；

（4）递归（1）、（2）至iTreed 达到预定高低；

（5）循环所有步骤，至m个iTree 生成。

孤立森林生成后，将单个样本输入iTree，计算其平均高度，并对其进行归一化处理，最后计算每个样本的异常值分数，分数计算公式如式（5）所示。

对于捕捉到的异常值，Isolation Forest 算法所提供的接口可将异常值所对应的数据索引进行缓存，便于对异常值处理后对应地填回数据。通过将交通流数据传入Isolation Forest 算法，得到的occupancy、speed、volume 三参数异常值数量如下表所示。

表3 速度、时间占有率及流量三参数异常值数量表

3.2 基于城市交通流参数的异常值填补模型

当交通流数据采集器采集到的数据中出现因硬件原因所造成的数据缺失的情况，可通过对交通流参数中两两之间构建关系模型，并通过已有数据对硬件故障进行数据修复，以进一步保证交通数据系统的正常运行。

3.2.1 速度-时间占有率模型求解

通过前期对交通流参数中速度与时间占有率两者关系进行分析得出两者具有很强的线性关系，因此建立一元线性回归的数学模型如式（7）所示：

式中s为交通流速度；m为时间占有率；c0、c1为回归系数及常数；ε为随机误差。此外，对于系统随机的误差需服从服从正态分布，满足如式（8）所示关系：

对于所构建函数模型中的参数，可通过最小二乘法计算得出。最小二乘法是通过最小化误差的平方和寻找参数的最佳匹配[5]。对于所构建的线性回归模型，需检验其可行性即准确率，其中包括回归方程及回归系数的显著性检验、残差分析等。对于有效的线性回归模型，残差应服从均值为0 的正态分布。对所得回归模型进行相关可行性检验所得计算结果如表4 所示。

表4 速度—时间占有率模型回归系数及显著性检验结果

由表4 数据可知，对于所求变量之间存在线性关系，且线性回归系数存在显著意义。最终得到利用最小二乘法得到速度-时间占有率的线性回归模型方程如式（9）所示。

3.2.2 流量-时间占有率模型求解

由流量-时间占有率散点图可以看出，数据点分布呈非线性关系，根据假设构建二元回归方程。建立流量-时间占有率二次曲线回归方程模型如式（10）所示：通

过线性变换m1=m2变换为二元线性模型为：

对构建的流量-时间占有率线性回归模型，输入数据进行拟合，使用最小二乘法参数进行拟合估计，求解出其回归模型，并对其进行相关性参数分析，其结果如表5 所示：

表5 流量—时间占有率模型回归系数及显著性检验结果

由表5 可知，经过计算，F 检验的概率p 值小于0.05 即流量与时间占有率之间存在二元线性关系;T检验的概率p 值小于0.05，即回归系数有显著意义[6-8]。最终经拟合检验得到的可行性流量-时间占有率模型如式(12)所示。

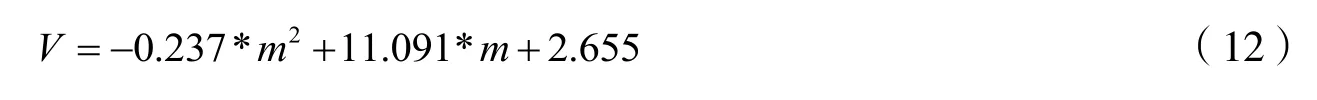
3.2.3 速度-流量模型求解

根据交通流三参数之间的相关性关系，对于速度-流量模型可联立前期求出的流量-时间占有率及速度-时间占有率模型对其进行求解，其中时间占有率作为中间变量。

通过联立式（9）及式（12）可得速度-流量模型如式（13）所示。

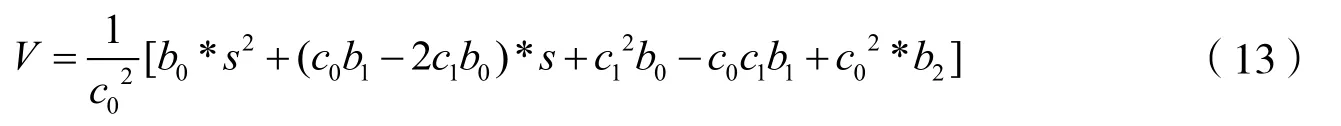
4 实验结果及结论

在得到三参数对应模型后将提取出的异常值及其相关参数输入模型，即可对异常数据进行预测，最终将所预测数据通过孤立森林模型中所保存的索引对数据进行替换，最终得到完整无缺失的数据集。

通过对数据集中异常值捕捉修正后，再次使用箱线法对数据整体进行观测，其结果如图4 所示。

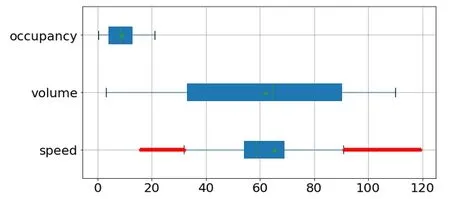
图4 修正后数据集箱线图

由图 4 中信息可知，经过处理后的交通流数据集volume、occupancy 两参数所有值均在正常阈值内，基本为正确数据，但speed 参数中仍存在大量偏离最大阈值范围的数，根据交通流三参数基本规律对speed、occupancy 两参数进行散点图描述如图5 所示。

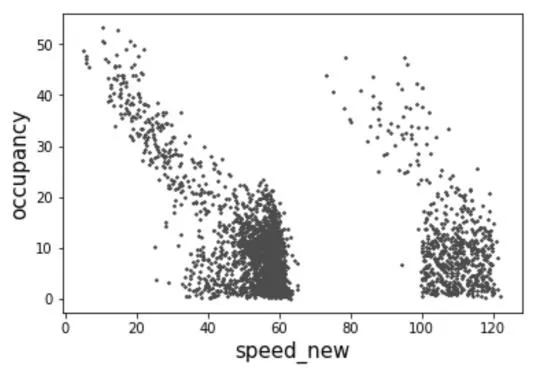
图5 车速-时间占有率关系图

由图5 信息可得，车速出现明显分段聚集，大致分为0～60km/h 及80～120km/h 两个区间，但在两个区间内数据基本服从交通流参数关系，即速度与时间占有率成反比关系。分析出现区间分化的原因是由于数据集中所采集的数据来源包括城市公路及快车道（高架、高速等），由于不同车道中速度限制及车道宽度的影响所造成的速度分化情况。在城市内道路中速度阈值大致为0～60km/h，在高架等快速车道速度阈值为80～120km/h，但在不同车道由散点图可知数据基本服从交通流参数关系，故通过箱线图表现出的速度异常值为正常数据。

对交通流数据的异常值进行判断修复是提高交通流信息数据有效性的基础，本文提出一种融合奇异值分析及孤立森林的交通流异常数据诊断方法，基于多元线性回归算法的异常值修复方法，经过实测数据检验，本文所构建数据处理模型可在很大程度上提升数据利用率，保证了交通流数据的可靠性与有效性，在今后研究中可对实时的交通流数据输出有效性方面进行改进。