超磁致伸缩作动器的磁路优化设计与有限元分析

涂建维，刘兆富，李 召

(武汉理工大学 土木工程与建筑学院，武汉 430070)

1 GMA的结构和工作原理

超磁致伸缩作动器结构如图1所示。主要包括输出杆、碟形弹簧、端盖、导磁侧壁、导磁环、导磁体、不导磁外壳和GMM棒等，其驱动部分由激励线圈和永磁体组成。超磁致伸缩作动器的工作原理为：以激励线圈产生的磁场作为驱动磁场，在结构上由上下导磁体、空气间隙、上下导磁环、导磁侧壁、永磁体与GMM棒形成闭合磁路[19]。当改变输入电流时，激励线圈会产生变化的磁场；由于GMM棒轴向的磁致伸缩效应，GMM棒会随着磁场的变化而发生伸缩变形，所以作动器会向外界输出位移和力，从而实现电磁能向机械能的转换。通过控制输入电流，可以控制作动器位移和力的输出。永磁体是为了提供偏置磁场而达到消除倍频现象的目的，同时使GMA具有较好的线性输出。蝶形弹簧提供一定的预压力，使GMM棒能够充分发挥材料的性能。

通过静态条件下GMM棒的线性压磁方程式(1)与式(2)[20]，可得出应变s和磁感应强度B之间的关系，如式(3)所示。

(1)

B=qσ+uσH，

(2)

(3)

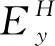
1—输出杆；2—碟形弹簧；3—上端盖；4—导磁侧壁；5—永磁体；6—激励线圈； 7—线圈骨架；8—下导磁环；9—下导磁体；10—外壳；11—GMM棒； 12—上导磁体；13—上导磁环；14—空气间隙图1 超磁致伸缩作动器结构简图Fig. 1 Structure diagram of giant magnetostrictive actuator

2 磁路设计

对于螺线管产生的磁场H与磁路总磁通φ之间的关系如式(4)表达所示[21]。

NI=φR，

(4)

图2 超磁致伸缩作动器磁路模型简图Fig. 2 Magnetic circuit model of giant magnetostrictive actuator

式中：N为螺线管线圈的匝数；I为线圈中的电流值；φ为磁通量；R为磁路中的总磁阻。

由图1可知，可以将作动器简化，得到磁路模型如图2所示。其中NI和F分别表示控制线圈和永磁体的磁动势；Rm、Rd、Rc、Rp、Rg和Ra分别表示GMM棒、上下导磁体、导磁侧壁、永磁体、上下导磁环和空气间隙的等效磁阻[22-23]。

其中：

(5)

(6)

式中：u0为真空磁导率；um、Am和Lm分别为GMM棒的相对磁导率、等效截面积和有效长度；ud、Ad和Ld分别为上下导磁体的相对磁导率、等效截面积和有效长度；uc、Ac和Lc分别为导磁侧壁的相对磁导率、等效截面积和有效长度；up、Ap和Lp分别为永磁体的相对磁导率、等效截面积和有效长度；ug、Ag和Lg分别为上下导磁环的相对磁导率、等效截面积和有效长度；r1、r2和h分别为上导磁体的外径、上导磁环的内径和空气间隙高度。由式(5)和式(6)可知，在GMA结构设计完成的情况下，要减小外磁路中的磁阻，需要增大导磁材料的磁导率；空气间隙Ra越小，外磁路中的磁阻越小，对GMM棒性能的发挥越有利。

由于超磁致伸缩材料和永磁体的磁导率都很低，因此，在实际的磁路中应考虑到漏磁。本文中所设计的磁路中同时包含激励线圈和永磁体2个磁动势，它们的漏磁强弱是不同的，分别用kf1、kf2定义激励线圈和永磁体的漏磁系数。由磁路欧姆定律可得：

(7)

由式(3)和式(7)，可得式(8)，

(8)

由式(8)可知，磁回路的结构形式、线圈的驱动方式和磁路中的导磁材料等均会对作动器的输出位移产生很大的影响。在作动器结构确定的前提下，对于高性能的GMA，需要对导磁材料的导磁率、上下导磁体的半径和激励线圈的轴向长度等进行优化。

3 磁致伸缩作动器磁场有限元分析

3.1 超磁致伸缩作动器有限元建模

电磁场理论主要是通过一套麦克斯韦方程组来描述的，它是用来分析和研究电磁场的[24-25]。如图1所示，由于GMA是三维轴对称结构，对其结构进行简化，采用平面轴对称单元(轴对称模型)建立有限元模型。利用ANSYS有限元软件对GMA磁回路进行有限元分析，具体的分析过程如下。

1)创建物理环境，选定Magnetic-Nodal，定义相关材料的材料特性，如表1所示；

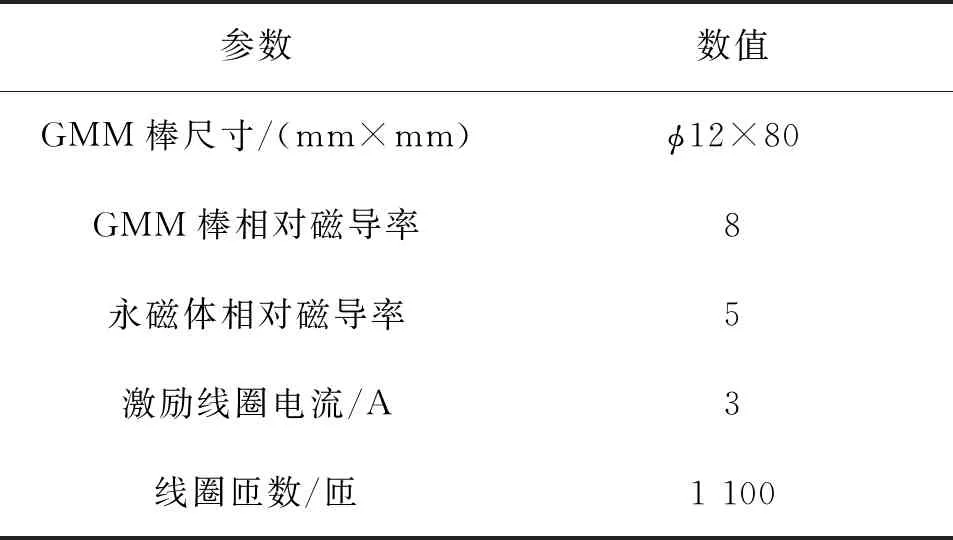
表1 模型材料的相关参数

2)采用面单元plane53建立模型、赋予材料属性、划分网格(图3)，这里采用的网格等级为4。对不同模型网格等级的研究表明，网格影响很小，考虑网格精度影响的结果见表2；

图3 超磁致伸缩作动器网格划分Fig. 3 Meshing of giant magnetostrictive actuator

表2 不同网格等级的磁感应强度与均匀度的对比

3)对所建模型施加磁力线平行边界条件，在线圈上施加电流密度面荷载；

4)通过MAGSOLV求解得到GMA内部磁感应强度分布以及GMM棒中的磁感应强度；

5)输出GMM棒磁感应强度计算结果。

以GMM棒中心线处的磁场均匀性作为磁回路优劣评价的标准，其值越接近1表示磁感应强度分布越均匀，表达式为

(9)

式中：Bmax为GMM棒中心线处的最大磁感应强度，Bmin为GMM棒中心线处的最小磁感应强度。

3.2 结构参数对GMM棒的磁场影响

3.2.1 开闭磁路对GMM棒的磁场影响

超磁致伸缩作动器内部磁路分别在开路和闭路的情况下，进行磁路分析。其中开路：上下导磁体、上下导磁环、导磁侧壁的相对导磁率均为1；闭路：上下导磁体、上下导磁环和导磁侧壁的相对导磁率均为100；无论开路还是闭路，GMM棒和永磁体的相对导磁率分别为8和5。通过有限元分析，得到开路和闭路时的磁感应强度分布分别如图4和图5所示。当磁路为开路时，GMM棒中的磁感应强度分布表现出中间大，两端小，磁感应强度分布极不均匀。当磁路闭合时，GMM棒中的磁感应强度的大小和均匀性均得到了很大的提高。将开路状态和闭路状态进行对比，其结果如图6所示。从图6中可以看出，GMA为闭路磁路时，磁感应强度远高于开路磁路的磁感应强度，且GMM棒中心线处的磁感应强度较为均匀。根据式(9)计算得到，开路时的均匀度为15.4%，闭路时均匀度高达85.9%，闭路时的均匀度相对开路时的均匀度提高了70.5%。因此，GMA内部的磁路应设计成闭合的。

图4 开路时磁感应强度分布图Fig. 4 Distribution of magnetic induction intensity in open circuit

图5 闭路时磁感应强度分布图Fig. 5 Distribution of magnetic induction intensity in closed circuit

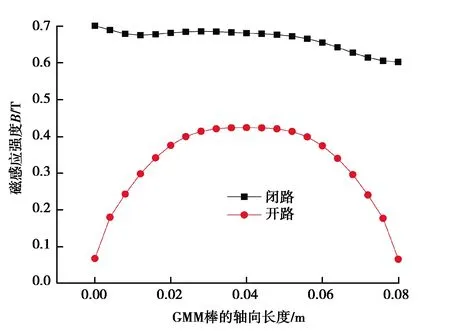
图6 GMM棒磁感应强度与开闭磁路的关系Fig. 6 Relationship between GMM rod magnetic induction intensity and opening and closing magnetic circuit

3.2.2 空气间隙对GMM棒的磁场影响

超磁致伸缩作动器在工作时，由于GMM棒的磁致伸缩效应，应该在输出杆与上端盖之间留有一定的空气间隙，便于GMA机械能的输出。而空气间隙的大小对于GMM棒中心线磁场分布影响非常大。空气间隙的大小直接决定漏磁的大小，所以当空气间隙大小分别为0.01，0.03，0.05，0.07，0.10，0.30 mm时，通过有限元分析，得到GMM棒中心线磁感应强度分布如图7所示，GMM棒磁感应强度的均匀度与空气间隙的关系如图8所示。

图7 GMM棒磁感应强度与空气间隙的关系Fig. 7 Relationship between magnetic induction intensity and air gap of GMM rod

图8 GMM棒均匀度与空气间隙的关系Fig. 8 Relationship between uniformity of GMM rod and air gap

从图7可以看出，GMM棒左端的磁感应强度较右端的大，且随着空气间隙的增大，GMM棒的磁感应强度逐渐减小。GMM棒左端的磁感应强度随着空气间隙的增大基本无变化，GMM棒右端的磁感应强度随着空气间隙的增大呈现大幅度的下降；这是由于空气间隙的增大，使GMM棒右端出现大量的漏磁现象，导致GMM棒右端的磁感应强度大幅减小。从图8可以看出，随着空气间隙的增大，GMM棒磁感应强度的均匀度逐渐下降，空气间隙为0.01 mm相对空气间隙为0.05 mm，GMM棒中磁感应强度的均匀度只提高了0.84%，空气间隙越小，意味着作动器结构设计成本越高。因此，在制作GMA时，应控制空气间隙小于0.05 mm，即能保证GMM棒中磁感应强度的均匀度高达95.49%。

超磁致伸缩作动器在工作时，应在输出杆与上端盖之间留有一定的空气间隙，便于超磁致伸缩作动器机械能的输出。设计时空气间隙最好小于0.05 mm，为了验证这个普适性，选用不同规格的GMM棒，通过改变模型的参数。分别取GMM棒的模型尺寸(mm×mm)为φ8×80、φ10×80、φ20×80、φ12×100和φ12×120来分别进行验证，其分析的结果分别如表3所示。

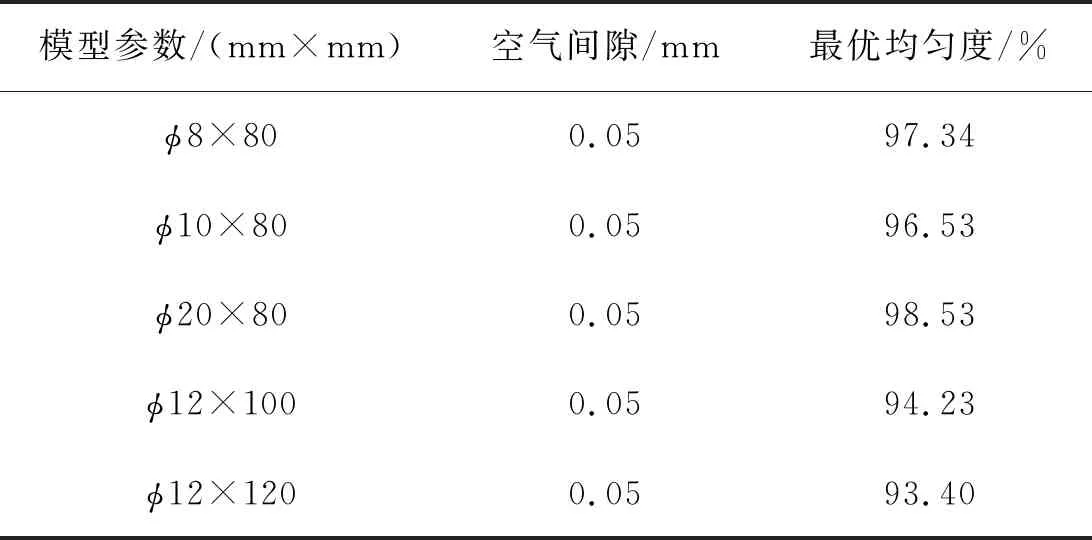
表3 模型参数空气间隙与最优均匀度

通过以上各种模型的仿真计算，其最终的结果表明，超磁致伸缩作动器设计空气间隙时最好小于0.05 mm，此时GMM棒中的均匀度最高。

3.2.3 上下导磁体的半径对GMM棒的磁场影响

根据磁路第一方程，穿出任意封闭面的磁通量恒等于穿入该封闭面的磁通量。为了改善GMM棒两端的漏磁，需要增加上下导磁体来减少端部的漏磁。由于GMM棒的导磁率仅为空气导磁率的3～10倍左右，因此GMM棒两端应设计高导磁的导磁体，导磁率高的导磁体可以使GMM棒中的磁感应强度更加均匀，导磁体的半径变化如图9所示。通过有限元分析，得到仿真结果如图10所示，GMM棒磁感应强度的均匀度与上下导磁体的半径的关系如图11所示。

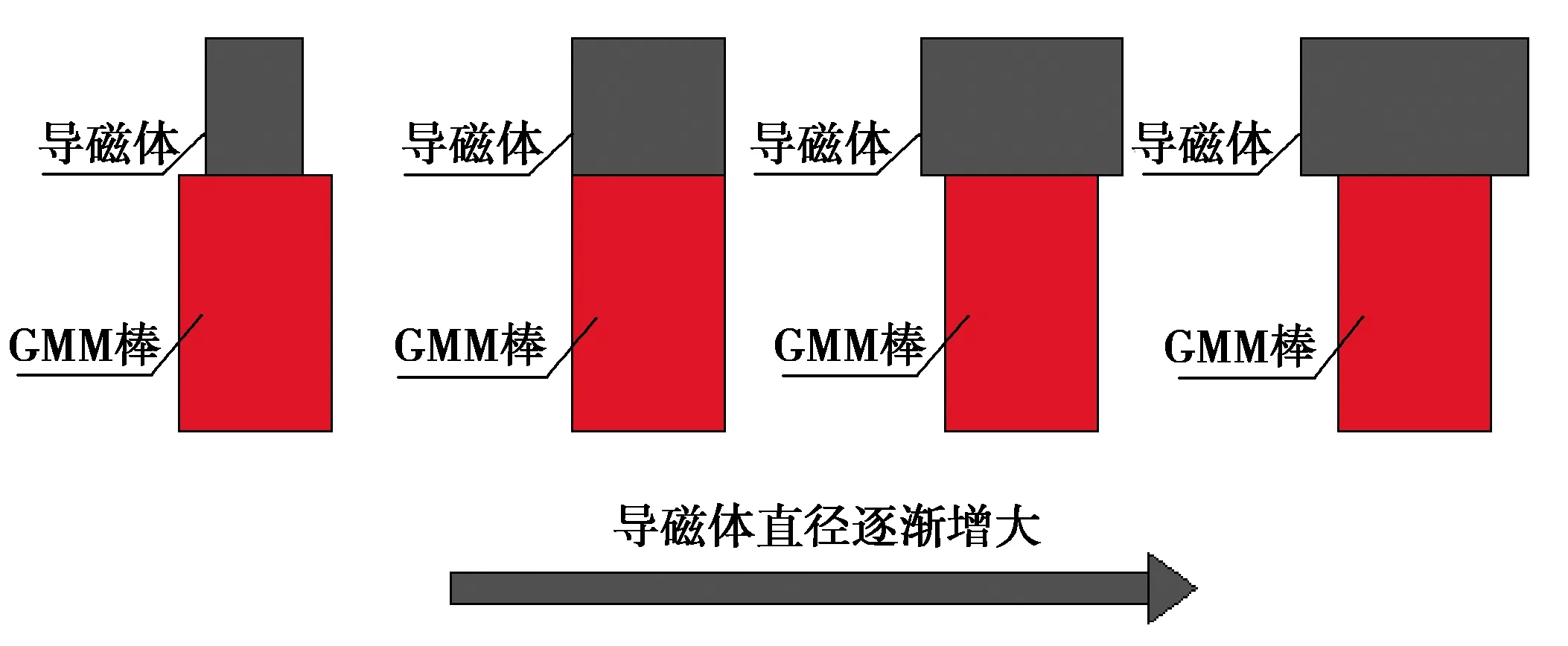
图9 导磁体半径的变化情况Fig. 9 Variation of radius of conducting magnet

图10 GMM棒磁感应强度与导磁体半径的关系Fig. 10 Relationship between the magnetic induction intensity of GMM rod and the radius of conducting magnet

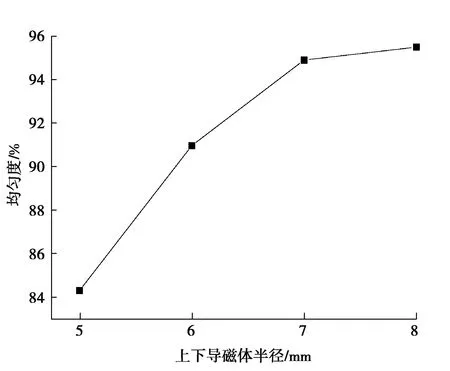
图11 GMM棒均匀度与上下导磁体半径的关系Fig. 11 Relationship between uniformity of GMM rod and radius of upper and lower magnets

根据图10可知，由于右端空气间隙的存在，增大了漏磁，使得每一种对应的导磁体半径左端的磁感应强度总比右端大。GMM棒磁感应强度的均匀度如图11所示，当导磁体的半径比GMM棒的半径小时，GMM棒中的磁场均匀度最差；当导磁体的半径与GMM棒的半径一致时，GMM棒中的磁感应强度较大，但均匀度相对较低；当导磁体的半径大于GMM棒的直径时，GMM棒中的磁感应强度相对较均匀，且导磁体半径为7 mm与导磁体半径为8 mm相比，GMM棒中的磁感应强度更大，均匀度相差很小。同时考虑到GMM棒易受到激励线圈工作时产生温度的影响，因此，在设计GMA时，导磁体的半径应略大于GMM棒的半径。

3.2.4 激励线圈轴向长度对GMM棒的磁场影响

考虑到空心螺线管端部磁场漏磁较大，因此应尽可能的将GMM棒位于激励线圈的中心位置，以改善GMM棒中心线磁场的均匀性。在保证其他结构参数不变的情况下，改变激励线圈轴向长度；通过有限元分析，得到仿真结果如图12所示，GMM棒磁感应强度的均匀度与激励线圈的轴向长度的关系如图13所示。

从图12可以看出，不同长度的激励线圈，所对应的磁感应强度是不一样的。通过式(9)计算，计算结果如图13所示。当激励线圈的轴向长度为84 mm时，GMM棒中心线的磁场均匀性最好，均匀度为96.43%；而当激励线圈的轴向长度为86 mm时，GMM棒中心线的磁场均匀性较低，均匀度为93.05%。并不是激励线圈的轴向长度越长，GMM棒中心线的磁场均匀性越好。因此在设计GMA中激励线圈的轴向长度最好为GMM棒长的1.05倍左右。

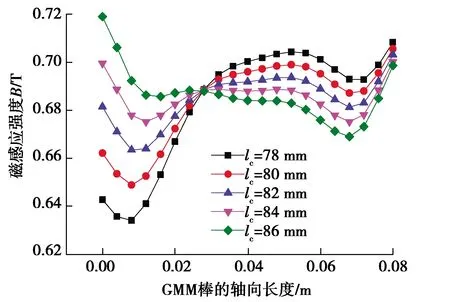
图12 GMM棒磁感应强度与激励线圈轴向长度的关系Fig. 12 Relationship between magnetic induction intensity of GMM rod and axial length of excitation coil

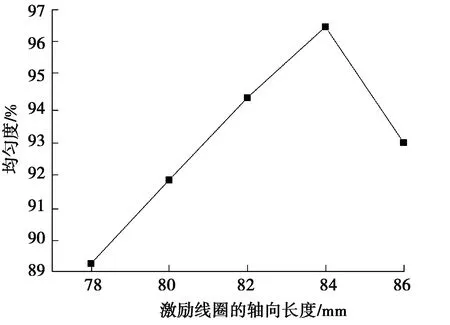
图13 GMM棒均匀度与激励线圈的轴向长度的关系Fig. 13 Relationship between uniformity of GMM rod and axial length of excitation coil

激励线圈轴向长度应设计为GMM棒轴向长度的1.05倍左右；为了验证这个普适性，选用不同规格的GMM棒，通过改变主要的模型参数。分别取GMM棒的模型尺寸(mm×mm)为φ8×80、φ10×80、φ20×80、φ12×100和φ12×120来分别进行验证，其分析的结果如表4所示。

表4 模型参数中比值与最优均匀度

通过以上各种模型的仿真计算，其最终的结果表明，激励线圈轴向长度应设计为GMM棒轴向长度的1.05倍左右，此时GMM棒中的均匀度最高。

3.2.5 磁路中导磁材料的导磁率对GMM棒的磁场影响

闭合磁路中，各导磁材料的相对导磁率的大小对GMM棒中磁场均匀性密切相关。当上下导磁体、上下导磁环和导磁侧壁相对导磁率分别为100，500，1 000，2 000，5 000时，通过有限元分析，得到材料的相对导磁率与GMM棒中磁场强度的关系如图14所示，GMM棒中磁感应强度的均匀度与导磁材料的导磁率的关系如图15所示。

从图14可以看出，当导磁材料的相对导磁率为100时，GMM棒两端的磁感应强度较小，中间磁感应强度大。造成的原因是，由于GMM棒两端的导磁体的相对导磁率低，导致GMM棒两端漏磁较为严重，从而影响GMM棒两端的磁感应强度。而当导磁材料的相对导磁率大于500时，随着导磁材料相对导磁率的增大，GMM棒的磁感应强度也随着增大，但是增大的幅度慢慢减小；GMM棒两端与中间的磁感应强度相差较小，GMM棒中心线磁场分布较为均匀，原因是GMM棒两端导磁体的相对导磁率较高，限制了漏磁。从图15可以看出，当导磁材料的导磁率大于500时，GMM棒磁感应强度的均匀度变化不大。因此，在设计GMA时，应选择较高的导磁材料，较高的导磁材料对于GMM棒中磁场分布的大小和均匀性都有利。

图14 GMM棒磁感应强度与导磁材料 相对导磁率关系Fig. 14 Relationship between magnetic induction intensity of GMM rod and relative permeability of magnetic conducting material

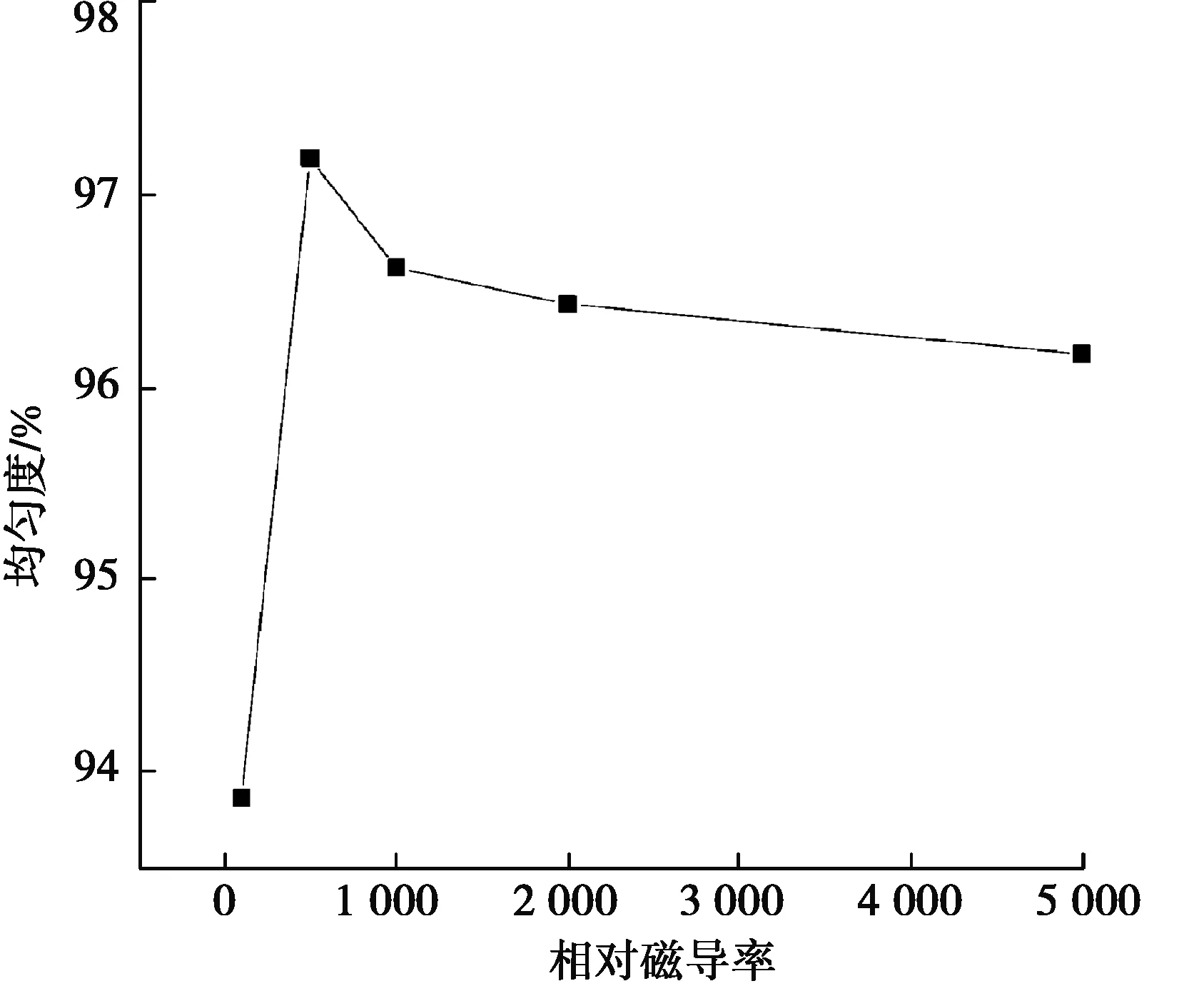
图15 GMM棒均匀度与相对导磁率的关系Fig. 15 Relationship between uniformity of GMM rod and relative permeability

3.3 作动器结构参数优化前后的对比

图16 优化后磁感应强度分布图Fig. 16 Distribution of magnetic induction intensity after optimization

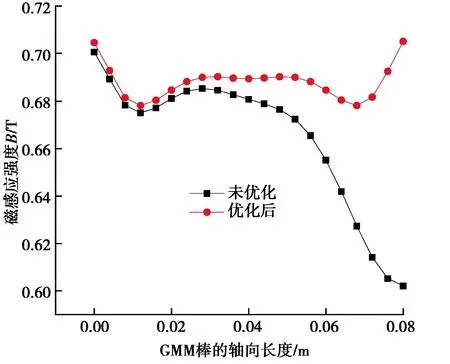
图17 GMM棒磁感应强度优化前后的对比Fig. 17 Comparison before and after optimization of GMM rod magnetic induction intensity

4 结 论

超磁致伸缩作动器内部磁路比较复杂，基于静态条件下线性磁致伸缩理论，并根据电磁学原理得出应变和磁路结构参数、材料相对导磁率的关系。在此基础上建立GMA的有限元模型，对其进行磁场仿真分析。通过GMA的磁场仿真结果研究，可以得出以下结论：

1)超磁致伸缩作动器内部的磁路应采用闭合的形式，无论是GMM棒中磁感应强度的大小还是均匀度都得到了大幅度的提高；同时磁回路应采用高导磁率的导磁材料，高磁导率的导磁体对GMM棒中磁感应强度的大小和均匀度都有利。

2)过长或过短的激励线圈轴向长度都会使GMM棒中磁感应强度的大小和均匀性受到影响，所以激励线圈轴向长度应设计为GMM棒轴向长度的1.05倍左右；为了增大GMM棒中磁感应强度的大小和均匀度，同时减小温度对GMM棒性能的影响，上下导磁体的半径应略大于GMM棒的半径。

3)输出杆与上端盖之间的空气间隙会使磁回路出现漏磁现象，过大的空气间隙将影响GMM棒磁感应强度的大小和均匀性。因此，设计时空气间隙最好小于0.05 mm。

4)通过作动器参数优化前后GMM棒中磁感应强度的对比，优化后，GMM棒中磁感应强度的大小提高了0.1 T，且均匀度提高了10.27%。