多股道站场牵引网故障定位方案研究
张 希,林国松,王 牣
0 引言
近年来,随着我国电气化铁路建设的不断推进,采用带回流线的直供方式已占铁路供电总比重的55%~65%。在电气化铁路网建设进程中,多股道站场接触网线路的交汇点和分岔点不断增加,且线路露天架设,运行环境恶劣,易发生故障[1]。站场股道发生短路故障将直接影响供电系统的稳定性,因此及时确定多股道站场故障点位置对保障线路的正常运行具有重要意义。
目前,常用的故障测距原理主要包括电抗测距、AT吸上电流比、上下行电流比等方法[2]。采用AT供电或复线直供方式的简单输电线路发生短路时,常用上述方法作为理论基础进行故障测距的研究。而对于采用带回流线的直供方式的站场,尤其是具有3条线路以上的复杂站场的故障定位,上述故障测距原理并不能完全适用,现有的故障定位方案仍存在一些问题,如测距误差较大,方案可行性小等。因此,对多股道站场的故障定位方案仍需进一步研究改进。
基于上述问题,本文对采用直供加回流的站场股道进行分组研究,通过电流大小定位故障股道,针对股道两端架设的电流信息采集装置,提出以电流比值为基础对故障线路进行故障测距的计算方法,并利用Matlab/Simulink搭建仿真模型对方案进行可行性研究。
1 直供牵引供电系统接触网
1.1 带回流线的直供方式
对于采用带回流线的直供方式的牵引供电系统,其线路主要由接触线T、回流线N、钢轨R组成[3],如图1所示。在带回流线的直供系统中,回流线并联架空在钢轨侧上方,组成一个回流系统,因此可以将回流线和钢轨作为“回流线+轨道”系统,计算时可等效为一条接地线路[4,5]。
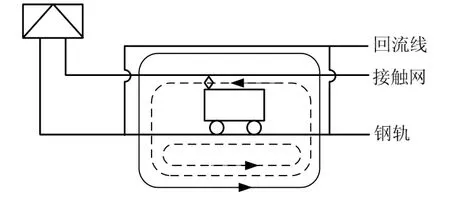
图1 带回流线的直接供电方式示意图
根据文献[3]关于复线牵引网阻抗的理论(Carson理论)可以得到对称布置且末端相连线路的等值阻抗Z3计算式:

式中:Z1、Z2分别表示两条线路各自的对地单位自阻抗,Z12表示两条线路对地的单位互阻抗;r1、r2分别表示线路1、2的电缆直径;n1、n2分别表示线路1、2的裂相数目;D1、D2、D12表示导线间的几何均距;Dg为等值深度,都与大地电阻率相关,一般取值930 m。通过Carson理论计算出“回流线+轨道”系统等值阻抗及与接触网相关的其他线路的阻抗参数。
1.2 接触网线路分组
站场内股道数目较多,且线路长度一般为1~2 km,距离相对较短,根据毕奥-萨伐尔定律,有

式中:B为磁感应强度,I为电流,μ0为真空磁导率,a表示平行导线的间距。一般而言,正常运行时流过直供牵引供电系统接触网线路的电流大约为500 A,2条线路中心间距约为6 345 mm,不同间距的平行导线相互之间的电磁干扰不同,如图2所示。

图2 导线间距对磁感应强度的影响
分析图2发现:相距2~3个线路中心间距的2条导线间的磁感应强度约为相距1个线路中心间距时的50%;当2条平行导线相距4个线路中心间距以上时,线路之间的电磁影响极小,可忽略不计。
高压输电线路电流较小,且相距较远的2根导线之间的互阻抗的数量级通常在0.01~0.1 Ω范围。在牵引网额定电压为25 kV的情况下,根据牵引网线路相关计算(式3)可知,相距较远的2根导线之间的互阻抗对线路电压、电流的影响几乎可以忽略不计。
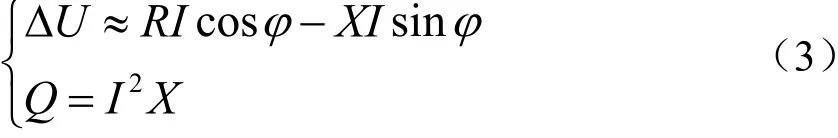
式中,ϕ表示电流的相位角,单位长线路阻抗为Z=R+Xi,Q表示线路传递的无功功率。根据式(3)可知,相距较远的2根导线之间的互阻抗对线路电压、电流的影响几乎可以忽略不计。
综上分析,可将站场接触网线路根据分岔点、交汇点和线路间距离的远近情况进行分组研究,从而提高电抗测距法的计算精度。
多股道站场上行、下行距离较远且末端未并联,可不考虑上、下行接触网-地回路的互阻抗对网压的影响,将接触网分成上行和下行两部分分别进行考虑。将上行(或下行)分岔线路中起点和终点相距50 m以内的2~3条线路视作1组,只考虑组内相邻线路-地回路的互阻抗,忽略不同组线路之间的互阻抗。
例如,某站场上行架设了5条接触网线路(图3),C、F两点之间横向距离约为50 m,可以看作为同一点。CD段和FD段相距较远,不需要考虑两条线路的互阻抗。最终可根据分岔位置不同将其分为Ⅰ、Ⅱ、Ⅲ 3组线路进行研究分析,若AB段距离小于200 m,可考虑不对Ⅲ组进行测距。
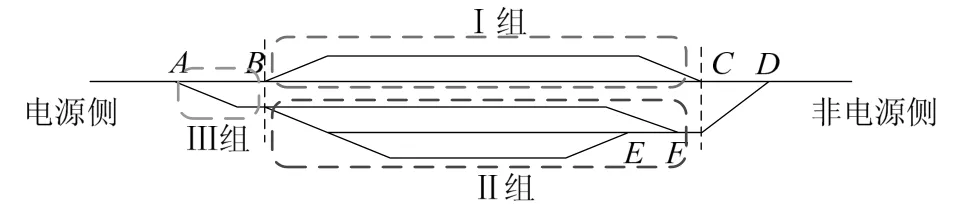
图3 多股道站场上行接触网分段、分组示意图
当输电线路发生短路故障时,可先判断出故障点所在股道,再利用股道上的电流信息计算出故障点的位置。
1.3 故障信息采集装置分布
由于站场内股道数目较多,对故障线路定位判断也更加复杂。当某线路发生短路故障时,该线路左右两端检测到的电流大小相差较大。可以通过在股道两端距上网点几米内的位置安装线路采集装置用于判断电流方向。当某一股道发生故障时,该线路左端电流将明显大于右端电流,通过比较电流大小得到故障点所在股道。
根据站场股道的分岔点和交汇点设置采集装置(图4),在分岔点后的每条线路和交汇之前的每条线路上分别安装采集装置。文献[1]提出了通过采集站场股道接触网承力索的电流电压数据,快速准确判定出故障股道的方案。根据该方法,对于股道距离通常在2 km左右的站场,线路单位长度自阻抗约为Z1= 0.145 + 0.400i,正常运行时线路两侧电流差几乎为0。故障点在线路中部时,线路两侧电流差ΔI1与线路其他点发生故障时的电流差ΔI2相比,ΔI1明显小于ΔI2,此时结合线路电流作为判断依据,降低误判的可能性。为避免外界因素造成电流故障误判,假设线路两端采集到的电流分别为I1、I2,当I1、I2均大于800 A且电流增量|ΔI|≥450 A时,或当I1或I2小于800 A且电流增量|ΔI|≤450 A时,认为该股道发生短路故障。
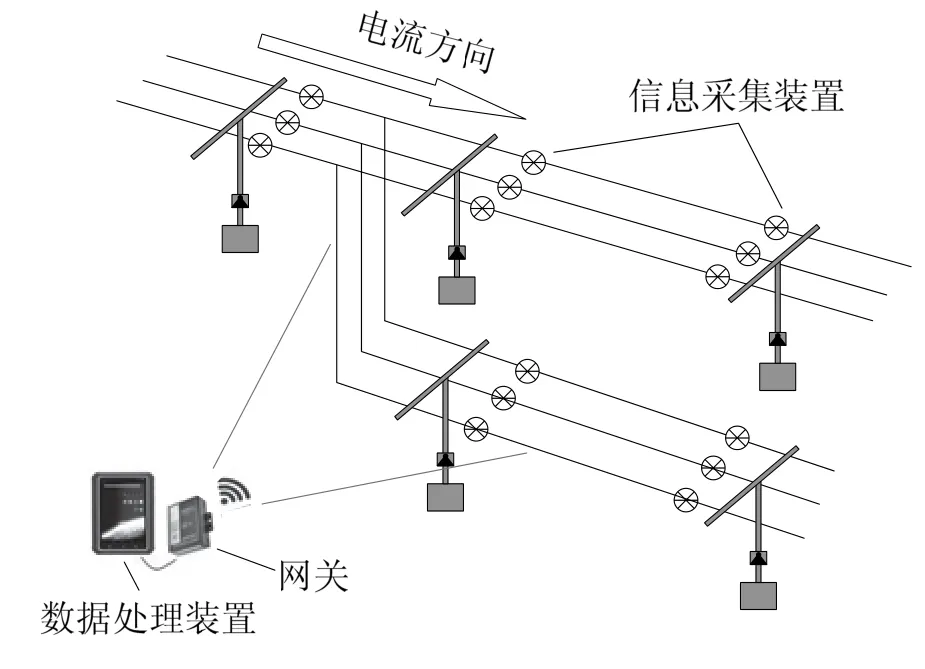
图4 线路采集装置安装示意图
以某多股道站场为例(图5),在每条线路的A、B两点右侧,C~E点左侧分别安装电流采集装置,根据线路始、末两端的电流差,判断发生短路故障的股道。
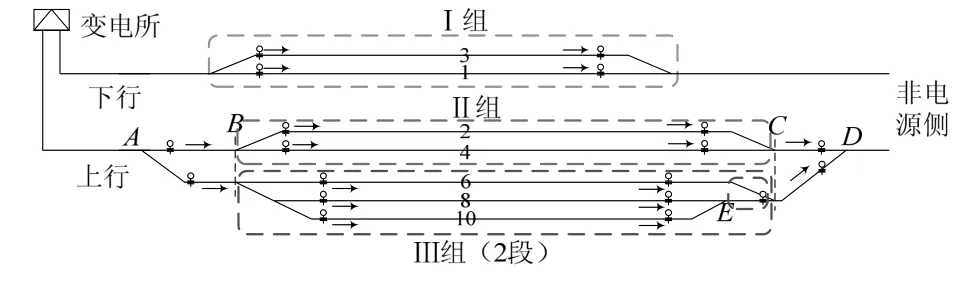
图5 多股道站场接触网示意图
对于分岔点B左侧的电流方向,可根据B点右侧的2个采集装置进行判断,若通过B点右侧的采集装置得到的电流之和与A点测得的电流之差满足要求,则说明AB段发生故障。确定故障点是否在交汇点C、E右侧两段的方法与AB段类似。
确定故障点所在股道后,通过电流比值得到故障距离,综合股道信息与距离计算信息得到故障点所在位置。
2 站场股道故障测距
2.1 直供牵引网故障测距原理
根据不同工况和不同短路方式选择不同的测距原理,目前常用的故障测距方法的原理及其适用场合见表1[6~8]。

表1 故障测距原理及适用供电方式
从表1可以看出,电抗测距法和上下行电流比法均适用于对带回流线的直供牵引供电系统的站场进行故障测距。
目前,对于直接供电系统牵引网故障测距普遍采用电抗法[9]。电抗法相对其他方法更简单可靠,但存在测距精度不准的问题[8]。上下行电流比法是通过下行馈线电流与上下行馈线电流之和的比值进行测距[6],该方法只适用于复线条件且分区所并联供电模式,多用于AT供电方式下的T线、TF线故障。由于多股道站场线路复杂,仅依靠上下行馈线电流无法实现对多条线路的故障测距,但是可以通过类似方法对多个点的电流进行测量、比较,实现故障测距。
综上分析,本文以上下行电流比法[6]为基础思路,提出通过股道的电流比值实现多股道站场故障测距的方法。

2.2 电流比值法测距
针对带回流线直供方式的多股道站场,可通过线路电流之间的比值关系进行牵引网故障测距。本文以某站场接触网(图5)为例,假设所有线路均为均匀传输线,对多股道站场进行故障测距计算。
某条线路发生短路故障时,故障点左右两侧电流大小相差较大,外部电流也会影响电流比值。规定电流流向以电流从电源侧(左)流向非电源侧(右)为正方向,线路发生故障时,线路右侧电流方向变为负向。假设图5—图8中所有电流方向均为正,由于电流总是从电源侧流向短路点,确定某条线路发生短路故障后,线路故障点右侧的电流是从线路右端流向故障点,与规定的电流方向相反,取负值。
图中,I01、I02表示外部电流,I11、I12、I21、I22、I2、I3、I42表示线路采集装置采集到的电流。
(1)2条股道一组。站场内某条线路发生如图6所示故障时,利用线路右侧电流减小外部电流I02对距离计算的影响,通过分析电流、电压关系得到

式中,Z0表示线路单位阻抗。线路发生故障时,I12、I02电流方向与图示方向相反,取负值。
化简式(5)得到故障距离为


图6 多股道线故障电路
(2)3条股道一组。与上述方法类似,当3股道一组的接触网发生线路短路故障①时,故障距离l可以通过任一非故障股道流过的电流计算得到。通过电流I21计算得到


图7 多股道线路故障电路
其中,I12方向与图示方向相反。
通过电流I3计算得到

其中,I12方向与图示方向相反。
由于故障线路不在对称轴上(故障点②),非故障线路上流过的电流I21和I3不相等,为减小误差,取计算结果的平均值作为故障测距结果,即

其中,I12方向与图示方向相反。
同样方法对故障线路在对称轴上进行分析,此时非故障线路I11=I3,可得到
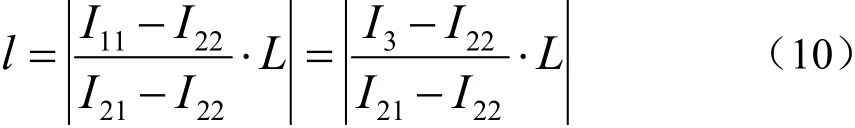
其中,I22方向与图示方向相反。
通过上述分析发现,3股道一组的线路无论故障线路是否位于对称轴,都可用式(11)进行故障测距计算,式中故障线路右侧电流取负值。

(3)股道末端交叉合并。图8所示站场只在点①发生短路故障,与本小节第(2)种情况所提到的计算方法类似,故障点①的位置可通过I21或I3计算得到,取2种计算结果的平均值作为测距计算式,从而减小测距误差:

式中,故障时I12、I02电流方向与图示方向相反,取负值。
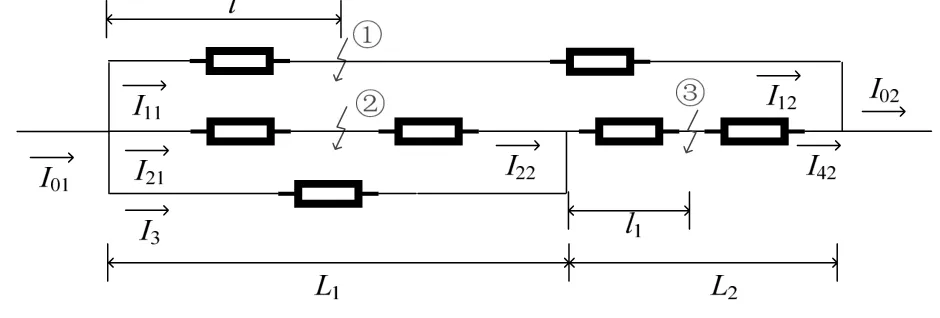
图8 多股道线路故障电路
当该站场上只在点②发生短路故障时,与上述计算方法相似,在此不做过多描述。
该站场上只在点③发生短路故障时,方法同上。此时I42、I02电流方向与图示方向相反,取负值。由于该组线路不对称,需要通过不同计算数值求取平均值得到故障点位置:
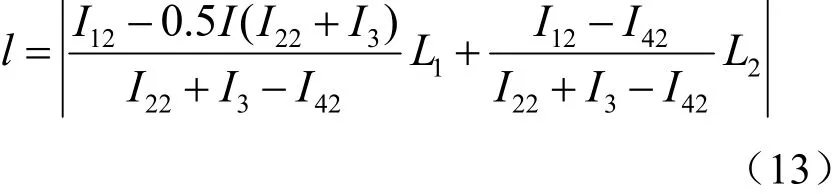
本节通过对多种类型的多股道线路进行分析、计算,当站场某组股道接触网发生故障时,选取对应的计算方法实现较高精度的故障测距。
3 故障测距原理仿真
本文以某多股道站场模型(图5)进行故障测距方案的研究,并搭建该站场Simulink仿真模型。
该站场接触网线路各段长度参数如表2所示。

表2 接触网线路距离 m
根据表2看出,AB、EC两段中的2条股道相邻,需考虑线路间的互阻抗;A、B两点相距不超过200 m,只需判断该股道上是否发生短路故障,不需要进行故障测距;CD段所涉及的2条股道相距较远,长度在100 m以内,无需考虑线路间的互阻抗,也不用进行故障测距的计算。
根据股道分岔、交汇位置不同可将该站场牵引网分为3组:Ⅰ组(下行1、3股道)、Ⅱ组(上行2、4股道BC段)、Ⅲ组(上行6、8、10股道BE段、上行8股道EC段)。
该站场的牵引网阻抗参数如下:
(1)双线路并联阻抗参数:
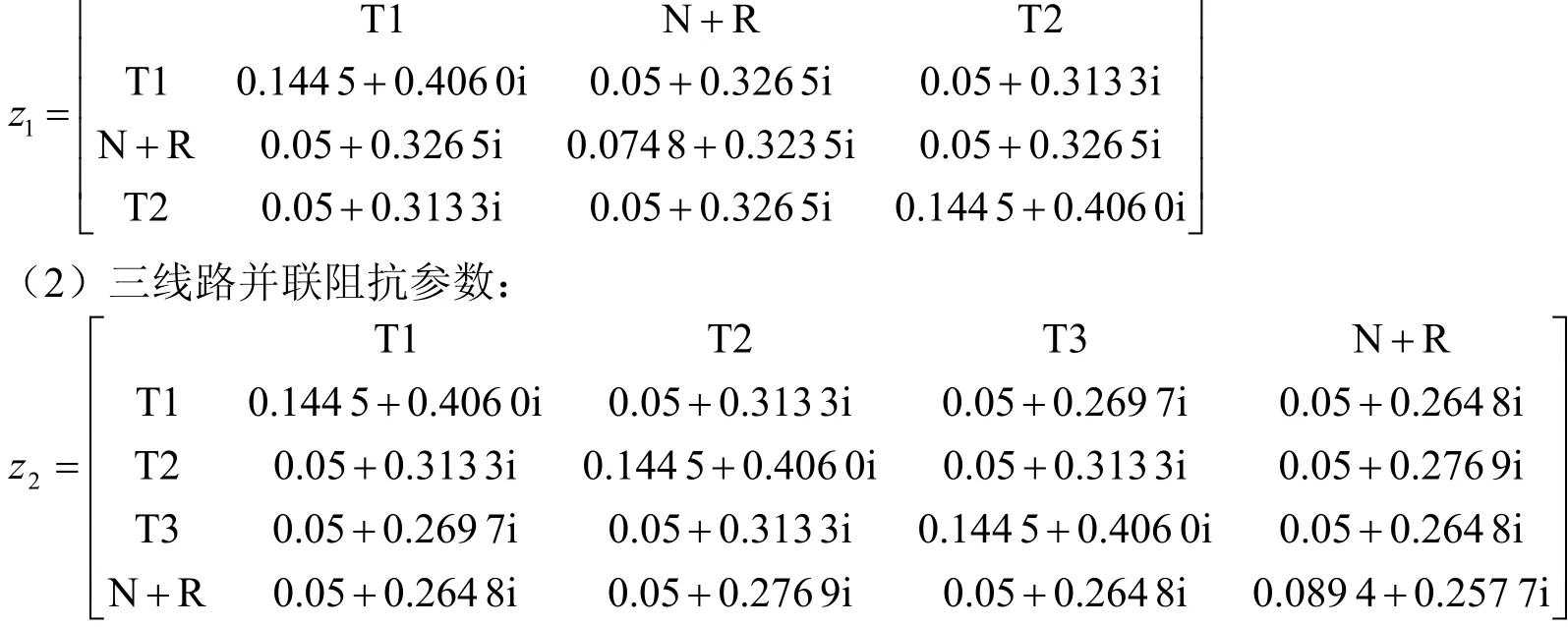
根据站场牵引网阻抗参数搭建Simulink仿真模型,对多股道站场的故障测距方法进行验证。
站场故障测距流程见图9。通过电流差值判断出故障点所在股道后,根据该组股道的模型选择相应的故障测距原理,调用该组股道的短路电流信息进行故障距离计算,最终定位故障点。下文以表格形式列出多股道站场故障测距的仿真结果。
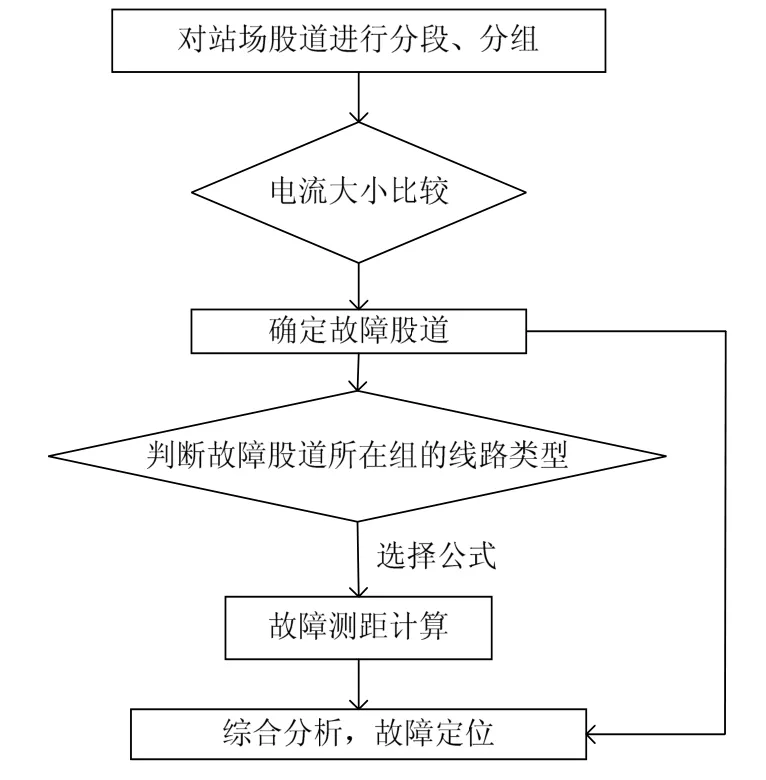
图9 站场故障测距流程
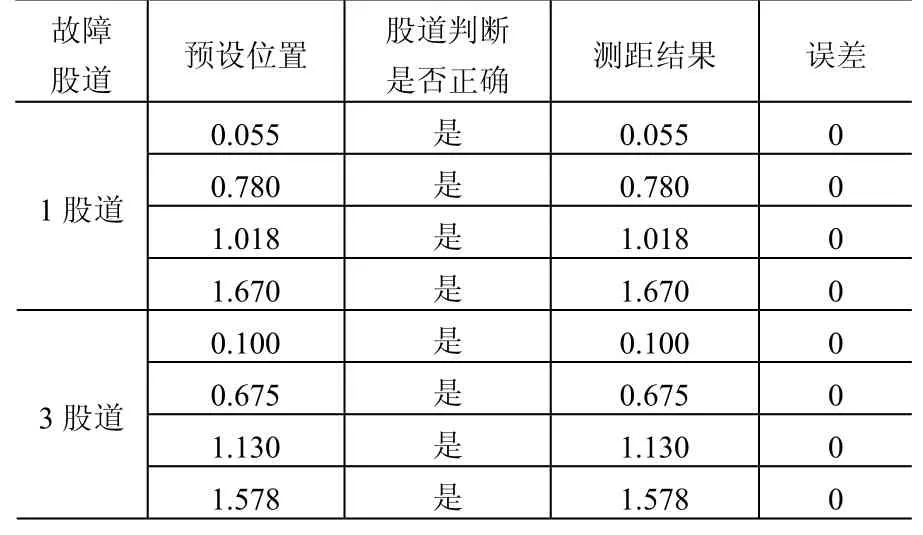
表3 Ⅰ组股道故障定位仿真结果 km

表4 Ⅱ组股道故障定位仿真结果 km

表5 Ⅲ组股道故障定位仿真结果 km
通过仿真发现,大部分故障测距误差在10 m以内,故障点靠近线路左端时,最大误差在50 m左右,小于线路长度的5%。目前工程上对于几公里到几十公里的线路,故障测距精度要求在500 m米或10%以内。本文研究的站场模型虽然距离较短,但误差在线路长度的5%以内,因此可以认为本文所提出的故障定位方案效果较为理想。
对于部分故障点的测距误差为0的情况,其主要原因:(1)线路较短,且仿真模型相对理想,不存在外界环境对测距结果的影响;(2)数据单位为km,计算结果只保留小数点后3位,经四舍五入后认为误差小于1 m的为0误差。
结合仿真结果和上述分析发现,可以通过电流比值法进行多股道站场故障测距,且该方法对于带回流线的直供站场的多股道故障测距方法来说,精度较高,在100 m以内。
4 结语
本文针对带回流线的直供牵引供电系统的多股道站场牵引网提出故障定位方案。从信息采集装置安装、故障股道判断和电流比值法测距3个方面进行研究,将上述3项内容组合,针对站场牵引网具体线路选择相应的计算模型,最终实现站场牵引网的故障测距。通过仿真模型的模拟发现,在多股道站场模型中,利用同一组线路的电流进行比值运算,得到的测距误差较小。本文通过对站场牵引网模型研究,提出的故障定位方案可大大提高多股道站场牵引网故障的测距精准度,缩短故障抢修时间,进一步保障了铁路的运输安全和通畅。

