大型浮船坞浮态鲁棒控制分析

董明海， 韩晨健， 赵 陈， 郭永升

(1.浙江国际海运职业技术学院，浙江 舟山 316021；2.中国船级社 舟山办事处，浙江 舟山 316052；3.上海船舶工艺研究所 舟山船舶工程研究中心，浙江 舟山 316021)

0 引 言

鲁棒控制涉及众多领域，涉及线性系统、时变系统、非线性系统、分布参数系统、离散系统等，作为鲁棒控制技术研究模型基础的线性分式变换(Linear Fractional Transformation,LFT)所能表示的不确定系统也十分广泛。不确定性不仅包含参数不确定性，而且包括噪声、扰动、非线性、未建模动态特性等丰富内容。目前，通常以状态方程中系数矩阵的线性摄动作为出发点，即认为不确定性与状态方程的系数矩阵呈线性关系，然后以此为基础进行控制系统的鲁棒分析与设计，但在实际问题中参数与状态方程系数矩阵之间的关系并不总是呈线性关系。浮船坞的设计主要依据各船级社的相关规范[1]。浮船坞在海上停泊或作业时，受到风浪流的干扰产生横摇，浮态控制系统目的在于抑制风浪流干扰，减少坞体横摇，控制浮态，确保其安全。以 30 000 t 举力浮船坞为例，采用鲁棒控制系统分析与设计方法，对其浮态的控制系统设计和鲁棒控制设计进行分析。浮船坞如图1所示。

图1 浮船坞

1 举力浮船坞概况

30 000 t举力浮船坞为整体式钢质浮坞，箱形船体，艏艉船底斜切，承载甲板无脊弧有梁拱，方形舭部钢质焊接结构。坞墙由顶甲板+骨架、内外坞墙+骨架、安全甲板+骨架、横向舱壁+骨架以及垂直桁等构件组成。 整个坞墙均为纵骨架式。由横舱壁及垂直桁组成横向强肋骨圈，共设有32 个压载水舱、2个污水舱和2个污油舱。其主要用于 30 000 t 及以下的船舶维修，入级中国船级社(CCS)。在遮蔽海域应用时，船坞可用于托举船舶作业，其构件的外形尺寸及重心高度应满足CCS规范关于浮船坞的稳性与干舷的相关要求。该坞主尺度如表1所示。

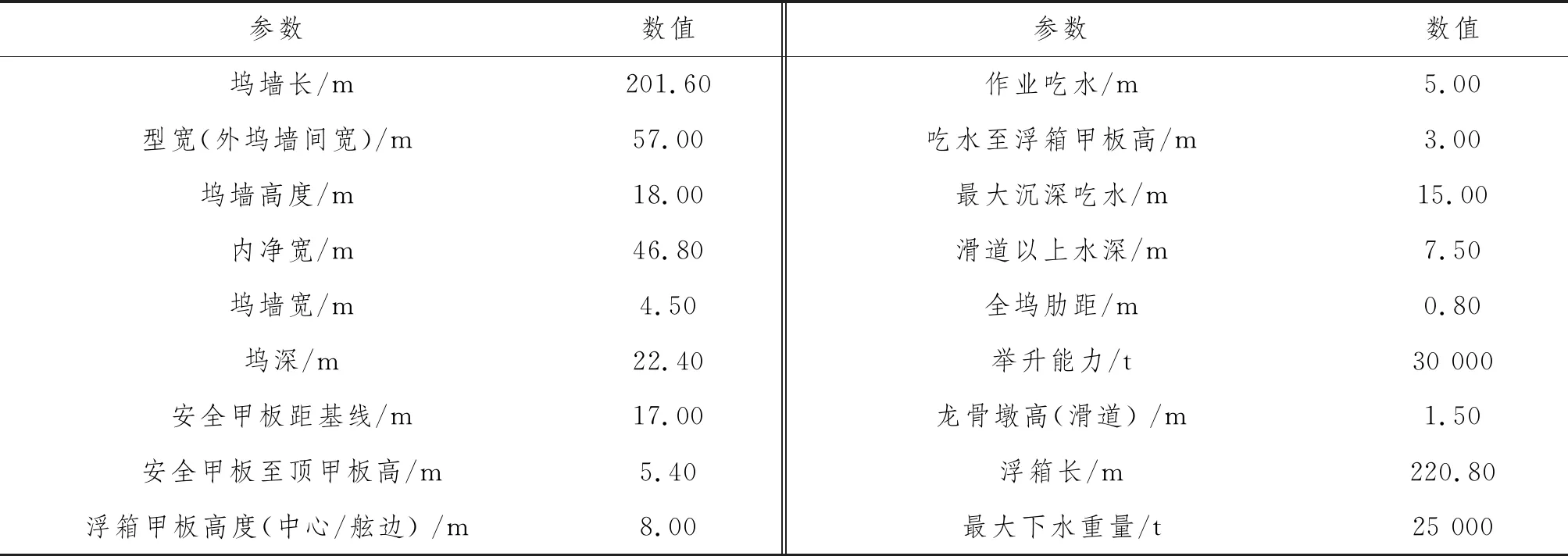
表1 浮船坞主尺度及主要参数

2 举力浮船坞浮态鲁棒控制设计思路

2.1 设计思路

浮船坞浮态控制系统的设计基于敏感度极小化的思想进行[2-3]，可分成3部分：坞体机械组合体、随动系统和控制部分，具体组成如图2所示。

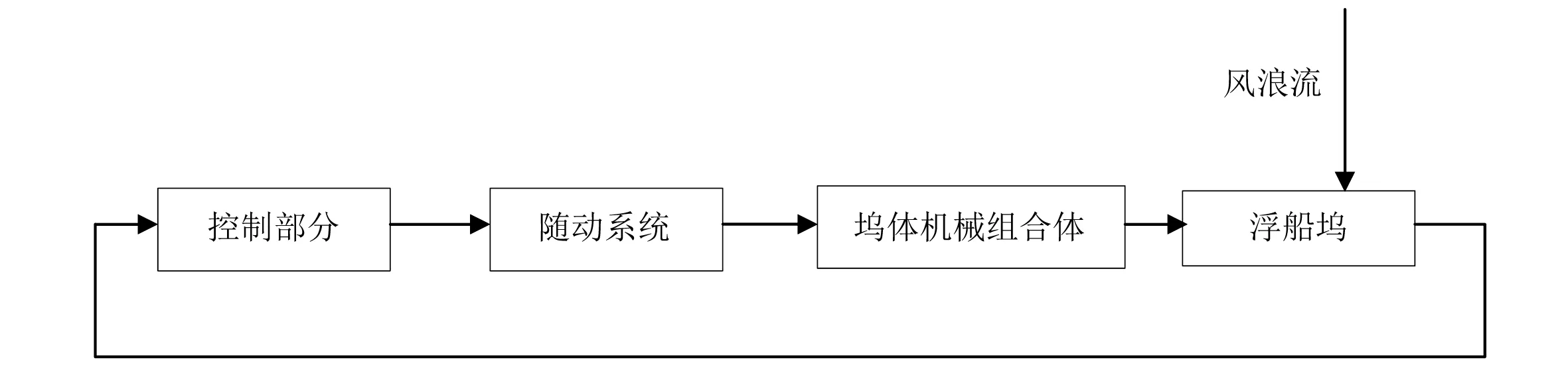
图2 浮态控制系统组成

根据灵敏度函数S设计典型反馈系统，控制部分具有较高输出灵敏性和准确度，灵敏度函数计算式为

(1)

式中：G为浮船坞的横摇传递函数；K为控制器，目标系统下为定值。

假定系统受到的不确定外干扰信号不是一个固定的信号，而是某个已知信号集合：

{d∶d=Wx,x∈H2,‖x‖2≤1}

(2)

式中：d为风浪流干扰信号；W为经验系数；x为振变量；H2为目标函数取得最优控制的极值。设计要求在信号集合中最坏干扰信号d的作用下，使系统在控制器的作用下输出能量‖y‖2最小。由于y=Sd=WSx，因此这一要求等价于

(3)

式(3)即转变为使加权灵敏度函数的极值范数极小化。由于敏感度函数S是开环特性的相对偏差到闭环特性相对偏差的传递函数，因此极小化S也可以使闭环特性的偏差抑制在尽可能小的范围内。设计控制器K，使闭环系统稳定且加权敏感度函数WS的极值范数极小化。

2.2 浮态控制系统

在利用灵敏度极小化问题化作极值标准控制(见图3)进行浮船坞浮体控制系统设计中会先遇到输入干扰抑制问题[4]。为解决这一问题，引入系统模型转换方法，将浮船坞控制系统的输入干扰转换为输出干扰，再转换为极值优化问题的标准形式，以求解具有输入干扰的极值优化问题，具体做法是利用系统方框图的等效原则，通过转换将浮船坞浮态控制系统的风浪流输入干扰转换为广义风浪流输出干扰，这就使外界干扰以等效的浮船坞横摇角的形式出现。

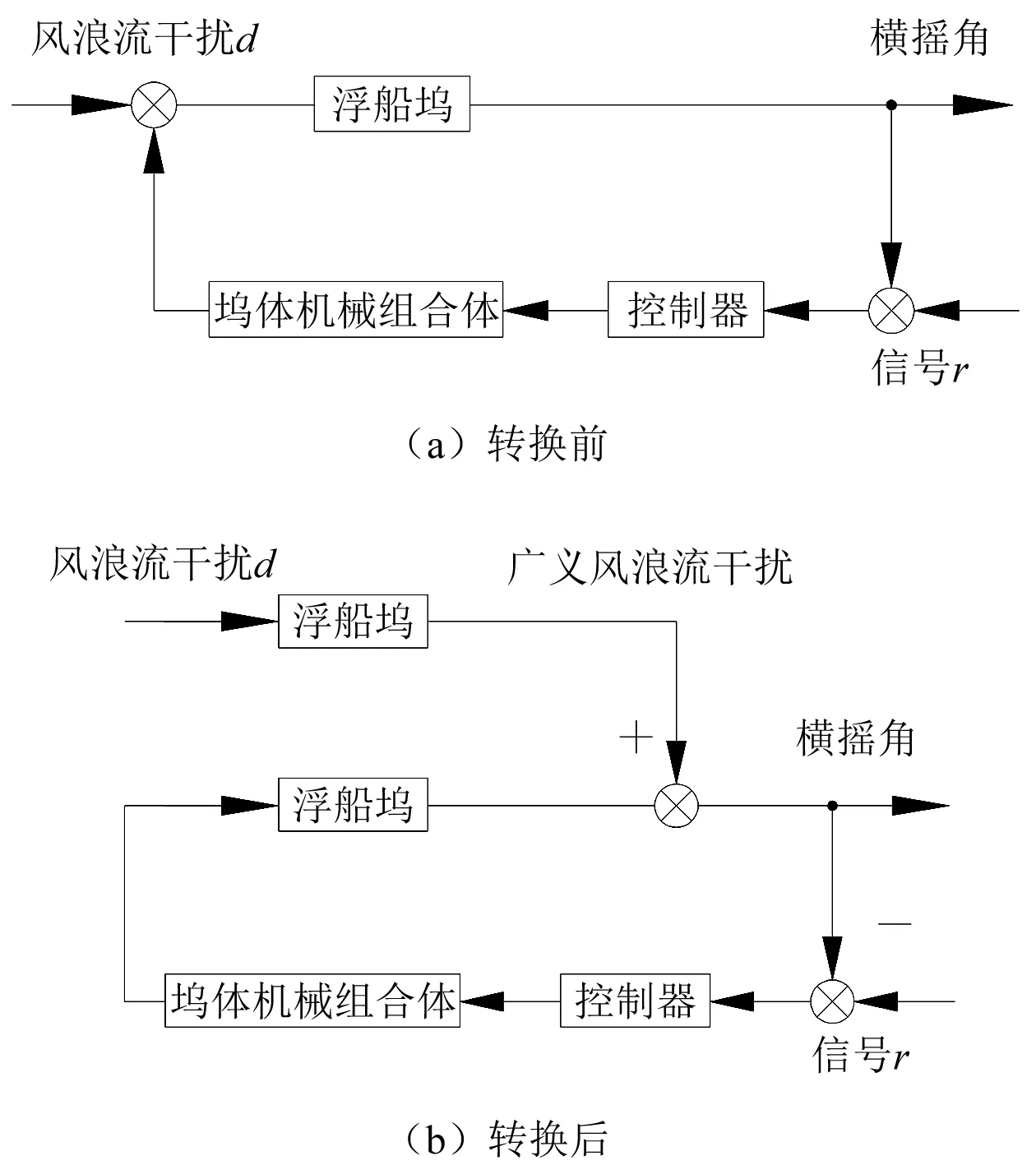
图3 模型转换前后的浮船坞浮态控制系统

设定坞体机械组合体传递函数为h，浮船坞的横摇角为φ，则根据控制理论，可求出横摇角φ对风浪流干扰的灵敏度函数

(4)

设定GK、GB分别为从参考信号r到横摇角的开环横摇传递函数和闭环横摇传递函数，ΔGK为相应真实开环横摇传递函数与标称开环横摇传递函数的偏差，ΔGB为相应真实闭环横摇传递函数与标称闭环横摇传递函数的偏差，则可推导得

(5)

可见，S与开环特征相对偏差ΔGK/GK到闭环特性相对偏差ΔGB/GB的增益1/(1+KhG)只相差1个标称的船体本身的横摇传递函数。因此，极小化S不仅反映了对风浪流横摇干扰的抑制要求，而且反映了抑制模型振动对系统的影响要求。

极小化横摇角φ对风浪流干扰d的灵敏度函数S的极值范数，既可达到抑制风浪流干扰的减摇目的，又可使闭环特性偏差抑制在尽可能小的范围内。

3 鲁棒控制设计

以30 000 t举力浮船坞为研究对象，其主要参数如下：排水量D为25 000 t，固有横摇周期T为11 s，初稳心高h1为5.409 m，无因次阻尼2Nu为0.28，横摇转动惯量Ix为65 564×104kg·m2，横摇附加惯量ΔIx=850×103kg·m2。其中，横摇附加质量是按切片理论计算波浪频率0.35～2.17共28个频率点的附加质量平均值。

浮船坞横摇运动方程式为

(6)

式中：C为作用在坞体上的横摇力矩。

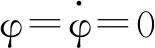
(7)

在坞体机械组合体的作用下，作用在坞体上的横摇力矩包括风浪流的干扰力矩Cw和压载系统产生的稳定力矩Cf，即

C=Cw+Cf=Cw+Cfaα

(8)

式中：Cfa为支撑力矩；α为浮船坞法线与水平面的夹角。

从而得到浮船坞在坞体机械组合体包括系泊设施作用下的线性传递函数为

(9)

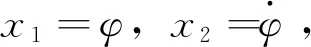
(10)

式中：

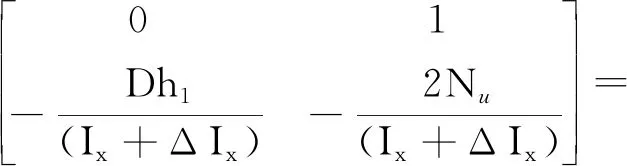
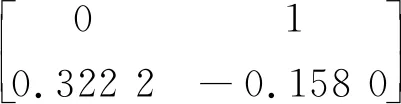
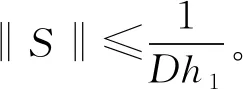
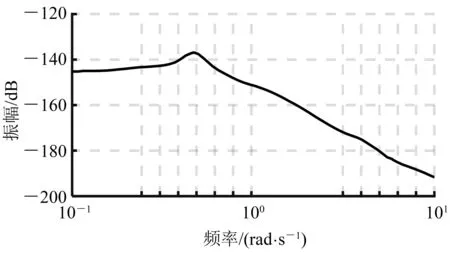
图4 浮船坞横摇频率特性

浮船坞的横摇特性是二阶振荡环节，在频率ω=0.57 rad/s时有1个谐振峰，浮船坞在该频率处放大横摇。风浪的能量主要集中在0.30～0.57 rad/s的频段内，在ω约0.70 rad/s时达到极值，因此，随机风浪流的主要作用频带和浮船坞横摇传递函数的频带相当。在选择横摇角φ对风浪流横摇干扰d的灵敏度函数S的权函数时，考虑到海浪能量谱特性，同时考虑坞体横摇特性在0.57 rad/s处有谐振峰，所选择的权函数应使S在谐振区内有大幅度的衰减。权函数须根据物理意义经反复地选择校核才能够最终选定[6]。

4 系统仿真

对直接基于灵敏度函数极小化思想设计的浮船坞横摇减摇控制系统进行仿真，检验上述分析与设计，为了使仿真具有代表性和充分反映各种外载荷情况，海情有义波高取值5.2 m，浪向角为30°、60°、90°、120°和150°，给出控制器的浮船坞横摇减摇控制系统的仿真结果数据分析，如表2所示。在表2中：开环和闭环的STD(φ)为横摇角的均方差；STD(αf)为减摇控制系统均方差；减摇率为开环横摇角均方差与闭环横摇均方差的差占开环横摇角均方差的百分比。

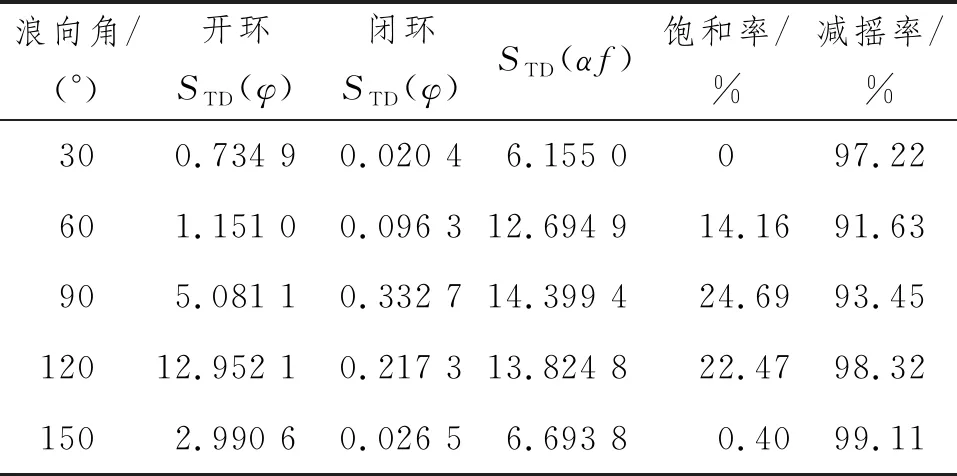
表2 不同浪向浮船坞横摇仿真结果统计(有义波高5.2 m)

当有义波高为5.2 m时，开环、闭环横摇角在不同浪向角下的仿真曲线如图5～图14所示。

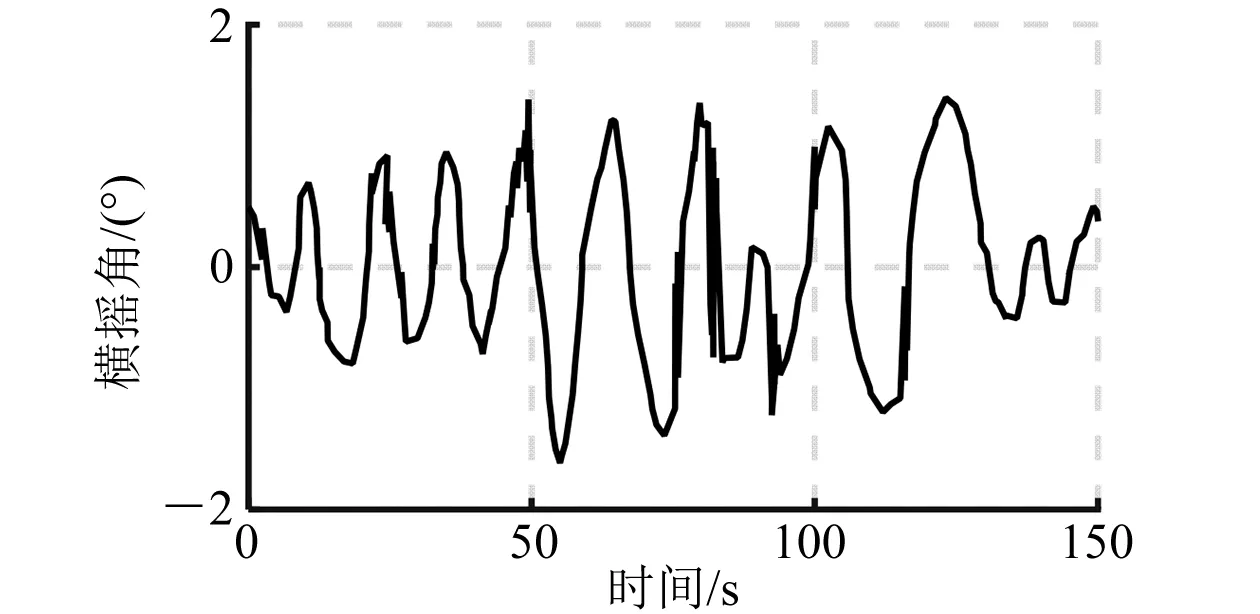
图5 开环横摇角仿真曲线(30°)

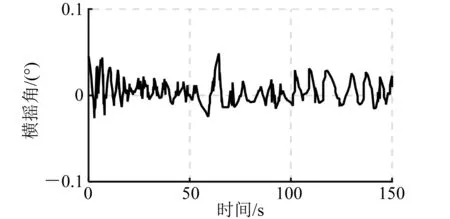
图6 闭环横摇角仿真曲线(30°)

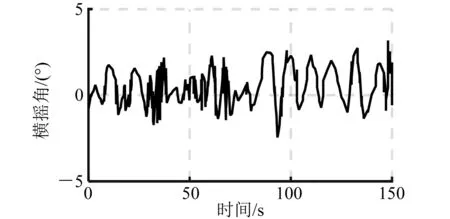
图7 开环横摇角仿真曲线(60°)

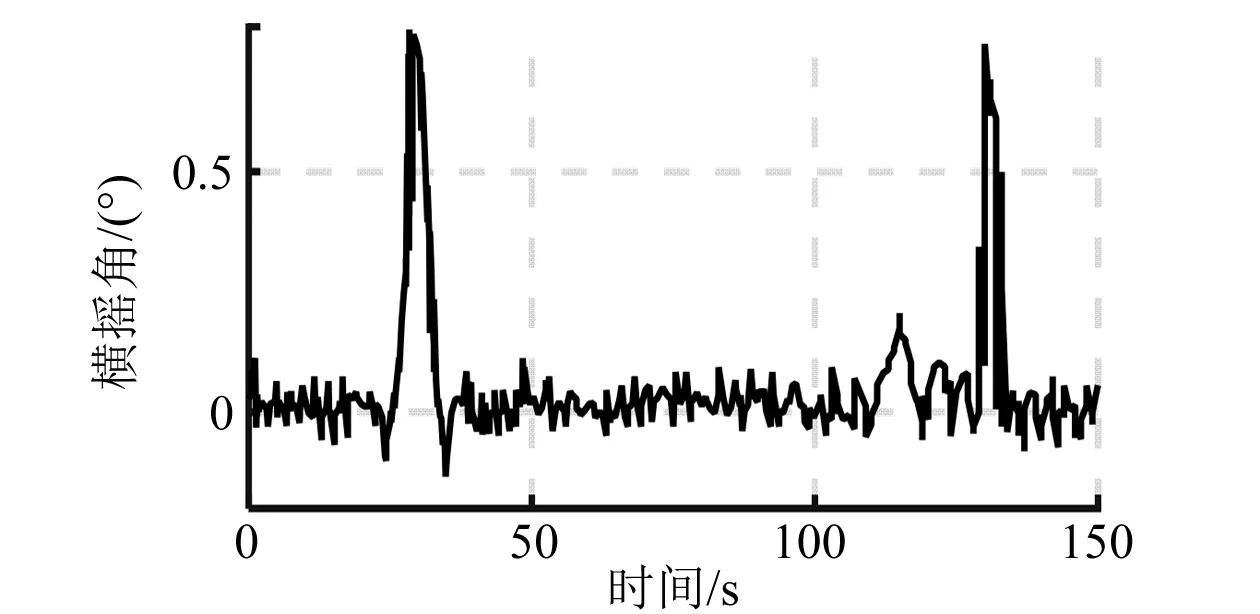
图8 闭环横摇角仿真曲线(60°)

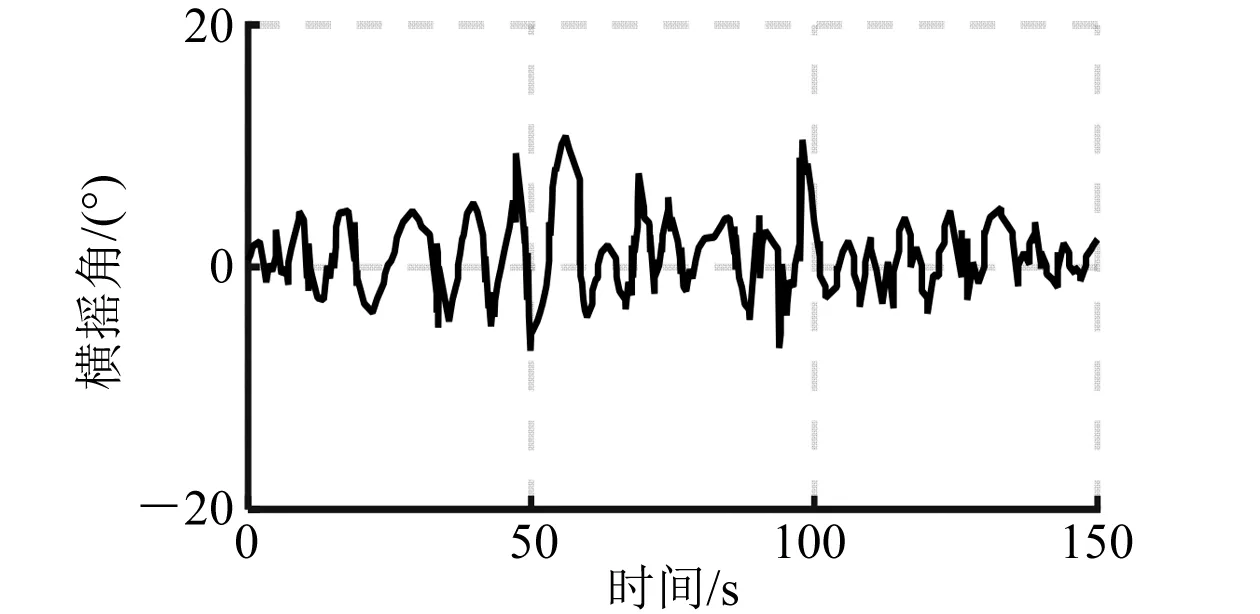
图9 开环横摇角仿真曲线(90°)

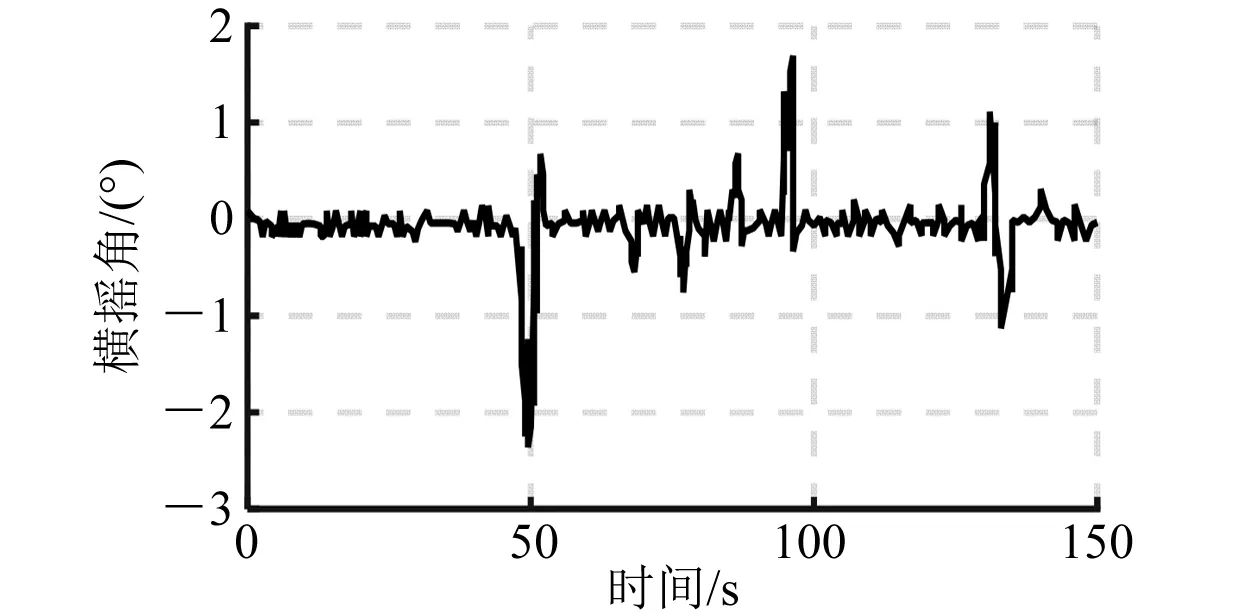
图10 闭环横摇角仿真曲线(90°)

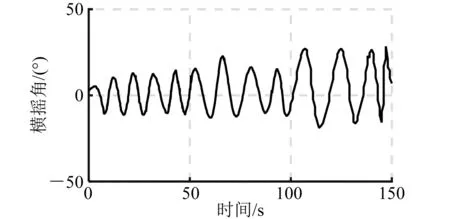
图11 开环横摇角仿真曲线(120°)

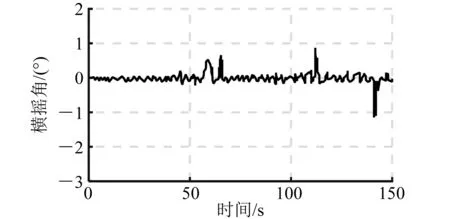
图12 闭环横摇角仿真曲线(120°)

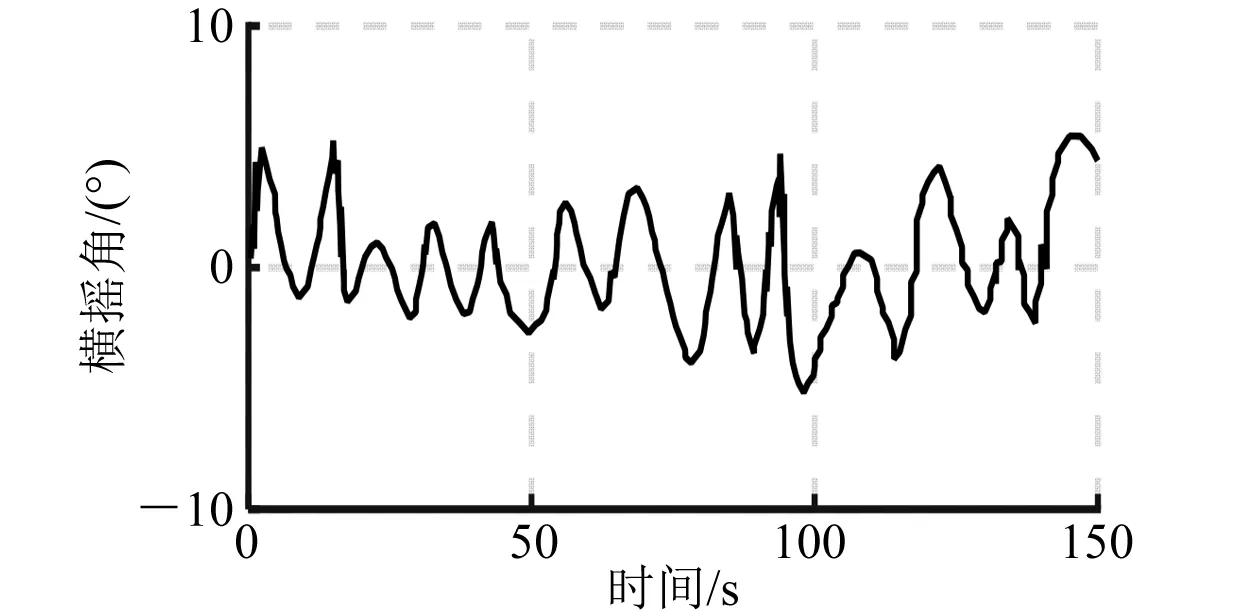
图13 开环横摇角仿真曲线(150°)

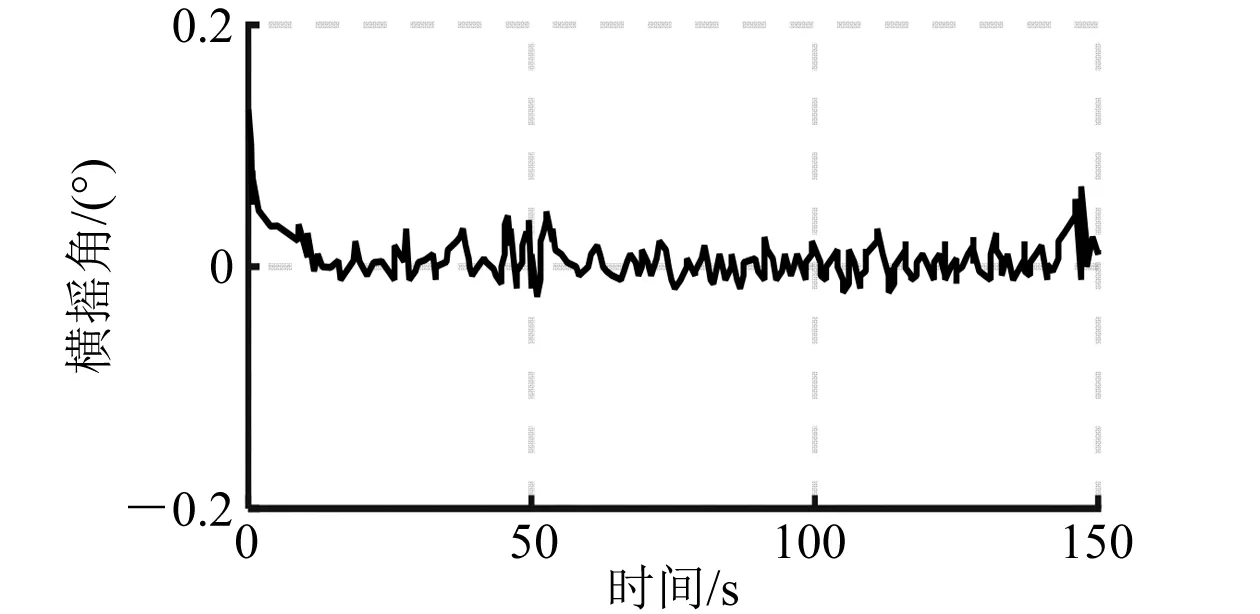
图14 闭环横摇角仿真曲线(150°)

由上述仿真曲线和数据分析可以看出：利用H∞理论设计的浮船坞横摇减摇控制器，在有义波高5.2 m不同浪向角下，都能很好地抑制随机海浪对浮船坞浮态的影响，有效减少横摇。

5 结 语

30 000 t举力浮船坞在控制器的控制下，降低对海浪干扰的抑制要求，这样的目的是为浮船坞压载系统和系泊系统联合减摇做准备。由于浮船坞本身运动的特性，风浪流对浮船坞的横摇运动影响较大，给出鲁棒控制系统的设计方法，采用模型仿真与运动参数仿真，结果充分证明该系统具有良好的鲁棒性，可为大型浮船坞系泊设计、压载水系统设计和浮态控制、检测等提供一定的参考。