全栈式机器学习在钢铁流程智能制造中的应用

肖 畅,吕立华

(宝山钢铁股份有限公司中央研究院,上海 201999)

1 概述

钢铁产品在炼钢连铸到加热炉再到热轧、冷轧等一系列生产过程中,经历了复杂的物理化学变化,在全流程生产中,各个工序积累了大量的高频生产数据以及对应的产品质量数据信息,这些数据信息具有量大、维数高、信息冗余、信息缺失、类别不平衡等特点[1-3]。在海量的生产信息中往往蕴含着产品质量的关键特征,这些特征信息的有效挖掘与应用,可以极大提高产品的质量与生产的降本。北京科技大学的吕志民等提出了一种统一架构的冶金全流程工艺质量在线和离线分析诊断系统解决方案,利用传统统计模型建立了工艺质量预警与在线判定系统,为冷轧领域全流程质量追溯和分析提供了统一的平台[4]。通过数据科学获得的结论往往需要结合钢铁物理冶金学知识进行判断与指导,通过物理冶金原理与机器学习模型相耦合对钢铁流程数据进行知识蒸馏,是钢铁行业数据分析与挖掘应该注意的地方。东北大学徐伟从物理冶金学与机器学习算法融合的角度出发,提出了以物理冶金学为指导的机器学习方法,设计出了新型超高强不锈钢[5]。

目前在钢铁生产流程中普遍缺乏一套整体的基于机器学习的分析框架,从数据层的多源异构数据搜集与治理到模型层的各模型库的综合开发与调用,各个模块常常处于独立开发与分析的情况,因此出现了数据孤岛、关键模型黑箱等问题[6-8]。本文通过实际生产的海量数据与产品质量问题解决方案的积累,针对全流程数据分析方法与思想进行梳理、研发全栈式机器学习平台与模型,形成了一套具有鲁棒性和高精度的钢铁生产全流程多源异构数据分析框架。本文的全栈式机器学习平台与模型在长型材领域、连铸领域、冷轧领域具有广泛的应用并取得了较好的效果,通过对生产数据进行搜集整理与特征工程,应用平台中的算法库解决了线材生产中椭圆度超差的质量问题与连铸过程夹渣的质量问题以及冷轧领域的带钢跑偏问题。系统功能架构图如图1所示。

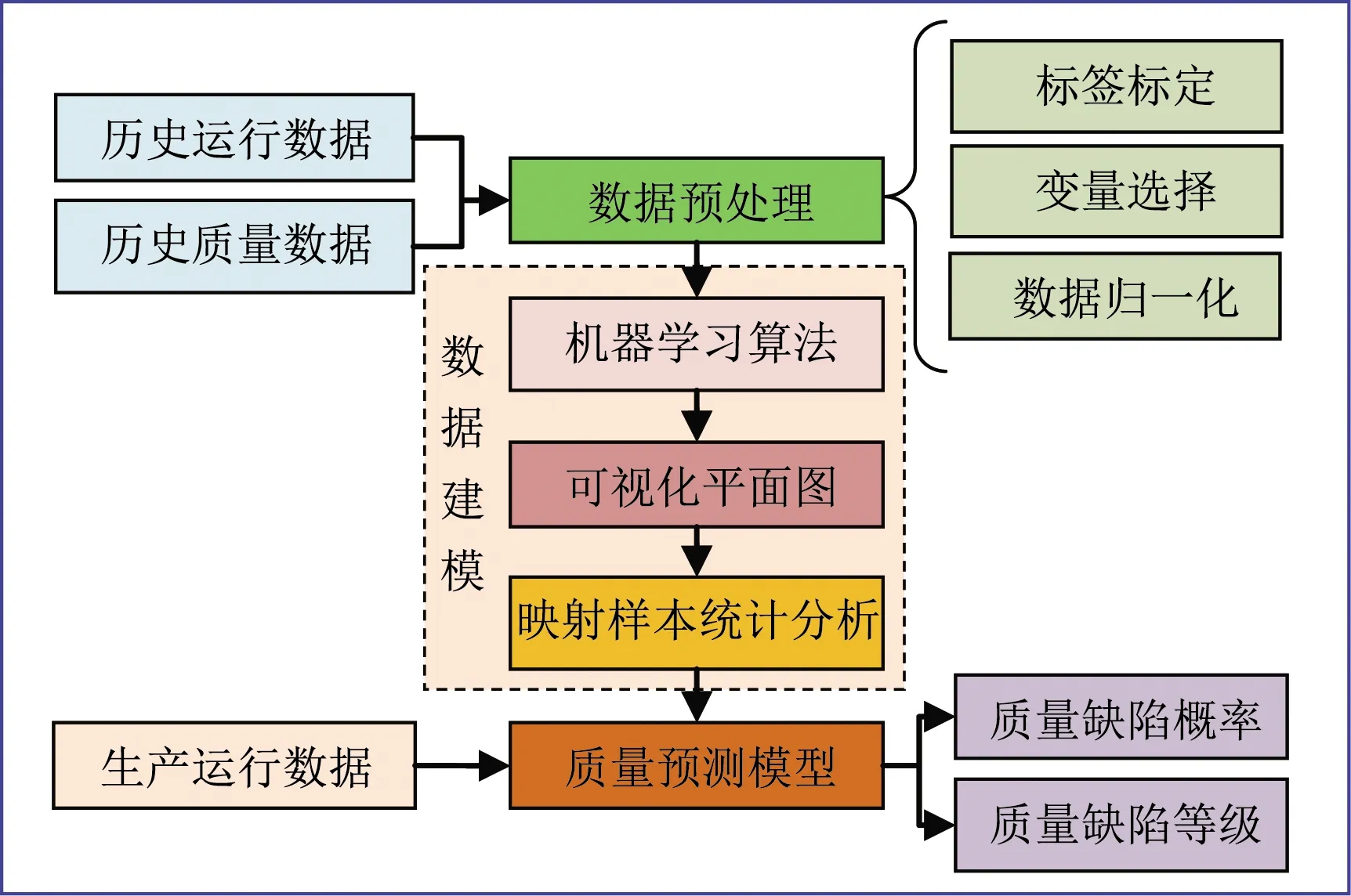
图1 系统功能架构图

2 工业数据分析框架

2.1 数据整合

钢铁流程生产过程中产生海量高频数据,同时对应的产品信息、质量信息、设备相关信息属于低频数据。钢铁全流程的工序较多,工艺复杂,涉及到数量众多的设备和传感器,受限于各种类型设备自身所特有的以及限定的数据格式与采集方式,传输类型不同,因此虽然钢铁流程生产过程紧密衔接,但是往往由于数据格式不统一,频率各异导致了“数据孤岛”的形成。全栈式机器学习具有平台支撑能力,从数据获取、清洗到模型建立、结果可视化的全栈式服务使得数据孤岛能够有效地被击穿。

全栈式机器学习平台的数据层应该具有多数据源兼容功能,包括主流关系型与非关系型数据库等,适配完善的api接口,支撑数据交互。除此之外平台还应具有完善的数据清洗、管理、校验等功能,包括支持字段映射、合并、拆分功能。

钢铁流程产生大量的时序数据,这些数据往往是高频采集信息,此类信息具有量大的特点,因此传统关系型数据库并不适合,往往挑选具有分布式存储功能的非关系型数据库,以及一些介于关系型与非关系型数据之间的数据库,例如MongoDB、BerkeleyDB、Redis等。标签信息、离散值信息等低频数据常常存储于MySQL、SQL sever等关系型数据库中[9-11]。

2.2 数据治理

由于产品质量异常并非连续的大面积的发生,因此在分析质量问题、异常溯因时往往面临异常标签数过少、类别不均衡的问题。在处理这类数据时,传统的机器学习在进行分类判别时总会倾向于多数类,而忽略少数类,由此导致机器学习效果大打折扣,使得整体性能恶化。目前针对不平衡数据集常常采取SMOTE 和 ADASYN(Adaptive Synthetic Sampling Approach)等过采样方法提高模型精度。

SMOTE算法通过线性插值,对邻域内样本进行处理从而生成标的样本。具体地,针对实际问题中的少数类样本xk使用k近邻法,计算出距离xk最近的k个少数类样本[12]。计算距离的定义为少数类样本之间n维特征空间的欧氏距离。然后随机地从k个近邻点中进行挑选,根据公式(1)对样本进行生成操作:

(1)

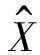
ADASYN算法是自适应综合过采样算法。该方法是通过对目标样本进行概率分布进行学习,通过自适应合成标的样本来减少样本的不平衡度[13]。算法流程如下:

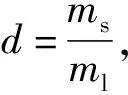
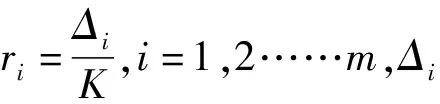
2.3 特征工程

钢铁全流程生产具有高维度的参数空间,在进行模型训练时,对变量进行挑选与降维十分必要。生产过程由于控制需求产生了大量的参数值,这些参数值往往具有冗余性和无效性与稀疏性,在进行变量挑选时,如果只依靠数据本身的特点来进行挑选,往往选出来的变量与生产实际中的物理常识有所违背,因此在进行变量挑选时,应该考虑数据的物理冶金学背景,在应用数学手段进行变换挑选后进行挑选与整理,并以此对模型参数进行调整,使得模型使用的变量最大程度地表征出整体数据中所蕴涵的规律与特征[14]。

实践中应用效果较好的变量选择方法有相关系数、最大相关最小冗余等方法。通过特征工程变量挑选结合物理冶金知识,挑选出的变量具有最大表征能力。相关系数法具有简单易用的特点,但是对于非线性关系,其表征能力就受到限制。最大相关最小冗余算法(mRMR)通过对候选变量进行重要性排序,实现冗余特征剔除,具有较好的鲁棒性[15]。

变量挑选后,获得重要性较高的变量集合,这些变量集合代表了影响产品质量的贡献度较高的操作参数集合。针对挑选后的变量空间,往往需要做进一步降维处理来提高数据的分类程度,工业生产中经常用到的方法有主成分分析(Principal Component Analysis)和Fisher线性判别(Fisher Linear Discriminant)等降维技术[16]。在钢铁流程生产中的质量问题一般都是具有标签值,因此有监督的Fisher线性判别法的应用效果更好。mRMR和Fisher线性判别法的算法介绍如下。

mRMR算法流程[17]:假设S为已选取的特征变量集合,该算法中集合S中所有特征的冗余是特征xi和xj之间所有互信息值的平均值,定义为式(2):

(2)

式中:I(xi;xj)表示xi和xj之间的互信息量;xi和xj表示不同特征;|S|表示集合的特征变量个数。

特征集S与类c的相关性由各个特征xi和类c之间的所有互信息值的平均值定义,相关性定义如式(3):

(3)

式中:c为标签,结合冗余度公式和相关性公式,得出算法的评价函数Φ(D,R),定义为式(4):

(4)

具体计算如式(5):

(5)

在实践中,用增量搜索方法求解Φ(D,R)。假设我们已有特征集Sm-1,我们的任务就是从剩下的特征X-Sm-1中找到第m个特征,通过选择特征使得Φ(D,R)最大。增量算法公式如式(6):

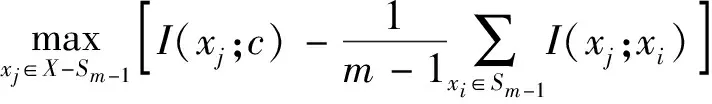
(6)

Fisher判别分析(FDA)算法流程[18]:假设存在X∈n·m,这些数据集被分成k类,ni代表第i类的样本点个数。类内协方差矩阵(Swithin)以及类间协方差矩阵(Sbetween)的定义见式(7)、(8):

(7)

(8)

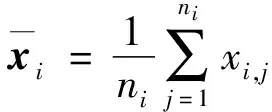
FDA算法优化的目标函数J的形式如式(9),寻找投影向量w使得J最大:

(9)

主要目的就是求解满足上面目标函数的彼此正交的向量解,把这些向量按照能够使样本类内方差最小、类间方差最大的原则从大到小排列好,组成一个向量集,即第二个 FDA 向量与第一个 FDA 向量正交,两个向量按照类内方差最小、类间方差最大的原则从大到小排序,第一个FDA向量在第二个FDA向量前面,其余的FDA 向量以此类推。于是满足条件的FDA向量就等于求解以下广义特征值问题的特征向量w,见式(10)。

λSwithinw=Sbetweenw

(10)

当求解出投影矩阵W以后,通过式(11)可以将高维数据转换到低维空间:

H=XW

(11)

2.4 模型选取与应用

工业生产中由于数据较为全面,质量问题具有标签,因此大部分问题都属于分类问题。分类算法中工业较为常用的算法有SVM、随机森林、XGBOOST等。本文限于篇幅限制仅对常用的XGBOOST模型机型进行介绍。

XGBOOST的全称是eXtreme Gradient Boosting,该方法是在GBDT的基础上对Boosting算法进行改进的,基学习器采取决策树模型。Boosting是一种有效的集成学习方法,可将弱分类器转化为强分类器[19]。

XGBOOST的算法思想是通过特征分裂来生长一棵树,每次添加的树是学习一个函数来拟合前一次的预测残差,样本特征在每棵树中会落到对应的一个叶子节点,一个节点有一个分数,最后将每棵树的对应得分相加就是该样本变量选择的结果。

算法步骤:

假设模型有k个决策树,即式(12):

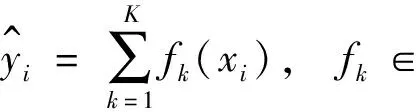
(12)

(13)

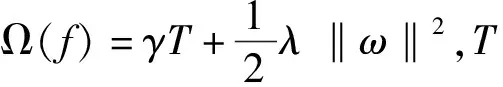
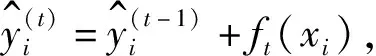
(14)

Boosting Tree模型采用加法模型与前向分步算法,开始于一个常数预测,每次增加的一个新函数学习当前的树,去拟合上一次模型拟合后产生的残差。

对损失函数进行二阶泰勒近似展开,式(15):

(15)

式中:gi和hi分别是一阶和二阶梯度统计。通过这种近似,就可以自定义损失函数,对式(15)进行常数项的移除,再将Ij={i|q(xi)=j}定义为叶子节点j中的样本集合,通过扩展惩罚项Ω(ft)重写目标函数如式(16):

(16)

(17)

GBDT采用的是分割标准最小化均方差,XGBOOST在此基础上进行了改进,采用的是从单个叶子节点开始,迭代地向树添加分支的贪心算法。假设IL和IR是分割后左右节点的集合,最终得到的分割后损失减少如式(18):

(18)

3 分析实例

钢铁生产的各个工序中存在着产品的各种质量异常,针对产品质量异常溯因与管控,利用物理冶金学知识进行处理往往需要设计较为复杂的实验,追溯周期长,管控精度往往不能得到保证。基于数据驱动的质量监控与溯源能够提高效率与精度,结合物理冶金学知识进行把控,能够快速准确地定位异常原因并使得模型与结果具有可解释性。

在长型材领域,线材产品的应用广泛,且作为国家国民经济建设的重要支柱性产品,产量多,技术含量高。线材产品的特点是生产速度高、变形剧烈,往往在产成品中存在着结巴、耳子、裂纹、椭圆度超差等缺陷。由于产线流程工艺复杂,利用机理模型解释往往精度不高,同时产线设备众多,影响产品质量的因素众多,同时由于生产速度快,往往在产成品端才发现质量问题,因此质量溯原困难[20-22]。

高速线材生产线具有数据采用点密集的特点,各种高频数据与特征数据都可以实时采集,具有典型的大数据支撑能力,因此本文基于全栈式机器学习,利用数据驱动,对质量问题进行溯源与监控。基于数据与物理冶金学的融合驱动,对高速线材产线中典型的质量问题进行分析。

3.1 数据样本获取

试验数据来自线材厂实际生产数据,选择2020年全年数据进行训练和测试。高线生产产线流程较长,分为粗轧机组、中轧机组、预精轧机组、精轧机组、减定径机组、斯泰尔摩等各个工序,各个工序又包含各自数量的轧机机组以及测温点、水箱等设备。为了尽可能覆盖全部生产信息,本文将各工序的生产数据总共133个生产参数作为输入,对椭圆度超差问题进行质量溯源与监控,响应变量为椭圆度超差。高速线材生产工艺见图2。

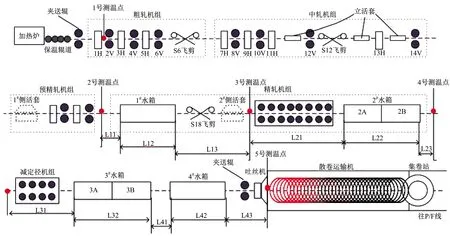
图2 高线生产工艺流程

本文基于全栈式机器学习平台,自动搜集与拼接多源异构数据,利用整合好的数据进行训练。针对生产中生产频率较高且容易出现椭圆度超差的6个钢种和规格数据,按照全栈式机器学习的步骤进行分析。

高速线材产生的数据规模年累计数据可达到TB级,其中高频时序数据存储于BerkeleyDB中,标签特征信息、产品钢种信息等存储于SQL server数据库中,在进行数据变量挑选、特征工程、建模预测时,按照条件进行选取配置即可。

3.2 数据样本治理

在实际生产中有些钢种产量大,椭圆度超差发生频率高,正常样本与异常样本数均衡,而有些钢种规格的椭圆度超差现象虽然发生频率不高,但是属于重点产品,质量问题出现会造成较大的损失,因此同样需要进行分析与监控,此时正常样本与异常样本数不均衡,属于类别不均衡样本,针对此类数据,应利用分析框架中针对类别不平衡数据的方法进行分析。本文选取的6个钢种对应的椭圆度超差样本与椭圆度正常样本个数对比图如图3 所示,钢种6的异常样本数明显少于正常样本数。

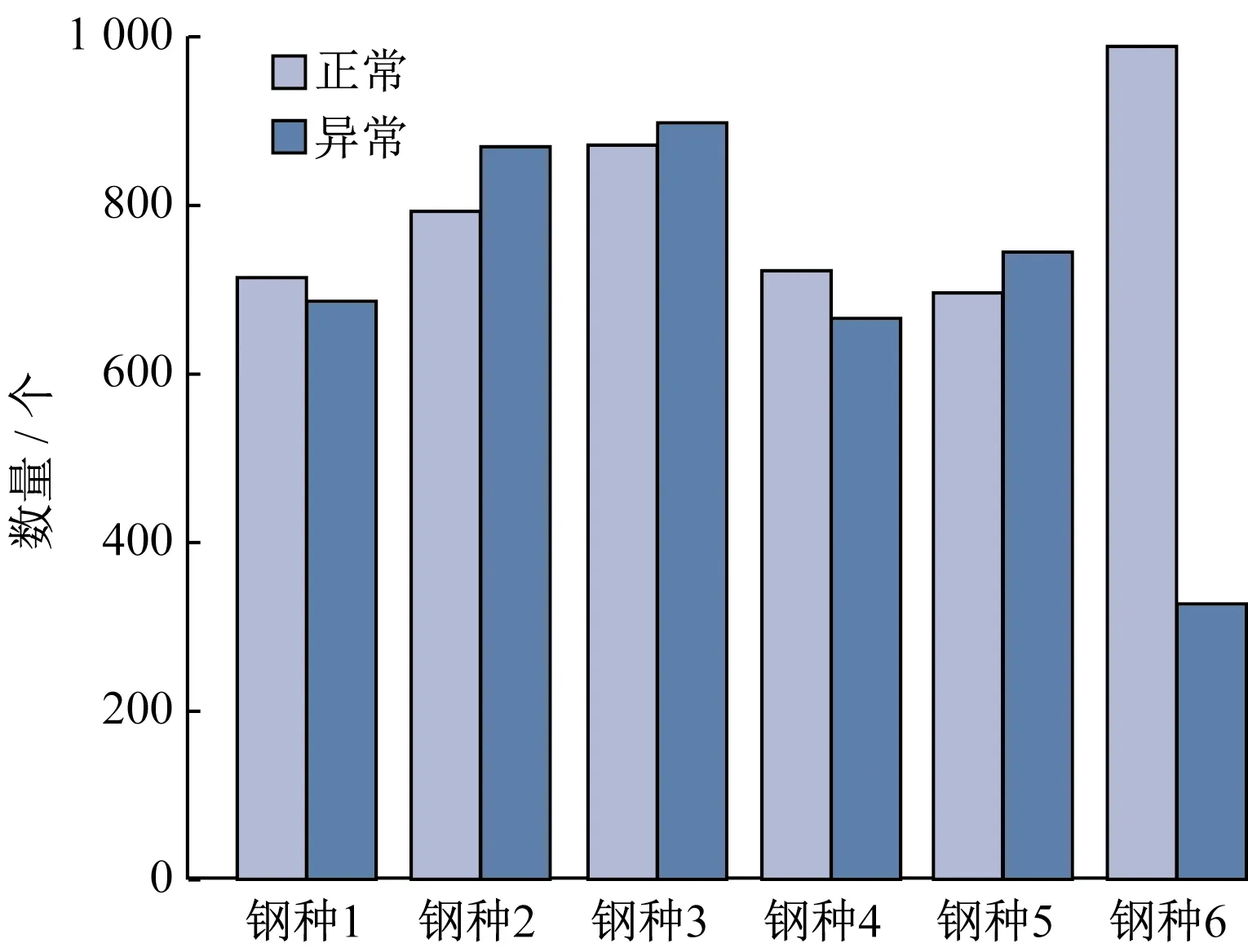
图3 各钢种样本量对比

钢种1至钢种5由于样本较为均衡,不用进行采样技术处理。针对钢种6采用SMOTE算法对样本进行处理,原始样本中正常样本个数为986个,异常样本个数为326个。经过SMOTE算法处理过后正常样本个数与异常样本个数相当,如图4所示。

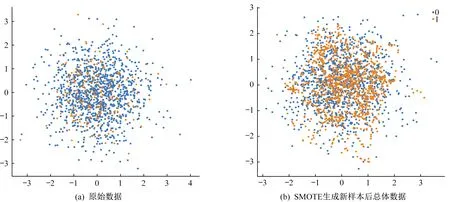
图4 数据总体分布图

3.3 特征工程

目前的操作变量有133维,如果不加选择都作为训练数据,那么模型将学到大量的无效信息,而且维数的增长也使得模型的复杂度显著增加。因此需要对数据进行特征工程处理,筛选出最有效的操作变量。本文将数据中的6个钢种混合在一起进行变量挑选,挑选出具有共性的操作变量,基于mRMR算法,对输入的133维数据进行变量筛选,最终结果按照重要性评分选取。选取重要性排前15的操作参数进行后续建模。重要性评分表见表1。

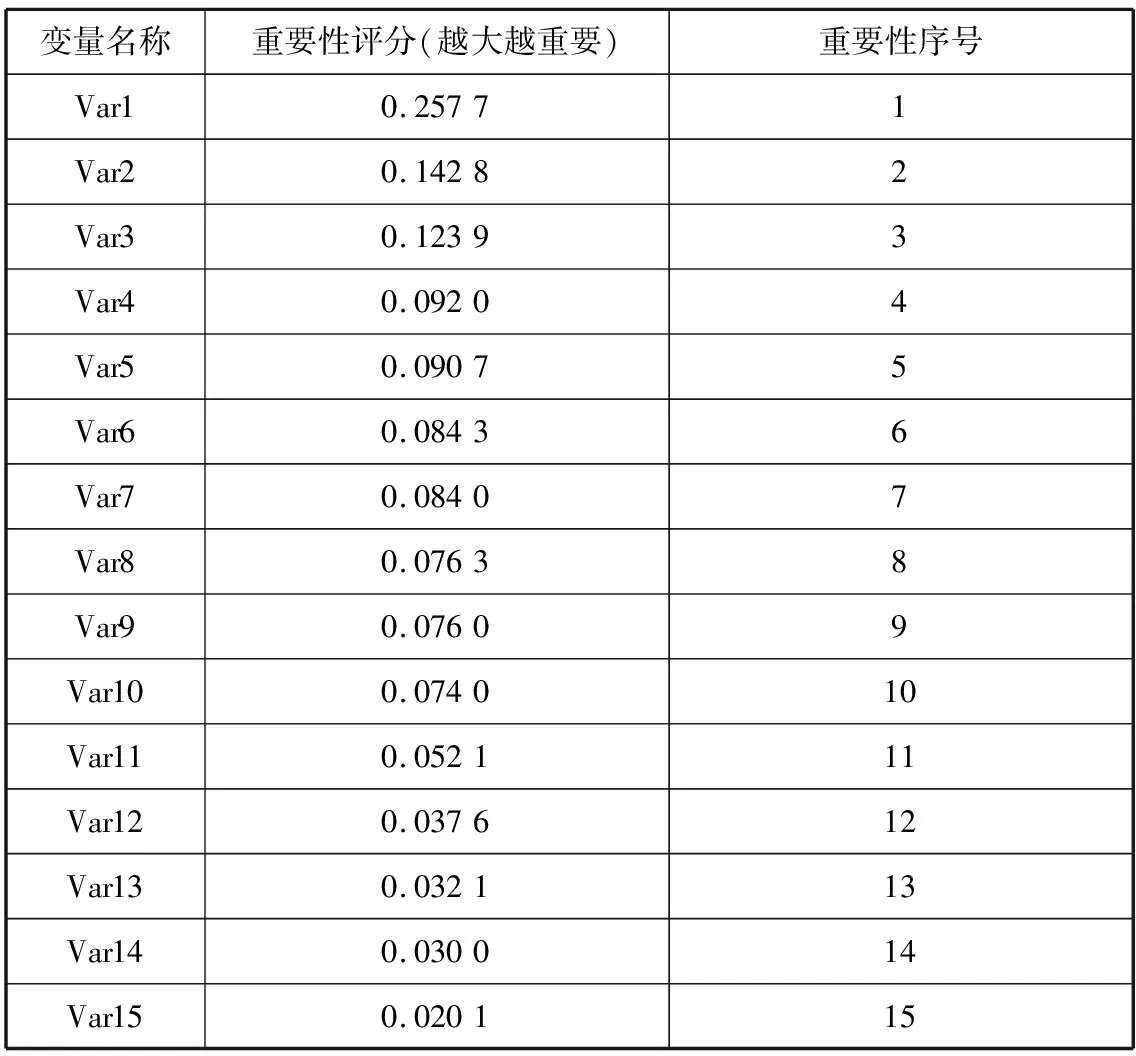
表1 相关特征的重要性排序

3.4 模型应用

本文应用全栈式机器学习中的Feature-XGBOOST模型进行椭圆度超差缺陷进行预测分类。根据mRMR算法的重要性排序结果,逐步剔除评分排在最后面的P个变量,基于选择出的变量,应用FDA进行有监督的降维,将数据进行投影,得到投影矩阵,将投影矩阵与数据集相乘,得到降维后的特征矩阵,将求得的特征矩阵应用于XGBOOST模型中,对椭圆度超差进行分类预测,随着P的变大,试验结果如表2所示。

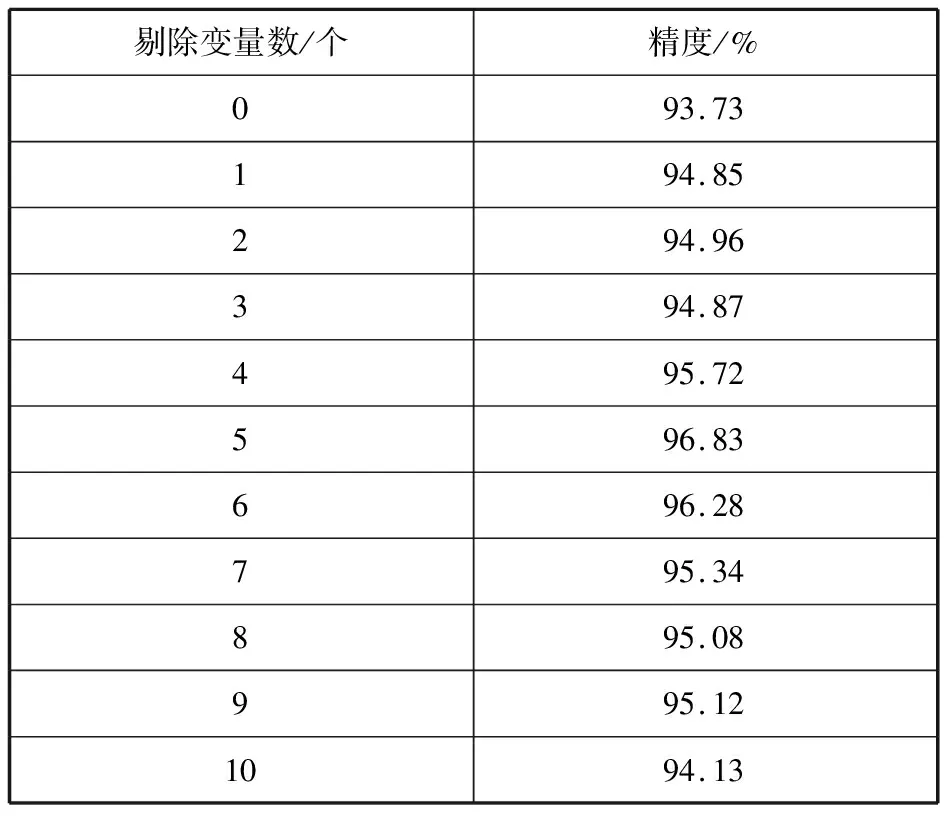
表2 Feature-XGBOOST预测模型精度变化

由表2可知,当剔除5个特征变量时,模型的预测精度最高,此时分类精度为96.83%。相比于不剔除任何变量而言,剔除5个特征变量后,精度提升了 3.10%,此时模型能更好地解释椭圆度超差异常和各变量之间的关系。

为了充分验证Feature-XGBOOST椭圆度超差分类模型的准确性,引入BP神经网络、SVM支持向量机等传统方法进行对比,对比结果如表3。

表3 不同算法模型检测精度对比

试验结果表明,BP、SVM等传统模型的分类误差较大,这是因为传统单个模型应用没有考虑变量的挑选与特征的选择,从众多输入变量中选出了代表性变量,筛除冗余或无关变量,提高了预报的准确性和实时性。

4 结论

(1)通过实际生产的海量数据与产品质量问题解决方案的积累,针对全流程数据分析方法与思想进行梳理、研发全栈式机器学习平台与模型,形成了一套具有鲁棒性和高精度的钢铁生产全流程多源异构数据分析框架。在钢铁流程生产中进行了应用。

(2)提出了工业数据分析的通用方法,针对质量问题,分析流程为:数据获取、数据治理、特征工程、模型选取与应用、问题解决。

(3)应用全栈式机器学习平台搜集数据,并应用平台中的算法库进行模型建立,基于mRMR算法进行变量挑选,应用FDA进行特征降维,并应用XGBOOST对数据进行分类,实现了质量问题溯源与监控,解决了线材生产中椭圆度超差的质量问题。