一种求解欧拉方程的高精度数值格式

任琴琴,白晓雅,郑秋亚,梁益华

(1.长安大学 理学院,陕西 西安 710064; 2.中国航空计算技术研究所 航空气动力数值模拟重点实验室,陕西 西安 710068)

计算流体力学(computational fluid dynamics,CFD)需要借助计算机完成,随着计算机技术的飞速发展,CFD的理论基础和实际应用得到了快速发展。双曲守恒律方程经常被应用在流体力学等实际问题中。众所周知,即使守恒律方程的初始条件是光滑的,方程的解也可能产生间断,如激波、接触间断波等。激波捕捉的计算格式是计算流体力学的常用工具,这些格式常用于模拟流体力学中出现的各种现象;对大量格式研究发现,高阶激波捕捉格式具有较好的计算效率。目前,加权本质无振荡(weighted essentially non-oscillatory,WENO)格式是一类应用广泛的激波捕捉格式,是近几年求解双曲守恒律方程常用的数值方法之一。

文献[1-2]提出了总变差递减(total variation decreasing Runge-Kutta,TVD-Runge-Kutta)的概念;文献[3]证明了TVD-Runge-Kutta格式在接近光滑极值的情况下最多具有一阶精度;文献[4-5]导出了具有放宽TVD-Runge-Kutta条件和允许在数值格式中出现伪振荡性质的高阶格式,被称为本质无振荡(essentially non-oscillatory,ENO)格式;文献[6]在有限差分框架下构造ENO格式;文献[7]提出了有限体积框架下的WENO格式;文献[8]在有限差分框架下提出了经典的WENO格式,简称WENO-JS,该格式在多维空间上建立了局部光滑因子和非线性权重;文献[9]对WENO-JS进行分析发现,在临界点处并未达到最优精确阶,利用映射加权公式提出了一种改进的格式,即WENO-M格式;文献[10]进一步改进,提出了一种含有全局光滑因子的非线性权重,构造WENO-Z格式,数值实验表明这种格式主要是对传统的WENO-JS格式中非线性权重的改进,减小了数值耗散,同时提高了分辨率,避免了像WENO-M格式在临界点附近精度的损失;文献[11]将这种思想推广到高阶格式,提出了一种全局光滑因子的广义公式;文献[12-13]通过引入一种新的基于拉格朗日插值的局部光滑因子η,构造WENO-η格式;文献[14]基于L1范数提出了用于五阶WENO格式的新光滑因子,称为WENO-NS格式,该格式将一阶导数的高阶近似引入到全局光滑因子,相对于其他WENO格式,WENO-NS格式的全局光滑因子是由五点模板和中间三点模板的光滑因子的平均得到的;文献[15]导出了七阶WENO-NS格式,并用广义不可分差分算子得到了光滑因子,通过引入参数ζ来平衡光滑区域与间断区域之间精度,由此得到的全局光滑度指标满足在存在临界点的情况下得到最优收敛速度阶的充分条件。

迎风格式因其物理意义清晰、分辨率高,至今仍是空间离散的主要格式之一。为了达到较高的计算效率,并且在间断处达到高分辨率,文献[16-18]提出对流迎风分裂(advection upstream splitting method,AUSM)格式;文献[19-20]提出对流迎风和分压(convective upwind and split pressure schemes,CUSP)格式;文献[21-24]表明,CUSP格式根据其对流项的总能量是总焓还是总能，分为总焓对流迎风和分压(total enthalpy convective upwind and split pressure schemes,H-CUSP)格式、总能对流迎风和分压(total energy convective upwind and split pressure schemes,E-CUSP)格式。2种格式计算过程中均避免了矩阵运算,提高了计算效率。E-CUSP格式数值耗散小,分辨率高,能清晰地捕捉激波剖面和精确的接触间断。

本文在空间上采用基于E-CUSP格式与七阶的WENO格式耦合得到新的格式,捕捉间断,实现高精度,时间上采用文献[25]提出的四阶TVD-Runge-Kutta格式来推进。

1 控制方程

1.1 欧拉方程

考虑一维双曲守恒律方程:

(1)

1.2 E-CUSP格式

在区间单元上利用有限体积法,得到方程(1)的数值离散形式:

(2)

E-CUSP格式的主要思想就是将通量分解为守恒型通量和压力型通量两项。该格式值耗散项的系数不是矩阵而是标量,避免了矩阵运算所带来的时间消耗,可以减少计算量,提高计算效率。(1)式中的F雅克比矩阵可表示为:

其中

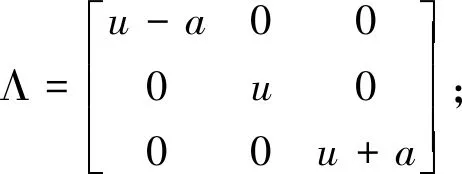
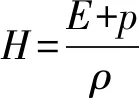
由F和A之间的齐次性可以得到如下关系:

F=TΛT-1U

(3)

根据雅克比矩阵的特征值的特性,将(3)式拆分为:

其中,Fc=u[ρ,ρu,E]T、Fp=[0,p,pu]T分别为守恒型通量和压力型通量。

守恒型通量Fc可表示为:

(4)

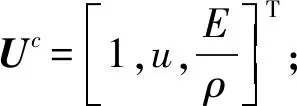
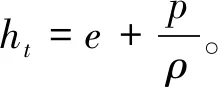
在压力型通量Fp中,动量方程中压力的表达式为:

(5)

能量方程中的压力可分解为:

(6)

最终E-CUSP格式中通量F可表示为:

(7)

其中:a为音速;M为马赫数。

2 数值方法

2.1 WENO-JS格式数值重构

WENO格式用于评估变量UL和UR。采用qk的凸组合近似变量UL的WENO格式可以写成:

(8)

其中：qk(k=0,1,…,r)为不同模板中变量的重构多项式；ωk(k=0,1,…,r)为权重。

(8)式给出的重构形式既适合光滑流场也适合含间断流场。对于含激波的间断流场,(8)式中非线性权函数ωk的定义如下:

(9)

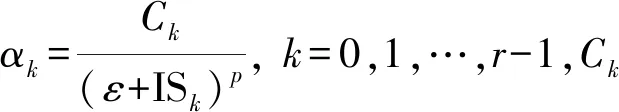
文献[8]提出的光滑因子ISk为:

(10)

2.2 WENO-Z格式数值重构

文献[10]通过引入全局光滑因子τ,重新定义了WENO-JS格式的非线性权值,并得到接近理想权值Ck的非线性权值:

(11)

其中

对于七阶WENO-Z7格式,全局光滑因子定义为τ7=|IS0+3 IS1-3 IS2-IS3|。

2.3 WENO-NS格式数值重构

WENO格式的基本要素是光滑因子的计算,文献[15]基于L1范数光滑因子建立了七阶高精度的WENO格式,称为WENO-NS7格式。因为基于L1范数的光滑因子在光滑区域可能会导致精度损失,所以该格式利用导数的高阶近似。

光滑因子的构造如下。

定义运算符Ls,kU,通过估计导数的近似值大小,测量每一个四点模板

Sk(j)={xj+k-3,xj+k-2,xj+k-1,xj+k},

k=0,1,2,3,

中解的规律性。得到这些算符后,光滑因子ISk的计算公式为:

ISk=ξ|L1,kU|+|L2,kU|+|L3,kU|

(12)

其中:ξ∈(0,1]为平衡光滑区域和间断区域精度之间的平衡的参数;算子Ls,kf为f的广义不可分差分,公式如下:

(13)

运算符L3,kU与WENO-JS7格式中的相同,但是L3,kU在WENO-NS7格式中使用绝对值,在WENO-JS7格式中使用平方值。

算子Ls,kU的优点是导数ΔxsU(s)在点xj+1/2处的逼近具有更高的精度:

WENO-NS7格式的非线性权重定义为:

(14)

其中

对于WENO-NS7格式,全局光滑因子定义为τ7=(IS0-3 IS1+3 IS2-IS3)2。

2.4 Runge-Kutta方法

对于欧拉方程在时间方向上的离散,本文使用文献[25]的四阶TVD-Runge-Kutta方法来解决等式:

(15)

其中,L(u)为导数-f(u)x的近似。

四阶TVD-Runge-Kutta方法公式为:

(16)

其中:Δt为时间步长;L(·)为差分算子。

3 数值结果与分析

为了验证本文E-CUSP-WENO-NS7格式数值模拟效果,针对具有Riemann初值问题的Euler方程,应用E-CUSP格式、E-CUSP-WENO7格式、E-CUSP-WENO-Z7格式和E-CUSP-WENO-NS7格式进行数值模拟,对比它们的结果,并将数值模拟结果与理论解进行比较,从而对其性能进行分析。

3.1 一维Euler方程修正的Sod激波管问题

本文在区域[0, 1]上求解初值问题:

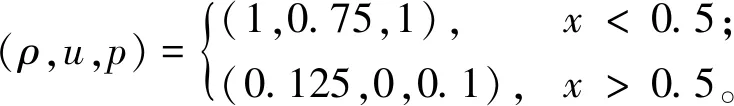
采用Neumann边界条件:

|λi(G(Δx,k))|≤1+cΔx

(17)

其中:λi(G(Δx,k))为增长矩阵G(Δx,k)的特征值;Δx为空间步长;c为常数。取CFL=0.1,空间取等距的200个网格点。

该问题的精确解主要由稀疏波、接触间断和激波构成,密度、速度和压力在t=0.2时用E-CUSP格式、E-CUSP-WENO7格式、E-CUSP-WENO-Z7格式和E-CUSP-WENO-NS7格式计算一维Euler方程激波管问题的数值模拟结果如图1所示。通过对图1及其局部放大图对比分析,可以看出,E-CUSP-WENO-NS7格式很好地捕捉到了激波和接触间断波。

3.2 一维Euler方程Lax激波管问题

本文在区域[0, 1]上求解初值问题:

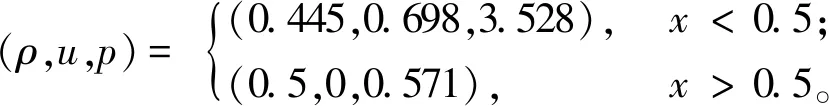
采用Neumann边界条件(17),取CFL=0.1,空间取等距的200个网格点。密度、速度和压力在t=0.16时用E-CUSP格式、E-CUSP-WENO7格式、E-CUSP-WENO-Z7格式和E-CUSP-WENO-NS7格式计算一维Euler方程Lax激波管问题的数值模拟结果如图2所示。通过对图2及其局部放大图对比分析,可以看出,E-CUSP-WENO-NS7格式在激波处的数值模拟结果优于其他格式,对激波的捕捉更为陡峭,具有较小的数值耗散。

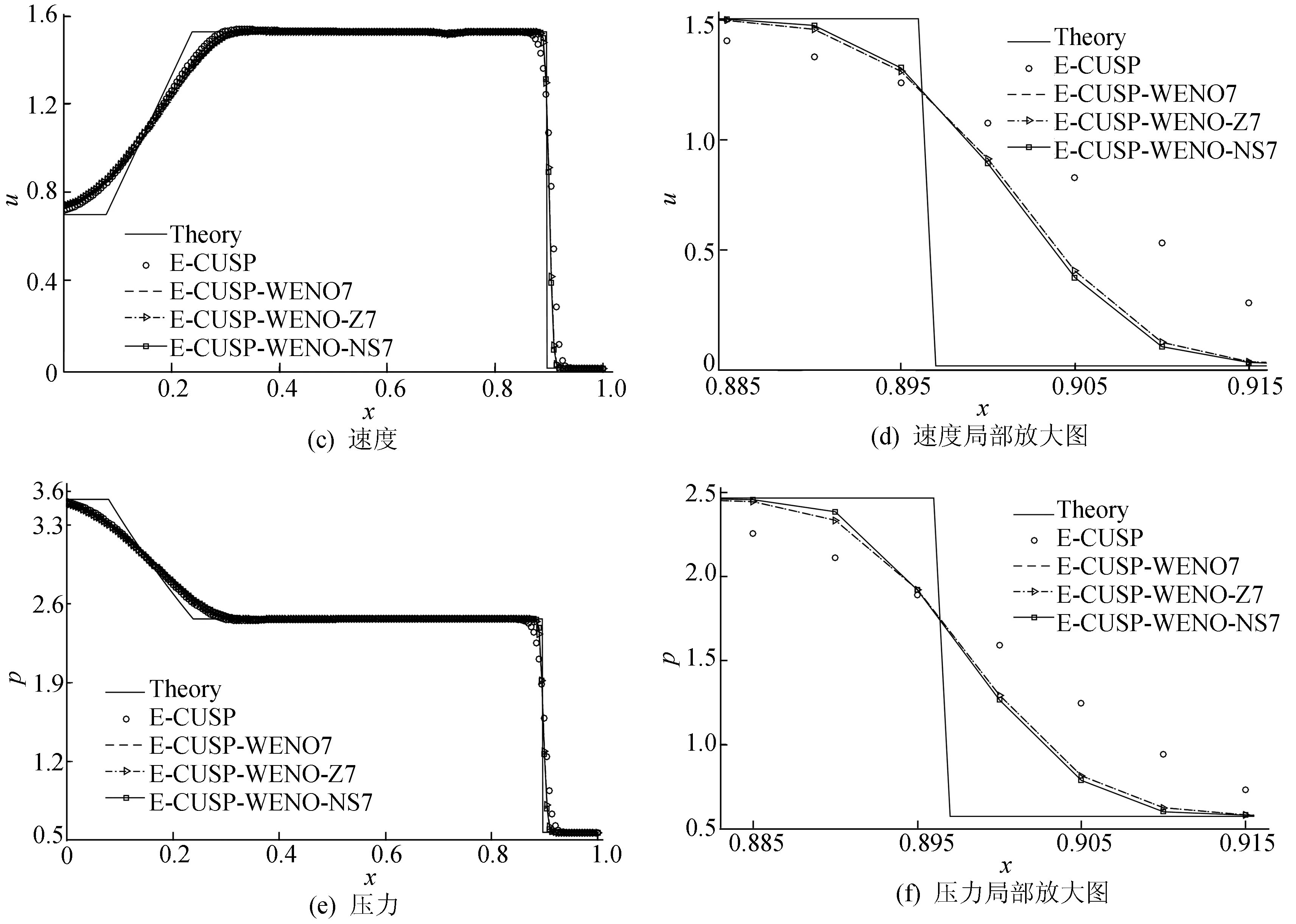
图2 一维Euler方程Lax激波管问题的数值解

3.3 一维Euler方程激波管问题

本文在区域[0, 1]上求解初值问题：

(ρ,u,p)=

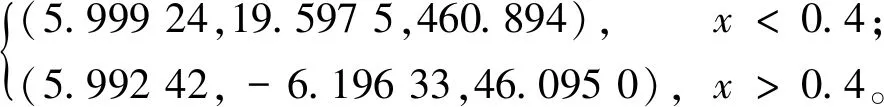
采用Neumann边界条件(17),取CFL=0.1, 空间取等距的200个网格点。

密度、速度和压力在t=0.25时用E-CUSP格式、E-CUSP-WENO7格式、E-CUSP-WENO-Z7格式和E-CUSP-WENO-NS7格式计算一维Euler方程Lax激波管问题的数值模拟结果如图3所示。

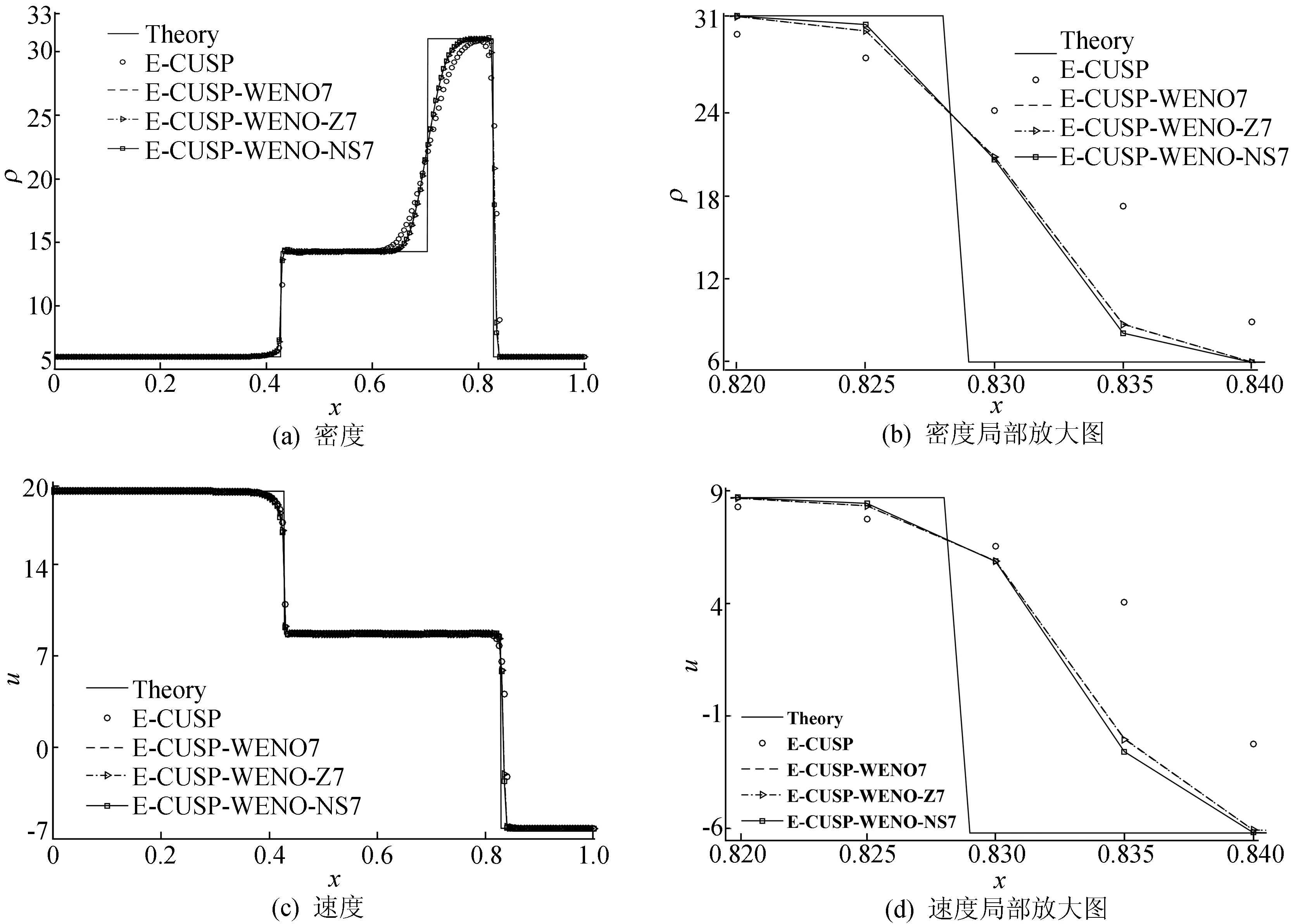
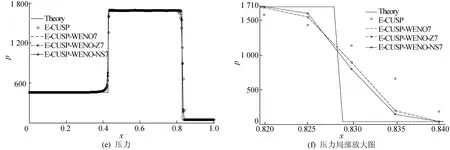
图3 一维Euler方程激波管问题的数值解

通过对图3中各局部放大图对比分析,可以看出,E-CUSP-WENO-NS7格式在激波处过渡带窄,而且对解的捕捉比其他格式更加精确,计算结果更接近理论值。

4 结 论

本文提出E-CUSP与WENO-NS7耦合格式:E-CUSP-WENO-NS7格式,逼近非线性双曲守恒定律的解,基于模板上插值多项式导数的不可分差分格式,构造局部和全局光滑因子。理论分析和数值实验结果表明,在相同网格情况下,与其他格式相比,E-CUSP-WENO-NS7格式对接触间断和激波的捕捉更为精确,分辨率更高,计算精度更高,数值耗散更小,新格式具有更好的稳定性。

接下来研究的方向是:将耦合的新格式与自适应阶结合提高计算效率,并应用到文献[26]所提到的海底输油管道石油泄漏和文献[27]提到的通风空调等实际问题中。