一种联合优化内容获取与容量的蜂窝关联方案

张文天,王禄生,林 海,方 超

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.武汉大学 国家网络安全学院,湖北 武汉 430072)

0 引 言

近年来,无线移动通信技术迅猛发展,第五代移动通信系统(5G)将达到更高的数据速率、更大的系统容量、更低的传输时延以及更好的服务质量。高密度网络是5G关键技术之一,通过在传统大功率宏蜂窝的覆盖范围内大规模密集部署低功率微微蜂窝和飞蜂窝,缩短终端与服务基站之间的“距离”以提升终端接入后获得的频谱效率和系统吞吐量[1];其次,随着智能终端的迅速普及,移动网络中多媒体业务的需求正以惊人的速度增长。然而,当前蜂窝网络的集中式架构会造成核心网拥塞程度增大与回程链路带宽偏小以致于难以应对移动通信流量爆炸式增长的问题,因此相关研究普遍认为应把各种媒体信息推送到距离移动终端较近的网络边缘,以减少核心网流量并提高对终端的服务质量[2-4]。

传统方法指出,终端可以关联到某方面最大化的基站,如最大接收信号强度、最大信干噪比、最大信道容量等。一种业界熟知的方案是蜂窝范围扩展(cell range expansion,CRE),扩大小蜂窝关联范围以提升网络容量或公平性[5]。文献[6]研究了一种基于能效的蜂窝关联算法,其优化目标为最大化能效,并可分布式地得到一个较优解。文献[7]提出了一种通过求解对数效用函数最优来获取关联策略的方法,通过松弛约束条件转化为凸优化问题并求解其拉格朗日对偶问题。还有一些研究通过组合优化来求解,如文献[8]通过求解基于二部图的匹配问题来获取蜂窝关联策略;文献[9]将蜂窝关联问题转化为二部图匹配问题,并采用贪婪算法求解。

然而这些方案在做蜂窝关联时均没有考虑终端接入基站后获取媒体信息内容所需的传输路径。未来5G网络边缘部署着高密度的小蜂窝,内容一般会在一些小蜂窝中存储,通过以上方案进行蜂窝关联会带来一个严重问题,即所关联蜂窝需要小蜂窝之间较长的路径来传输该内容。就业务实时性而言,传输时延是非常重要的因素,因此让内容获取路径尽量短是非常重要的。近年来关于内容获取的研究正在逐步展开,文献[10]根据流行度来实现内容分布式缓存,通过将流行的内容部署在终端附近,来减少服务器负载；文献[11]提出了一种基于Stackelberg博弈模型的边缘缓存方案来缓存视频；文献[12]提出了一种主动缓存机制,借助移动边缘计算架构的协同缓存学习策略与贪婪算法来解决内容部署问题。

为了使网络中的终端整体上均获得较好的服务质量,本文提出了一种联合优化内容获取路径与系统容量的蜂窝关联方案。首先利用贪婪算法求出内容在小蜂窝中的近似最优部署,再通过虚拟基站的方法将该问题转化为二部图的最优匹配,最后用匈牙利算法求得最优解。仿真结果表明,该方案可在多项式时间内得到一个对应效用函数最大化的蜂窝关联策略,并尽量减小内容获取路径的平均跳数。

1 系统模型

本文考虑有限地域范围内一个宏蜂窝和多个小蜂窝构成的5G异构网络,小蜂窝基站之间的媒体信息内容传输是通过光纤完成的。网络中有M个基站(包括宏基站和小基站),表示为{Ωi|i=1,…,M}。当前有内容请求的终端有N个,表示为{Uq|q=1,…,N},并简化假设每个终端仅有一个内容请求。

若Uq接入到Ωi,则Uq的上行信号与干扰加噪比(signal to interference plus noise ratio,SINR)表示为:

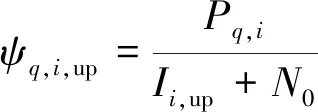
(1)

其中:Pq,i为Uq到Ωi的有效信号功率;N0为加性高斯白噪声;Ii,up为Ωi受到的来自接入周围基站的终端的上行平均干扰。因此,Uq获得的上行系统容量表示为:

(2)

其中:B为系统带宽;ni为接入Ωi的终端数量。ni表示为:

(3)

其中,bq,i为一个0/1整数变量,1表示Uq接入Ωi,0表示未接入。

Uq所获得的下行系统容量表示为:

(4)

其中,ψq,i,down为Uq接入Ωi的下行SINR,其计算方法与(1)式相同。

假设基站的存储有限,只能放入一个内容,且同一种内容部署在K个基站中。当Uq接入到Ωi后通过该基站获取内容的最小跳数为Si。在某时间段内,Ωi有ni个内容请求。若Ωi内有该内容,则Si为0,进而传输开销为0。否则,接入Ωi的每个终端收到该内容的平均传输开销为Siβ/ni,其中β表示单跳开销。(4)式除以ni的原因在于,该内容传至Ωi之后在某时间段内该内容仍存储在其缓存内,因此这ni个终端都可以直接从Ωi获取到该内容,而不需要将该内容从远端基站反复传至Ωi。当内容在网络中的部署已定时,蜂窝关联优化问题的目标函数可以表示为:

(5)

s.t.C1:bq,i∈{0,1},1≤i≤M;

其中:λ为上行业务占总传输业务的比率;ε用于表征系统容量和小蜂窝之间内容获取开销的权重,取值在0～1之间;C2确保了每个终端只能接入一个基站。效用函数取对数对应比例公平,它在实际问题上比直接优化效用函数应用更广泛[13]。

如果内容在网络中的部署未知,可以用一个0/1整数变量来表征内容在基站中的部署情况:

(6)

于是可以将内容部署建模为图的最短路径问题。由于不能给出一个简单的闭式解,需要用ai的函数来表示,即

Si=ming(ai)

(7)

于是问题(5)改为:

(8)

s.t.C1:ai∈{0,1}；

C2:bq,i∈{0,1},∀i∈Ω；

2 蜂窝关联的联合优化方案

因为(5)式和(8)式均涉及蜂窝关联和内容部署2个问题,导致直接求解比较复杂,所以需要将问题进行转化。

2.1 基于内容随机部署的联合优化方案

基于内容随机部署的方案是将内容部署在一些随机选定的基站中。由于内容是随机部署在基站中的,该方案的关键是优化终端的关联。

对于(5)式,可以将其转化为：

(9)

参照文献[7]的方法,通过将基站分解为虚拟基站,使终端与真实基站的关联转化为终端和虚拟基站的匹配。虚拟基站分解方法如图1所示。基站i用虚拟基站B(i)代替,因为有4个终端,所以B(i)由4个虚拟基站构成,图1a中与基站i相关联的终端2、3转化为分别与B(i)的前2个虚拟基站相连。

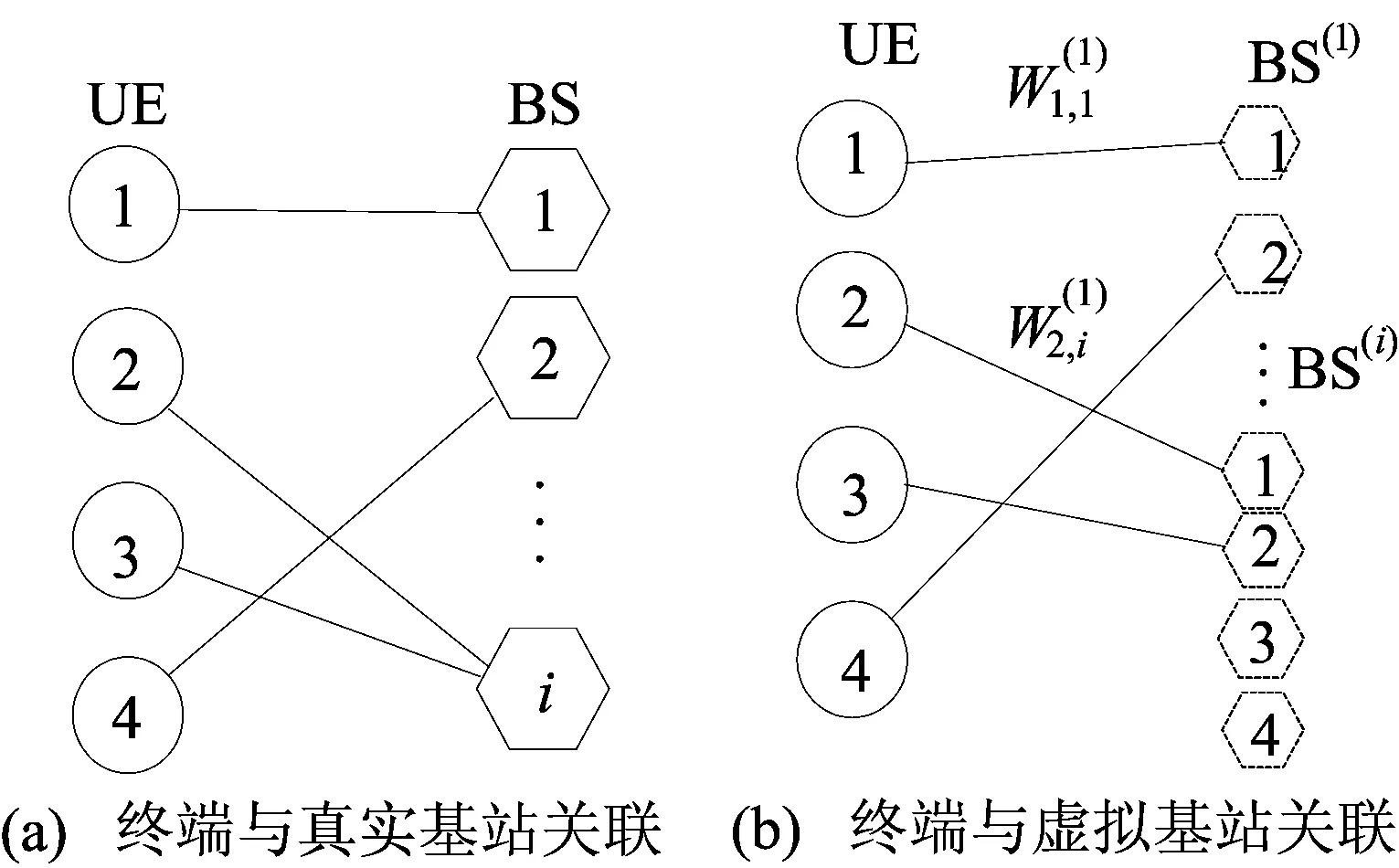
图1 虚拟基站分解方法

将终端与基站多对一关联下的权值求和转化为终端与虚拟基站的匹配权值之和,可以构造出终端和基站匹配的N×NM维虚拟权值矩阵,其元素可表示为:

(10)

其中,t为虚拟基站的序号。

因此(9)式等价于以下二部图匹配问题,可以利用匈牙利算法获得最优解。

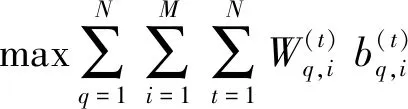
(11)

2.2 基于内容贪婪式部署的联合优化方案

上一节提出的基于内容随机部署的方案,因为内容随机部署会导致获取内容的平均跳数较大,所以需要设计更优的内容部署方案。对于(8)式,因为Si是不确定的值,不能直接以(5)式的方式进行转化,所以需要先给出一个近似最优的内容部署策略,即先利用某种算法求出一个近似最优的ai部署策略,然后在此基础上完成对(8)式的求解,具体求解方式与(5)式相同。

本文设计了一种基于贪婪式内容部署的蜂窝关联算法,流程图如图2所示。

具体算法步骤如下:

(1) 以基站为节点,由基站间连线形成一幅连通图,表示为G(V,E),其中V表示基站集合,E表示边的集合,E可以通过给定的阈值d-thd判断基站之间是否有连接得到,然后再利用Dijkstra算法计算出M×M维的基站间跳数矩阵H。

(2) 根据H和给定的内容部署数K,通过贪婪算法求出Si。

贪婪算法描述如下:①对于任一基站,求出其到其余基站的跳数总和,该步骤是对H每一列进行求和,选出到所有其他基站跳数之和最小的基站,将内容部署在该基站。当K=1时,这里求出的就已对应最优内容部署。②当K≥2时,需要将算法此前已经选出的内容部署基站到其他基站的跳数与任一基站到其他基站的跳数一一做差对比,并将较小的跳数值放入到对应的H里,更新H。这是因为当某一基站部署内容后,H需要根据该基站到其他基站的跳数和剩余基站到其他基站的跳数比较后更新,以作为下一次迭代的输入。③对步骤①、步骤②迭代K次,从而得到K个需要部署内容的基站。

3 性能仿真结果分析

仿真实验中,本文设置了1个宏蜂窝,若干个小蜂窝。其中宏蜂窝的半径为500 m,宏基站和小基站的传输功率分别置为46 dBm和21 dBm,终端的发射功率为30 dBm,带宽为1 MHz,信道路径损耗模型采用近距离自由空间路径损耗模型(close-in free space reference distance pathloss,CI-FSPL)[14],λ=0.5,ε=0.2,β=6×104。

3.1 单内容部署和蜂窝关联方案的性能对比

1个宏蜂窝、10个小蜂窝和100个终端,选择最大SINR[15]和基于匈牙利算法[9]这2种蜂窝关联方案与本文方案进行对比。最大SINR算法是求解蜂窝关联最经典的算法之一,而基于匈牙利算法的蜂窝关联算法可以求出最优系统容量。基于不同方案的蜂窝关联结果如图3所示。图3中：菱形表示部署的内容；绿色表示关联到宏蜂窝；黑色表示关联到小蜂窝。图3a中大多数终端均关联到宏蜂窝,是因为终端关联到宏蜂窝的SINR比较大。图3b～图3d中大多数终端会关联到小蜂窝,是因为基站的带宽有限,所以与最大SINR相比,大多数终端会关联到小蜂窝。图3c、图3d中终端关联到小蜂窝要多,是因为其还考虑了内容获取路径对蜂窝关联的影响。

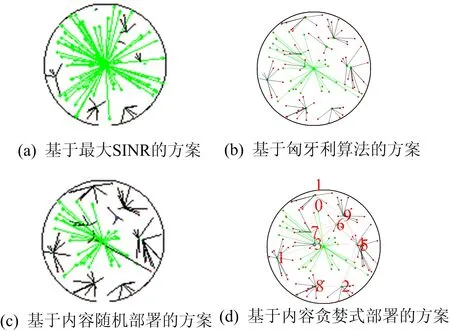
图3 不同方案的蜂窝关联结果对比

不同蜂窝关联方案的系统总效用对比如图4所示,从图4可以看出：随着部署内容的基站数量在增加；效用函数Zm的值在增加,且与其他算法相比,本文提出的基于内容贪婪式部署的方案的系统总效用最大。

不同蜂窝关联方案的平均跳数如图5所示。从图5可以看出,随着部署内容的基站数量增加,所有方案的平均跳数均逐渐减小,而本文方案明显优于最大SINR和基于匈牙利算法的方案,其中基于内容贪婪式部署的方案性能最好。以K=6为例,获取内容的平均跳数与基于匈牙利算法的方案相比降低了16.6 %,与最大SINR的方案相比降低了54.5%。基于不同蜂窝关联方案的终端系统容量总和如图6所示。从图6可以看出,最大SINR的终端系统容量最大。虽然本文提出的方案在系统容量方面与最大SINR方案相比有些差距,但与其他优化方案相比在系统容量方面没有降低。

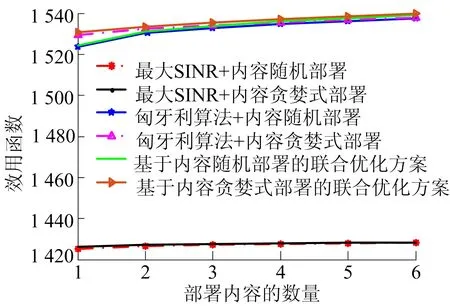
图4 不同方案的系统总效用对比

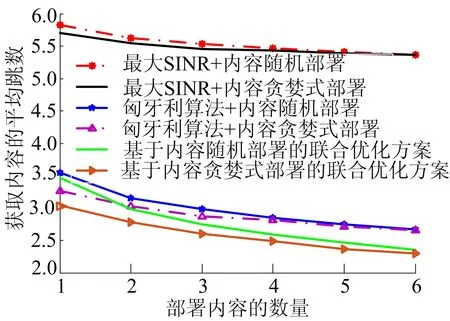
图5 不同方案的平均跳数

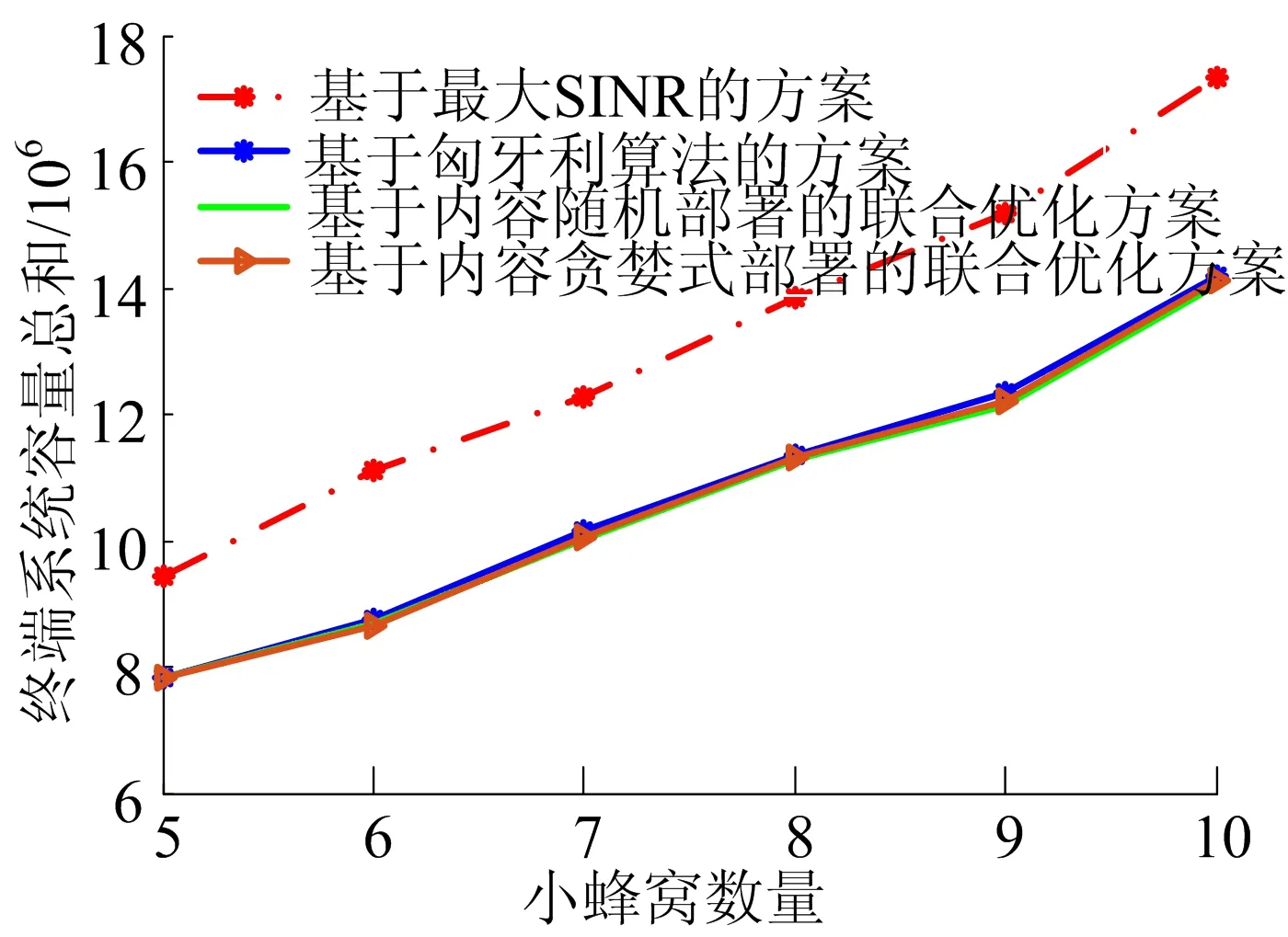
图6 基于不同蜂窝关联方案的终端系统容量总和

3.2 多内容部署和蜂窝关联方案的性能对比

假设网络中存在2种内容,且部署数量一样多。这2种内容也是根据贪婪算法进行内容部署的,不同之处在于先利用贪婪算法在一些基站中部署其中一种内容,然后在剩余的基站中再次利用贪婪算法部署另外一种内容。

对2种内容、1个宏蜂窝、10个小蜂窝和100个终端的情况进行仿真。基于不同方案的蜂窝关联结果如图7所示,图7中蓝色和红色的点分别表示部署了2种不同内容的基站。

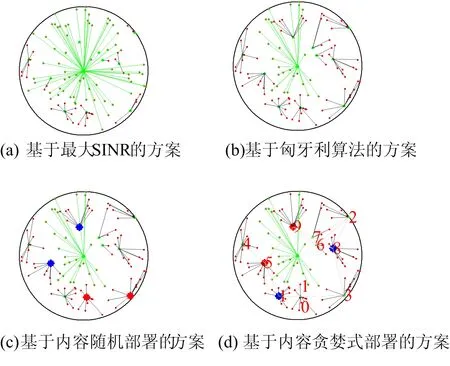
图7 不同方案的蜂窝关联结果对比

2种内容的不同蜂窝关联方案的系统总效用对比、不同蜂窝关联方案的平均跳数和不同蜂窝关联方案的终端系统容量总和如图8～图10所示,可以看出与部署单内容时的结果基本相同。

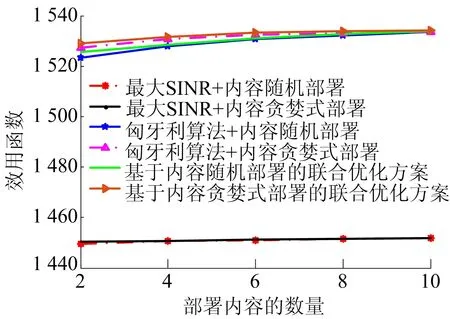
图8 不同方案的系统总效用对比

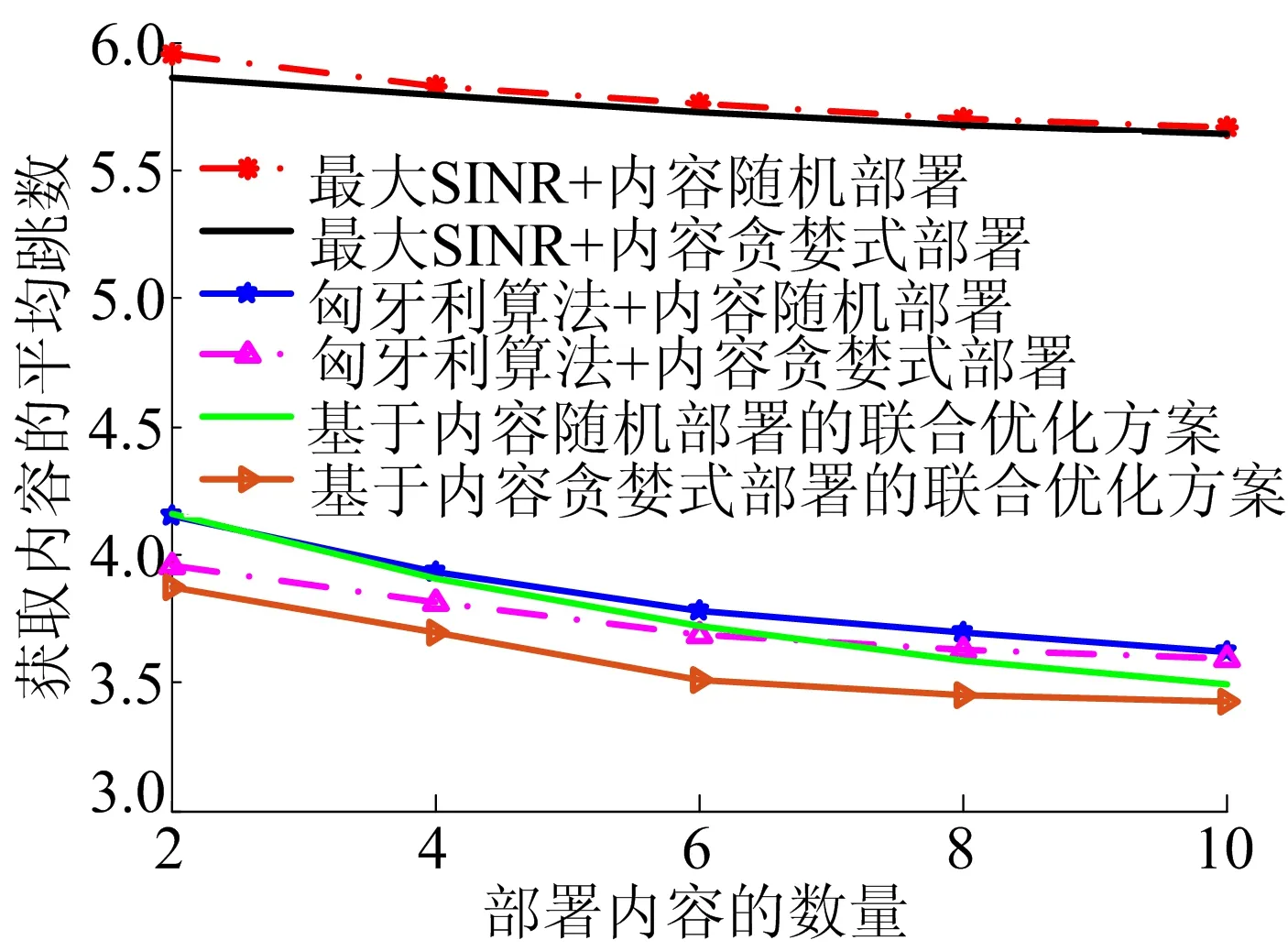
图9 不同方案的平均跳数

从图5和图9的比较可看出，当内容种类增多时,本文提出的方案平均跳数相对增加,其原因是基站的存储有限。

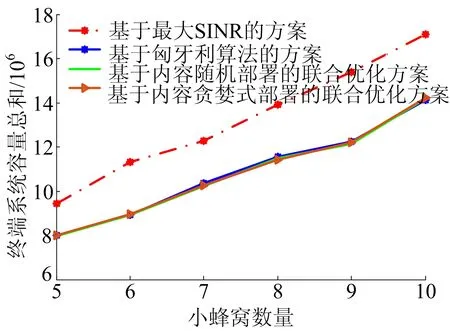
图10 基于不同蜂窝关联方案的终端系统容量总和

4 结 论

本文通过将内容获取路径和蜂窝关联联合考虑,提出一种联合优化内容获取路径与系统容量的蜂窝关联方案。该方案使用虚拟基站的方法,将效用函数最大化问题转化为基于二部图的最优匹配,并利用匈牙利算法求得最优解。通过仿真发现提出的方案比以往方案效用函数更大,且时延较小,即较传统方案而言更适合于高密度网络。由于未来网络中将部署大量的媒体信息内容,因此在以后的研究中需要将该方案扩展至基站存储更多内容的场景中去。