基于TRB结构的整车耐撞性可靠性优化

汪 伟, 赵 杰,王启栋,谷先广

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引 言

面对日益严峻的环境与能源危机,轻量化设计已经成为汽车行业的研究热点。然而,在实现减重的同时,必须要确保汽车的安全性能,如何兼顾轻量化设计和整车碰撞安全,已然成为科研工作人员所面临的重要工程应用问题[1-2]。目前,汽车轻量化设计的方法主要包括新材料、新结构和新工艺的应用[3-5]。高、超高强度钢以及碳纤维材料能够在很大程度上减轻重量,同时保证结构具有足够的强度,但由于成本过高不适合广泛应用。薄壁结构因其突出的变形吸能特性,受到了较多关注,但等厚度结构的轻量化潜力尚未充分挖掘出来。先进制造工艺下的激光拼焊板和连续变截面板(tailor rolled blank,TRB)结构能够很大程度地节省材料,已经在前纵梁、B柱等车身关键件上得到应用。研究表明,TRB相比于其他结构,具有低成本、材料利用率高、成型容易、力学性能优异等综合优势,在实现轻量化和提升结构耐撞性能方面具有很高的应用价值[6]。

近年来,大量学者对TRB结构的耐撞性能、吸能特性及工业应用进行了研究。其中,文献[7]综合利用实验与数值仿真方法对TRB帽型截面梁进行耐撞性分析,并研究其结构参数对吸能效果的影响。文献[8]将TRB应用于车身吸能盒,提高了结构的吸能效率和整车耐撞性能,但不足的是文中所构建的整车模型过于简化。文献[9]提出一种可变厚度的前纵梁结构,并对正面碰撞工况下的整车耐撞性能进行分析和优化。以上TRB结构在汽车上的应用,多局限于单个部件,而未能将TRB结构系统地应用于多个零部件。此外,对TRB结构参数的优化设计都基于确定性优化,没有考虑不确定因素对优化结果的影响,容易导致最优解超出约束边界而失效。因此,可靠性优化设计(reliability optimization design, ROD)在TRB结构的优化过程中意义重大。

综上所述,本文将一种新型结构TRB应用于汽车保险杠、吸能盒和前纵梁,并参考中国新车评价规程(China new car assessment program, C-NCAP),系统地将试验设计、代理模型技术、多目标优化理论及可靠性优化方法应用于整车耐撞性的优化设计中,提高汽车安全性能,实现轻量化,同时保证优化设计结果的可靠性。

1 优化设计方法与准则

1.1 可靠性优化方法

可靠性优化ROD通常指在可靠性约束条件的基础上对产品进行优化设计。因此,在可靠性优化之前,需要进行确定性优化。典型的确定性优化数学模型可以表示为:

(1)

其中:M、N分别为目标函数f(x)、约束函数g(x)的数量;xU、xL为设计变量的上、下限。

对于确定性优化,当设计变量由于加工误差等外界因素发生扰动时,目标函数值可能因设计变量的波动而发生较大变动,以致优化方案不满足约束条件而失效。通常,需要对确定性优化结果进行可靠性分析,评估其可靠度是否能满足工程需求。若可靠度不满足要求,则需进一步开展可靠性优化。

可靠性优化的数学模型[10]为:

(2)

其中:μ为优化目标均值;P[gi(x)≤0]为满足第i个约束的概率;Ri为约束函数gi(x)的可靠度需求。

在ROD可靠性优化设计中,失效概率可表示为:

(3)

其中:Pi为第i个约束条件的失效概率;fxx为联合概率密度函数。

1.2 多目标粒子群算法

粒子群优化(particle swarm optimization, PSO)算法的概念最早源于鸟类的捕食行为,由Eberhart和Kennedy于1995年提出,其后进行了一定的改进。其基本思路为:在假定的D维搜索空间内,有m个粒子组成的种群,每个粒子在搜索空间中的位置和速度分别用D维向量xi=[xi1xi2…xiD]和vi=[vi1vi2…viD]表示,其中i=1,2,…,m。每一次迭代中,根据个体极值xPbest和种群极值xGbest,粒子按照迭代公式不断迭代更新自己的速度及位置,直至达到定义的终止标准[11]。迭代公式为：

(4)

(5)

其中:c1、c2为加速系数;r1、r2为介于[0,1]之间的随机数;ω为惯性权重系数。

典型的PSO算法参数见表1所列。

多目标粒子群优化(multi-objective particle swarm optimization,MPSO)算法作为粒子群优化算法的扩展,因其能够快速收敛到一个合理可接受的解而被广泛应用于解决多目标工程应用问题[12]。为此,本文引入MPSO算法,对车辆的耐撞性和轻量化多目标问题进行确定性优化和可靠性的优化设计。

表1 典型PSO算法参数

1.3 汽车正面碰撞耐撞性设计准则

汽车正面碰撞最为常见,因而对正面碰撞工况下整车的安全性能研究显得尤为重要。典型的正面100%碰撞工况及碰撞空间管理如图1a所示。在耐撞性设计中,前端结构有效的变形和吸能,可以很大程度上减小碰撞加速度及防火墙的侵入量,提高整车的耐撞性能。当正面碰撞发生时,车辆前端结构通常表现为轴向压溃和弯曲的混合变形模式来抵抗冲击载荷。由于弯曲导致的能量吸收比轴向压缩要少得多,在设计过程中应尽量引导结构发生轴向压溃变形。图1a中的区域A应产生相对均匀的渐进式压溃模式,以实现稳定变形和能量吸收。

为了系统地评价结构耐撞性能,本文给出了常用的性能指标,即吸能值(energy absorption)、平均碰撞力(mean crushing force)、比吸能(specific energy absorption)。

吸能值表示压溃变形过程中结构吸收的总能量,即

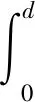
(6)

平均碰撞力为结构吸收冲击能量的能力,可以表示为:

(7)

比吸能描述为单位质量结构的吸能效果,数学表达式为:

(8)

其中:d为压缩距离;F(x)为瞬时冲击力随压缩距离变化的函数;M为吸能结构的总质量。

碰撞加速度波形作为评价整车耐撞性的重要指标之一,对乘员保护具有重要意义。为更加直观地描述加速度曲线,本文引入二阶波形模型,如图1b所示。其中,第1阶段加速度G1代表吸能盒和前纵梁前端结构的压溃吸能过程;第2阶段加速度G2表示发动机末端与防火墙开始接触,进而入侵乘员舱的过程。通常,为获得较高的整车耐撞性能,要求提高一阶加速度并减小二阶加速度[13]。因此,在前端结构设计的过程中,区域A应当能够高效地吸能,区域B不能被过量压缩,以保证乘员舱的完整。

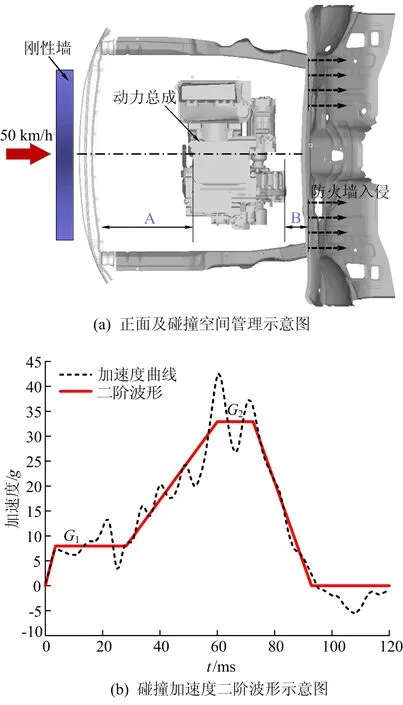
图1 正面碰撞设计原理示意图

2 有限元模型建立与验证

2.1 整车有限元模型验证

为分析某轿车的整车耐撞性能,本文基于正面100%重叠刚性壁障碰撞试验程序,按照C-NCAP法规,模拟整车以50 km/h的速度与刚性墙发生碰撞。整车有限元模型包含601 363个节点,957 824个单元,近90%的单元为壳单元且单元大小为10 mm, 整车总质量为1 275 kg。在仿真分析及优化设计之前,需要对有限元仿真模型的精度进行验证。碰撞前、后实车试验和有限元仿真对比的结果如图2所示。由图2a可知,试验与仿真过程中车辆碰撞变形的模式保持一致;由图2b可知，试验与仿真的碰撞加速度随时间的变化趋势基本一致，加速度峰值也十分接近。由此说明,本文建立的整车碰撞有限元模型具有较高的精度,可用于后续的优化设计。

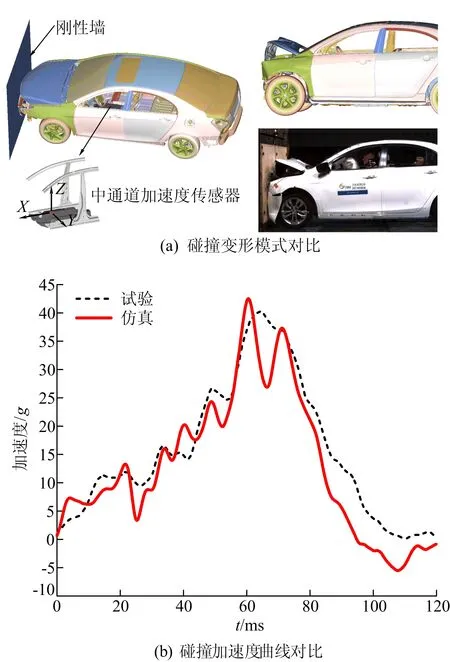
图2 整车正面碰撞试验与有限元仿真对比

2.2 前端结构TRB有限元模型建立

考虑到TRB结构的制造工艺和成型特性,其有限元模型的建立与等厚度结构有限元模型构建方式存在着一定的差异,主要表现在材料厚度和材料属性2个方面。由于不同厚度结构的材料属性有所差异,在建立TRB仿真模型之前,需要建立准确的材料模型。

本文应用的材料为高强度钢HSLA340，其密度为7.8×103kg/m3，杨氏模量为210 GPa，泊松比为0.33。在结构发生大变形时,高强度钢通常表现出典型的应变率依赖性,因此需要考虑材料的应变率效应,其本构模型Cowper-Symonds可表示为:

(9)

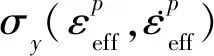
TRB结构的连续变厚度特性将导致其材料呈现非均一性,而正常的单一材料属性不足以精确地表达TRB变厚度区材料特性。为解决这一问题,利用二阶Lagrange多项式插值法对几组不同厚度的材料应力应变曲线[9]进行插值,以获取任意厚度的材料应力应变关系。 不同厚度的材料应力应变曲线如图3所示。

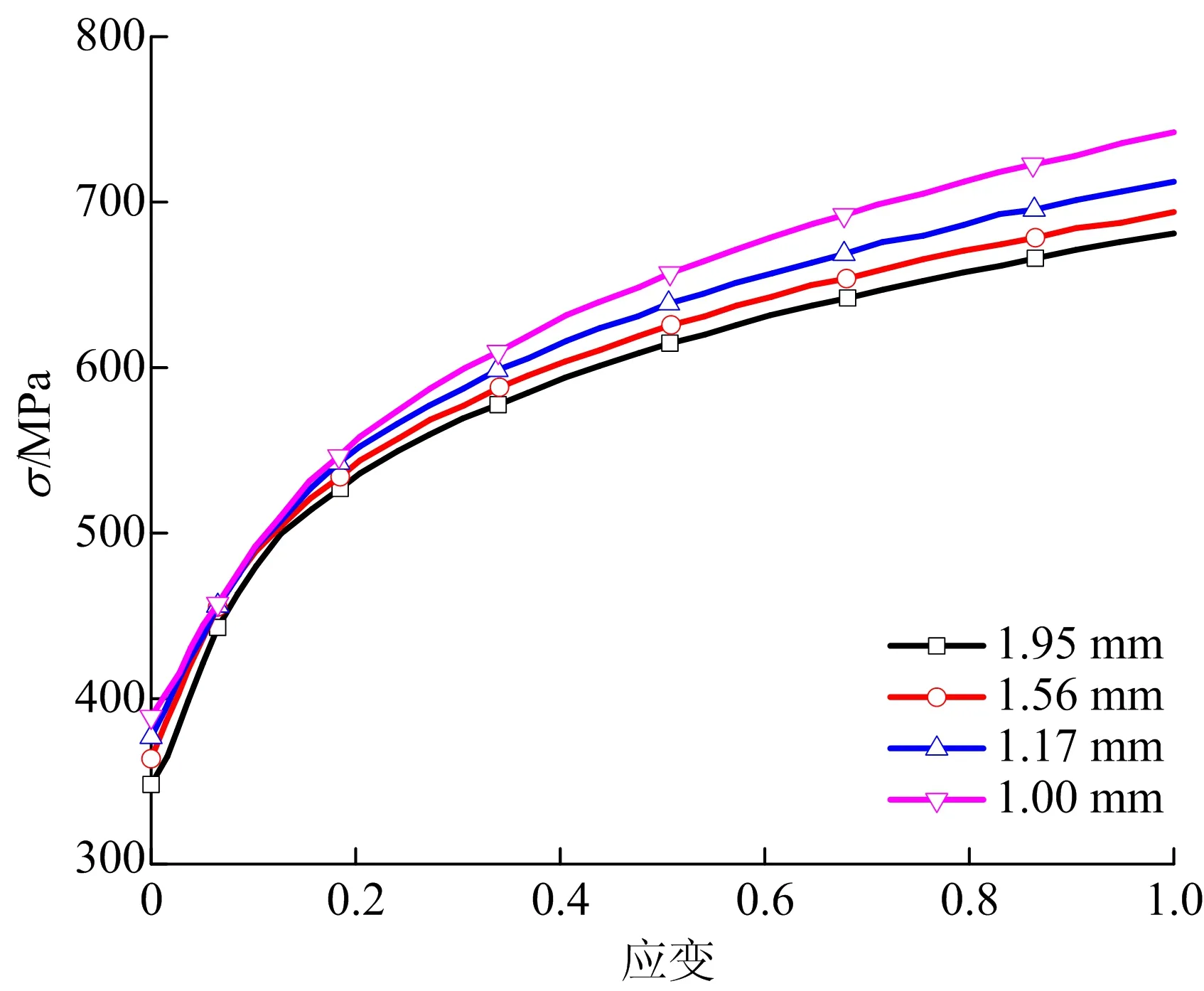
图3 不同厚度的材料应力应变曲线

在轴向的压溃变形过程中,构件厚度从前端至后端呈逐渐递增的趋势,将对结构压溃变形模式和能量吸收有着重要作用,这不仅有助于降低峰值冲击载荷,而且还有助于提高整体变形的稳定性。

本文对TRB结构吸能盒和前纵梁的设计也是基于这一原则。而对于TRB结构的保险杆横梁,更多的材料应当集中于中心碰撞区域,以获得足够的刚度和更高的吸能效率。

汽车前端关键吸能件的TRB结构几何示意如图4a所示。整体TRB几何由等厚度区域(constant thickness zone, CTZ)和厚度过渡区域(thickness transition zone, TTZ)组成。等厚度区域的材料属性一致,而变厚度区域需要被离散为多个独立的部分,以赋予不同的材料属性。考虑到TRB结构的制造成本,变厚度过渡区域的斜率应控制为1∶100[14]。碰撞空间约束条件的限制,前纵梁主要压缩吸能区域L设为225 mm,其他厚度及位置尺寸(x1～x9)将作为后续优化过程中的设计变量。

TRB结构的有限元建模可以在非线性软件LS-DYNA中完成。利用4节点B-T变厚度单元来模拟TRB结构的实际厚度变化,其关键字为*ELMENT-SHELL-THICKNESS,单元大小设为3 mm以保证模型的仿真精度。材料模型HSLA340定义为分段线弹塑性材料(Mat24),不同厚度的单元被赋予不同的材料属性。保险杆横梁的TRB有限元模型如图4b所示。

模型中的常用接触算法为自接触和面对面接触,其中静态摩擦系数和动态摩擦系数分别设为0.35、0.25[7]。

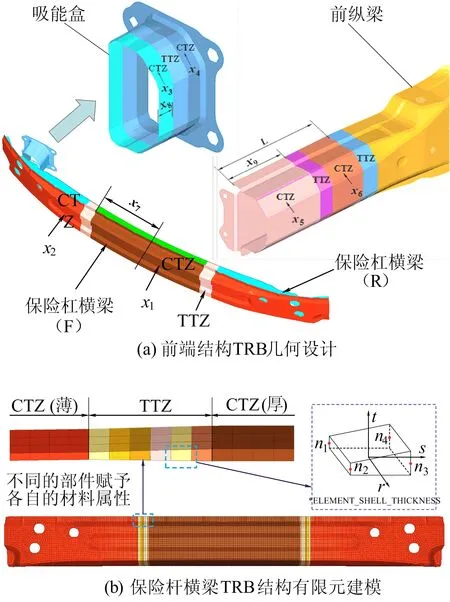
图4 前端结构TRB有限元模型示意图

3 优化设计

优化设计的流程如图5所示,主要包括有限元模型的建立和验证、优化问题定义、试验设计、代理模型建立、确定性优化设计、可靠性优化设计和优化结果验证。

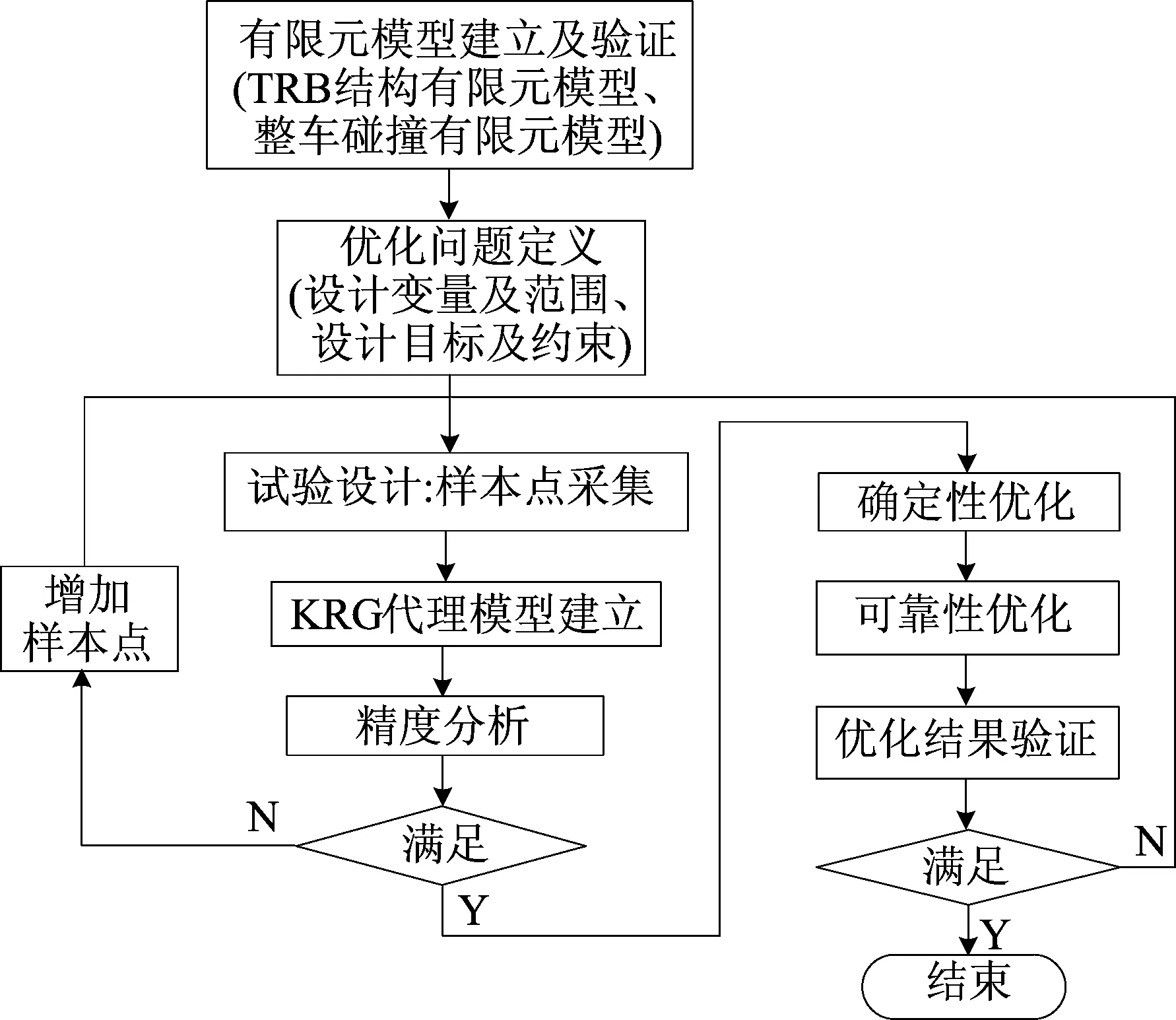
图5 优化设计流程

3.1 多目标优化问题定义

汽车前端结构的优化设计主要目的在于提高整车的耐撞性和减轻质量。因此,以关键吸能件的总吸能E(x)和质量M(x)作为设计目标；以耐撞性指标，即碰撞峰值加速度A(x)、第1阶段加速度G1(x)、第2阶段加速度G2(x)以及防火墙入侵量I(x)作为设计约束。

各响应的初始设计值及优化设计目标见表2所列。研究和工程经验表明,TRB的结构参数对其耐撞性和吸能效果有着很大的影响,因此本文选取关键吸能件TRB结构的厚度参数(x1～x6)和位置参数(x7～x9)作为设计变量。同时,考虑到TRB结构制造工艺等不确定性因素的影响,可靠性设计中假定设计变量服从正态分布,协方差系数(σ/μ)设为0.03。

设计变量的初始值、变化范围及概率分布见表3所列。

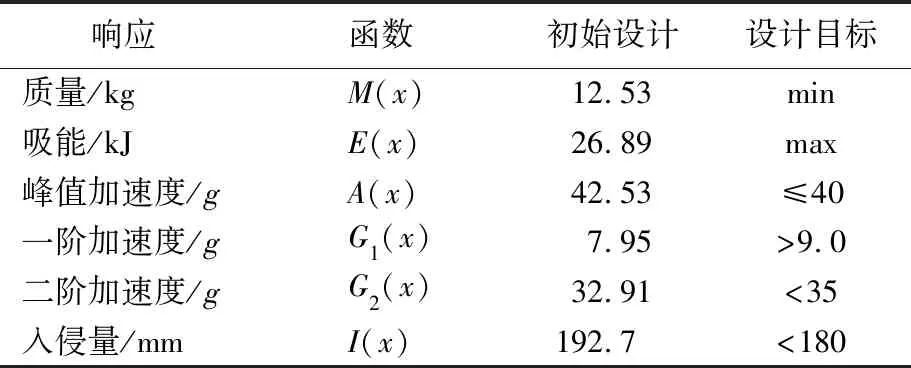
表2 响应的初始设计及设计目标

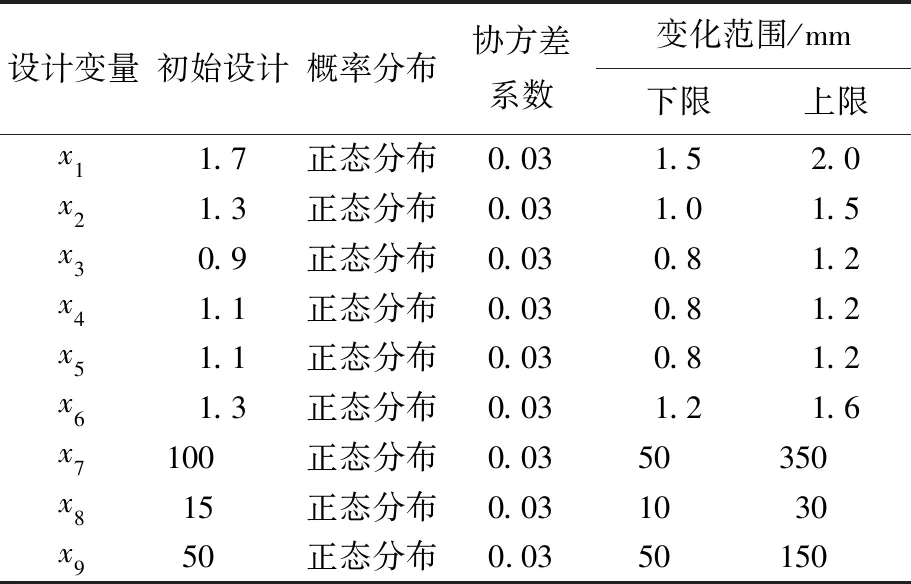
表3 变量的初始设计及概率分布

3.2 试验设计与代理模型构建

试验设计与代理模型相结合的数学预测方法,能够有效地降低计算成本,提高优化效率,已被广泛地应用于汽车工程研究领域。本文利用最优拉丁超立方(optimal Latin hypercube sampling, OLHS)试验设计,在有限的设计空间内生成60组样本点,以保证样本点具有很好的填充性和均匀性。再利用有限元分析软件计算各样本点处的响应值,完成样本数据的构建。克里金KRG代理模型在构建多参数、多响应等复杂非线性问题的函数关系时已经被证明具有较高的拟合精度[15]。本文基于试验设计样本数据,采用KRG模型构建设计变量与响应之间的数学模型用于后续的优化设计工作。为验证代理模型的精度,还需要另外生成20组样本数据。常用的代理模型精度评估参数有确定性系数(coefficient of determination)、均方根误差(root mean square error),其表达式为:

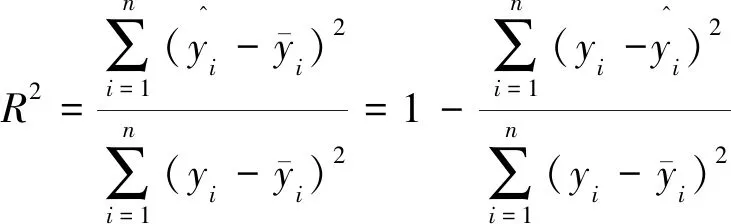
(10)

(11)

其中:R2为确定性系数；ERMS为均方根误差；yi为实际的响应值;R2为预测响应值。

KRG代理模型的精度验证指标见表4所列,所有响应的确定性系数R2都大于0.9且均方根误差ERMS值都小于0.1,达到了近似模型的精度要求,可用于后续优化。

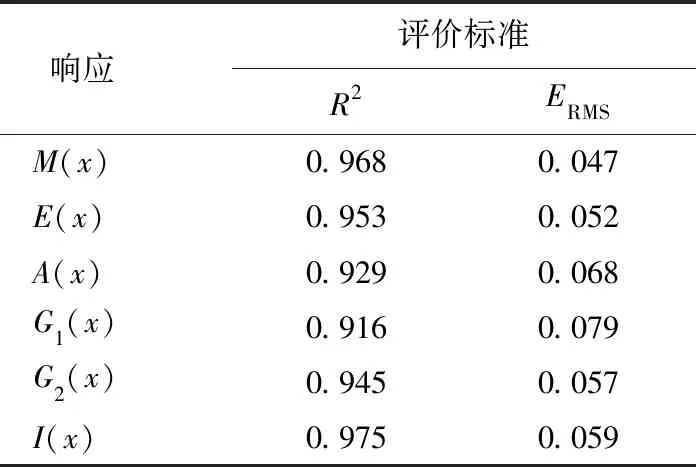
表4 确定性和可靠性优化设计结果对比

3.3 优化过程及结果对比

确定性优化和ROD优化设计的数学模型表达式分别如下:

min {M(x),-E(x)};

s.t.A(x)≤40g,

G1(x)≥8g,

G2(x)≤35g,

I(x)≤180 mm,

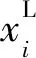
(12)

minμ{M(x),-E(x)};

s.t.P(A1(x)≤40g)≥95%,

P(A2(x)≤40g)≥95%,

P(I(x)≤185 mm)≥95%,

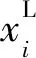
(13)

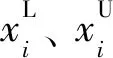
实际上,整车耐撞性和轻量化设计问题的求解是个多目标优化过程。MPSO由于其低计算成本和高求解质量而被广泛应用,本文以MPSO为求解器,来寻求设计变量的最优参数分布。蒙特卡罗抽样估计(Monte Carto sampling, MCS)是一种常用的准确评估概率特性的方法,在ROD优化设计的过程中,基于MCS方法进行1 000次抽样,并用蒙特卡罗算法估计约束条件的可靠度。确定性和可靠性的优化结果及可靠度对比见表5所列。对比确定性优化,可靠性优化后的约束条件可靠度有着显著提高;此外,虽然可靠性优化结果在设计目标质量M(x)和总吸能E(x)上有所损失,但耐撞性指标峰值加速度A(x)和防火墙入侵量I(x)得到了改善。综上可知,ROD优化设计的结果优于确定性优化设计的解,因此选择ROD优化设计的最优解作为最终优化方案。

表5 确定性和可靠性优化设计结果对比

3.4 优化结果验证及分析

优化设计方案的变量取值见表6所列。考虑到优化结果来自于代理模型的预测,因此需要对优化设计方案进行可行性验证。

将优化设计变量值代入有限元模型进行仿真计算,获取响应值,并与模型预测值进行对比分析,结果见表7所列。从表7可以看出,模型预测响应值和有限元模型仿真结果的相对误差均小于5%,因此可以证明本文构建的代理模型具有较高的拟合精度。

由初始设计和优化设计的结果对比可知,相比于初始设计,优化后的质量减少12.8%,峰值加速度、第1阶段加速度、第2阶段加速度分别降低了9.78%、-17.8%、4.45%,防火墙侵入量减小了15.9%。同时,由(6)式～(8)式可以计算结构的3个常见吸能指标，其中优化后的EA、FMC均增加8.78%,ESA增加28.3%,表明了吸能效率的提升。

表6 初始和优化设计变量对比 mm

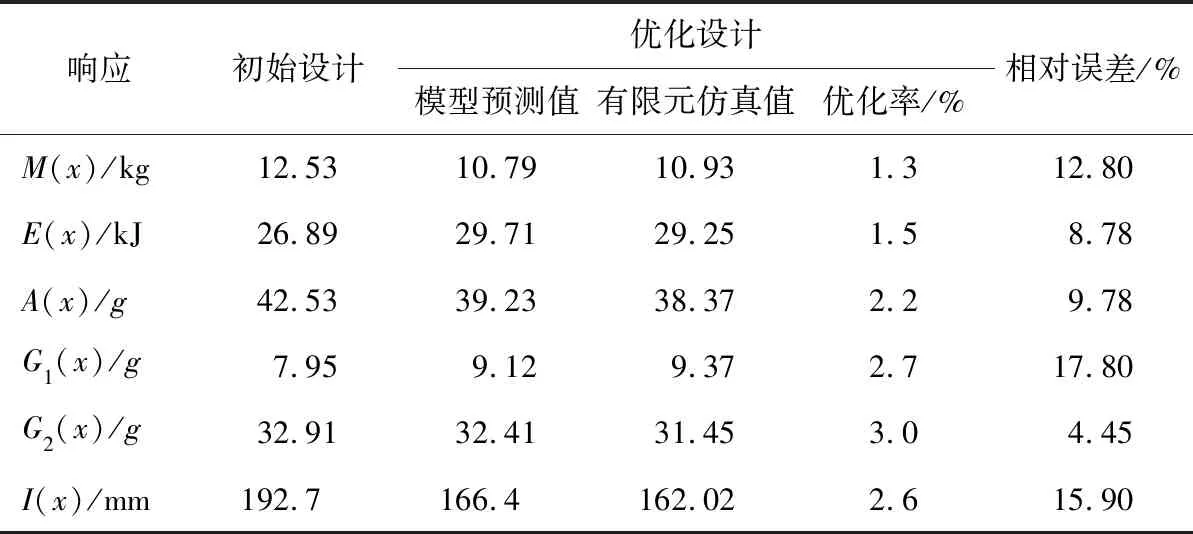
表7 初始和优化设计结果对比

优化前、后整车耐撞性指标的对比结果如图6所示。

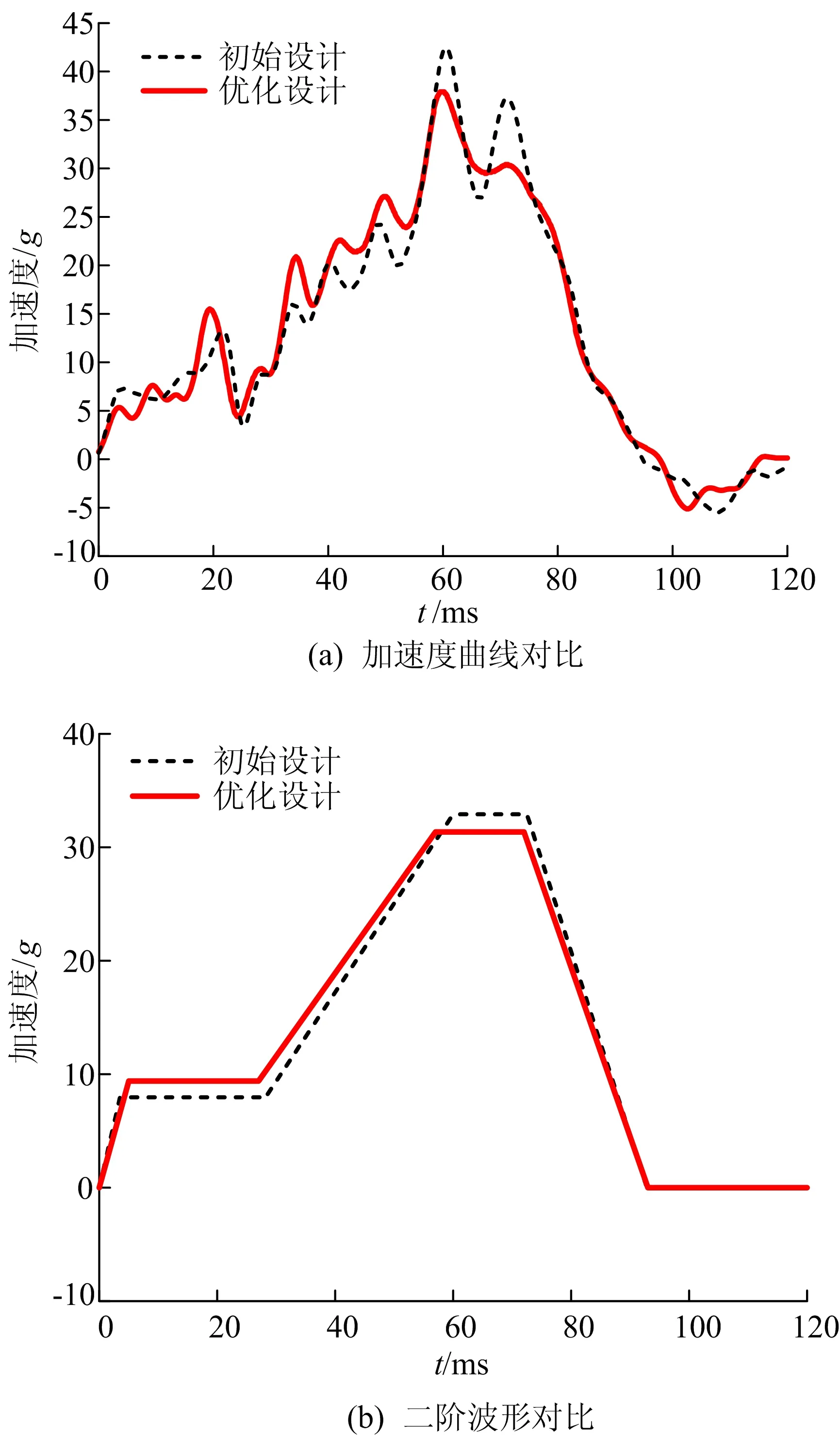
图6 优化设计与初始设计结果对比

由图6a和图6b可知,优化设计方案降低了峰值加速度和二阶加速度值,同时一阶加速度值有一定的上升,意味着碰撞加速度波形得到了较大程度的改善,这将对乘员保护起到重要作用。由吸能件总的能量吸收曲线对比结果(图6c)可知,尽管碰撞初始阶段优化的TRB结构吸收能量较少,但随着压缩距离的增大,总能量吸收值比初始设计更大,提高了结构的变形吸能效率。由优化前、后驾驶员侧防火墙入侵量的对比(图6d)可知,相比于初始设计的193 mm, 优化方案的动态入侵量降低至162 mm,乘员舱的安全性进一步提升。

4 结 论

(1) 本文建立并验证了整车碰撞有限元模型的有效性,并将TRB结构应用于汽车前端关键吸能件,结合数值仿真,对整车耐撞性能进行分析。

(2) 将ROD优化设计应用于TRB结构参数的优化。确定性优化和可靠性优化的对比结果表明,可靠性优化方案相比于确定性优化尽管在质量和吸能上有所损失,但各项耐撞性指标的可靠度明显提高,并确定其为最终的优化方案。

(3) 优化结果表明,优化的TRB前端结构总质量减轻12.8%,吸能增加8.78%,比吸能增加28.3%,碰撞峰值加速度、一阶加速度、二阶加速度分别降低了9.78%、-17.8%、4.45%,防火墙侵入量减小了15.9%。在实现轻量化的同时,整车的耐撞性能得到了显著提升。