铁路简支箱梁扭转变形性能分析
李清池 胡所亭 石龙 苏永华
(中国铁道科学研究院集团有限公司,北京 100081)
混凝土简支箱梁凭借其良好的空间整体受力性能,在工程上得到了广泛应用,然而在偏载荷载作用下箱梁不仅会产生弯曲变形,同时将发生刚性扭转和畸变[1]。工程实践与理论分析表明,畸变与扭转对薄壁箱梁的不利影响不可忽视[2]。近些年国内外对箱梁桥扭转畸变进行了大量的理论和试验研究[3],但多以公路箱梁为主,铁路箱梁较少,且从变形性能角度研究得较少。抗扭研究更多倾向于扭转参数的计算设计及梁体维护方面[4-7],将理论解析、有限元模型求解、工程试验三者结合起来的研究较少。为了满足大跨度的要求、配合高强轻质材料选用和适应预应力技术的快速发展,箱梁的截面变得更薄更宽[8],扭转畸变效应会扩大。因此,需要对铁路箱梁变形性能予以研究。
本文针对铁路设计速度250 km/h 的简支箱梁进行研究,辅以速度为350 km/h 箱梁、印度雅万高速铁路箱梁数据,利用杆系单元、实体单元建模计算偏载时最大扭转角差异,与偏载试验数据进行对比。利用材料力学公式计算法[9]、乌曼斯基第二理论法[10]分析这两种模型的变形差异。
1 概述
速度250 km/h 的铁路简支箱梁采用C50 混凝土,长32.6 m,计算跨度为31.5 m,梁高2.6 m,上顶板宽12.2 m,下底板宽5.3 m。简支箱梁横截面见图1。

图1 速度为250 km/h的铁路简支梁横截面(单位:mm)
考虑2种不同荷载工况:单线ZK 活载加载和十点偏载加载。根据TB/T 3466—2016《铁路列车荷载图式》[11],ZK活载的加载方式见图2,动力系数取1.0861。根据设计图纸,单线ZK 活载横桥向偏离梁体中心线2.3 m。
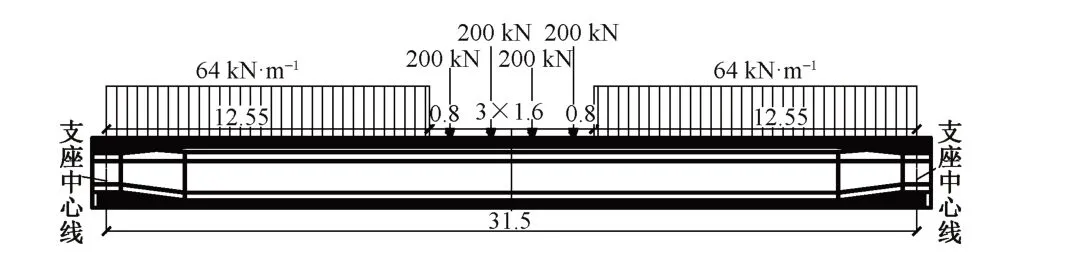
图2 单线ZK活载纵向布置(单位:m)
简支箱梁的质量检验可通过静载试验完成[12],设计十点偏载工况等效模拟单线ZK 活载工况。利用杆系单元模拟梁体受单线ZK 活载工况,设计十点偏载荷载值使其扭转变形相同。偏载侧单顶荷载为805.9 kN,对应侧单顶荷载481.7 kN。参考TB/T 2092—2018《简支梁试验方法预应力混凝土梁静载弯曲试验》[13],偏载试验采用分级加载的方式,加载图式见图3。

图3 偏载荷载布置(单位:m)
2 杆系单元与实体单元建模求解
2.1 杆系单元建模求解
杆系单元采用梁单元。在施加偏载时,在梁单元线上添加横向的弹性约束,以弯矩的形式施加荷载。梁端的约束形式采用单支座铰接形式。
杆系单元计算的扭转角分布见图4。可见,最大扭转角均为0.1010‰,单线ZK 活载和十点偏载在杆系单元模拟中梁的最大扭转角一致。

图4 杆系单元计算的扭转角分布
2.2 实体单元建模求解
实体单元建模中采用自动六面体网格划分,划分单元尺寸为0.1 m。两端约束情况与约束扭转解析法一致:梁端转角θ= 0,约束扭转双力矩βl= 0,在4 个支座处布置铰接约束,截面顶板施加横向约束。实体单元建模示意见图5。

图5 实体单元建模示意
计算得到的实体单元扭转角见图6。可见,单线ZK 活载、十点偏载下最大扭转角分别为0.3449‰,0.2606‰,差距较大。

图6 实体单元计算扭转角分布
3 试验验证
为了证实杆系单元和实体单元何种更趋于实际,设计试验对模型进行验证,对速度为350 km/h 的简支箱梁和印度雅万高速铁路简支箱梁做同样求解与试验,以增加数据可靠性。偏载试验的设计方法同第1节中介绍,每片梁设计4 次偏载试验。实体单元的约束情况与实际一致,为4 个支座约束。试验方法同TB/T 2092—2018。在梁的跨中截面、两端支座中心线截面处的左右各布置1 个百分表,共3 个截面,6 个百分表测点,测试梁体在试验荷载作用下的变形情况。跨中最大扭转角的计算方法是将两侧跨中竖向位移分别减去对应侧的支座位移平均值,以消除支座沉降因素,得到跨中两侧的竖向位移z1,z2,跨中测点的横向距离为Δy,则扭转角φ为

十点偏载工况下不同计算方法和试验扭转角计算结果见表1。

表1 十点偏载工况下不同计算方法的扭转角 ‰
由表1 可见,在偏载工况下实体单元能更好地反映实际情况,而杆系单元则差距较大,为实际情况的30% ~50%。因此,利用杆系单元计算设计偏载试验是不合理的,应该采用实体单元建模设计偏载试验来模拟单线ZK活载加载情况。
4 解析分析讨论
针对铁路箱梁杆系单元和实体单元模型在偏载荷载下的变形差异,利用材料力学公式计算法、乌曼斯基第二理论法进行解析解的分析与讨论。
4.1 材料力学公式法求解
假设该梁在扭转中满足平截面假设,根据材料力学公式

式中:dφ/dx为扭转角沿梁长方向的变化情况;T为截面所受扭矩;G为材料的剪切模量;Iρ为极惯性矩。

式中:ρ为截面上点到形心轴的距离;A为截面面积。
积分得到该梁的跨中截面Iρ中= 16.855 m4,梁端截面Iρ端= 24.403 m4。材料力学公式计算得到的扭转角分布见图7。可见,活载下扭转角最大为0.0977‰,偏载下扭转角最大为0.0979‰,与杆系单元计算结果仅差3%。

图7 材料力学公式计算得到的扭转角分布
4.2 乌曼斯基第二理论法求解
扭转理论的解析方法主要由符拉索夫和乌曼斯基建立,乌曼斯基第二理论是扭转解析法的基础。设直线坐标系中z为梁轴方向,s为扇形坐标用于确定截面上各点的位置,则u(z,s)为梁上各点的纵向位移,θ′(z)表示扭率,扭率仅与截面的位置有关。有约束的扭转翘曲位移计算式为

式中:u0(z,0)为截面z扇形左边为0 处的翘曲位移;β′(z)为待求函数;ωˉ(s)为广义扇形坐标,反映了截面的几何特征,计算式为

式中:h为截面顶板、底板、腹板中心线到广义扇形坐标中心的距离;Ω 为箱梁薄壁中线所围面积的2 倍;t为顶板、底板、腹板对应的板厚。
将箱梁截面进行简化得出主扇形坐标图,见图8。

图8 截面主扇形坐标(单位:m2)
对式(4)进行求解,主要依据两个条件:①沿箱梁周边一周始点与终点的u相等;②内外力矩平衡。可得

式中:E为弹性模量;θ(z)为截面扭转角;mt= dMk/dz为弯矩沿梁长变化程度;Id=为截面自由扭转惯性矩;Iωˉ=为扇形惯性矩;μ= 1-Id/Iρ为截面的约束系数,反映了截面受约束的程度。
可求得跨中截面约束系数μ中= 0.3986,梁端截面μ端= 0.4599。
对式(6)和式(7)进行求解,θ(z)的通解为

式中:C1,C2,C3,C4为θ(z)通解中的待定系数;k2=μGId/EIωˉ。
带入铰端约束条件θ= 0,βl= 0(βl= -EIωˉβ″(z)为约束扭转双力矩)。可得约束扭转下扭转角分布,见图9。可见,最大扭转角分别为0.2771‰,0.3570‰,与实体单元计算值差5%。

图9 约束扭转下扭转角分布
乌曼斯基第二理论的翘曲正应力σω计算式[14]为

截面上约束扭转正应力的分布和扇形坐标成正比。带入数据,可得速度为250 km/h 铁路简支箱梁跨中截面的扭转正应力分布,见图10。

图10 速度为250 km/h 简支箱梁跨中截面扭转正应力分布(单位:MPa)
由图10 可见,单线ZK 活载荷载下底板底缘的最大扭转正应为σω= 0.3866 MPa。在施加单线ZK活载时,求解其跨中下缘弯曲正应力为σ= 2.5492 MPa,二者比值为0.1517,符合常用对称预应力混凝土箱梁截面中由偏载产生的约束扭转正应力占活载弯曲正应力的15%左右[10]。
4.3 对比分析
将3类梁型的解析解与三维有限元的最大扭转角进行对比,见表2。

表2 3类梁型解析解与三维有限元的最大扭转角对比
由表2可见:
1)对比材料力学公式法与杆系单元的计算结果可知,在误差允许范围内软件在处理杆系单元的偏载工况时可采用式(2)进行求解,且视形心位置为扭转中心位置。
2)由约束扭转解析法与三维实体单元建模计算结果对比可知,利用乌曼斯基第二理论的约束扭转解析解可以大致模拟实体单元在偏载荷载下简支梁体的扭转变形情况。
3)同一种梁、同一种荷载工况下杆系单元和实体单元的计算结果差距明显。
4)同一种梁在十点偏载和单线ZK 活载加载时,杆系单元二者的扭转变形结果趋于一致,实体单元二者却有明显差距。
5 结论
本文通过对铁路简支梁在两种加载工况下分别采用杆系单元和实体单元建模求解其变形情况,与试验数据对比,通过理论解析法分析变形差异,得到以下结论:
1)利用实体单元建模能最接近地模拟简支箱梁实际的受扭变形,而杆系单元的求解值仅为实际的30%~50%。
2)采用杆系单元建模,两种加载工况下梁的扭转变形相近,但采用实体单元建模则可能相差较大,差值大小与梁型有关。设计偏载试验检验梁的抗扭刚度时,应采用实体单元建模分析。
3)实体单元和杆系单元在抗扭刚度上的不同,主要与实体单元的翘曲正应力有关,验证了常用对预应力混凝土箱梁截面中,由偏载产生的约束扭转正应力占活载弯曲正应力的15%左右。

