高海拔地区钢-混凝土组合梁日照温度场研究

陈胜利 苏永华 班新林 石龙

（1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.高速铁路轨道技术国家重点实验室，北京 100081）

桥梁结构在日照作用下会产生非线性的温度分布［1]，温度应力和变形有时会超过荷载所产生的效应，从而造成桥梁的损伤与破坏。钢-混凝土组合梁中钢材的导热系数约为混凝土的10倍，两种材料导热性能的巨大差异使得钢梁和混凝土桥面板之间存在很大的竖向温度梯度。

目前国内外学者对此进行了研究，孙国晨等［2]应用Ansys 有限元软件对钢-混凝土组合梁在日照作用下的温度场进行时程仿真分析，计算结果与实测数据吻合很好，验证了计算方法的准确性；武庆祥等［3]通过北京地区某钢-混组合箱梁日照温度场的分析，探究了组合梁桥的竖向、横向温度曲线的时程变化规律，并与现行规范进行了对比；季德钧等［4]以青海黄南地区哇加滩黄河大桥为背景，指出在青海高原高寒地区，采用考虑地理位置修正的主梁竖向温度梯度模式进行设计计算，结果更偏于安全。太阳辐射计算模型方面，李锦萍等［5]基于北京地区的太阳辐射实测数据修正了ASHRAE 模型，提出了北京晴空模型，Al-Senea等［6]通过当地实测数据修正得到了Riyadh 晴空模型，鲜有学者提出能够直接应用于青藏高原地区的晴空模型。

目前，国内外学者对钢-混凝土组合梁的温度场，尤其是青藏高原地区钢-混凝土组合梁温度场研究很少。因此，本文以某钢-混凝土组合梁桥为实例，确定了适用于高原气象条件的太阳辐射计算模型，对青藏高原大气透明度系数进行分析；建立了有限元模型，对典型时段的日照温度场进行时变分析；对铁路规范中关于板厚温差的规定对高海拔地区设计的适用性进行了评价。

1 温度时程分析基本原理

根据傅里叶导热定理，笛卡尔直角坐标系下三维瞬态导热微分方程的一般形式为［7]

式中：T为结构某一位置处的温度函数；τ为时间；x，y，z为三维坐标；ρ为结构密度；c为结构比热容；λ为导热率。

桥梁沿纵向的温度梯度可以忽略，因此可按平面问题计算温度场计算，式（1）用二维热传导方程表示为

在日照作用下，钢-混凝土组合梁结构与外界的热交换，不仅来自太阳的热辐射，也有与空气之间的热对流，因此其边界条件包括第二类和第三类边界条件两种情况的组合，可以表示为

式中：h为对流换热系数；Ta为物体边界大气温度；q为热流密度；n为法向量。

对于边界复杂的问题，式（2）的解析解求解过程十分繁琐，不便于工程人员使用。可利用有限元软件进行组合结构温度场的瞬态分析，得到温度场随时间的变化规律，总结出简化的公式与参数为工程设计提供参考。

2 钢-混凝土组合梁日照温度场仿真分析

以某钢-混凝土组合梁为分析对象，横截面见图1。钢梁部分采用开口型钢板梁，钢板梁高4000 mm。桥面中心线处混凝土桥面板厚350 mm，翼缘板边缘厚200 mm，翼缘板悬出长度2700 mm。

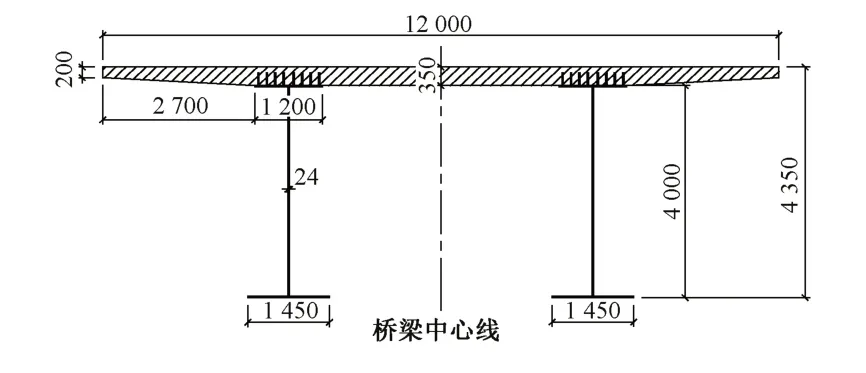
图1 钢-混凝土组合梁横截面（单位：mm）

2.1 太阳辐射计算模型

自然环境中混凝土桥梁受到太阳直接辐射、散射辐射、地面反射辐射。直接辐射和散射辐射最为复杂，常用的计算模型主要包括ASHRAE 模型、Hottel 模型［7]和幂指数模型3 种。ASHRAE 模型主要参数是根据美国太阳辐射的实测数据得到，具有典型的地域特征；Hottel模型于1976年提出，通过计算太阳直射透射比和散射透射比计算直接辐射和散射辐射，计算参数基于经验系数获得，其主要影响因素为太阳高度角和海拔高度，一般适用于能见度高于23 km，海拔低于2500 m的情况，对于高海拔地区并不适用。

Hottel［8]在对混凝土桥梁温度应力的研究中，基于激光器的朗伯特定律提出了采用幂指数模型计算到达地表的太阳直接辐射强度。法向直接辐射和水平散射辐射分别为

式中：Id为太阳直接辐射强度；IH水平散射辐射强度；I0为太阳常数；P为大气透明度系数；qa为水蒸气、臭氧、氧气和水溶胶对辐射吸收系数。qa，P均可通过实测得到。

幂指数模型考虑了海拔、大气透明度系数等对短波辐射的影响，在高海拔和空气稀薄的青藏高原地区较为适用。故本文选用幂指数模型作为高海拔地区铁路钢-混凝土组合梁温度场分析的太阳辐射计算模型是合适的。

2.2 青藏高原地区大气透明度系数

太阳辐射从大气上界进入大气层后受到大气透明度的影响，大气透明度的特征量用透明系数P表示。目前大气透明度系数P有两种计算方法，分别是基于均值气象条件和极值气象条件得到的拟合公式。

①翁笃鸣等［9]根据累年实测气象数据均值分析拟合提出的计算公式，表达式为

式中：e为水汽压，102Pa；α，γ为经验系数，α主要反映空气分子和灰尘的影响，γ主要反映水汽的影响；k为相对大气压，与海拔相关，位于海平面时k取1。

根据对青藏高原及其邻近地区不同海拔高度的27个站点资料分析［9]，拟合得到α为0.389，γ为0.0112。

②凯尔别克［7]和Elbadry 等［10]提出的基于极值气象条件的复合大气透明度计算方法，表达式为

式中：tu为林克氏浑浊度系数，随大气状况和季节变化，可按下面经验公式计算

式中，Am，Bm为经验参数，分别表示不同大气状况下，林克氏浑浊度系数的年平均值和变化幅度，其值见表1。

表1 林克式浑浊度系数

根据式（6）和式（7）计算得到的不同海拔高度的大气透明度系数，见表2。可见，山区大气透明度系数比工业区平均增加了7.2%～19.6%，按照山区极值气象条件计算的大气透明度系数比按照青藏高原气象条件均值计算得到的大气透明度系数增加了7.9%～21.4%，且海拔越低相差越大。按照式（6）计算的青藏高原大气透明度系数与式（7）计算的工业区大气透明度系数相当。

大气透明度系数随海拔升高成线性增加（图2），线性相关系数大于0.999。均值气象条件下，海拔每升高1 km 大气透明度系数增加0.035；极值气象条件下，海拔每升高1 km大气透明度系数增加0.024。

表2 不同海拔高度的大气透明度系数

图2 两种计算方法的青藏高原大气透明度系数

2.3 有限元模型

建立钢-混凝土组合梁平面有限元模型，单元尺寸20 mm，见图3。桥梁呈南北走向，经度E91.00°，纬度N29.67°。大气透明度系数取0.834，计算对流换热系数时，取该地区8月最小平均风速1.56 m/s，气温按照该地区累年6月份日均最高气温和最低气温的正弦变化曲线取值。材料热力学参数见表3。

图3 有限元模型

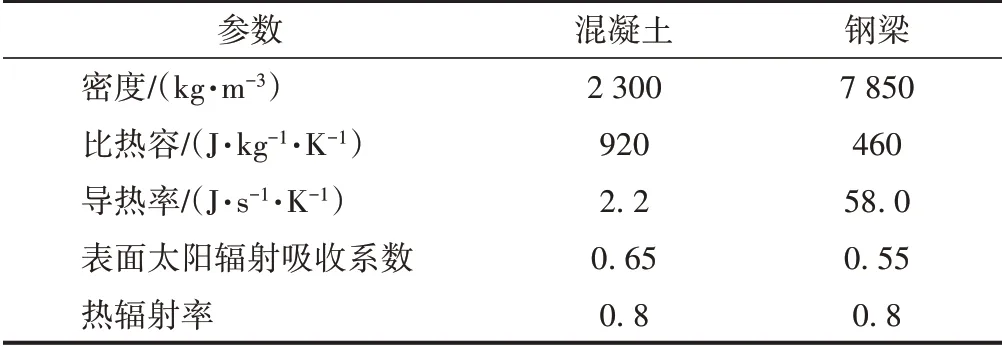
表3 材料热力学参数

2.4 计算结果分析

通过有限元计算得到了夏至日06：00—19：00 的钢-混凝土组合结构瞬态温度场，混凝土桥面板最高温度出现在14：00，14：00 结构的温度场云图见图4。可见，温度梯度最大的区域位于钢主梁附近的混凝土桥面板。

图4 14：00钢-混凝土组合梁温度场云图（单位：℃）

06：00—19：00东侧钢主梁中心线处温度场与混凝土桥面板板厚温差见图5。可见，钢-混凝土组合梁日照温差主要分布在混凝土板厚范围内，钢主梁的温度在腹板高度方向上的温度梯度较小，除上、下翼缘板附近，腹板的温度梯度几乎为零；由于钢主梁的存在，使得钢梁中心线处的板厚温差大于桥面中心线处的板厚温差，分别为27.9，19.0 ℃；钢主梁中心线处板厚温差最大值出现在14：00，桥面板中心线处板厚温差最大值出现在13：00。

图5 钢-混凝土组合梁日照温度场

东侧钢梁中心线处和桥面板中心线处06：00—19：00沿板厚温度场见图6。可见，2 个位置处桥面板顶面温度最大值相当，分别为49.3，50.3 ℃，分别出现在14：00，15：00。由于钢主梁导热系数大、比热低，与钢主梁接触的混凝土温度较低，使得钢梁中心线处的混凝土桥面板板厚温差明显大于桥面板中心线处的板厚温差。

图6 混凝土桥面板温度场

3 铁路规范适用性评价

目前专门针对铁路结合梁的温度荷载取值可参考的规范仅有TBJ 24—1989《铁路结合梁设计规定》［11]，且规定较为笼统。另外还可参考TB 10092—2017《铁路桥涵混凝土结构设计规范》［12]，对于混凝土箱梁沿板厚方向温度梯度的规定。

TBJ 24—1989 规定：在缺乏足够的技术资料时，可认为在梁和板内的温度在各自高度范围内为一定值，其差值可用±15 ℃。

TB 10092—2017 对不同的板厚分别规定了温差曲线指数a′，a′按表4取值［11]。

表4 不同板厚温差曲线指数a′取值

箱梁沿板厚的温差曲线计算式为

式中：T′y为计算点y处的温差；T′0为板内外表面温差。

由图5 可知，根据拉萨地区极值气象条件计算得到的钢-混凝土组合梁中混凝土桥面板存在较大的温度梯度，故TBJ 24—1989 用于高海拔地区钢-混凝土组合梁存在一定的局限性。根据式（9）拟合得到桥面中心线和钢梁中心线处温差沿板厚的分布曲线，见图7。可见，由于式（9）主要用于铁路混凝土箱梁的设计，故桥面中心线处的板厚温差按照a′=10 拟合得很好，相关系数为0.989。而钢梁中心线处由于钢梁材热参数的影响，板厚温差按照a′=7 进行拟合，相关系数为0.987。

图7 钢-混凝土组合梁日照板厚温差拟合曲线

TB 10092—2017 中给出的大气透明度系数最大为0.80，大气透明度系数每增加0.1，竖向温差增大约2 ℃。由表2可知，极值和均值气象条件下拉萨的大气透明度系数分别为0.834，0.736。大气透明度系数对钢-混凝土组合梁日照板厚温差的影响见图8。

图8 大气透明度系数对钢-混凝土组合梁日照板厚温差的影响

由图8 可见，板厚温差与大气透明度系数成线性关系。在桥面中心线处，大气透明度系数每增加0.1，板厚温差1.9 ℃，与TB 10092—2017 吻合；在钢梁中心线处，大气透明度系数每增加0.1，板厚温差3.3 ℃，大于TB 10092—2017的规定（2 ℃）。

4 结论

通过对高海拔地区某钢-混凝土组合梁桥典型时段、典型气象条件下的日照温度场时变分析，并与规范进行对比验证，得到以下结论：

1）太阳辐射模型中的幂指数模型在高海拔和空气稀薄的青藏高原地区更为适用。

2）钢-混凝土组合梁日照温差主要分布在混凝土板厚范围内，钢主梁的温度在腹板高度方向上的温度梯度较小；由于钢主梁的存在，使得钢梁中心线处的板厚温差大于桥面中心线处的板厚温差。

3）钢-混凝土组合梁板厚温差符合TB 10092—2017《铁路桥涵混凝土结构设计规范》中的指数模型分布，a′的取值略有不同。

4）钢-混凝土组合梁板厚温差与大气透明度系数成线性相关关系。