带时间窗农机调度问题的改进遗传算法
吕云杰,郭 辉,鲁 东
(新疆农业大学,新疆 乌鲁木齐830000)
0 引言
农机调度问题实质上是一类多因素控制的车辆调度问题,属于多目标组合优化问题。本文针对农业合作社服务范围内的农田作业时间、作业地点等因素,以农机和农田作业点之间的组合优化问题展开研究。
目前,国内外建立了比较完善的农机社会服务体系。VanElderen 提出在农业生产领域有纯粹调度和连续调度两类基本的调度问题[1]。Bochtis 和Sorensen[2-4]为农业领域的VRP 问题提出了专用的操作方法来解决田间作业的规划和调度问题。在国内,如王增建立了在时间窗限制条件下的资源损失最小化和时间方差最小化的多目标应急物资调度模型[6]。王雪阳采用单个染色体指定位置交叉变换来降低不可行解的数量的方法求农机转移成本最低[8]。王玉巍采用自然数编码、染色体随机交叉的方式进行农机调度问题优化[9]。上述文献主要研究的是一个农机服务组织为多个农田服务的农机调度问题,没有综合考虑带时间窗农机调度问题的影响因素,本文在详细思考以上文献的基础上更加全面的考虑了农机调度问题影响因素。
1 问题描述与数学模型
1.1 问题描述
本文研究的农机调度问题可描述为:某农机服务组织在一定的服务范围内拥有多个不同位置的农机库,每个农机库拥有多种不同型号的农机,需要给分布在不同位置的农田提供农机作业服务,每台农机按照调配路线逐次作业,对于同一个农田作业点,该农机只能到达一次。每个农田的位置、面积、作业时间窗以及所需农机型号均已知。
1.2 数学模型的构建
1.2.1 变量说明
针对构建的农机调度数学模型,为了方便描述,对模型中相关变量做如下说明:
k,m,j 分别表示农机编号、农机库编号和农田编号;Aj—农田j的面积,j=1,2,···n;—农机作业时的单位面积作业成本;—农机转移时的单位时间消耗成本—农机等待时的单位时间等待成本—在编号为m的农机库中,编号为k的农机从农田i到农田j所用的转移时间,其中i≠j,且i=0,1,2···n;j=0,1,2···n;—m农机库中的k农机从农田i转移到达农田j时的时间节点;[bj,ej]—农田j的作业时间窗,bj代表农田j允许作业的开始时间,ej代表农田j允许作业的最晚完成时间—农机k在农田j作业的完成时间—农机k完成农田j任务的作业时长。
1.2.2 目标函数
本文以调度总成本低、准时性高和农机调度数量少为农机调度目标,构建多目标组合优化问题的农机调度模型,其步骤如下:
(1)农机调度成本
农机作业成本:

农机运输成本:

农机等待成本:
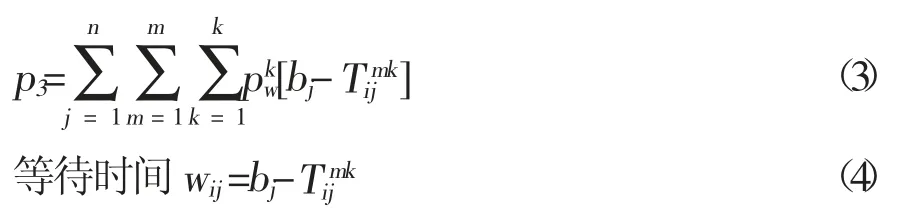
其中,i=0,1···n,j=0,1···n。
农机调度总成本:

(2)农机调度总数
农机调度总数是指在一次农机调度过程中,各农机库派出的所有农机的数量,其函数表达式如下:

1.2.3 约束条件
(1)在一次农机调度过程中,每个农田作业点j有且仅有一台农机为其服务;

(2)在农机调度路线上,相邻两个农田作业点的时间约束关系,考虑了在前一个农田作业点准时完成作业的情况下,仍能保证下一个农田作业点能够准时作业;

(3)在一次农机调度过程中,农机k在农田作业点i完成作业服务后到达农田作业点j的时间是否小于农田作业点j允许作业的开始时间,若是,则wij=1,否则为0。

1.2.4 多目标处理
本文以调度成本最低且配发农机数量最少为调度目标,为了使求解步骤简化同时方便在解集空间上搜索,故采用极差值法将两个目标函数进行优化组合,得到如下综合目标函数:

其中,minX表示农机调度过程中总成本最低且配发的农机数量最少。
2 自适应遗传算法设计
2.1 染色体编码
本文基于农田进行染色体整数编码,该编码方式能够清楚的表示农机来自哪个农机库、农机编号和作业路线。染色体编码设计为R=(m1,m2···mi),每个基因mi包含了三个参数:农机库编号M、农机编号K 和农机出行路线,基因序列mi表达的关系是编号为i 的农田由编号为M 的农机库配发编号为K 的农机对其作业。初始种群的初始解编码是在一定范围内随机产生的,即M∈[1,2,3···m],K∈[1,2,3···k]。
2.2 遗传操作设计
(1)选择算子
本文中选择算子采用轮盘赌选择法实现,根据每个个体的适值进行择优,并采用最优保存策略,将适应值最大的染色体直接复制给下一代,以保证将优良基因不丢失,从而使得结果能收敛为全局最优。对于种群大小为m,适值为fi(x)的第i个个体被选择的概率如下公式:

(2)交叉算子
为避免过多的基因交换,经过综合考虑求解问题和染色体编码方式,设计如下交叉方式:
设定初始种群规模后,任意取两条染色体p、q 作为父代,并随机生成两串长度等于每组路径上的农机数的二进制数并作为两组路径的掩码T1、T2,将掩码的各位与路径一一对应,其中“1”所对应的路径直接复制给下一代,而“0”对应的路径,找到另一个染色体子代路径中与服务该农田相同的农机库编号和农机编号,则将该农田插入到子代的这条路径中,如果另一个染色体子代中没有与服务该农田相同的农机库和农机编号,则该染色体在子代中继续保留服务该农田的农机库和农机的对应信息。
(3)自适应遗传算子改进设计
本文采用了由种群进化状况来确定交叉概率pc和变异pm的自适应方法,对于适应度高于种群平均适应度的个体,选择较小的pc和pm,从而保护优良个体,对于适应度低于群体平均适应度的个体选择较大pc和pm,从而扩大优秀个体生成。自适应算子的设计如下:
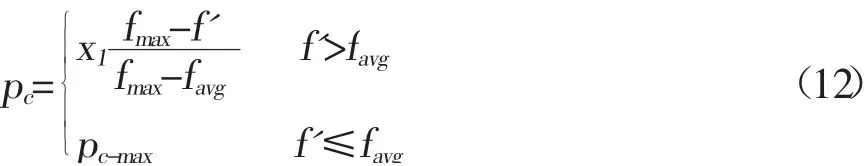
式中pc-max—最大交叉概率;pc-min—最小交叉概率;f'—交叉操作中较大个体的适应度值;fitavg—当前迭代过程中全部染色体适应度的平均值,x1—0~1 之间的常数。

式中pm-max—最大变异概率;pm-min—最小变异概率;f—变异个体的适应度值;fitavg—当前迭代过程中全部染色体适应度的平均值,x2—0~1 之间的常数。
3 仿真案例与结果分析
3.1 案例计算
本文研究对象是面向订单的多农机点服务多农田的农机调度问题,为了验证本文算法的有效性,采集新疆沙湾县宏基农机服务专业合作社的实际数据,选取合作社中两个农机库进行实例计算,并根据沙湾县农田、农机信息拥有量统计年鉴[10-11]和GPS 定位得到表1~表4 的数据。

表1 农机库信息
该合作社主要以面向订单的农机调度模式对表3 中11 个乡镇进行农田作业服务,现将沙湾县的11 个乡镇抽象为11 个需要农机服务的农田订单,其农田位置、作业面积和作业时间窗信息以及农田间距离如表4 和表5。假设农机调路程全为直线距离,各种型号农机运行速度如表3,现求农机调度成本最低且所配发的农机数量最少。

表2 农机信息
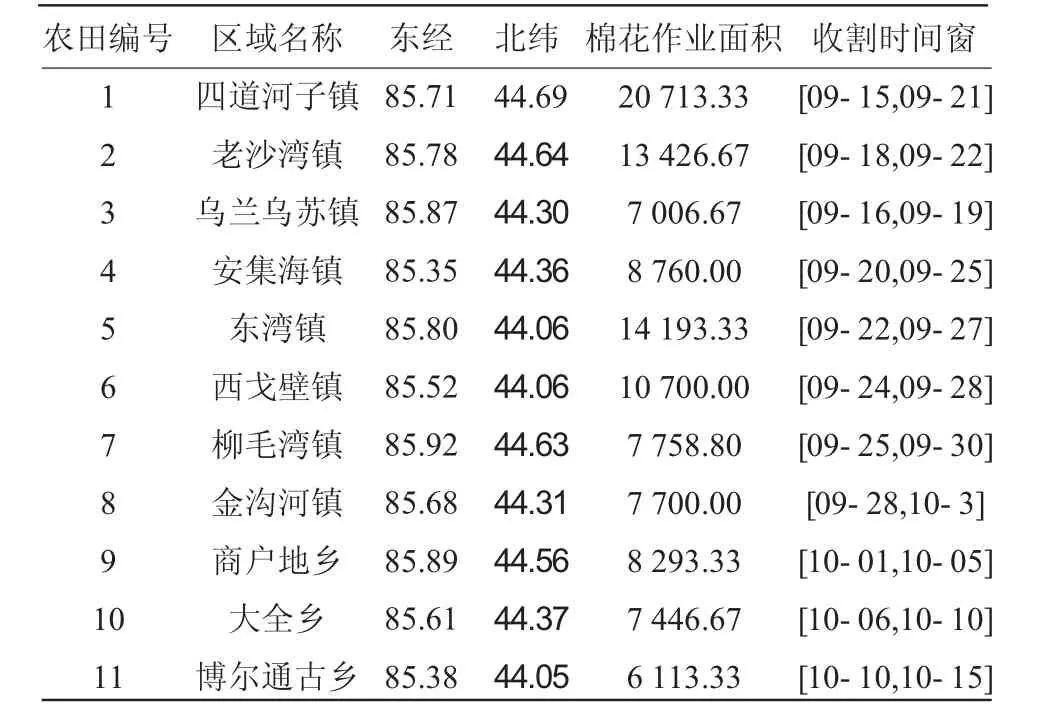
表3 农田信息
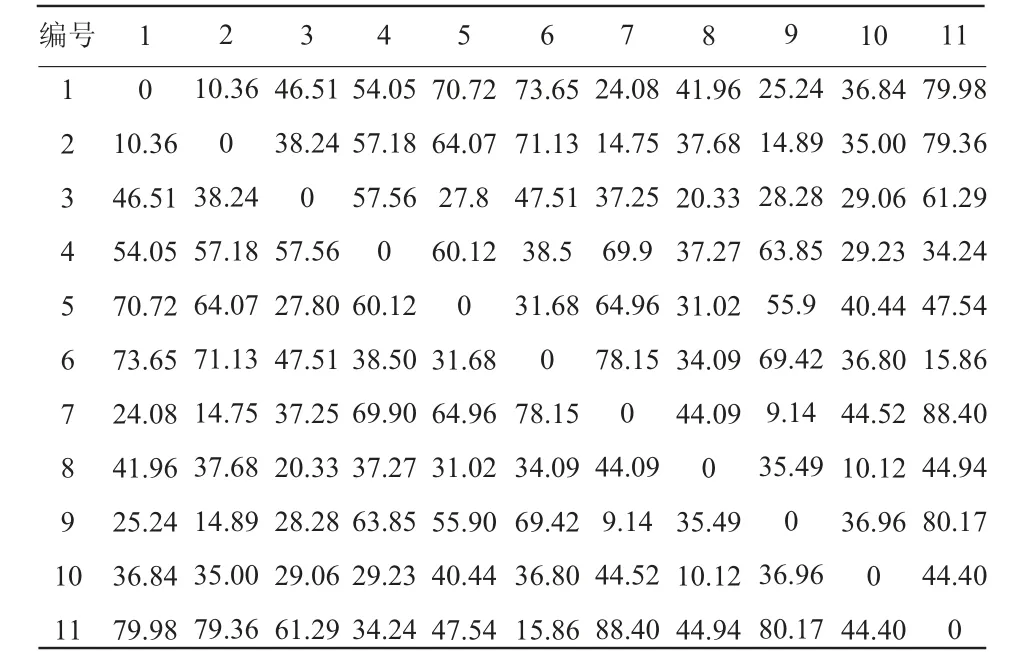
表4 各区域间的距离
3.2 结果分析
针对本案例农机调度问题,应用Matlab 对本文算法和文献算法进行编程仿真比较。并对遗传算法的参数设置如下:种群规模N=60,最大遗传迭代次数Gen=200,并且经过多次试验结果分析,其他参数取值为:x1=0.6,=0.8,最大和最小交叉概率分别为pc-max=0.9,pc-min=0.4,最大和最小变异概率为pm-max=0.1,pm-min=0.01。编程得到仿真结果(图1)。
图1 是使用本文算法计算的一次运行结果显示,M1号农机库各农机最优路线分别是:1 号农机6-5-7,2号农机4-2;3 号10;M2号农机库各农机最优路线分别是:1 号农机1-3,2 号农机8-9,3 号农机11,本次调度的最优值是164.7 元,最少配出的农机数量是6 台,对应的最优染色体为:

3.3 算法有效性分析
算法有效性分析过程:分别使用本文算法和文献9 中的算法计算综合目标函数值,若值越小,则算法性能越好;若值越大,则算法性能越差,图1 为目标函数值随遗传代数的变化。

图1 目标函数值随遗传代数的变化
从模拟实验得出的结果可以看到,本文改进后的算法与文献[9]中的算法相比较,能够得到更优的目标函数,并且能够更早的收敛于最优解,从图中可以直观的看到,当遗传算法的迭代次数设置为200,种群规模为80,遗传算法在迭代次数为0-22 和65-200 之间时,本文提出的改进遗传算法的调度成本和所需配发农机数量明显小于文献,能够得到更好的农机调度方案,能够更快地收敛于最优解,从而验证了本文改进后算法的可行性和有效性。
3.4 农田数量对算法性能的影响
当农机数量确定,农田数量由5 增加到11 时,分别应用本文算法和文献中算法计算农机调度成本,实验结果如表5 所示。
分析表5 可以看出,随着农田数量的增加,本文算法相比文献算法,调度成本降低更快,平均费用也有所降低,本文算法比文献算法平均提高了6.0%,实验结果表明:当农田维数变化,农机数量确定时,本文算法比文献算法性能好。
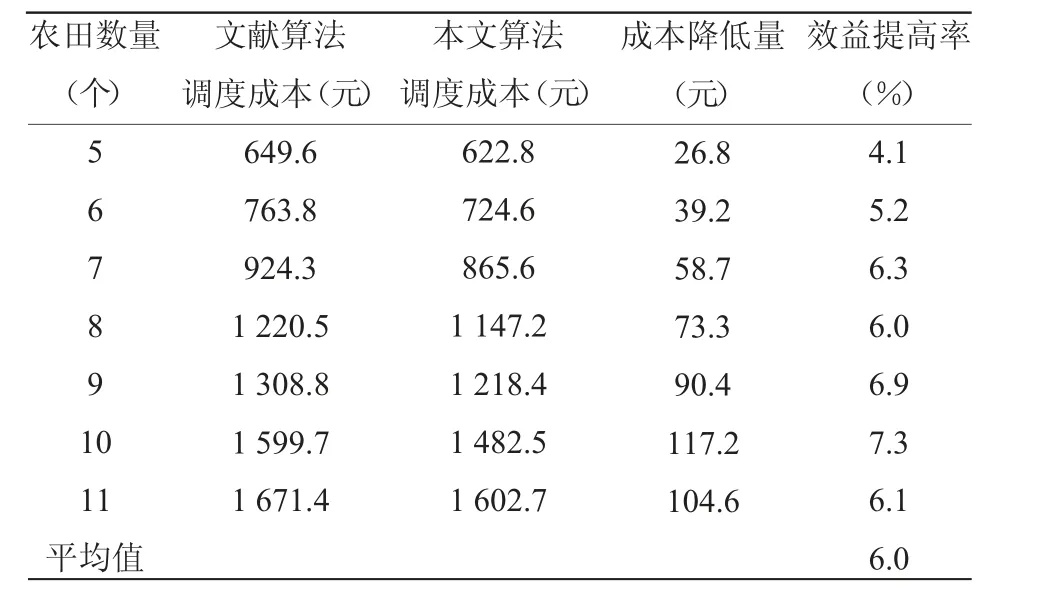
表5 农田数量变化测试结果
4 结论
针对带时间窗的多农机点服务多农田的农机调度问题,首先构建了农机调度数学函数模型,然后设计了符合农田作业收割时间窗的染色体编码方式和改进的自适应遗传算法,并利用沙湾县宏基农机服务专业合作社的实际农机数据情况进行了模拟实验,比较了本文算法和文献中算法的稳定性,验证了本文算法的有效性和可行性。最后在农田数量变化农机数量确定和农田数量确定农机数量变化的两种条件下,比较了两种算法的性能,实验结果显示本文算法性能优于文献中算法。

