巧设思维障碍 引发深度思考

陈光明

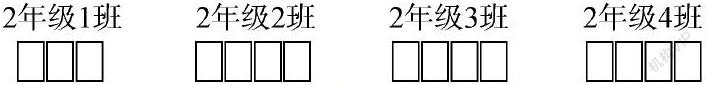
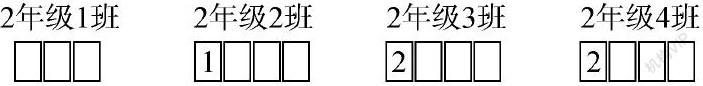
摘 要：在教学中设计富有趣味性、挑战性和开放性的问题，是引导学生进入深度思考的基础。为此，笔者常常在教学过程中故意制造一些“麻烦”，设置一些“障碍”，“逼着”学生“跳一跳，摘桃子”，带着学生“多走一些弯路看风景”，获得良好的教学效果。

关键词：巧设障碍;深度思考;隐藏关键数据;掩盖计算过程;不给足够学具

在教学实践中可以发现：问题的挑战性，直接影响着探究空间的大小，也影响着学生探究的兴趣和热情。在教学中设计富有趣味、又不失挑战性的开放性问题情境，是引导学生进入深度思考的基础。为了更好地激发学生的探究热情，引发深度思考，笔者常常在教学过程中故意制造一些“麻烦”，设置一些“障碍”，“逼着”学生“跳一跳，摘桃子”“多走一些弯路看风景”，获得良好的教学效果。

一、 隐藏关键数据，点燃思维火花

在引导学生探究规律时，免不了要借助各种数据信息。有时为了激发学生的思维，笔者故意先将问题中的关键数据隐藏起来，反而收到意想不到的效果。例如，在教学《万以内数的大小比较》时，笔者没有在一开始就为学生提供完整的数据信息，而是根据“大小比较”的三个要点，先将数据信息隐藏，然后分层次逐步呈现，来引导学生经历探究万以内数的比较过程，使学生不仅学会大小比较的方法，还明白其中的道理。具体过程如下：

环节一：位数不同，比位数。

师：二年级四个班级开展“回收饮料瓶，争当环保者”活动。哪个班级收集的饮料瓶最多，将获得“环保先锋”的荣誉称号。要想知道哪个班级收集的饮料瓶最多，你需要了解哪些信息？

生：需要知道每个班级收集的饮料瓶数量。

屏幕上出示二年级四个班级收集的饮料瓶“数量”，可是将所有的数字，用卡片遮住，只能看出每个数有几位数。

师：你会比较它们的大小吗？

所有学生一时陷入沉思，但不久就有学生举手。

生：2年级1班收集的饮料瓶数量是最少的。

师：为什么没有告诉你具体的数量，你就能知道2年级1班是最少的，你能说明其中的道理吗？

生：2年级1班收集的饮料瓶数量是三位数，其他三个班级收集的饮料瓶数量都是四位数，三位数比四位数小。

师：为什么三位数就一定比四位数小呢？

经过学生独立思考后，再组织讨论交流，使学生明白：三位数最多是999，而四位数最少是1000，所以三位数一定比四位数小。

环节二：位数相同，先比最高位。

师：其他三个班级的位数都相同，该如何比较它们的大小呢？

生：需要翻开遮盖在数字上的卡片。

师：如果现在只给你三次机会，让你翻开三张数字卡片，你会选择哪三张？

经过讨论，学生一致认为应该翻开三张“千位”上的卡片。

师：现在你又有什么新的发现？

生：我知道2年级2班收集的饮料瓶一定比2年级3班和2年级4班少。

师：为什么只凭三张卡片，你就能确定2年级2班比其他两个班级少？

通过讨论交流，使学生明白：2班收集的饮料瓶最多只能是1999，而3班和4班最少也有2000，只要看千位上的数就能比较它们的大小。

环节三：最高位相同，依次往下比。

师：现在只剩下3班和4班了，哪到底谁多谁少呢？你还需要知道什么信息？

生：只要知道它们百位上的数就可以。

教師出示3班和4班的“百位”上的数。

师：现在你能比较吗？

生1：3班收集的饮料瓶比4班多。

生2：4班最多只能是2199，而3班最少是2300。

通过先将数据隐藏，然后随着问题的探究来逐步呈现。这样极大地增加了探究的空间，为深入理解大小比较的方法和道理提供了有效的情境。同时也充分“吊足”学生的胃口，使学生在经历“探案”般的探索过程中，注意力高度集中，思维被不断引向深入。使学生在沉浸式的思考中主动获得知识与技能，不断发展思维能力，充分享受成功的喜悦。

二、 掩盖计算过程，探究错误原因

学习的过程实际上就是一个不断修正错误的过程。如何正确处理学生在学习过程中出现的错误，往往考验着一个教师的教学艺术水平。在教学《两位数乘两位数》时，练习中发现学生的一个错例。笔者故意将该生的计算过程用卡纸遮掉，问学生：“你们觉得，这道题的计算结果正确吗？说说你判断的依据。”

生1：这道题的计算是错误的，因为20×10就等于200，而24比20大，12比10大，所以正确的积一定比200大。

师：这位同学懂得用估算的方法来判断结果是否正确，他的方法值得我们每一位同学学习。

生2：两个因数的个位分别是“4”和“2”，所以积的个位一定是“8”，而他计算的结果个位上的数字是“2”，所以我断定他算错了。

师：这位同学懂得根据因数和积个位上的数来判断计算的结果，也是一种不错的方法。那么，你们猜猜看他可能错在了哪里呢？

生3：我看到他的最后结果是两位数，所以我觉得他在计算10乘24时，积的最低位没有从十位写起，而是从个位写起。

随即，笔者揭开遮盖在竖式上的卡纸，并肯定了学生的判断。

将错例的计算过程先暂时遮掉，让学生根据结果判断计算正误、反推错误原因，似乎是故意给学生的思维设置“障碍”，但却能为课堂提供了更大的探究空间。这样，不但有助于学生对错误的算法印象深刻，也为引导学生经历从多角度验证计算的正确性创造了可能，并在探究的过程中使学生的推理能力得到了发展。

三、 不给足够学具，经历柳暗花明

由于小学生思维的特点，在小学数学教学过程中，常常要借助直观学具的帮助。但有时为学生准备“太过充足”的学具反而会阻碍学生思维的发展，并不利于教学目标的实现。在教学《长方形和正方形面积的计算》时，笔者给每个学生准备了7个边长1厘米的小正方形，用来测量如下6个图形的面积。（单位：厘米，在给学生的图形上没有标出各条边的长度。）