不同推进器配置下半潜式平台动力定位能力
尚勇志,崔亚昆,薛海波,赵 亮
(1.上海雄程海洋工程股份有限公司,上海 201306;2.上海交通大学 海洋工程国家重点实验室,上海 200240)
0 引 言
为了海上油气勘探和生产向更深的海域迈进,浮式生产储卸油装置(Floating Production Storage and Offloading,FPSO)和半潜式平台等被广泛应用。动力定位系统(Dynamic Positioning System,DPS)通常用于将海上船舶自动地保持在要求的位置上以进行安全作业。动力定位(Dynamic Positioning,DP)船被国际海事组织(IMO)和各船级社(DNV、ABS、LR等)定义为完全通过推进器自动保持其位置和艏向(固定位置或预定轨迹)的船舶。过去五十年来,DPS已被广泛应用于各类海洋工程船舶。
海洋结构物海上作业安全始终是新型DPS设计与工作中的首要考虑因素。国际海事承包商协会(IMCA)认为,动力定位能力分析可以确定DPS在给定艏向下所能抵抗的最大环境力[1]。因此,为了安全地执行操作,获知并分析船舶的动力定位能力是必不可少的[2]。目前,0°~360°艏向的船舶动力定位能力为大多数动力定位能力分析的主要方向。比如,王亮[3]对某半潜式平台进行动力定位能力分析,以验证新设计的DPS的性能。徐胜文等[4]开发了一种半潜式平台在推力器失效模式下的定位能力程序,并对该程序中的推力分配方法进行详细的阐述。
在动力定位能力分析中,要求环境力和力矩与推力系统提供的推力和力矩达到静态平衡。对于实际的船舶来讲,其推力系统一般由几种不同推进器组成,而动力定位能力通常由推进器的最大推力及其配置决定,这是一个复杂的问题。MAHFOUZ等[5]结合推进器选型、配置,初步探究新设计船舶的动力定位能力。然而,一般意义上的动力定位能力分析与比较是基于玫瑰图进行粗略观察的,当这些玫瑰图彼此重叠时,易引起混淆。因此,有必要采用一种能够量化综合定位能力的标准来比较玫瑰图[6-7]。
本文重点研究推进器配置对综合定位能力的影响。对于3种不同的推进器配置,其推进器的数量不同,但推进系统能够发出的最大总功率相同。针对这3种推进器配置,开展动力定位能力分析,以研究不同推进器配置下某半潜式平台的综合定位能力。
1 动力定位能力分析方法
动力定位能力分析选取的坐标系固定在船体上,其原点位于水平面中的平均振荡位置,各轴的正方向分别为x轴指向船首、y轴指向左舷、z轴指向上为正。相对环境角度α以从船尾起的逆时针方向为正。力矩以逆时针方向为正。船舶固定坐标系如图1所示。
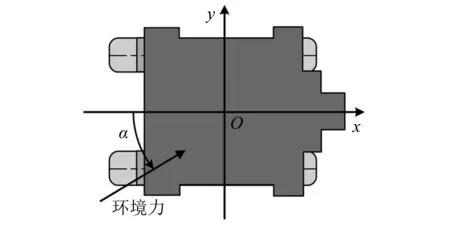
图1 船舶固定坐标系
动力定位能力分析的准确性取决于环境力的精确估计及所选择的推力分配逻辑的有效性。环境力的估计可基于模型试验、计算流体力学计算和经验公式等[8-12]。推力分配逻辑可被归纳为优化问题,其目的通常是最小化推进器所使用的功率,同时考虑推进器推力和位置约束[13-14]。文献中提供了许多优化方法开发推力分配逻辑,二次规划方法已被证明是相对有效和可靠的[15]。
在动力定位能力分析的计算中,要求环境载荷的作用力与推力系统提供的作用力和力矩平衡。其核心步骤为利用推力分配逻辑得到不同环境载荷下所需作用力和力矩的最优解,不断增大环境条件直至推力系统不能分配出结果,该情况下的环境条件即为所求的定位能力。变更艏向角,直至完成所有艏向下的计算。最后,绘成船舶的定位能力玫瑰图。
2 综合定位能力指标
在动力定位能力分析中,单一的工况可通过直接观察玫瑰图进行分析。然而,对于多个工况,在一张玫瑰图中可能会出现重叠的情况导致观察不便,哪种工况有更好的定位能力也不易判别。即使根据自己的偏好来选择更好的工况,也缺乏对定位能力稳定性等因素的定量评估。因此,量化的综合定位能力指标对于直接和准确地比较不同工况下的船舶定位能力是必不可少的。综合定位能力由总体平均定位能力和依赖艏向的船舶定位能力的稳定性决定[7]。
2.1 总体平均定位能力
工作艏向区间由艏向相对于环境条件的方向组成。工作艏向区间示例如图2所示。总体平均定位能力Ca,m为
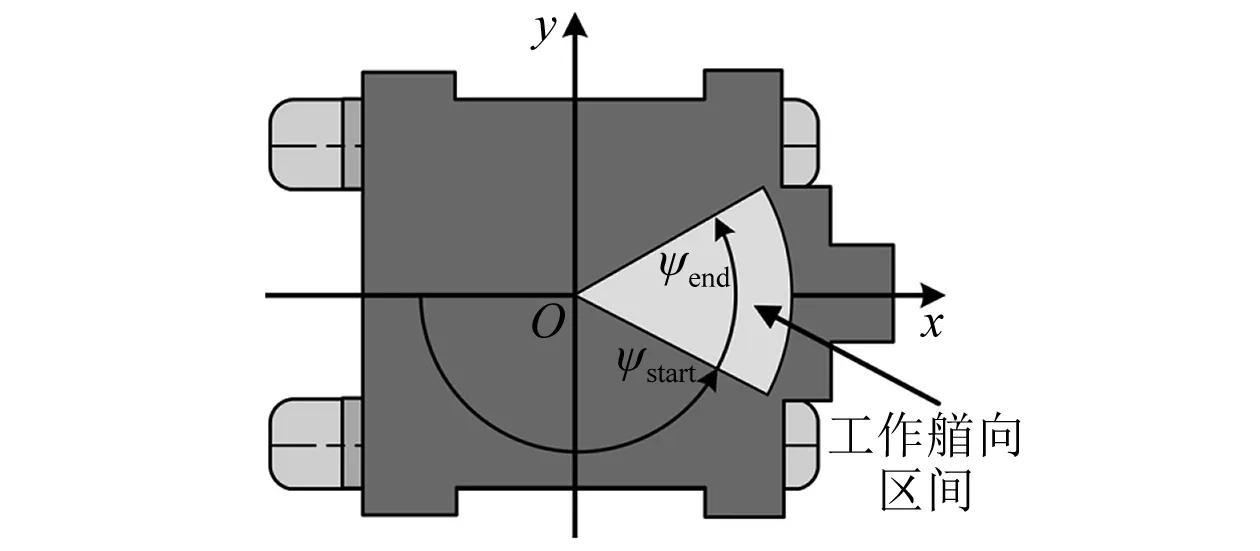
图2 工作艏向区间示例
(1)
式中:ψstart和ψend为给定工作艏向区间的起始角和终止角,以艏向的逆时针方向为正,并满足0≤ψstart<ψend≤2π;Vw(ψ)为海洋结构物在艏向ψ的定位能力,依据艏向的风速限制,可通过动力定位能力分析结果得到,通常以极坐标格式表示;P(ψ)为艏向概率密度函数,取决于环境力量的方向ψ的艏向概率密度函数。
P(ψ)可表示为
(2)
式中:P(ψi)为船舶的任意艏向;δψ为ψ的微元,δψ的量越小,得到的艏向概率密度函数越精确;Ci为在第i个艏向下,一个长时间段(如1 a)的观测中,以一个特定的频率(如每分钟统计1次)统计所得次数;M为统计中艏向的总个数。通过表1的统计数据,P(ψ)可以通过长期对艏向进行实测获得。
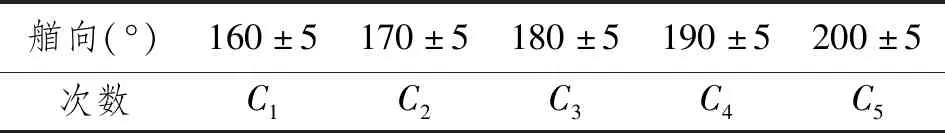
表1 艏向统计数据示例(δψ=10°)
若不能获得现场实测结果,则在给定的工作艏向区间(即在式(2)中Ci=Constant)可假定艏向的概率是恒定的。P(ψ)又可表示为
(3)
注意,式(3)为式(2)的特殊情况。
2.2 定位能力的稳定性
艏向定位能力的稳定性可由标准差和在给定艏向区间的能力期望值联合建模。定位能力的稳定性Ca,s为
(4)
(5)
式(4)和式(5)中:σ和μ分别为标准差和工作艏向区间[ψstart,ψend]中P(ψ)Vw(ψ)的期望,P(ψ)已经考虑在σ的公式中。
2.3 综合定位能力指标
综合定位能力指标由总体平均定位能力和船舶依赖艏向能力的稳定性共同决定。综合定位能力指标Ca,c为
(6)
式中:λ为Ca,c在综合定位能力指标中的权重因子。当船舶需要更高的能力稳定性以进行安全操作时,可提高λ来给综合定位能力指标的能力稳定性更大的权重。
3 推进器配置和功率消耗
推力系统能够抵抗的最大环境力取决于各推进器可提供的最大推力及其配置情况[13]。如果一艘DP船配备了m只推进器,由推力系统共同产生的广义力矢量τ∈R为
τ=(τx,τy,τN)T=B×u
(7)
式中:τx为纵荡力;τy为横荡力;τN为艏摇力矩;矢量u∈R2m包含了每个独立的推进器在船首和左舷方向上产生的力的大小;3×2m矩阵B的纵列(2i-1,2i)由式(8)给出
(8)
在采用的坐标系中,第i个推进器在水平面上的位置为(lxi,lyi)。
每个推进器的消耗功率被定义为全回转推进器产生所需推力的功率。推进器可实现的推力计算式为
T=KTρn2D4
(9)
式中:KT为推力系数;ρ为海水密度;n为转速;D为推进器直径。转矩Q可表示为
Q=KQρn2D5
(10)
式中:KQ为转矩系数。消耗功率可表示为
P=2πnQ
(11)
根据式(9)~式(11),当达到的推力确定时,就可以得出消耗功率。
4 动力定位能力分析算例
基于自主编写的动力定位能力分析程序,对分别装备有6、8、10个全回转推进器的3种不同配置的半潜式平台定位能力进行比较,如图3所示。半潜式平台的参数如表2所示。推进器的位置如表3所示。在每种工况下,推进器具有相同的特性,为保证各工况总的可使用功率相同,在推进器配置A、B、C等3种不同工况下最大可用推力分别为970 kN、800 kN、690 kN。在每种工况下推进器最大可用推力的确定是基于其所能发出的最大可用功率的,如式(9)~式(11)。在本算例中,风力、流力和力矩系数由模型试验得到。按照IMCA M140的建议,设定流速为1 kn。波浪力和力矩由计算流体力学方法估计得到。
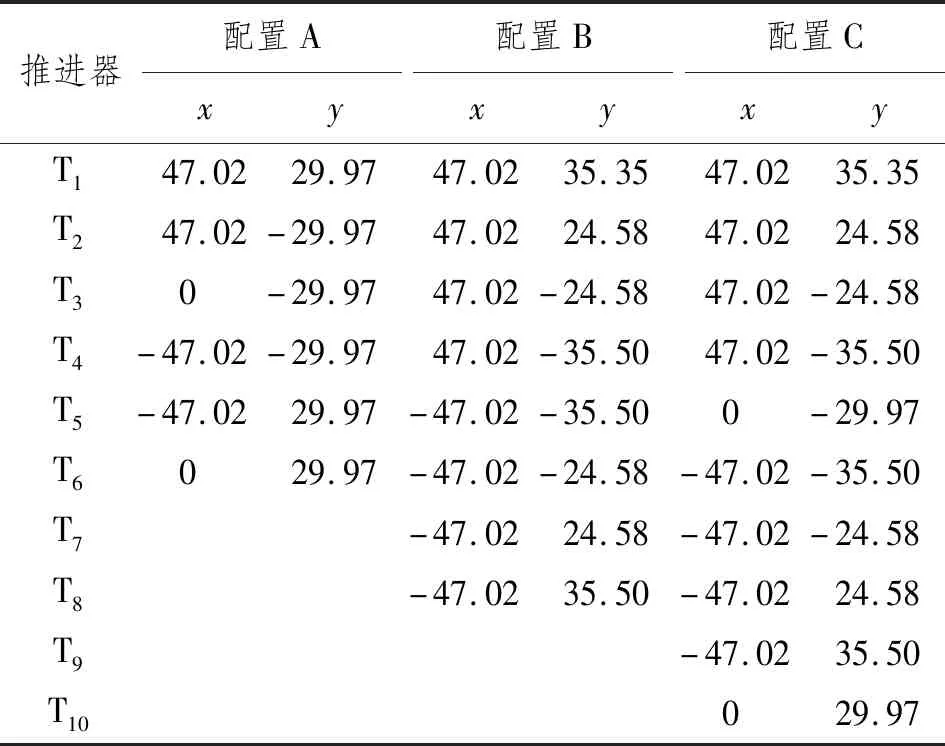
表3 推进器位置 m
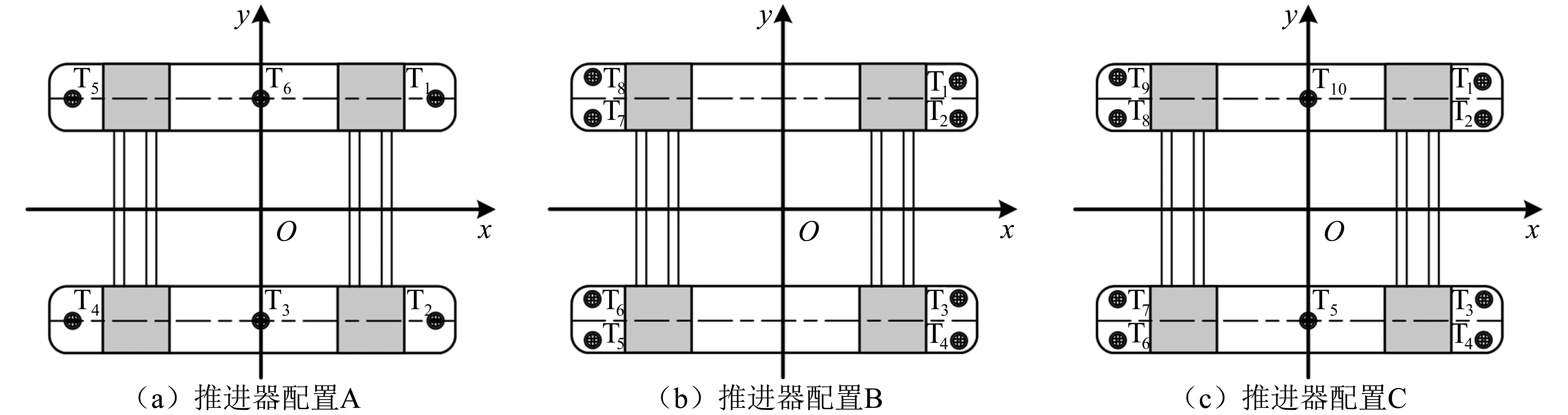
图3 同一半潜式平台的不同推进器配置

表2 半潜式平台参数
由于全回转推进器的距离较近,考虑全回转推进器之间的相互干扰。为防止推进器间的相互作用降低推力系统的性能,通常需要在推力分配算法中考虑禁止角,以禁止推进器进入相邻推进器可能受其尾流影响的扇形域[16]。各不同推进器配置设置的禁止扇形域如表4所示。
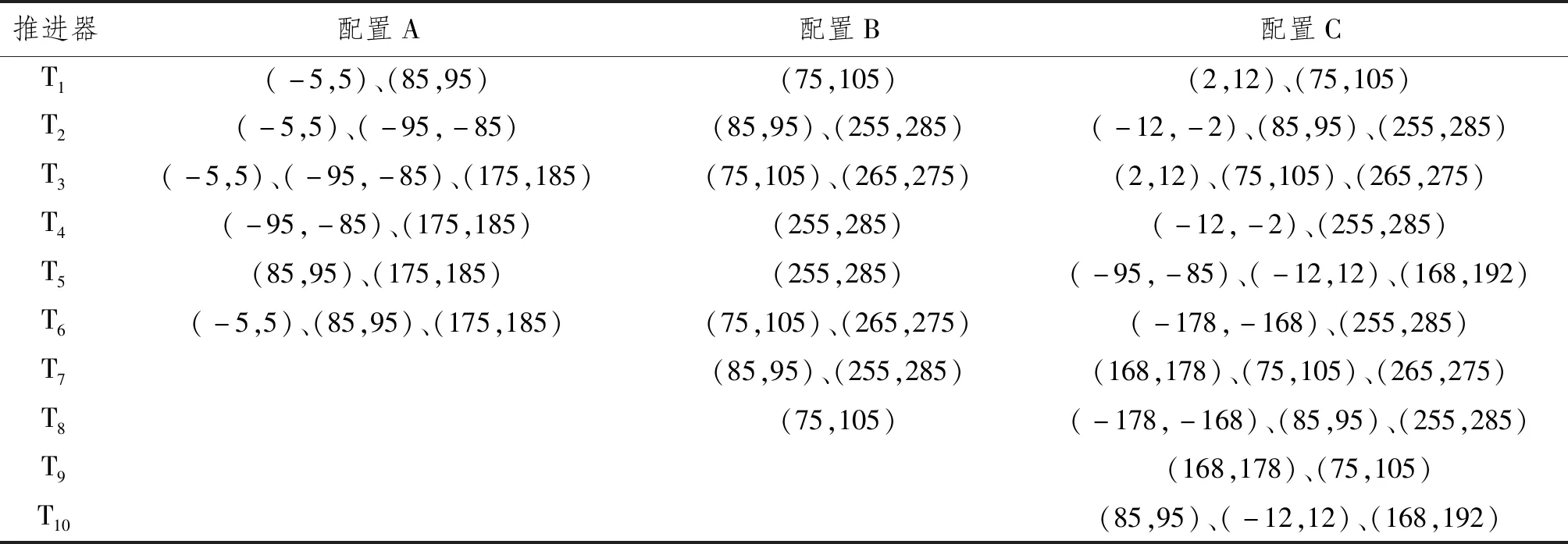
表4 推进器的禁止扇形域 (°)
5 结果与讨论
图4所示为不同工况下半潜式平台动力定位能力分析的结果。采用综合定位能力指标来量化船舶的综合定位能力。由于无法获得船舶的工作艏向概率密度函数,在所有工况下,P(ψ)=1/|ψend-ψstart|。由于无法获得实际的工作艏向区间,将工作艏向区间设定为[135°,225°]。基于综合定位能力指标,可得到量化的定位能力,如表5所示。
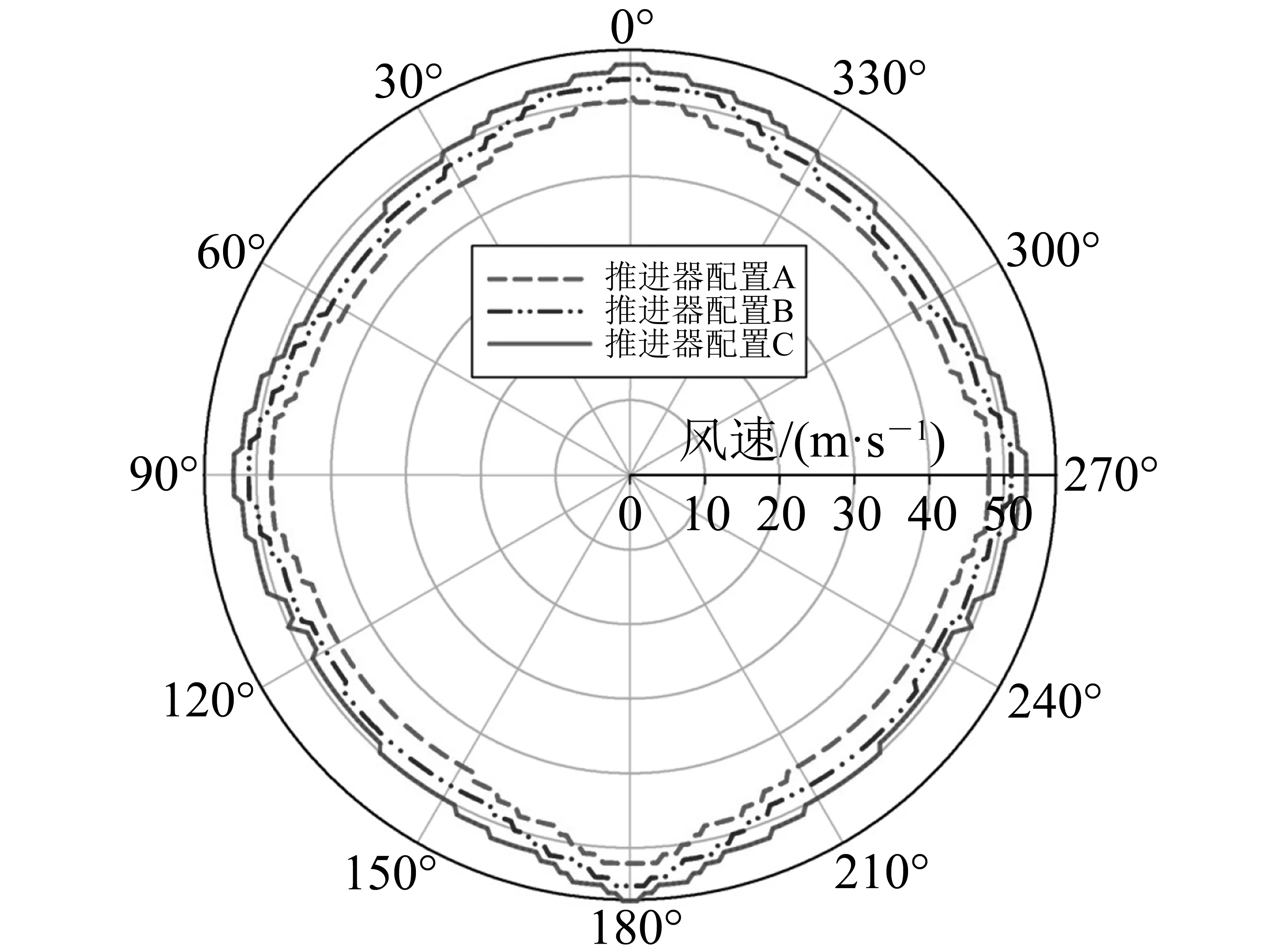
图4 不同工况下动力定位能力玫瑰图

表5 不同工况下量化的定位能力Ca,c
在图4中,推进器配置C结果的玫瑰图包含了配置A和配置B的结果。在表5中,推进器配置C工况的量化定位能力是所有工况中最大的。从该结果可以看出,推进器配置C使得半潜式平台具有最佳的综合定位能力。虽然在所有工况下的最大可用功率是相同的,但具有更多推进器的半潜式平台可以提供更多的推力。因此得出结论,具有推进器数量最多的推进器配置使得半潜式平台的定位能力最强。这是由于更多的推进器可以更加灵活地进行推力分配产生所要求的力矩。尽管如此,在3种不同推进器配置下的综合定位能力指标差异并不明显,尤其是推进器配置B,与推进器配置C相比,平台的动力定位能力约小8%。
实际上,推力系统的设计也应考虑到推进器的安装成本和船舶总布置的要求。通常,推进器配置B是半潜式平台采用的折中方案。
6 结 论
针对半潜式平台推进器系统选型问题,基于综合动力定位能力指标,对不同推进器配置的半潜式平台进行定位能力的比较。不同的推进器配置体现在布置位置和推进器数量上,但不同的配置都保持了相同的最大可用推进器功率。结果表明,具有最多推进器数量的推进器配置使得半潜式平台具有最大的定位能力,但在各工况下的定位能力差异并不明显。推力系统的设计还应考虑推进器的造价和船体总布置的要求,以及定位能力与安装成本之间的权衡。因此,在实际工程建造中通常选用相对折中的方案。

