基于ANSYS分析的带腐蚀海底管道强度计算

梁 鹏，庞洪林，万宇飞，王文光，王安达

(中海石油(中国)有限公司 天津分公司，天津 300459)

0 引 言

自20世纪70年代我国海底输油管道敷设开始，迄今海底管道的建设已有40多年的历史[1]。目前，海洋油气输送主要采用钢制管道，海洋环境复杂，管道内部有高压油气通过，外部承受风、波浪和海流载荷作用，一旦发生泄漏，可能造成巨大的经济损失和生态破坏，甚至导致人员伤亡。目前部分已投入运行的海底管道已不同程度地出现问题，尤其当海底管道进入中后期服役阶段时，损伤失效率和油气泄漏事故逐年提高。在引起海底管道失效的常见因素中，腐蚀是主要原因之一[2-3]。尽管釆取多种防腐措施，但随时间推移管道腐蚀部位壁厚减薄，管道失效概率逐渐增大[4-8]。根据腐蚀的不同位置，将腐蚀坑分为外部腐蚀坑、焊缝处腐蚀坑和内部腐蚀坑，如图1所示。本文针对内部腐蚀坑展开研究。

图1 钢质海管不同位置处腐蚀示例

从20世纪70年代以来，国外对腐蚀海底管道进行了一系列理论和试验研究，从广泛使用的ASME B31G到后来的基于全尺寸爆破试验的DNV RP-F101方法以及基于有限元分析的PCORRC等方法[9-13]，逐渐形成了腐蚀海底管道剩余强度评价规范和体系。1999年，英国燃气公司 (BG)和挪威船级社(DNV)合作开发了对含有腐蚀缺陷的管道进行评估的规范 (DNV-RP-F101)，并于2004、2010、2015年对该规范进行更新。该规范不仅可用于只有内压作用下的腐蚀缺陷评估，而且还可用于内压和纵向压应力组合作用下的腐蚀缺陷评估。DEWANBABEE[14]对内压和轴压组合作用下API 5L X46腐蚀管道的极限轴压承载力及变形进行试验和有限元模拟，为腐蚀管道的安全性评估提供指导。国内郎一鸣[15]、杨颖[16]对内压和轴力组合作用下腐蚀海底管道的极限承载力进行有限元分析，将管道最大等效应力达到极限抗拉强度的90%作为判断管道发生失效的准则，并考虑载荷加并考虑载荷加载顺序对管道极限承载力的影响。陈严飞等[17]、张小勇[18]、崔铭伟等[19]、张旭昀等[20]、冯欣鑫等[21]、卢盛灿等[22]分别对腐蚀管道剩余强度与剩余寿命和失效压力进行相关研究，对不同腐蚀深度情况下可靠度指数和失效概率进行分析，为海底腐蚀管道的风险评估提供参考。

1 管道强度理论计算公式

当管道在内压、轴向力和弯曲载荷联合作用下发生塑性变形时，管道材料表现为在多轴应力下的屈服。图2和图3分别为管道所受轴力与弯矩受力分析图，其中：D为管道外径；t为管道壁厚；F为管道所受轴力；M为管道所受弯矩；σ为管道应力。

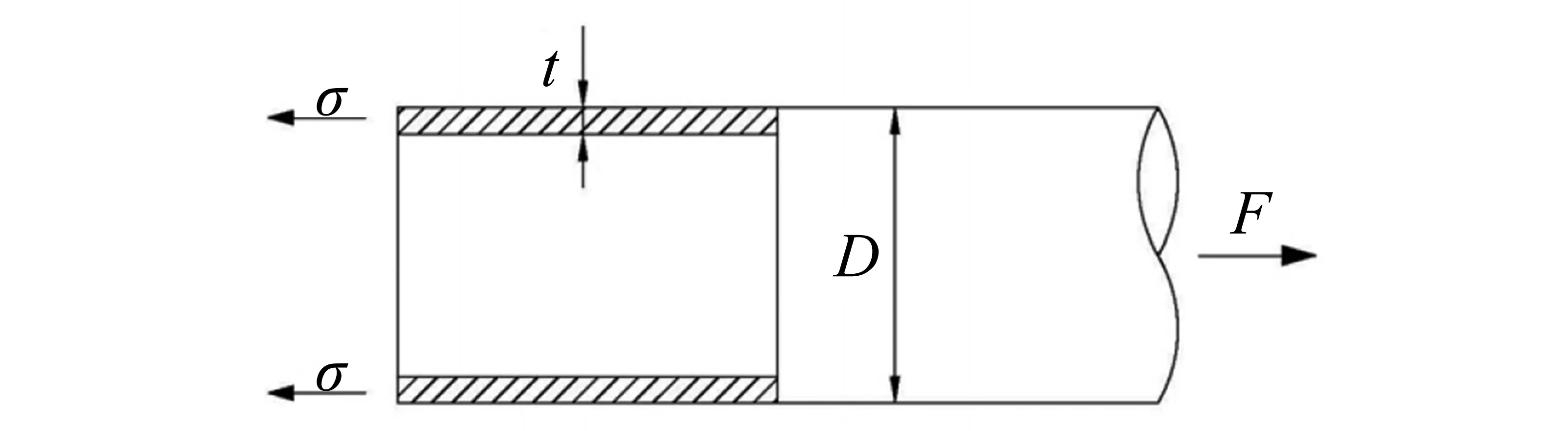
图2 管道受轴力作用下的受力分析

图3 管道受弯矩作用下的受力分析

海底管道内油气等输送介质会产生内压，内压引起的环向应力σθ为

(1)

式中：P为管道所受内压。

海底管道在敷设时和受热膨胀时会产生沿管道方向的轴力，轴力引起的轴向应力σz为

(2)

式中：A为管道横截面面积。

海底管道在发生悬跨时，会受到弯矩作用，弯矩引起的轴向应力为

(3)

式中：y为点到中性轴的距离；Iz为管道截面惯性矩。

当管道受到组合工况的载荷作用时，管道所受到的应力应遵循强度理论进行计算。关于屈服的强度理论主要有第三强度理论和第四强度理论。理论计算使用第四强度理论，公式为

(4)

式中：σ1、σ2、σ3为3个方向的主应力；[σ]为许用应力。

在管道所受应力中，径向应力可忽略，式(4)则变为

(5)

2 腐蚀管道强度数值计算

理论公式只能计算完整管道的强度，无法评估腐蚀坑存在产生的应力放大现象，基于理论方法对腐蚀管道的评估不够精确，为未来管道的安全运营埋下隐患，因此有必要开展腐蚀管道的数值分析。

数值分析计算使用有限元软件ANSYS，在进行数值分析之前需要验证数值模型的准确性。首先通过第1节中理论公式反算出各应力下的完整管道承受的内压和轴力，然后在有限元软件中建立完整管道模型(见图4)并加载受力，最后得出数值模型计算的管道应力。计算选取API X65等级钢材，根据材料屈服强度为450 MPa，选取0.1～1.0等10个系数求得应力(即45～450 MPa)，分别反算求出内压和轴力，并单独施加在完整管道模型上，得出数值计算的管道应力。通过对比初始理论应力与数值计算结果得出：内压作用时两者平均误差为2.87%，轴力作用时两者平均误差为1.21%；将内压和轴力同时施加在管道上，两者平均误差为3.31%。由此证明本次计算数值模型的准确性，可进行下一步带腐蚀坑的管道强度数值分析。

图4 完整管道模型

海底管道存在不同几何尺寸的腐蚀，也会出现单腐蚀坑和多腐蚀坑，因此，研究腐蚀坑几何尺寸和腐蚀坑之间间距的应力放大效应有助于认识腐蚀对管道的危害。对单个腐蚀坑和2个腐蚀坑展开数值计算。DNV-RP-F101[4]将不规则形状的腐蚀坑等效成方坑，因此在本次建模中腐蚀坑的形状为长方形，2个腐蚀坑为轴向和周向分布。

2.1 单腐蚀坑强度分析

在ANSYS建模中合理地简化模型，将管道腐蚀简化为长方形。为消除边界效应，根据圣维南原理，模型长度选取3倍管道直径。选用三维8节点六面体Solid 95单元建模，在腐蚀坑及腐蚀坑附近处将网格加密以保证计算精确性，如图5所示。管道的钢材等级为API X65，弹性模量为206 GPa，泊松比为0.3，屈服强度为450 MPa。

图5 单腐蚀坑管道模型

2.1.1 腐蚀坑深度分析

选取管道外径D=0.726 m，管道壁厚t=0.017 5 m，在内压P=15 MPa、轴力F=10 kN条件下建立数值计算模型，腐蚀坑的长度L=0.2 m、宽度c=0.05 m、相对深度d/t=0.1～0.8，计算得出管道最大应力。

图6为管道最大应力随腐蚀坑相对深度变化情况。由图6可知：当腐蚀坑深度d<0.2t时，管道最大应力与腐蚀坑相对深度大致成线性增长趋势；当腐蚀坑深度d=0.2t～0.4t时，腐蚀坑相对深度对管道最大应力的影响不大，且超过材料屈服强度；当腐蚀坑深度d>0.4t时，管道最大应力明显增加，且成非线性增长趋势。

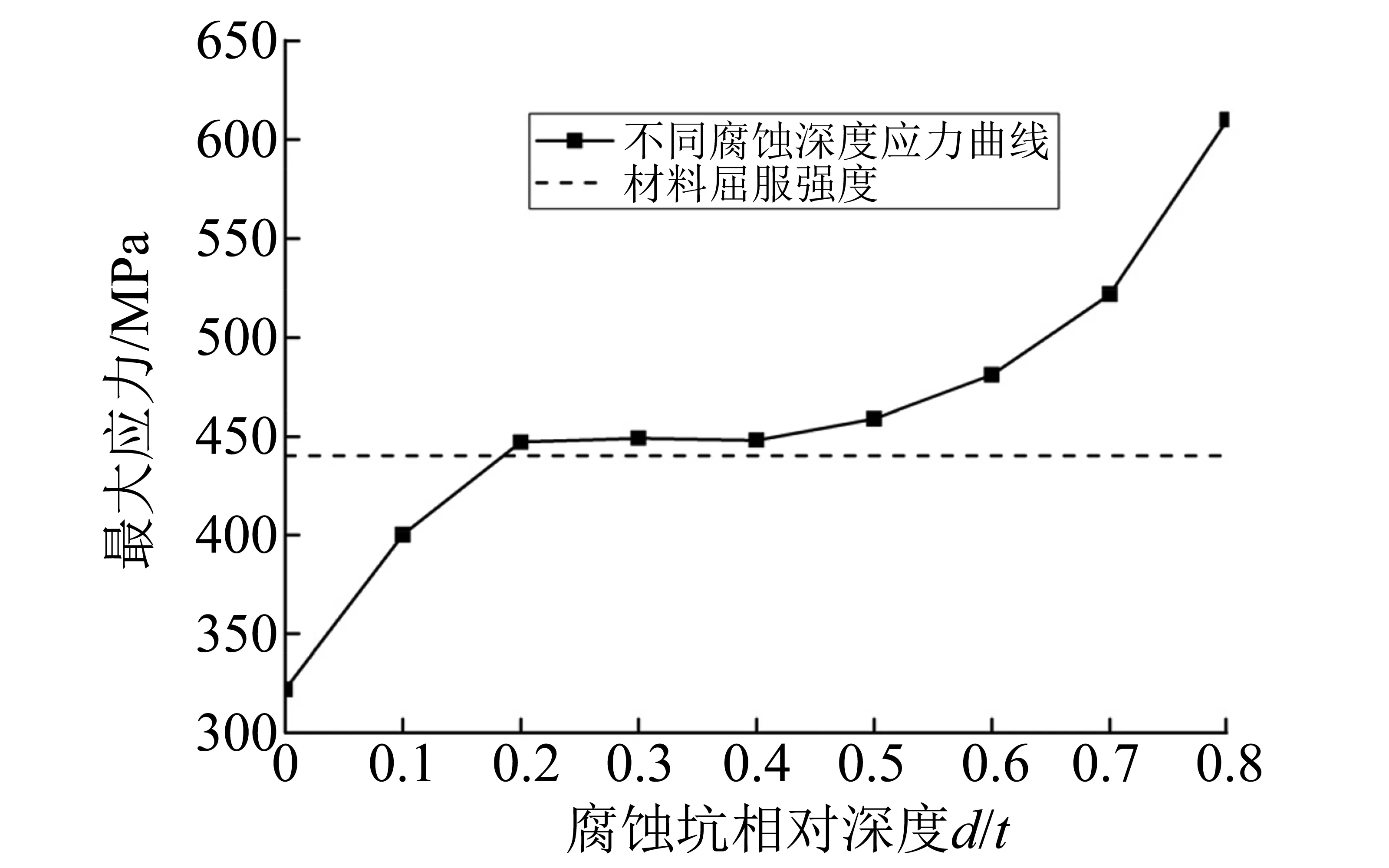
图6 管道最大应力随腐蚀坑相对深度变化

图7为不同相对深度下管道应力分布：在腐蚀坑相对深度较浅时，最大应力出现在腐蚀坑内(见图7(a))；在深度变深后，坑周围的应力变大并接近最大应力(见图7(b))。

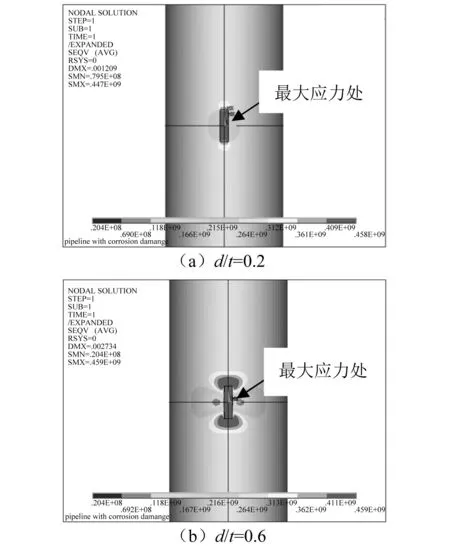
图7 不同相对深度下管道应力分布

2.1.2 腐蚀坑长宽比分析

选取管道外径D=0.726 m，管道壁厚t=0.017 5 m，钢材等级API X65，在内压P=4 MPa、轴力F=2 kN、弯矩M=50 kN·m条件下建立数值计算模型，腐蚀坑长度L=0.2 m、长宽比L/c=1～8、深度d=0.2t，计算得出管道最大应力。应力放大因数为缺陷管道最大应力与完好管道应力比值。

图8为管道应力放大因数随腐蚀坑长宽比变化图。由图8可知：当长宽比L/c<4时，应力放大因数与长宽比成线性增长趋势；当长宽比L/c>4时，应力放大因数受长宽比的影响较小，呈现平稳趋势。由图8也可知腐蚀坑的长宽比越大，也就是腐蚀形状越狭长，应力放大现象越显著，管道越危险。

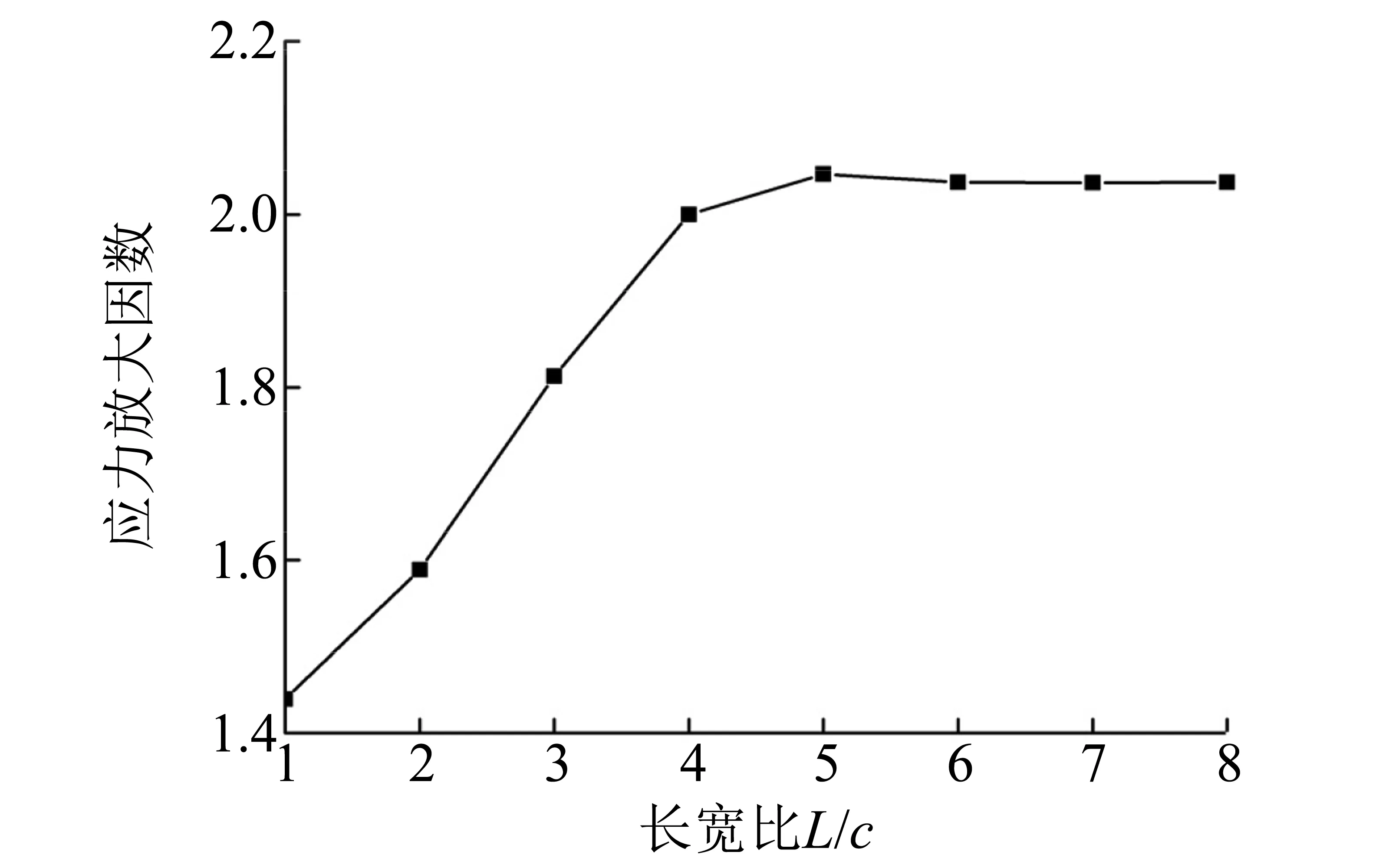
图8 管道应力放大因数随腐蚀坑长宽比变化

2.2 2个腐蚀坑强度分析

在数值计算中将2个腐蚀坑的排列简化为周向和轴向排列，未考虑斜向交错分布的腐蚀损伤。选取管道外径D=0.726 m，管道壁厚t=0.017 5 m，钢材等级为API X65，腐蚀坑长度L=0.2 m、宽度c=0.05 m、深度d=0.5 t，在内压P=4 MPa、轴力F=2 kN、弯矩M=50 kN·m(管道未发生屈服)条件下，在2个腐蚀坑轴向间距g=0.04 m、0.10 m、0.15 m、0.20 m、0.24 m、0.30 m、0.40 m等7种工况下计算得出整个管道最大应力放大因数，如图9所示。由图9可知：应力放大因数与轴向间距的关系为非线性关系，且随着间距增大，应力放大因数成减小趋势；当g≥0.2 m时，应力放大因数趋于稳定。因此，2个腐蚀坑间距越大，应力放大因数越小，当间距超过一定值时，可忽略腐蚀坑之间的相互影响。

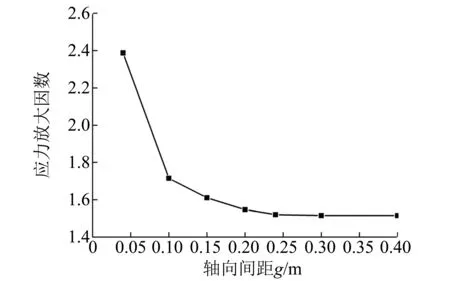
图9 管道应力放大因数随轴向间距变化

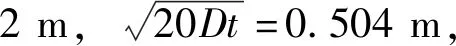
表1 腐蚀坑间距相互作用准则

随后对该管道在内压P=15 MPa、轴力F=10 kN载荷下(发生屈服时)进行计算，根据2个腐蚀坑轴向和周向间距4种不同工况，得到腐蚀坑损伤计算结果，如表2所示。

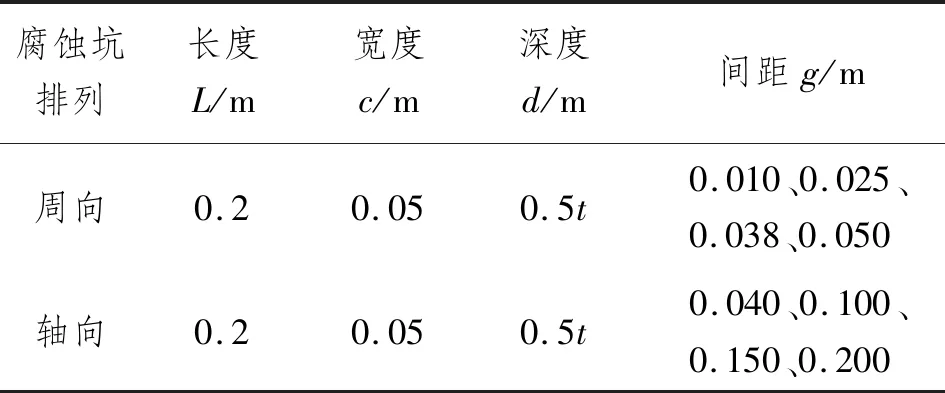
表2 2个腐蚀坑工况

图10为2个腐蚀坑条件下最大应力变化图。

由图10可知：在轴向间距g=0.04 m和周向间距g=0.01 m时，腐蚀管道最大应力大于单腐蚀坑时最大应力，即2个腐蚀坑间互相影响；当间距继续增大时，腐蚀管道的最大应力与单腐蚀坑的几乎一致，即2个腐蚀坑不会产生相互影响。为了与单腐蚀坑应力分布图作对比，给出轴向分布时管道应力分布图(见图11)，通过与图7(b)对比，可以看出当轴向间距较小时，最大应力位于靠近2个腐蚀坑对称轴一侧，轴向间距越大，2个腐蚀坑应力分布越接近于单腐蚀坑。鉴于周向与轴向结论相似，不再对周向2个腐蚀坑的应力分布进行描述。

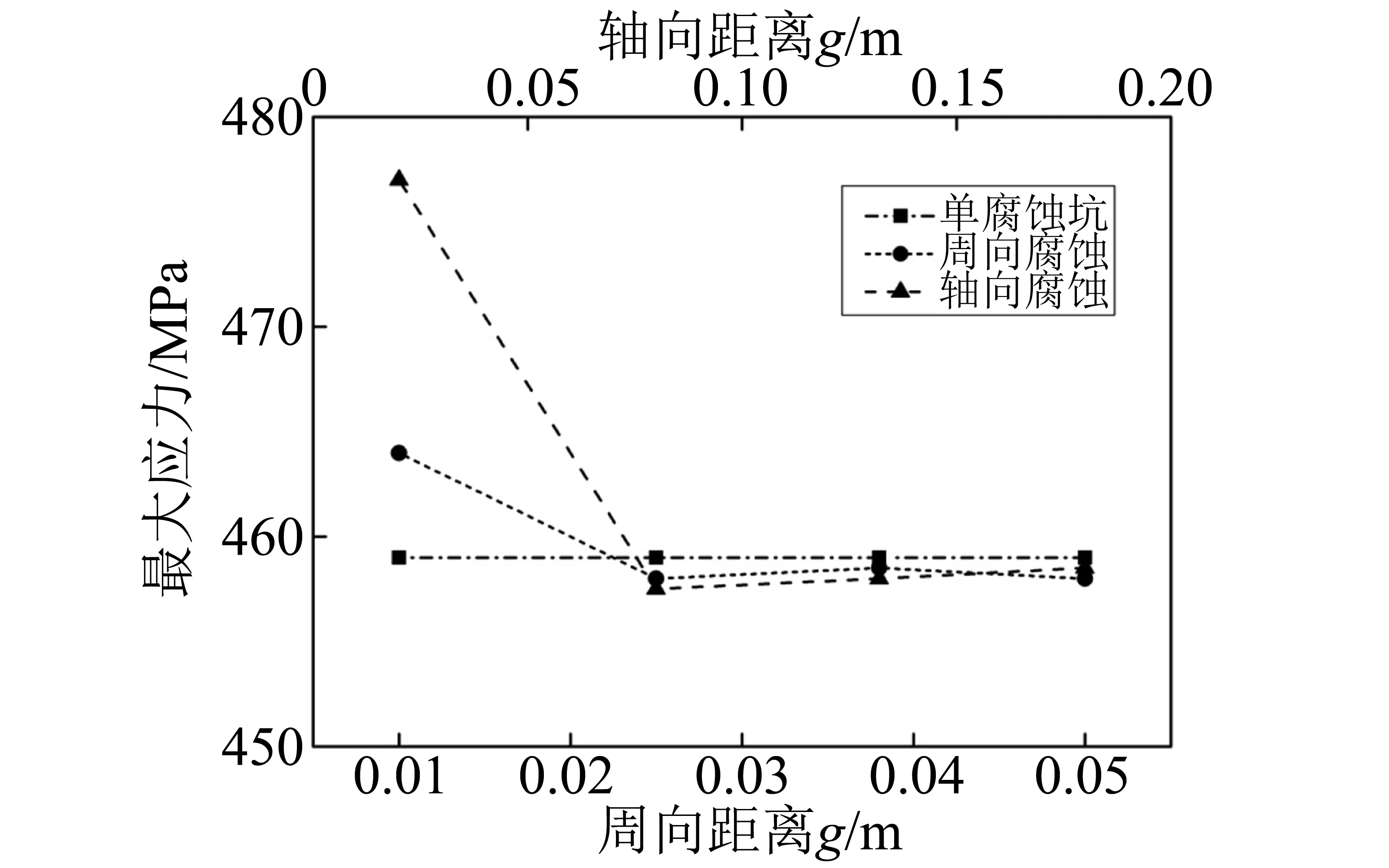
图10 2个腐蚀坑条件下最大应力变化

图11 轴向分布时不同间距下管道应力分布

AL-OWAISI等[24]利用有限元软件对带有不同形状相邻缺陷的管道进行分析，发现两种形状(椭圆形和矩形)的相邻缺陷在轴向距离不大于3.0t或周向距离不大于0.5t时均会产生相互作用。在上述算例中轴向间距g>0.04 m/周向间距g>0.01 m时，即轴向间距g>2.286t/周向间距g>0.571t，2个腐蚀坑相互作用，与文献结论基本一致。

对比轴向/周向2个腐蚀坑结论也可发现，管道发生屈服前的轴向临界间距为(g)Lim=0.20 m，而发生屈服后的临界间距则为(g)Lim=0.04 m，因此管道发生屈服前的临界间距大于管道发生屈服后的临界间距。

3 已建海管强度校核

选取我国浅海海域某条海管为算例，对比均匀腐蚀下与局部腐蚀下的计算结果。管道外径D=0.323 9 m，壁厚t=0.012 7 m，钢材等级API X65，设计压力为12.7 MPa，设计温度为80 ℃。载荷条件为内压P=13.06 MPa、轴力F=713 kN、弯矩M=96.78 kN·m。

假设该管道带有不同程度的腐蚀损伤(见表3)，则强度计算结果对比如表4所示。

表3 腐蚀损伤工况

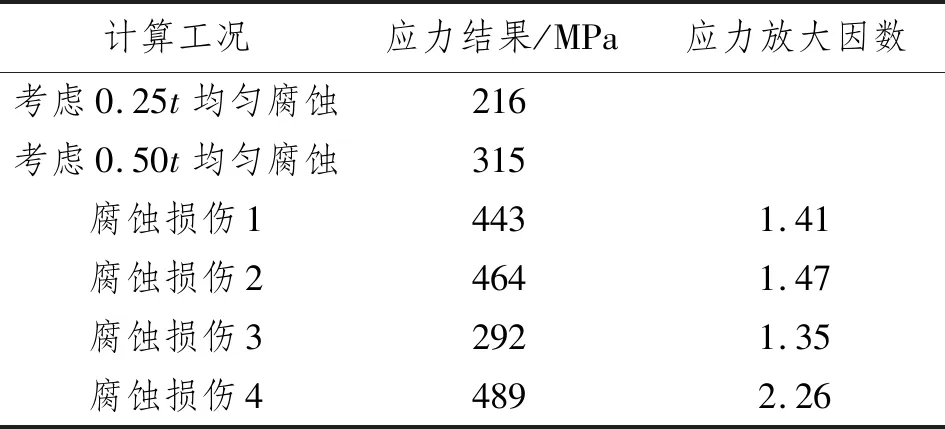
表4 不同工况下管道腐蚀计算结果

由表4可知：在仅考虑0.25t均匀腐蚀裕量时，管道所受应力为216 MPa；在考虑0.50t均匀腐蚀裕量时，管道所受应力为315 MPa；在考虑实际腐蚀损伤数值计算结果中，最大应力达489 MPa，应力放大因数为2.26。因此，在对带腐蚀海管强度进行校核时，仅考虑管壁的均匀腐蚀是不够的，还需考虑管道腐蚀造成的应力集中现象。在实际工程项目中，应针对腐蚀超过设计裕量的区域开展剩余寿命评估，判断其是否满足海管服役期的完整性要求，对不满足要求的区段进行及时治理或更换。

4 结论与展望

基于ANSYS有限元方法分析单腐蚀坑、2个腐蚀坑条件下管道应力，2个腐蚀坑为轴向和周向分布，将计算结果与LI等和AL-OWAISI等数值模拟结论进行对比，同时对浅海海域某海管进行强度校核，得出主要结论如下：

(1) 对于单腐蚀坑，腐蚀深度是最关键的因素，腐蚀越深，长宽比越大，腐蚀造成的应力放大现象越明显。

(2) 2个腐蚀坑间距增大，应力放大因数逐渐变小，当超过临界间距时，可忽略腐蚀坑之间的相互影响。管道发生屈服之前的临界间距大于管道发生屈服之后的数值。

(3) 在对已建海管进行强度校核时，仅考虑管道的均匀腐蚀不够准确，还应考虑腐蚀产生的应力集中现象。

将腐蚀损伤形状简化为长方形，2个腐蚀坑为轴向和周向并列分布，管道所受载荷仅考虑内压、热膨胀和悬跨状态下的受力。实际上，腐蚀损伤形状不规则且常以群落方式出现，且管道处在海底所受载荷复杂，为得到更加准确的评价结果，未来需针对在多种载荷作用下存在不规则腐蚀群落的管道进行腐蚀评估。