基于深度置信网络的煤层含气量测井解释研究

胡 驰，李新虎,2,3*，李晓君，李 健，郭 杰

(1.西安科技大学地质与环境学院, 西安 710054；2.陕西省煤炭绿色开发地质保障重点实验室，西安 710054；3.国土资源部煤炭资源勘查与综合利用重点实验室，西安 710021；4.甘肃煤炭地质勘查院，兰州 730000)

煤层气的开发过程中，煤层含气量的解释和评价对生产至关重要。目前，确定煤层含气量最准确的方法就是现场取心后实验室解吸。这种方法成本较高，因此，煤层气开发需要一种经济、有效且通用的煤层气含量解释方法。

目前有学者利用地球物理测井资料预测煤层含气量，主要方法有概率统计法[1-2]、等温吸附曲线法[3-4]和BP神经网络[5-6]。但是，基于多元线性回归所建立的概率统计法，对于计算煤层含气量这种非线性问题，仍存在较大误差。Langmuir方程的计算结果会受到甲烷饱和度的影响，且大多数情况下，煤层气属于欠饱和吸附[7]，因此，计算结果仅为煤层中的相对煤层气含量。BP神经网络虽然可以解决非线性的复杂问题，但由于初始值的随机性，导致计算过程中容易陷入局部最小值或产生过拟合问题[8]。深度学习可以有效的发现并描述问题的复杂结构[9-10]，其在很多领域获得了成功[11-15]，但目前很少应用到测井解释。

笔者在本次研究中，将深度学习的深度置信网络(DBN)引入到煤层含气量预测中，结合合水地区测井数据，确定了可用来计算合水地区煤层含气量的DBN网络参数，构建了DBN网络，该方法可用来对合水地区煤层气测井数据进行定量解释。

1 研究区概况

合水地区位于陕北单斜的西南部，总体呈向NW倾斜的复式单斜构造，倾角平缓，一般在3°～10°。区内褶曲发育平缓，轴线走向多为NEE—SEE，延伸长度平均11.35 km，褶曲形态宽缓，轴线也呈不连续的波状起伏，起伏幅度总体由下层段向上层段到盖层呈逐渐变小的趋势；排列方向不一，形态略显鼻状、簸箕状，或穹窿、或凹陷的特征。研究区含煤地层为中侏罗统延安组，含煤1～14层，有编号煤层5层。其中，5号煤全区可采，平均厚度分别为2.18 m，埋深大于880 m；6号煤和8号煤层局部可采，平均厚度为2.03 m和2.96 m，埋深大于965 m。由于研究区内8号煤气含量最高，故本次以合水地区8号煤煤层含气量为研究对象(图1)。

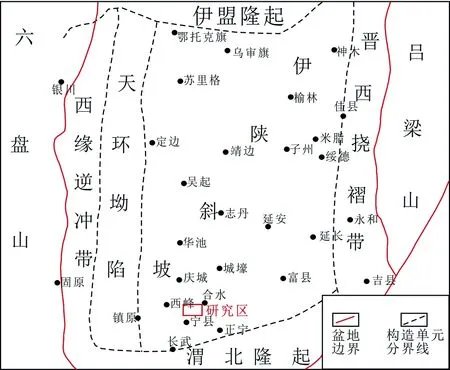
图1 鄂尔多斯盆地构造及研究区位置图Figure 1 Structural map of Ordos Basin and study area position

2 深度置信网络

深度学习的提出，不仅起源于对人工神经网络的研究，还受到统计力学的启发[16-17]。在此基础上，Hinton等在2006年提出了深度置信网络[18]，该方法结合了无监督和监督学习，其中涉及多个受限的玻尔兹曼机(RBM)和BPNN[19]。

2.1 受限玻尔兹曼机(RBM)

RBM是DBN中无监督学习的最重要部分，其包含两层：一层是可视层，用于接收输入，另一层是隐藏层。每层由许多神经元组成，用于提取输入参数特征(图2)。同一层中的神经元彼此独立，各个可视层和隐藏层神经元通过权重矩阵V连接，其可以表示为

(1)

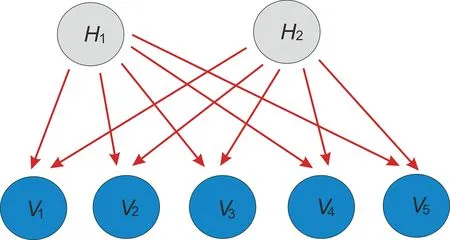
图2 RBM网络结构Figure 2 RBM network structure

式中：i表示可视层神经元数量；j表示隐藏层神经元数量，通过权重矩阵V选择打开或者关闭神经元，(用1和0分别表示神经元打开和关闭)。

当输入向量为X=(X1，X2…Xn)T，首先需要计算隐藏层中神经元的激励值：

Y=VX

(2)

此时，Y=(Y1，Y2…Yn)T，通过Sigmoid函数计算隐藏神经元被打开的概率：

(3)

Ym=1表示隐藏神经元打开。故隐藏层神经元被关闭的概率为

P(Ym=0)=1-P(Ym=1)

(4)

最后通过比较均匀分布的随机值h(h∈[0,1]),来确定隐藏层神经元是否会被打开：

(5)

式中：Ym∈Y。

RBM的训练实质上就是通过选择神经元的打开或关闭，来建立可反映样本特征的概率分布。

2.2 反向传播神经网络(BPNN)

BPNN由Rumelhart和McClelland于1986年提出，是一种基于反向传播算法的多层前馈神经网络[20]。BPNN是DBN中监督学习的一部分，主要用于计算最终输出。BPNN可以分为三层：输入层(I)、隐藏层(h)和输出层(O)，仅含有一层输入层和一层输出层，但可能会有一层或几层隐藏层(图3)。在每一层中都有许多神经元，同一层中的神经元彼此不连接，前后两层的神经元通过权重w连接。输入层接收数据，隐藏层和输出层处理数据。数据处理通常使用Sigmoid函数：

(6)

(7)

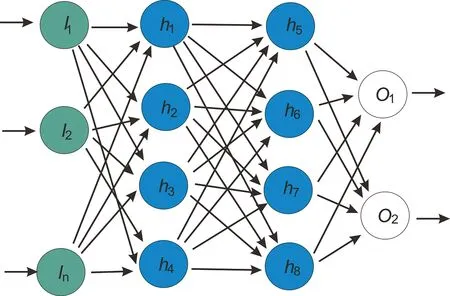
图3 BPNN网络结构Figure 3 BPNN network structure

式中：yi表示i层的输入；xi表示前一层输出；wi表示前一层权重；b表示调节系数；yo表示i层的输出。

3 深度置信网络结构

将RBM提取的测井曲线参数特征用作BPNN的新输入，从而对DBN进行训练。单个BPNN是典型的“浅”层神经网络。当隐藏层大于2时，计算结果不理想。但在DBN中，可以通过多层RBM提取参数特征，DBN通过RBM确定连接权重W的范围，然后通过BPNN训练计算结果(图4)。与单BPNN相比，DBN的训练速度和收敛时间更快，且精度更高。

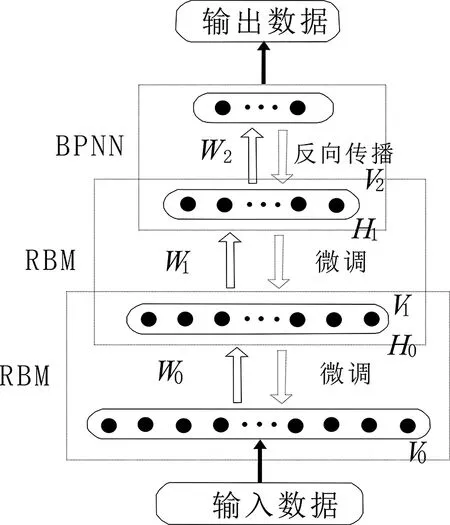
图4 DBN网络结构Figure 4 DBN network structure

3.1 归一化数据

不同的测井曲线的技术原理和物理参数存在明显差异。因此必须对测井数据进行预处理，将其统一到相同的尺度范围内。

(8)

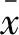
含气量对不同测井曲线的影响各不相同，故需要分析不同测井曲线与含气量之间的相关性。选择合水地区，井径、自然伽马、自然电位、密度、声波时差、短源距伽马测井、长源距伽马测井和浅侧向8条测井数据，通过灰色关联分析方法，来分析二者之间的相关性。

(9)

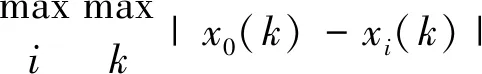
表1为合水地区测井数据与煤层含气量之间的相关性，关联度越大，说明其相关性越高。本文选择关联度大于0.8的测井曲线，分别为：短源距自然伽马、自然伽马、密度、长源距自然伽马和浅侧向5条测井曲线，作为后续DBN训练的输入参数。

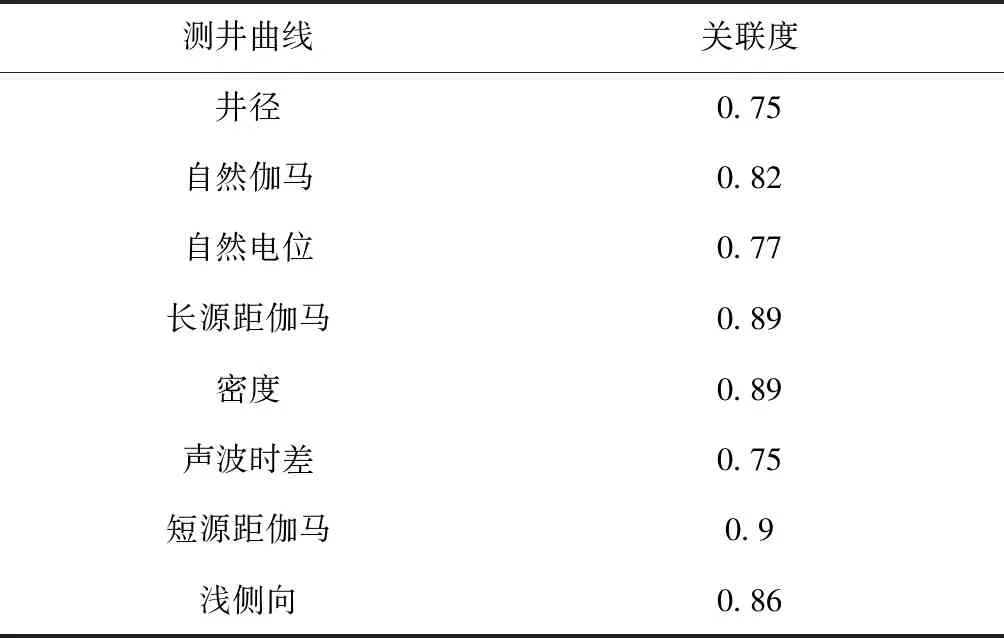
表1 测井数据和煤层含气量灰色关联排序

3.2 RBM层数影响

本次研究以甘肃合水地区测井数据为例，筛选出该地区120组煤层样品作为DBN样本分析数据。选择短源距自然伽马、自然伽马、密度、长源距自然伽马和浅侧向5条测井曲线，作为DBN的输入参数，煤层气含量作为DBN的输出参数。分别研究RBM数量和隐藏神经元数量对计算结果的影响。最后通过概率统计法、BPNN、DBN和SVM计算了30组煤层的煤层气含量，并分析了不同方法的效果。

DBN通常由多组RBM和一组BPNN组成。RBM主要用于对测井参数特征的提取，其数量对计算结果有一定的影响。一般来说，RBM层数越多，提取的参数特征越有效，计算结果更加准确。但相应的计算速度会下降。因此，要同时考虑到计算结果的准确性和计算速度。

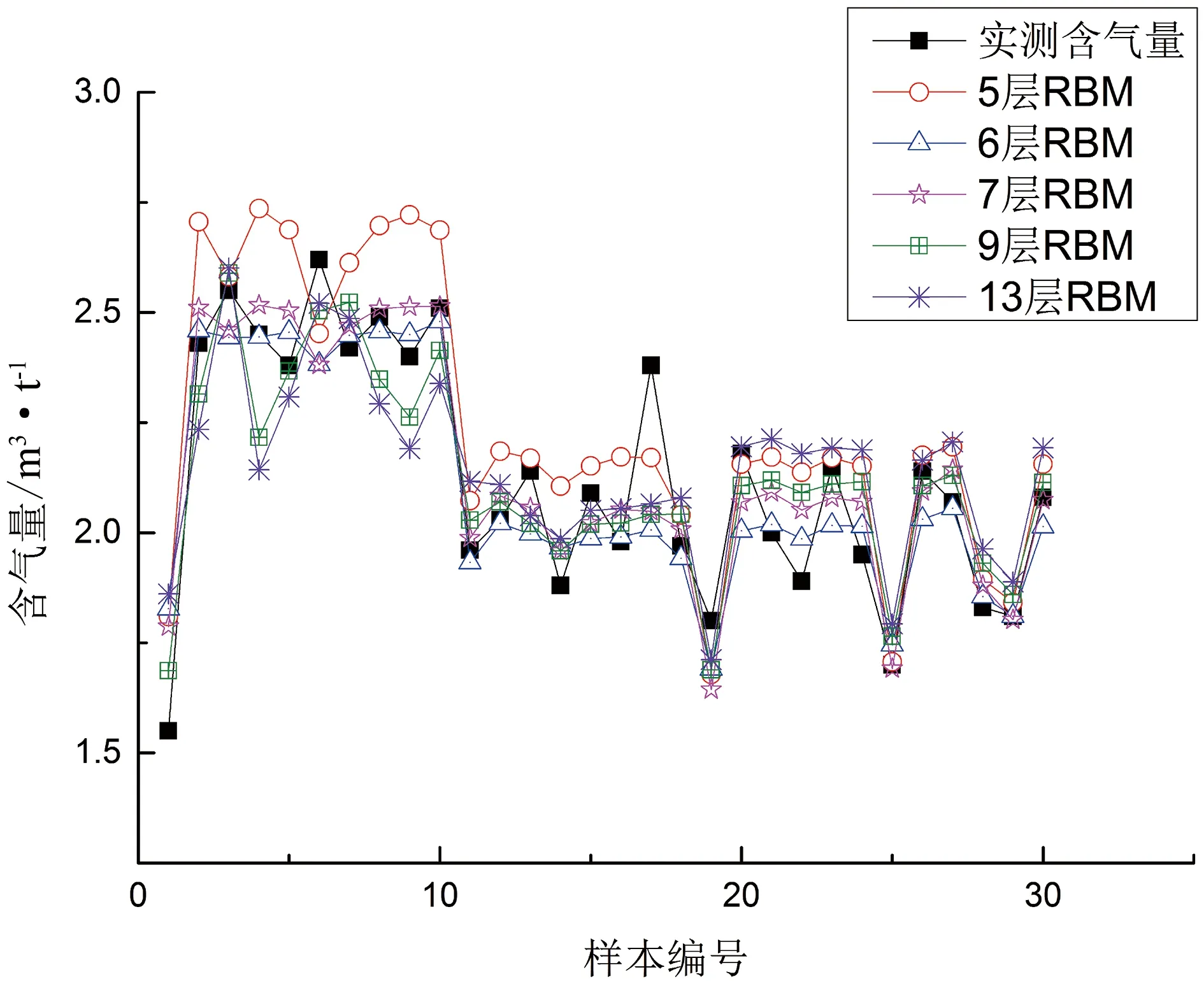
图5 不同RBM层数计算结果对比Figure 5 Comparison of different RBM layer numbers computed results

随着RBM层数由5层提高到7层，计算结果与实验室分析结果之间的差异性随之降低。但RBM层数增加到9层及以上时，计算精度并没有显著提高，反而由于操作复杂，导致计算速度明显降低(图5)。因此，在本研究中，选择计算结果精度更高，计算速度适中的7层RBM，作为隐藏层的层数。

3.3 神经元数量的影响

每个RBM由可视层和隐藏层组成。可视层主要用于接收测井参数，其神经元数量与输入测井参数数量相同，为5个。隐藏层主要用于提取测井曲线特征，其神经元数量对测井曲线特征的有效提取存在很大影响。故本次选择5、10、20和50个神经元作为实验对象。

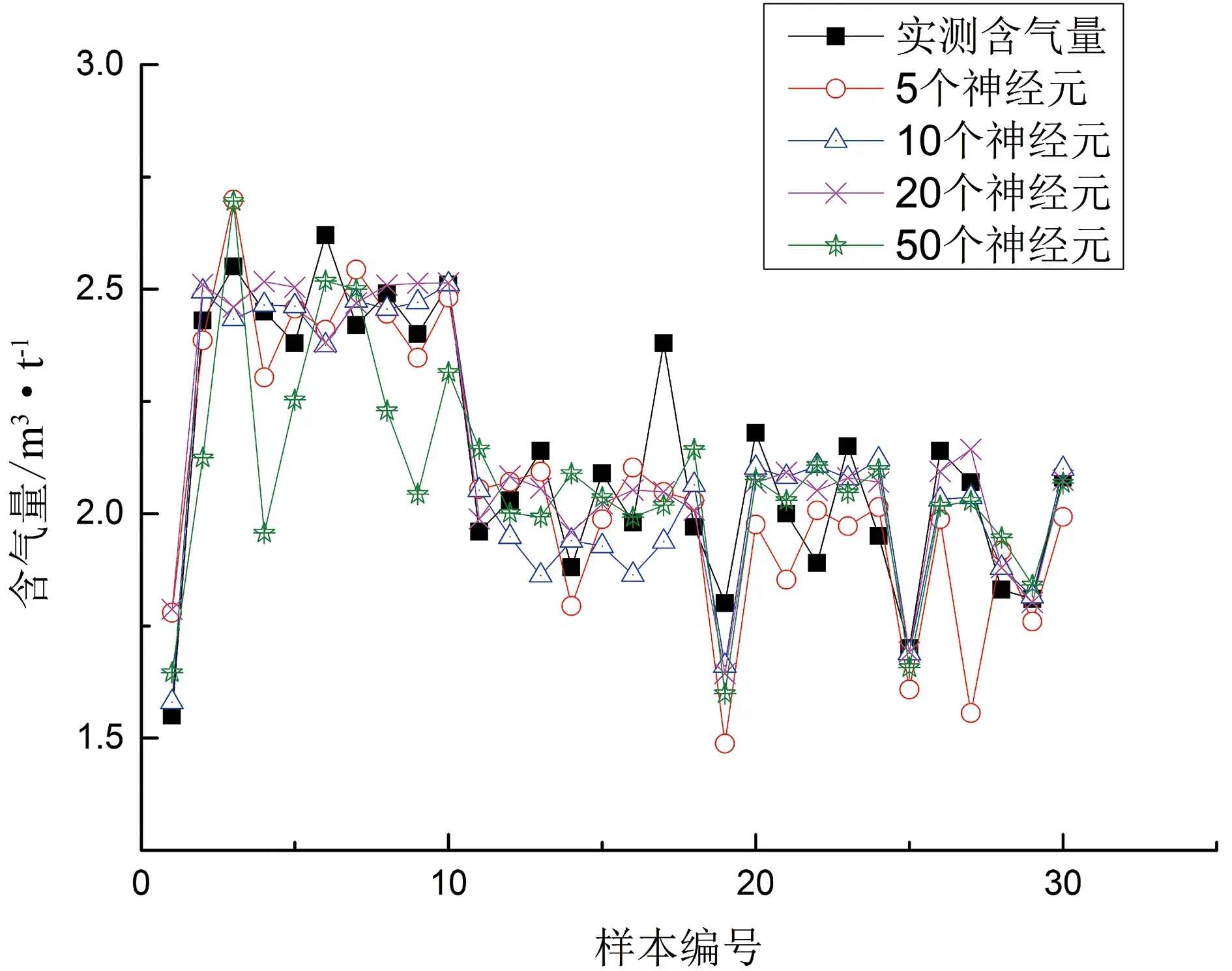
图6 不同神经元计算结果对比Figure 6 Comparison of different neurons computed results

当存在50个神经元时，计算结果与实验室分析结果差异最大，且耗时最长，说明过多的神经元并不能更好的改善计算精度。当有5个神经元时，计算结果的精度明显高于50个神经元，但由于神经元数量过少，可能无法提供最有效数据特征，导致最终的计算结果不稳定，因此需要重复计算来提供最佳输出结果。当神经元数量为20时，计算结果与实验室分析结果差异更小且结果稳定(图6)。故在后续训练中，将20个神经元作为每个RBM隐藏层中的最佳神经元数量。

4 相关预测方法比较

4.1 概率统计法

概率统计法一般假设煤层气含量与测井数据之间存在一定概率分布关系[21]，因此，可通过多元回归方法，获得煤层气含量和测井数据之间的回归方程。通常，概率统计法可用来预测同一区域中的煤层气含量，但是其误差较大，计算结果精度偏低。

为了寻找最优的含气量测井解释模型方程，对合水地区煤层气参数井的煤层样品测试含气量和测井数据进行多元回归，发现含气量与各测井参数之间在多元回归的情况下有一定的相关关系，其计算公式：

Gas=-0.05992*DEN+0.000247*GGNR+0.000283*GGFR-0.0002*GR-0.00017*LL3+0.905329

(10)

R2=0.64

F=40

式中：R2为相关系数平方；F为统计量；Gas为含气量，m3/t；DEN为密度测井曲线,g/cm3；GGNR为短源距伽马测井曲线，API；GGFR为长源距伽马测井曲线，API；GR为伽马测井曲线，API；LL3为浅侧向测井曲线,Ω·m。

整体样本预测效果较好(表2，图7)，虽部分样本相对误差达到20.16%，但整体样本相对误差较小，平均为11.18%。给定显著性水平α=0.05，测试样本数量M=120，自变量n=5，查阅F检验临界值表可知，F0.05(5，114)=2.294，F=40>F0.05(5，114)=2.294，多元回归关系成立。R2=0.64，含气量与5个测井参数之间关系显著，模型具有较高可信度，若没有其它计算含气量方法时，可优先考虑该方法。

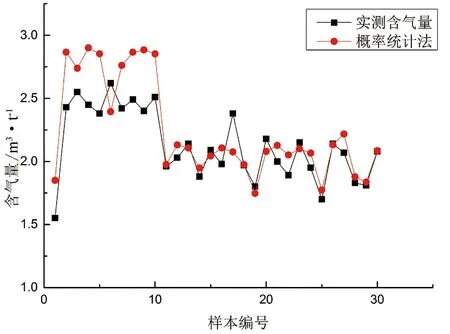
图7 合水地区概率统计法预测含气量结果Figure 7 Probabilistic method predicted gas content results in Heshui area

4.2 SVM

SVM在解决小样本、非线性等回归问题中表现出许多特有的优势，基于统计学习理论中结构最小化原则和VC维理论，在保证精度的同时降低学习机器的VC维，进而控制学习机器在整个样本集上的期望风险，以期得到最小误差[22]。

通过密度、短源距伽马、长源距伽马、伽马和浅侧向5条测井曲线，对煤储层含气量进行预测。使用合水地区120组数据分析训练，建立支持向量机含气量预测模型，并对剩余30组样本进行预测分析。

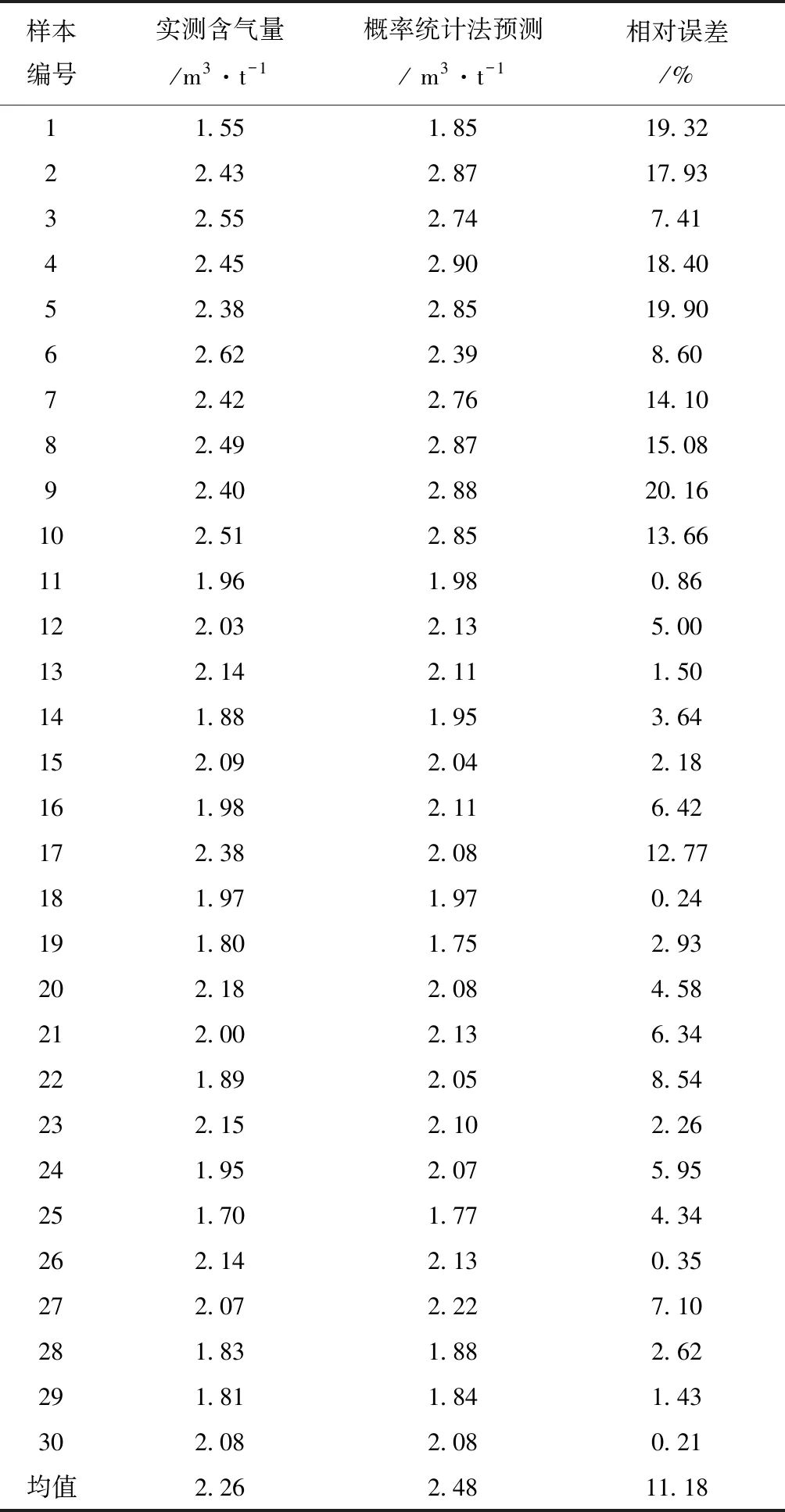
表2 合水地区概率统计法预测结果

整体样本预测效果较差(表3，图8)，即使部分样本预测精度较高，相对误差仅为2.87%，但仍有部分样本相对误差结果达到51.39%，而整体平均相对误差为25.32%。SVM本质上是非线性方法，当样本数量比较少时，网络模型更容易抓住样本和特征之间的非线性关系；而样本数据较大时，会导致该矩阵的存储和计算将会耗费更大的机器内存和运算时间，且不利于关键样本的抓取，进而使得网络模型预测结果精度较低。

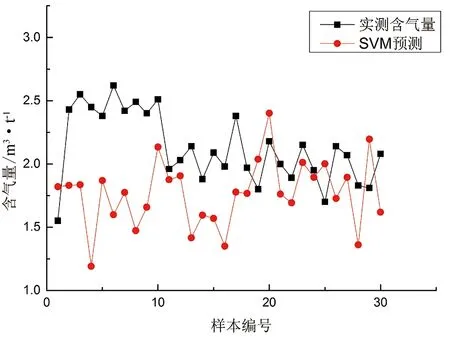
图8 合水地区支持向量机预测含气量结果Figure 8 SVM predicted gas content results in Heshui area

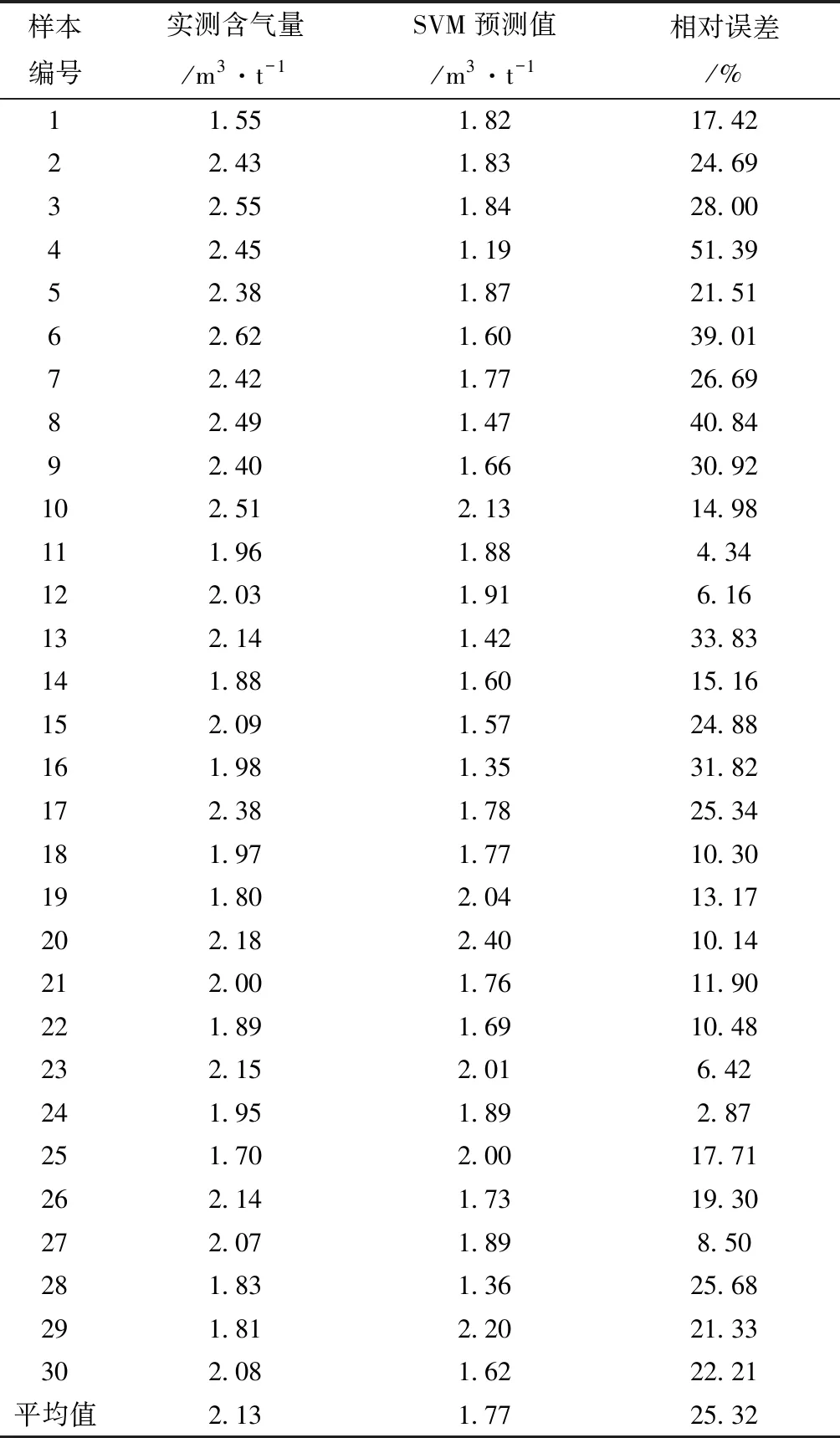
表3 合水地区支持向量机预测结果

4.3 BPNN

BP网络具有逼近任何非线性映射的能力，可以不受非线性模型的限制，并且学习算法简单，建模方式灵活等特点,对已知存在某种联系但无法用确切方程或算法表达的求解问题有更高的适用性[3，23]。

本次选择密度、短源距伽马、长源距伽马、伽马和浅侧向5条测井曲线作为输入函数，煤层含气量为输出函数，隐含层节点数为7，构建BP神经网络模型。

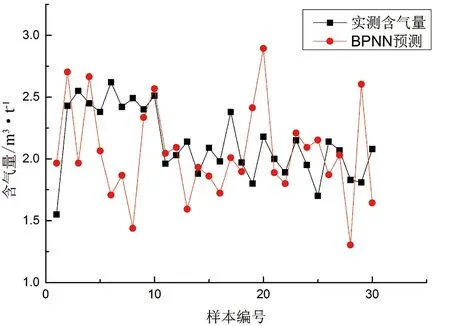
图9 合水地区BPNN预测含气量结果Figure 9 BPNN predicted gas content results in Heshui area

BPNN预测结果精度略高于SVM(表4，图9)相对误差分布在1.92%～43.86%，平均相对误差为15.64%。一般情况下，随着训练能力的提升，预测能力的精度也随着提高。但这种趋势存在一个极限，当训练能力不断提高，网络模型学习到的样本特征细节就越多，此时模型已不能反映样本特征的规律，使得网络预测能力下降。故如何把握学习能力的度，对BPNN预测精度的准确性存在很大影响。

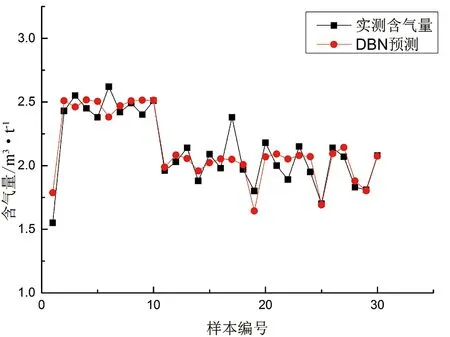
图10 合水地区DBN预测含气量结果Figure 10 DBN predicted gas content results in Heshui area

DBN由7个RBM和一个BPNN组成，每个RBM包含20个神经元，通过使用激活函数来给神经元引入非线性因素，使得神经网络可以逼近任何的非线性函数，从而可以让模型的计算结果精度提高，更有效的解决非线性问题。相比其它激活函数，ReLU函数收敛速度更快，计算复杂度更低，故本次研究使用ReLU作为激活函数。通过损失函数均方误差(MSE)反映计算结果与期望之间的差异。

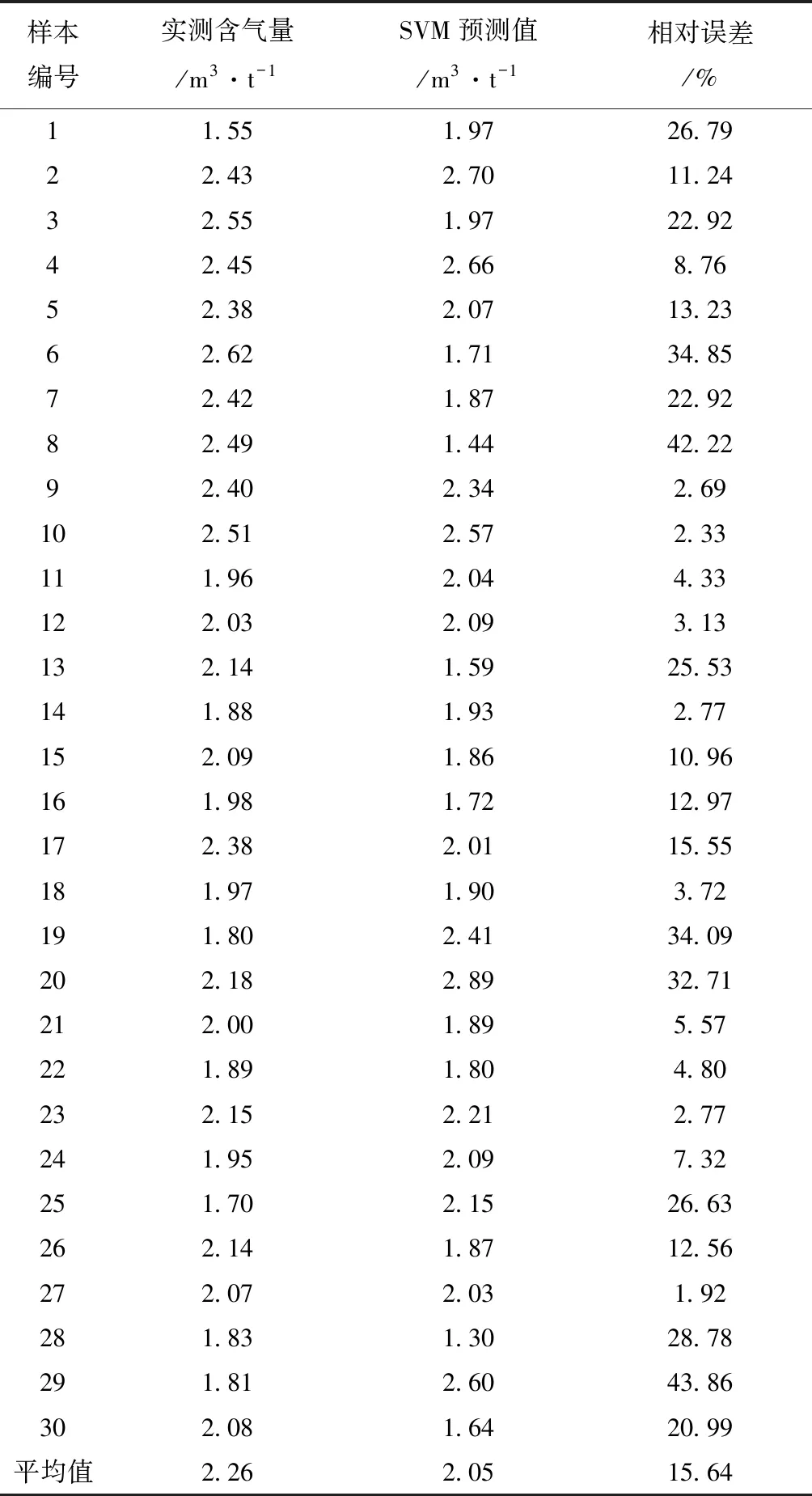
表4 合水地区BPNN预测结果

不同预测方法均方误差(MSE)结果如表5、图10、图11)。由此可见，最准确的方法是DBN，其均方误差分布在0～0.11，平均为0.013，测试含气量与计算含气量匹配度较高。通过密度、短源距自然伽马、长源距自然伽马、伽马和浅侧向测井五条曲线所构建的DBN网络，对合水地区煤层含气量预测有很高的准确性。概率统计法准确度次于DBN，其均方误差分布在0～0.234，平均值为0.054。准确度最差的是SVM，均方误差分布范围较大，平均值为0.293。DBN的精度明显高于BPNN，DBN和BPNN之间的区别在于DBN存在多个RBM，进而通过逐步确定连接权重来构建DBN学习网络，而BPNN的连接权重是随机初始化的。对于DBN来说，通过RBM确定连接权重范围至关重要，可以有效提高计算结果精度。概率统计法与DBN基本相似，都是通过煤层气含量与测井数据之间关系，来估算其它煤层中的煤层含气量。两种方法的差异在于概率统计法通常表示为线性回归方程，而对于煤层含气量这种非线性问题，通过DBN所提供的神经网络得到的结果，往往会有更高的准确度。

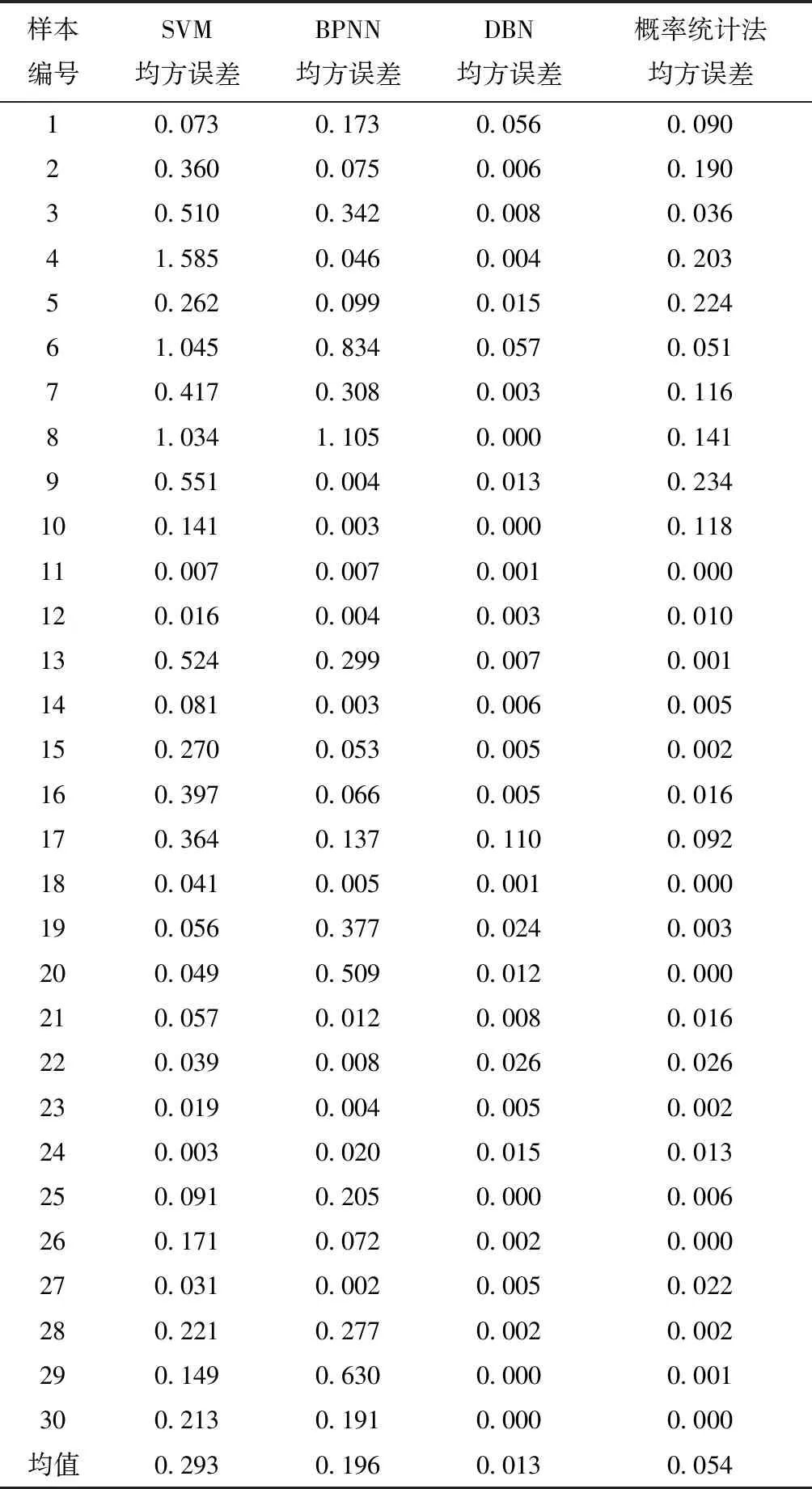
表5 不同预测方法均方误差(MSE)结果对比

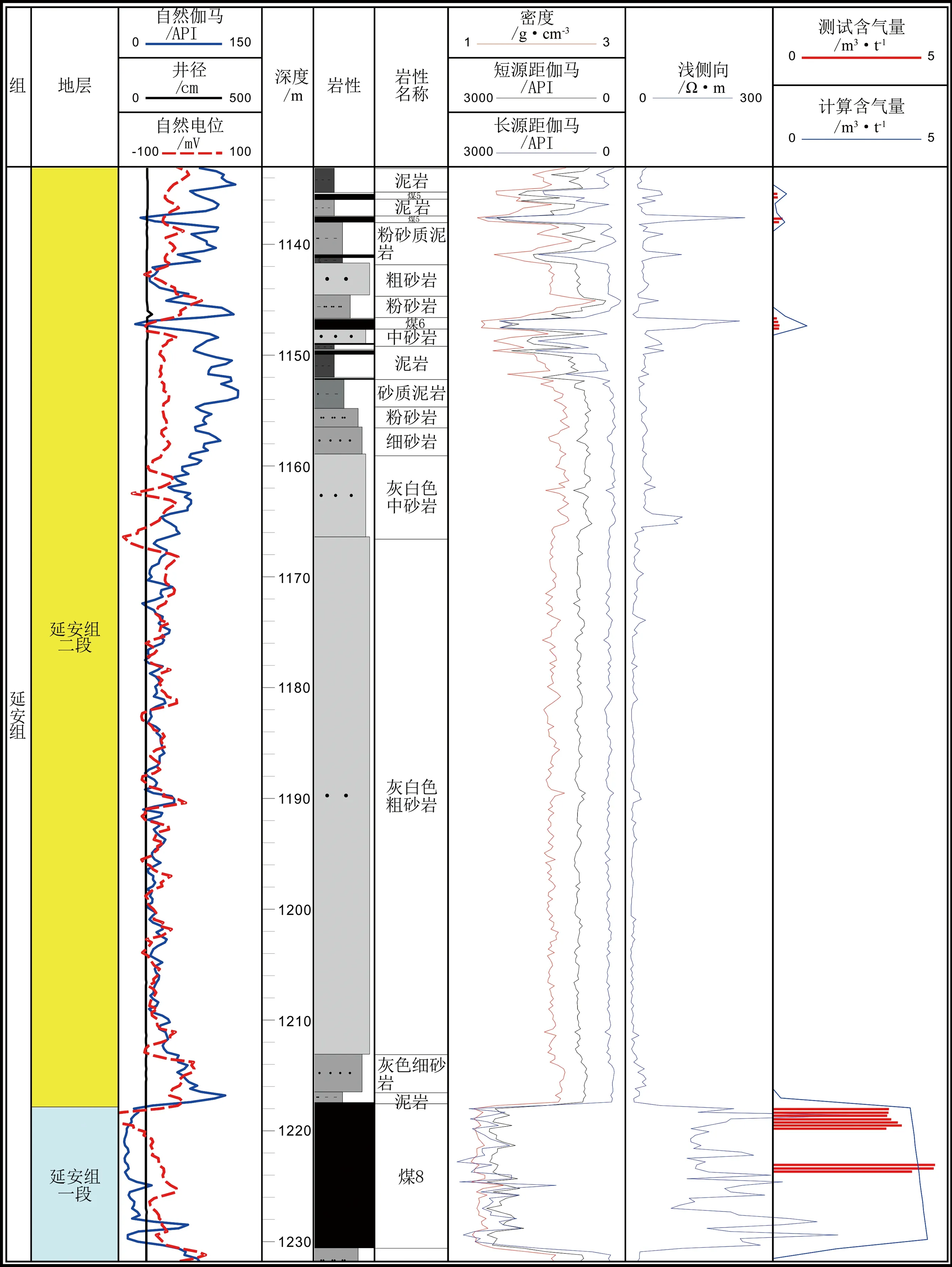
图11 合水地区A井煤层含气量综合预测Figure 11 Well A coal seam gas content integrated prediction in Heshui area

5 结论

1) 增加RBM数量，一定范围内有助于提取测井数据的特征，但是运算速度明显增加，耗时增加。因此，RBM数量并不是越多越好，在考虑结果精度的同时，还需要考虑运算速度，本次研究中RBM层数最优层数为7层。

2) 过多RBM隐藏层神经元会降低计算精度，且增加运算速度，而过少隐藏层神经元虽然会减少运算速度，但会降低结果稳定性。因此，需要反复试验，从而确定适合研究区数据隐性层神经元的数量，本次研究选择神经元数量最优为20。

3) 本次对比研究合水地区煤层含气量预测方法中，DBN预测效果最好，概率统计法次之，SVM效果最差。