钢桁架桥技术状况评定体系中的部件权重分析

童 浩，杨 羿，李程焕，刘 朵,，张建东

(1.江苏宁沪高速公路股份有限公司，南京 210049； 2.苏交科集团股份有限公司，南京 211112；3.河海大学，南京 210098)

随着钢结构桥梁的推广应用及现有钢桥使用年限的增加，其病害问题日益严重[1-4]。为此，需对在役钢桥的技术状况进行准确评定，以便系统地掌握桥梁使用功能与承载能力，为桥梁养护决策提供可靠依据[5-6]。现有公路桥梁技术状况评定主要依据JTG/T H21—2011《公路桥梁技术状况评定标准》[7]，采用了“构件-部件-部位-桥梁总体技术状况”的评定流程[8]。但在钢桥运营养护过程中逐渐反映出部件权重划分不明，养护工程师难以评定的问题[9-10]。

目前，桥梁技术状况评定过程中的部件权重值体系主要由专家打分确定[11-12]。但是，该方法需要大量收集业内专家意见，并且专家判断有时差异很大，影响计算得到的部件权重值的可信度。广义贴近度综合评判法是一种基于模糊数学的具体应用方法。郭晓媛[12]基于贴近度理论对加固后桥梁进行了技术状况评定；王琦[13]通过模拟结构损伤求解了钢桁架系杆拱桥3个主要承重构件的相对权重，解决了评定主观性与算法确定性的矛盾。

本文基于某实际钢桁架桥有限元模型，采用刚度折减模拟部件损伤，研究各个部件不同损伤工况下自振频率与屈曲特征值的变化，基于广义贴近度原理提出了一套钢桁架桥部件权重计算方法。

1 工程概况

某单跨下承式简支钢桁架桥，全长88 m，主桁采用带竖杆的华伦式三角形腹杆体系，节间长度8 m，主桁高度11 m，桥面车道行车宽度19.25 m。上、下平面纵向联结系均采用双X形式，与弦杆在节点处相连。钢桁架桥型布置如图1所示，其部件分类如图2所示。

单位：mm

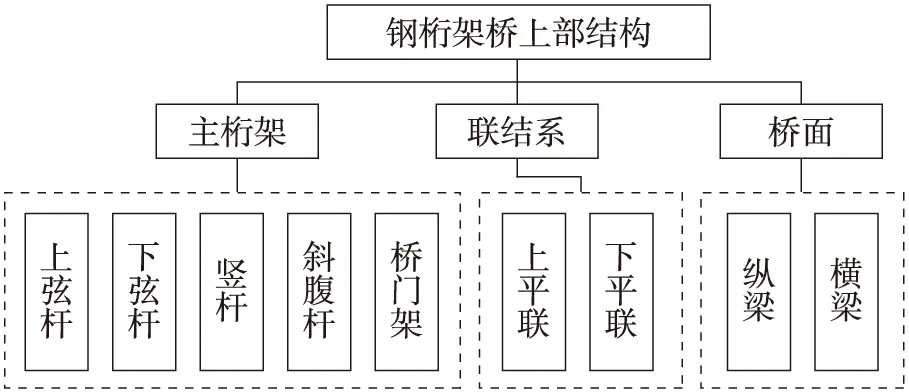
图2 钢桁架桥部件分类

2 计算模型

采用Midas/Civil有限元分析软件建立钢桁架桥整体分析模型，如图3所示。主桁架、联结系、桥面纵横梁均采用梁单元模拟，材料采用Q370qD桥梁用低合金结构钢，弹性模量为2.06×105MPa。在端横梁与下弦杆连接节点设置简支边界条件，按照JTG D60—2015《公路桥涵设计通用规范》分别施加桥梁自重、桥面铺装荷载与车辆荷载。

图3 钢桁架桥有限元分析模型

3 部件权重分析

3.1 分析思路

钢桁架杆件一旦损伤，一是会造成截面削弱，带来杆件屈曲风险；二是因杆件刚度的降低，会影响桥梁振动特性。因此，对于钢桁架部件权重的划分不能简单地由单一因素控制，而应考虑多种因素的影响。本文采用刚度折减模拟部件损伤，通过结构前10阶自振频率与屈曲特征值的变化，综合评价钢桁架每类部件的相对重要性程度，从而制定钢桁架部件权重。部件权重分析流程如图4所示。

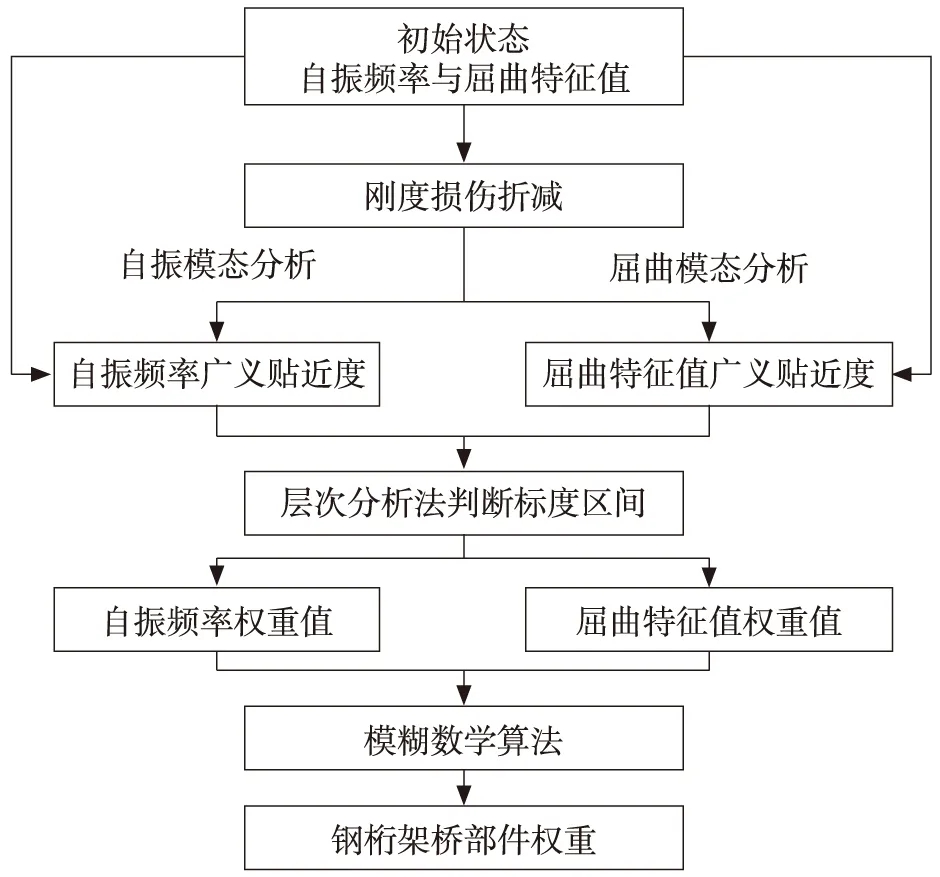
图4 部件权重分析流程

3.2 初始状态

初始状态桥梁前10阶自振频率及前10阶屈曲特征值如表1所示。由表1可见，第2与第3阶振型为桥门架弯曲、第5和第6阶振型为上平联弯曲。由此可见，不同部件对不同阶次的自振频率与屈曲特征值贡献不同。

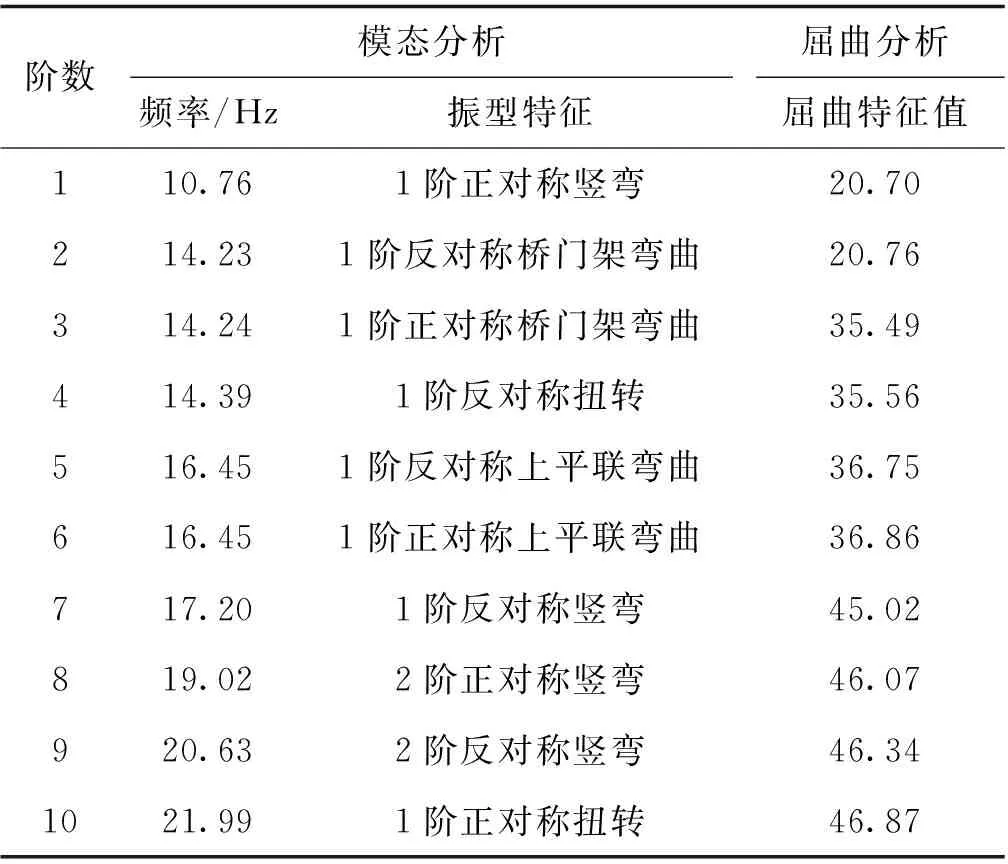
表1 初始状态自振频率与屈曲特征值

3.3 刚度损伤折减

结构损伤一般最终表现为截面刚度的降低，截面刚度取决于2方面：材料弹性模量和截面尺寸。本文采用弹性模量折减模拟部件损伤，每类部件设置3种损伤程度(刚度折减10%、20%、30%)，对应弹性模量折减为1.85×105MPa、1.65×105MPa与1.44×105MPa，覆盖桥梁运营过程中各个部件可能出现的不同损伤工况。

3.4 广义贴近度计算

通过计算得到每个损伤工况结构的前10阶自振频率与屈曲特征值。上弦杆与斜腹杆前10阶自振频率与屈曲特征值变化率如图5所示。由图5可见，上弦杆刚度损伤30%对第1阶自振频率折减达10.5%，远大于第3阶自振频率折减的0.4%，但对第1阶屈曲几乎没有影响；斜腹杆刚度损伤30%对第2阶自振频率影响最大达9.5%。这说明钢桁梁桥部件刚度损伤仅对特定阶次的自振频率及屈曲特征值有明显影响，对于部件权重分析需要综合考虑各部件对各阶自振频率及屈曲特征值的贡献。

广义贴近度是指2组数据序列之间的相似程度，表征桥梁损伤前后状态接近程度，其值越大表示状态越接近，反之则相离越远。考虑到各阶自振频率及屈曲特征值数值相对于初始数据存在均匀变化及非均匀变化，采用欧几里得贴近度[14]作为均匀性变化系数，斜率关联度[15]作为非均匀变化系数。分别计算各部件自振频率与屈曲特征值的广义贴近度，ai和bi分别表示损伤前后第i阶自振频率或屈曲特征值，损伤的广义贴近度为：

(a) 上弦杆自振频率

(b) 斜腹杆自振频率

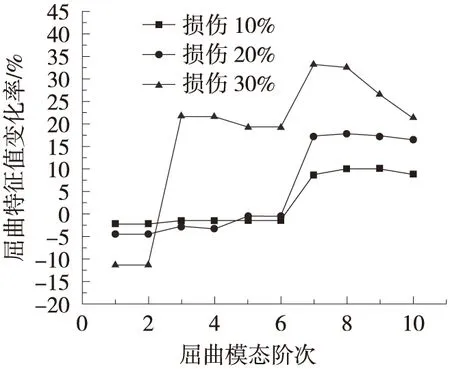
(c) 上弦杆屈曲特征值

(d) 斜腹杆屈曲特征值

δ′(ai,bi)=γ(ai,bi)×δ(ai,bi)

(1)

(2)

(3)

(4)

式中：δ′(ai,bi)为广义贴近度；δ(ai,bi)为均匀变化系数；γ(ai,bi)为非均匀变化系数；n为数据序列ai和bi的项数；ai为损伤前各阶自振频率或屈曲特征值；bi为损伤后各阶自振频率或屈曲特征值。

根据式(1)计算得到不同损伤前后各阶自振频率和屈曲特征值广义贴近度，结果如表2所示。从表2广义贴近度可以看出，对结构自振频率影响最大的3个部件为桥门架、桥面纵梁和上平联；对屈曲特征值影响最大的3个部件为上弦杆、桥面横梁和竖杆。

3.5 层次分析法判断矩阵标度区间

目前，层次分析法判断矩阵标度区间主要采用九标度法。为了划分部件权重层次分析法判断矩阵的标度区间，对比同一损伤工况不同结构部件的广义贴近度差值，得到自振频率最大差值0.297，最小差值0；屈曲特征值最大差值9.137，最小差值0.009。以最大差值与最下差值为上下限，将判断矩阵标度区间均匀分为9份，如表3所示。

表2 各个部件不同损伤工况广义贴近度

表3 判断矩阵的标度区间

3.6 部件权重计算

将钢桁架桥上部结构的组成部件用因素集B表示，因此待评价部件的因素集如下：B={B1,B2,B3,B4,B5,B6,B7,B8,B9}={上弦杆、下弦杆、竖杆、斜腹杆、桥门架、上平联、下平联、桥面横梁、桥面纵梁}。

综合考虑不同损伤程度的广义贴近度，采用式(5)计算损伤10%、20%、30%广义贴近度的平均值：

(5)

式中：δ′(Bi)为第i个部件的广义贴近度；δ′(Bi-j)为第i个部件损伤j的广义贴近度。各部件广义贴近度计算结果如表4所示。

表4 各部件广义贴近度

通过表4计算得到部件广义贴近度差值，并根据表3判断矩阵标度区间，分别建立自振频率判断矩阵C1与屈曲特征值判断矩阵C2。

将矩阵按行相乘并开方，然后进行归一化处理，得到部件权重向量：

ω1=(0.09 0.04 0.09 0.11 0.27 0.11 0.04 0.04 0.22)T

ω2=(0.30 0.10 0.17 0.07 0.04 0.06 0.04 0.190.04)T

为衡量采用最大特征值对应的特征向量作为部件权重与判断矩阵自身的一致性，定义一致性指标：

(6)

式中：λ为判断矩阵n阶互反阵的最大特征根；n为判断矩阵的阶数。

将一致性指标CI与随机一致性指标RI进行比较：

说明当前的部件权重计算结果具有较好的一致性。

3.7 原始权重修正

按上述方法计算得到的钢桁架梁桥各部件权重称为原始权重，分别反映部件损伤对桥梁自振频率及屈曲特征值的影响。为得到部件对桥梁整体结构的贡献，本文利用文献[7]中模糊综合评估模型选大算子，如式(7)所示，建立2种权重之间的合成关系，归一化得到最终评价集的权重，结果如表5所示。

(7)

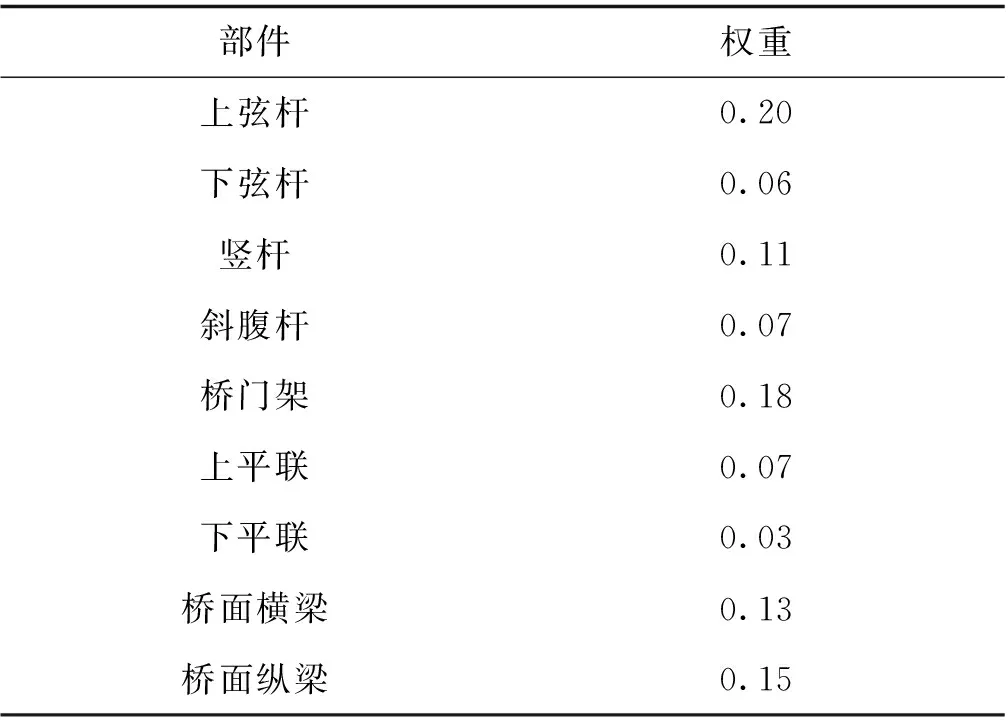
表5 钢桁架桥部件权重

4 结束语

1) 采用刚度折减模拟部件损伤工况，通过数值仿真研究了结构各阶自振频率与屈曲特征值的变化，提出了一套基于广义贴近度原理的钢桁架技术状况评定部件权重分析方法。

2) 基于本文提出的部件权重分析方法，得到钢桁架部件权重为：上弦杆0.20，下弦杆0.06，竖杆0.11，斜腹杆0.07，桥门架0.18，上平联0.07，下平联0.03，桥面横梁0.13，桥面纵梁0.15，可用于桥梁养护过程中的技术状况评定。