寒区水塘冰盖生长和消融分析

丁法龙，茅泽育

（清华大学水利水电工程系，北京 100084）

1 研究背景

静冰生消过程是寒冷地区冬季普遍存在的一种自然现象，多发生于湖泊、水库、水塘和流速较低的河流。冰盖的形成，一方面削弱了水体与大气之间的能量和物质交换，从而影响水体生态环境［1］；另一方面所产生静冰压力威胁水工建筑物的安全，如护坡工程的冰推破坏等。冰盖厚度是冰工程研究中重要的特征参数之一［2-4］，也是建立冰情灾害预报模式的关键物理参数之一［5-6］。另外，冰盖强度与厚度有关，因此冰盖厚度也是估算冰对水工结构物作用力、开展冰上交通以及冰期捕鱼等活动的重要参考指标。

冰盖厚度计算的数学模型分析方法主要是依据冰层生消物理过程建立热力及动力学数学模型，通过公式简化推导或者数值求解以确定冰厚。德国科学家Stefan基于冰层内部一维稳态热传导方程推导提出的冰冻度日法是最早的冰厚生长解析模型，此后又有学者根据冰冻度日法原理，通过实测数据拟合确定经验参数，研制出多种适用于当地气象和水文条件的衍生模型［7-8］。冰冻度日法及其衍生形式，将冰厚的发展过程与累积负气温联系到一起，具有应用方便、计算简单的优点，但同时也存在以下不足：（1）假定上表面冰温等于气温，即一维单相Stefan 问题，这已被实测证明是不合理的；（2）仅考虑了冰内热传导单一热力过程对冰盖厚度变化的影响；（3）当用于冰盖消融计算时，会不可避免地引入更多的经验参数或不确定项。

根据冰冻度日法，冰厚只有在气温转正后才开始减小，但实测资料显示，当气温尚低于0 ℃时冰盖厚度就已经开始减小，因此冰冻度日法是否适用于冰盖消融计算尚值得商榷。对于这个问题，众多学者进行了研究，提出了不同的解决方法，其中比较有代表性的有：Biello［9］以累积正气温修正冰厚最大值的计算方法模拟冰盖的消融过程，被称为融冰度日法；文献［10］通过修正Stefan公式中的经验参数，采用统一的公式对整个冰盖的生长和消融过程进行模拟；张学成等［11］在Stefan公式中增设了一个随机项并利用现场实测资料进行校核。这些方法或包含随机项，或包含经验参数，其预测精度显然受制于实测资料，不利于广泛应用，它们没有完善考虑影响冰盖消融的各个热力因素，仅侧重于冰厚对气温的依赖性，实际上，气温是通过影响大气与冰面之间的对流传热过程来影响冰盖生消的。

随着计算机技术和数值方法的进展，基于冰内热传导方程建立冰厚热力学数值模型，是一种便捷高效的研究手段，多位学者开展了这方面的研究工作［12-13］，但这些数值模型在边界条件设定时，往往对大气-冰面传热、辐射等热力要素存在不同程度的近似或简化，从而导致其计算结果与实际情况存在一定的差异。

静冰的生长和消融是一个主要发生在垂直方向上多层热交换、热传导的复杂过程，其热力因素包括冰盖上表面的太阳辐射、长波辐射、感热和潜热，冰盖下表面的水体传热，以及冰盖内的热传导，它们共同组成冰盖生消的热力条件。因此，冰盖热力学模型研究的是一个由大气-冰-水组成的热能耦连系统，精确的冰盖厚度计算应该立足于分析影响冰盖生消的各个热力过程，忽略其中某些热力要素甚至仅考虑冰厚对气温响应关系的计算模型是不尽合理的。

此外，截至目前，围绕静冰生消的研究多侧重于湖泊和水库，鲜有关于水塘的研究报道，相比于湖泊和水库，水塘的面积和水深更小，岸边和塘底对水体的热交换作用更为显著，在冬季冰盖形成之后，水体与冰之间的传热作用也更为显著，从而导致塘冰的生消表现出其特有的规律性。

为明晰寒区静冰生消过程，探究塘冰生消特性，本文通过分析影响静冰生消的各热力过程，建立生长期和消融期冰盖厚度计算的热力学模型，对黑龙江省大庆市青花湖8 号水塘进行冰情原型观测，采用塘冰观测数据对冰厚计算模型进行参数选定和模型验证，并基于塘冰温度链观测数据，分析表面冰温随气温和风速的响应关系、冰温垂向分布廓线、冰温和水温随时间的变化等规律，以期为寒区静冰生消分析及冰厚精确计算提供参考。

2 冰盖厚度计算模型

2.1 冰盖生长过程冰盖的生长可简化为一维热传导问题，描述为：

式中：Ti为冰的温度，℃；ρi为冰的密度，kg/m3；Ci为冰的比热容，J/（kg·℃）；t为时间；z为沿冰盖厚度方向坐标；λi为冰的热传导系数，W/（m·℃）。

式中：Qi为冰盖内部热传导的热通量，W/m2。

边界条件为：冰盖下表面冰温恒为冰的冰点Tm（即0℃）；冰盖上表面冰温为Ts。因此，由冰内热传导所决定的冰盖生长过程可表示为：

式中：hi为冰厚；L为冰的相变潜热，kJ/kg。

对式（3）进行时间积分，可以得到：

式（4）中假定冰盖上表面冰温Ts等于气温Ta，则得到著名的Stefan冰厚公式：

式中：AFDD为冰冻度日，等于日均负气温乘以天数的累积总和，即1AFDD=-1 ℃·d。

Stefan冰厚公式仅考虑了冰内热传导过程的影响，将大气-冰面对流传热和冰内热传导过程统一考虑，根据传热学理论称之为冰的传热过程，冰的传热过程两个环节的热通量表达式如下：

式中，Q为冰的传热过程的热通量，W/m2。

将式（6）改写成温差的形式：

将式（7）两式相加，消去温度Ts，整理后得：

综上，将冰的传热过程、水体-冰传热和辐射等热力因素综合考虑在内，则冰的生长过程可表达为：

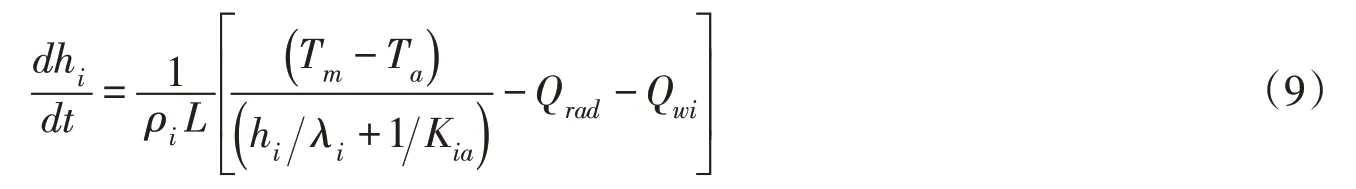
式中：Qwi为水体向冰盖下表面传热的热通量，W/m2；Qrad为冰面净辐射通量密度，W/m2；Kia为大气与冰面之间的对流传热系数，W/（m2·℃）。

将式（9）表达为时间增量的形式：

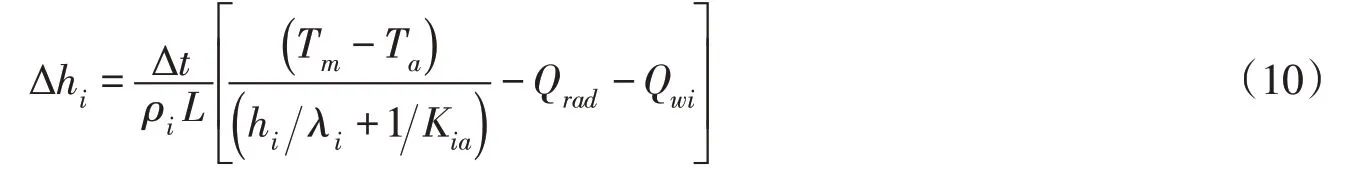
式（10）即静冰冰盖厚度生长的热力学模型。

2.2 冰盖消融过程研究表明［14］，在冰盖消融期间，气温在回升到0 ℃以前，辐射项占主导地位；当气温上升到0 ℃以上后，冰面对流热通量变得非常重要。基于该认识和上文冰盖生长期热力过程的分析，建立冰盖消融热力学模型如下：

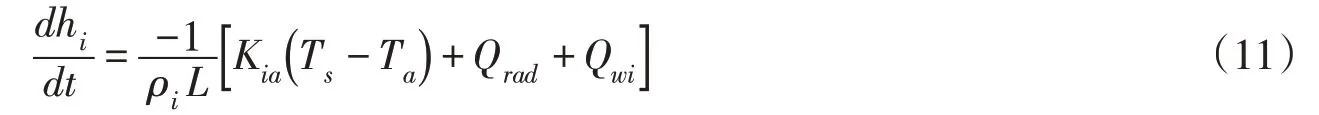
将式（11）改写为时间增量的形式：

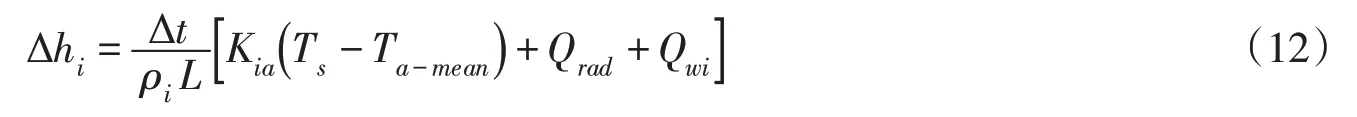
式中：Ta-mean为日平均气温，℃。

式（12）即静冰冰盖消融的热力学模型。

2.3 模型参数取值上述分析提出了生长期和消融期静冰冰盖厚度变化的计算模型（式（10）和式（12）），包含了对各热力过程的能量计算，模型中具体参数的取值如下。

2.3.1 大气-冰面对流传热系数Kia根据Ashton研究［15］，大气与冰面之间的对流传热系数Kia与风力等级大小有关，在无风（0级）与大风（8级）之间的常见风力范围内，Kia约为10～20 W/（m2·℃），其中无风时为10 W/（m2·℃），风级与Kia之间的关系列于表1，模型计算时的Kia取值结合现场观测期间的风力数据，由表1查取。

表1 Kia值与风力级别的关系

2.3.2 冰面净辐射通量密度Qrad（1）短波辐射（太阳辐射）QS。晴空无云遮时到达地面的太阳辐射通量密度QS-clear与纬度和日期有关，由气象研究结果［16］获得原型观测所在地区的晴空太阳辐射通量密度的季节变化过程，通过拟合回归得到下式：

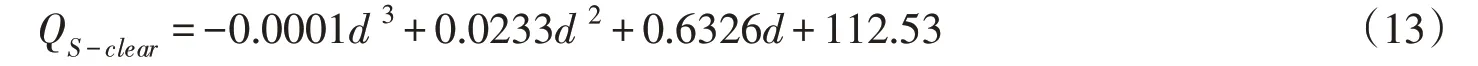
式中：QS-clear为晴空太阳辐射通量密度，W/m2；d为该日期在一年内的日序数，即1月1日的d为1，上一年的12月31的d为-1，本公式使用范围为-91 ≤d≤152，即上年10月1日至本年6月1日。

天空有云层时，太阳辐射由于云层覆盖而减少，云遮条件下的太阳辐射通量密度QS-cloud计算采用下式［16］：

式中：QS-cloud为云遮条件下的太阳辐射通量密度，W/m2；C为云量。

云遮条件下入射的太阳辐射又会在地表部分发生反射，因此，冰盖实际接收到的辐射通量密度为：

式中：QS为冰面实际接收到的净短波辐射通量密度，W/m2；A为反照率，对于冰面取值0.5［17］。

（2）长波辐射（地面辐射）QL。净长波辐射通量密度QL等于来自天空的入射长波辐射通量密度QL-in与冰面发出的长波辐射通量密度QL-out之间的差值，计算公式如下：

式中：QL为净长波辐射通量密度，W/m2；QL-in为来自天空的入射长波辐射通量密度，W/m2；QL-out为冰面发出的长波辐射通量密度，W/m2；k为经验系数，取0.18［17］；σ为Stefan-Boltzmann 常数，5.67×10-8W/（m2·℃4）；εi、εa分别为冰和大气的黑度。

2.3.3 水体-冰传热的热通量Qwi水体向冰的传热发生在冰盖下方极薄的水层内，其热通量的计算表达式：

式中：λw为水的导热系数，W/（m·℃）；dT/dz为极薄水层内的温度梯度，该温度梯度需要很高空间分辨率的精密测温仪器才能测得，存在较大困难。

针对湖水-湖冰传热过程的研究［18-19］表明，湖冰生长期及消融期前期的Qwi集中分布在5～7 W/m2值域内，考虑到水塘相较于湖泊，其水温更容易受到塘底的传热影响，结合前人研究成果，本文分别选取5种不同的Qwi值（6、8、10、12和14 W/m2）进行计算，结合冰厚观测数据，确定塘冰Qwi的合理取值。

2.3.4 其他参数 冰盖生消热力学模型式（10）和式（12）中的其他参数取值为：冰密度ρi取916 kg/m3，冰相变潜热L取335 kJ/kg，冰热传导系数λi取2.14 W/（m·℃）［18］，冰厚hi采用人工钻孔测量；冰盖上表面冰温Ts由温度传感器测得；气温Ta通过自行观测获得；日平均气温Ta-mean采用4 个定时平均法求得。

3 塘冰原型观测

3.1 观测场地概况静冰原型观测地点位于黑龙江省大庆市青花湖西侧，地处东经124°45′，北纬45°56′，湖区总面积28 km2。青花湖每年10月下旬至11月初开始结冰，冰盖到翌年4月中下旬融化，最大结冰厚度1.2～1.3 m。每年7—8月份给湖内补水，冬季结冰期停止补水，基本没有水位变动，因此青花湖的冬季环境接近静水水域，提供了静冰冰情观测的理想条件。青花湖西端的部分水域被人为地以浆砌石挡墙划分为若干水塘，本次观测选取塘底高程起伏较小的青花湖8号水塘为研究目标。青花湖8 号水塘呈东西长度120 m、南北宽度82 m的长方形布置，塘内水深2.4～2.6 m。

3.2 观测装置与方法根据对当地以往多年气温和冰情资料的分析，选择观测时段为2017年10月1日—2018年5月1日，和2018年10月20日—2019年4月29日。观测地点的气象数据由A753 WS 无线自动气象站提供，包括气温、空气湿度、风速和风向、气压等；冰温及水温测量采用罗汉姆公司生产的RH-8068热电阻PT100铂热电阻温度传感器测定，测温精度±0.05 ℃；温度数据采集至CR1000X 数据采集仪，数据采集频率为10 min/次。

温度测点位于水塘中心处，从冰面至冰下布设一条温度观测链，观测链上安装有18个PT100温度传感器探头，以记录冰温和冰下水温，冰下温度探头随冰生长会冻结到冰内以记录冰温。温度探头的垂向布设位置为：冰盖上表面处（观测冰盖表面冰温Ts）；冰面以下10、20、30、40、50、60、70、80、90、100、120、140、160、180、200、220和240 cm。观测链采用木质框架固定，选择木质材料的原因是木头的导热系数低，对冰层的热影响较小。观测链导线连接在支架上，支架固定于预先埋设的混凝土管桩之间，温度观测链布置如图1所示。冰厚采用冰钻穿孔后用塔尺于每日12时进行测量，在温度测点附近选择3个冰厚测点，采用3个测点的平均值作为每个采集日期的冰盖厚度。

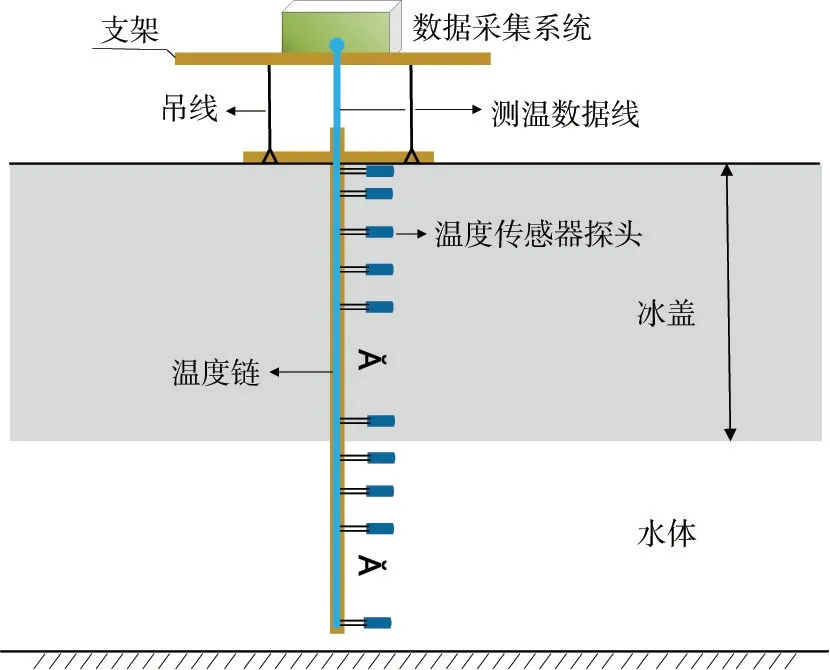
图1 冰情原型观测

4 结果与分析

4.1 气象条件及冰厚历程分析青花湖以往多年气象数据，青花湖每年10月份至次年4月份的日平均气温的多年平均值在-18.9～-12.3 ℃之间，冬季累积负气温在1458～2053 ℃之间，风力级别多年平均集中在0～5级范围内。图2展示了2017—2018年观测期间的日平均气温、风速和云量数据。观测期间的日平均气温的平均值为-14.97 ℃，低于同期多年平均值-2.26%。平均风速3.1 m/s，属3级风力（微风）；云量主要集中在0（晴空）～3级之间。

青花湖冰封期持续约5～6 个月，地面平均冻深1.63 m，最大冻深1.86 m，最大结冰厚度1.2～1.3 m之间。在观测的2017—2018和2018—2019两个年份：结冰起始日期分别为10月27日和10月22日；最大冰厚日期分别为3月16日（冰厚114 cm）和3月9日（冰厚106 cm）；冰盖消失日期分别为4月21日和4月15日。2017—2018年冰期时长为176 d，其中生长期139 d，平均生长速率0.82 cm/d；消融期37 d，平均消融速率3.08 cm/d。2018—2019年冰期时长为174 d，其中生长期137 d，平均生长速率0.77 cm/d；消融期37 d，平均消融速率2.86 cm/d。

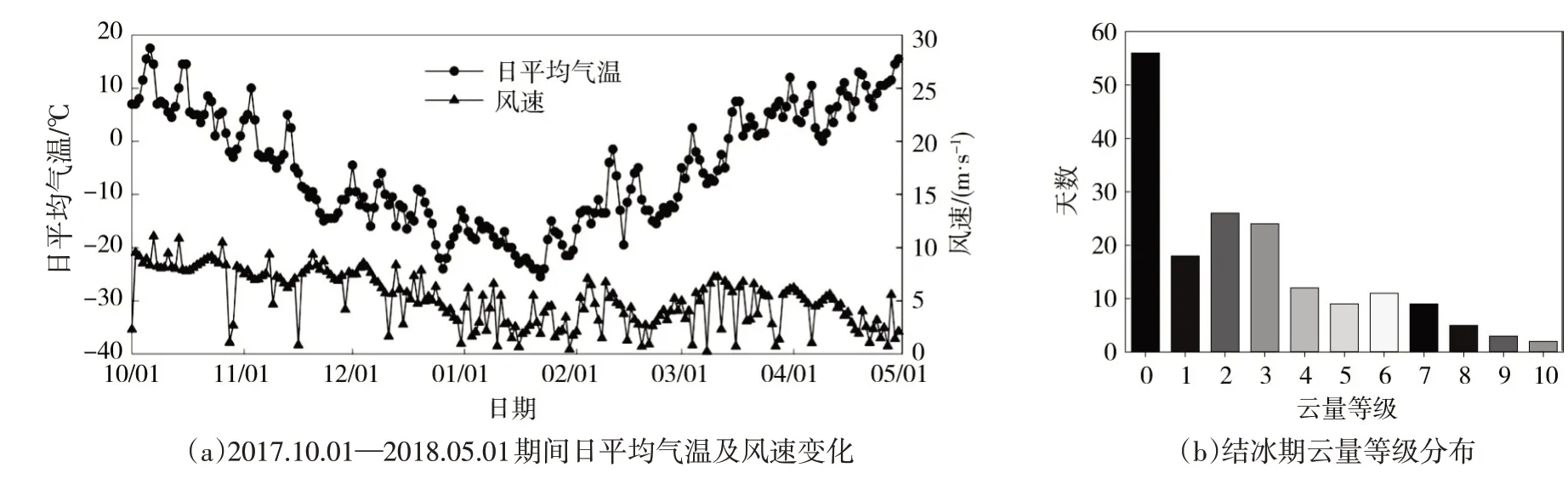
图2 2017—2018年冬季气象资料

4.2 冰厚计算模型验证根据冰厚计算热力学模型式（10）和式（12），代入日平均气温、风速、云量等气象数据和表面冰温等观测数据，分别选取不同的水体-冰传热的热通量，逐日计算2017—2018年冰盖生长期和消融期的厚度变化，结果如图3和图4所示。需要说明的是：（1）水体-冰传热的热通量Qwi是时间变量，本文不研究其具体的时间变化过程，本文及文献［18-19］中Qwi的取值均为时间平均值，不同的是文献［18-19］中将冰盖生消全过程的Qwi进行平均，本文则对生长期和消融期分别取平均值；（2）严格地说，冰的热传导系数λi也是时间变量，在封冻、稳封及消融的不同阶段，由于冰层组成类型、冻结密实度、冰层内部温度分布的变化，冰的热传导系数λi也随之发生相应变化。由于冰热传导系数的时空变化规律十分复杂，因此至今国内外在进行冰厚生消计算时，多采用常数值代替，不同学者对这个取值亦有所差异，本文采用了Matti Lepparanta［17］在湖冰研究时的取值，即2.14 W/（m·℃）。

图3中，水体-冰传热热通量Qwi分别取值6、8、10、12和14 W/m2时，冰厚计算值与观测值之间的均方根误差RMSE分别为3.6、1.9、1.3、4.8 和5.9 cm，即当Qwi取10 W/m2时，生长期的冰厚计算值与观测值最为接近，这比前人湖冰研究成果中的取值稍大，这是因为相比于湖泊，水塘的面积和水深更小，导致岸边和塘底对水体的热交换作用和水体向冰的传热作用更为显著，从而使得其Qwi值更大。

图3 2017—2018年冰盖生长期的冰厚变化过程

图4中Qwi分别取值6、8、10、12和14 W/m2时，冰厚计算值与观测值之间的均方根误差RMSE分别为6.7、4.6、3.8、2.3 和5.2 cm，即冰盖消融期Qwi的最佳取值是12 W/m2，比生长期的10 W/m2更大，这是因为在冰盖消融期间，气温回升及太阳辐射通量密度增强，均使得塘内水体温度升高，导致水体与冰盖交界面处的温度梯度增大，因此水体向冰盖的传热作用更强。上述结果表明，水体向冰的传热可显著影响冰盖的热力生消过程，忽略该热力因素或者选用不合适的热通量Qwi值，都会造成冰厚计算的误差。

根据2017—2018年冰期的冰厚计算结果，分别选定10和12 W/m2作为生长期和消融期冰厚计算模型中Qwi的最佳值，并对2018—2019年的冰厚进行计算和实测对比，结果如图5所示。斯皮尔曼等级相关系数用于表征两个定序变量之间的相关性，本文引入该相关系数（以P表示），来定量评估实测冰厚历程曲线与计算冰厚历程曲线之间的相关度。由图5可见，冰厚计算值与观测值吻合良好，冰盖生长期和消融期的斯皮尔曼等级相关系数分别为0.96和0.92，表明本文提出的冰厚计算模型具有一定的合理性，结合场地气象条件和水文条件选择合理的模型参数，可以较为精确地预测静水冰冰盖厚度的生消演变过程。

图4 2017—2018年冰盖消融期的冰厚变化过程

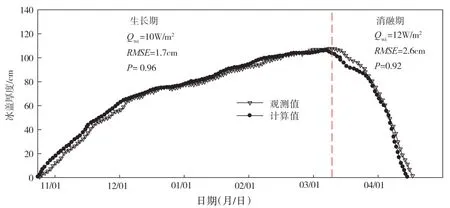
图5 2018—2019年冰厚生消过程计算值与观测值对比

4.3 温度链观测数据分析温度链对观测期内的表面冰温、冰层内冰温和冰下水温进行了持续监测。表面冰温由大气和冰面之间的热交换所决定，并与冰内的热传导过程相耦合，难以通过热力过程分析确定，以往研究多是通过建立其与气温之间的经验关系来估算表面冰温的大小。由上文的分析可知，大气与冰面之间的对流传热与风力大小有关，即相同负气温条件下，不同的风力等级可能会形成不同的表面冰温。根据塘冰观测数据，对表面冰温Ts作两因素方差分析，两个预设影响因素分别为气温Ta和风速Vw。方差分析结果表明，当取显著性水平为5%时，表面冰温Ts与气温Ta和风速Vw均显著相关。对表面冰温Ts作多元回归分析，得到Ts随Ta和Vw的变化关系表达式：

式中：Vw为风速，m/s。

式（20）回归模型的统计量中，相关系数R2为0.937，残差的方差为0.084，回归结果的残差离零点均较近，且残差的置信区间均包含零点，说明回归模型能较好的符合原始数据。图6为选取的典型气象条件下的表面冰温观测值与式（20）计算值的对照，从图6中可以看出，表面冰温计算值与实测值集中均匀分布于1∶1正比例直线附近，计算值的平均相对误差为4.72%，预测效果较为理想。

冰层内部的冰温是冰的基本状态参量，图7为2018年3月1日至3月2日不同深度冰层的冰温及气温变化。由图7可见，冰温变化与气温的波动存在一定的响应关系，但各层冰温随随时间的波动较气温更为平缓，表层（10 cm）冰温变化与气温变化趋势较为一致，随着冰层深度的增加，冰温波动幅度逐渐减小，冰温也逐步升高。气温对冰温的影响深度至多可达30 cm，冰层深度30 cm以下的冰温随时间变化近似一组水平直线。冰温与气温最小值出现于每日6时—7时，冰温比气温大约滞后1 h，最大值出现在下午12时—16时，冰温滞后约2 h。

图6 表面冰温计算值与观测值对比

图8为2018年12月15日不同时刻的冰温垂向分布，由于冰层上部受气温变化影响显著，因此冰温垂向分布廓线的上半部分（30 cm以上）冰温随时间变动较大；下半部分（30 cm以下）冰温基本呈线性分布，这与图7反映的规律基本相同；同一冰深位置的冰温日平均值沿冰深呈良好的线性分布。

图7 不同深度的冰层温度变化（2018.03.01—2018.03.02）

图8 2018年12月15日不同时刻的冰温垂向分布

冰下水温是控制冰下热通量的关键，它直接同冰底面融化速率有关［20］，这一点也可由本文关于水体-冰传热的热通量对冰厚计算影响的分析可见。图9为2017—2018年冰期内冰盖下不同水深处水温的时间变化过程。由于冰盖厚度处于不断的生消之中，这里的水深指当日自冰盖底部以下的垂向位置；水温取当日2、8、14和20时这4个不同时刻的平均值。

由图9可见，在冰盖生长期，受负气温的持续影响，冰下水体持续降温，越靠近冰盖水温越低，整个水体在垂向上呈逆温分布，最高水温出现在塘底，约为3.5～4.3℃。随着水深的增加，水温变化速率逐渐减小。在冰盖消融期，3月19日之前水温变化较为缓慢，3月20日之后，冰盖逐层消融，水体温度整体快速回升，最大升温速率可达0.13 ℃/d。不同时期的水温沿垂线方向均呈良好的线性分布，但每日不同时刻的垂向分布趋势略有差异。

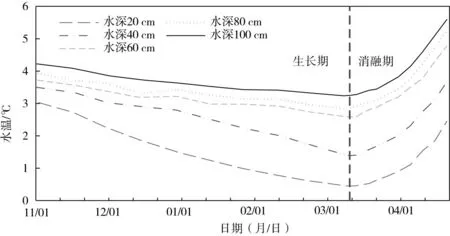
图9 2017—2018年冰期冰盖下不同水深处的水温变化

对比冰盖生长期和消融期的水温变化：生长期水温持续降低且变化速率较为缓慢，主要是受气温变化的影响；消融期水温先是缓慢回升，随后快速升高且变化速率高于同期的气温回升速率，因此，消融期水温的升高应是受到气温转正、地温升高以及太阳辐射增强等多个作用的综合影响。

5 结论

（1）通过分析静冰生消的各热力要素，考虑大气-冰面对流传热、冰面辐射（短波辐射、长波辐射）、水体-冰传热过程，建立了生长期和消融期静冰冰盖厚度计算热力学模型，并给出了模型中相关参数的取值。（2）针对黑龙江省青花湖8号水塘，分别选取不同的水体-冰传热热通量Qwi进行了冰厚计算，实测资料显示生长期和消融期的最佳Qwi值分别为10和12 W/m2，这比湖冰研究中的取值更大，是因为水塘的面积和水深更小，导致岸边和塘底对水体的热交换作用和水体向冰的传热作用更为显著，从而使得其Qwi值更大。（3）采用参数优化后的冰厚计算模型对2018—2019年的冰厚历程进行了计算，计算值与观测值吻合良好，生长期和消融期的斯皮尔曼等级相关系数分别为0.96 和0.92，表明本文提出的冰厚计算模型可以较为精确地预测静冰厚度的生消过程。（4）对观测到的表面冰温数据作方差分析，结果表明，表面冰温Ts与气温Ta和风速Vw均显著相关；通过多元回归分析得到了Ts随Ta和Vw变化的关系表达式。（5）冰层内的冰温变化与气温的波动存在一定的响应关系，且上层冰温变化与气温变化趋势较为一致，随着冰深增加，冰温波动幅度减小；黑龙江省青花湖8号水塘的观测资料表明，气温对冰温的影响深度至多可达30 cm，冰温与气温最小值出现于每日6 时—7时，冰温比气温大约滞后1 h，最大值出现在下午12时—16时，冰温滞后约2 h。（6）冰下水体温度在垂向上呈逆温分布；在冰盖生长期，冰下水体持续降温，随着水深的增加，水温变化速率逐渐减小；在冰盖消融期，水体温度先缓慢随后快速回升，最大升温速率可达0.13 ℃/d。

致谢：感谢通威股份有限公司王小平在冰型观测中给予的帮助。