高拱坝-地基体系整体稳定概率地震风险分析

梁 辉，赵文光，郭胜山，涂 劲，李德玉，廖建新

（1.中国水利水电科学研究院，北京 100048；2.中国电建集团成都勘设计研究院有限公司，四川成都 610072；3.中国三峡建设管理有限公司，北京 100038）

1 研究背景

基于概率的地震风险分析在地震工程中越来越受到重视，已经广泛应用于土木工程系统以及工程结构的抗震性能评估中。其能够从概率的角度对结构抗震性能进行评价，并且能够合理评估地震作用导致的结构不同性能水平，及其可能带来的经济损失，为工程结构的维修加固提供科学依据。

Benjamin［1］考虑了模型的不确定性，提出了基于概率的风险分析框架，针对堤坝开展了风险分析，通过决策树对溃坝引起的经济损失进行了评估。Karaa等［2］基于贝叶斯方法，提出了能够考虑工程不确定性、风险偏好和经济损失的抗震安全评估和风险分析方法，并针对土石坝开展了相关研究。Vick等［3］描述了概率风险分析在岩溶地区堤坝设计的应用，通过概率模型，对堤坝安全风险进行了评估。Yegian等［4］为了针对土石坝进行地震破坏或坍塌风险评估，提出了地震风险分析方法，包括地震危险性分析、结构抗震性能分析以及两者相结合的地震风险分析，在地震危险性分析中将未来地震的发生以概率的形式描述成地震动强度和地震动运动周期的函数，在结构地震性能分析中提出了一种计算土石坝永久变形的概率分析方法，分析中采用地震动加速度、周期和卓越周期来表征地震事件。Lave等［5］总结了大坝风险分析和管理存在的一些缺陷，认为目前高风险大坝的安全标准应侧重于降低财产损失（包括大坝损坏）和防止洪水造成的死亡损失，随后其提出了大坝风险分析和管理的一套新方法。Lupoi等［6-7］首先采用地震风险评估方法对钢筋混凝土结构开展了基于概率的抗震设计和评估，随后在考虑力学参数的不确定性下对该方法进行简单扩展，并应用于钢筋混凝土桥梁结构的地震风险评估中。Ellingwood等［8］对地震风险分析中不确定性建模进行了阐述，并对不确定性如何在钢筋混凝土建筑结构地震风险评估分析中传播进行了解释。Hariri-Ardebili［9］对大坝的风险分析和可靠性分析的研究进展进行综述，以期能够提高研究者们对概率风险分析的认识。随着我国水利水电工程的快速发展和建设，众多研究者和设计人员也开展了大坝风险分析相关研究，但大多局限于洪水灾害风险分析研究［10-13］。金峰等［14］针对开展了基于功能的高坝风险分析研究，提出了一种计算高坝在不同地震强度下的震害损失方法。张楚汉等［15］对高混凝土坝抗震安全评价的研究成果进行了分析和总结，针对高混凝土抗震研究发展方向给出了建议，提出了综合考虑社会、经济、环境与工程的混凝土坝抗震安全风险评价体系研究思路。沈怀志［16］分别针对不同破坏模式开展了重力坝的抗震安全评价和风险分析研究。姚霄雯［17］分别基于不同的位移指标开展了混凝土高拱坝的地震易损性分析和抗震安全评估，并基于风险分析结果对拱坝进行了抗震加固优化分析。陈建云等［18］基于概率统计框架提出了一种混凝土坝全寿命周期抗震性能概率分析方法，引入相对位移角作为评价指标，给出了混凝土坝时变动力可靠度。

综上所述，目前绝大多数研究成果集中于土坝或者堤坝的风险分析等，且主要是针对洪水灾害开展的大坝概率风险分析研究。而在现行的抗震设计规范中，地震荷载组合工况往往成为高坝抗震设计的控制性工况，因而需要进一步加强基于概率的混凝土坝抗震安全评估研究。

2 概率地震风险模型

概率地震风险分析作为新一代基于性能的抗震设计重要环节之一，已经被广泛应用于工程结构的抗震安全评估。开展结构概率地震风险分析的主要步骤包括：（1）定义工程场址地震动强度和其对应的重现期，此即地震危险性分析；（2）建立地震动强度与结构动力响应需求参数之间的关系，即结构概率地震需求模型的构建；（3）开展一系列不同概率水平地震作用下的结构动力响应分析，并对计算结果进行统计分析，绘制结构地震易损性曲线，即结构地震易损性分析；（4）综合以上步骤，构建结构地震响应需求参数年超越概率模型，绘制结构超过某一性能水平概率地震风险分析曲线。

2.1 地震危险性分析地震危险性分析曲线描述了不同地震动强度参数的年超越概率，其中地震动峰值加速度在数学上通常采用极值Ⅱ型的最大分布函数来描述：

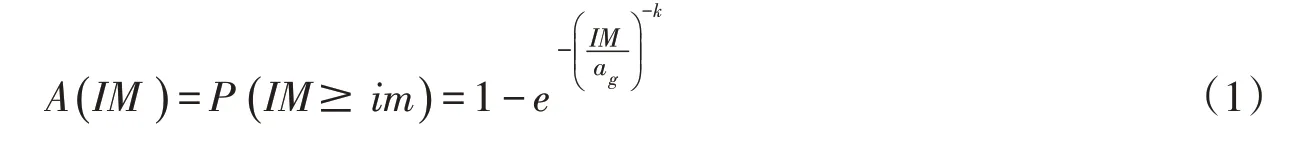
式中：IM（intensity measure）为地震动强度参数，本文中指峰值加速度；im为地震动强度值；ag为众值加速度，为位置参数；k为形状参数。

既有研究表明［19］，可以采用幂指数对式（1）进行近似，即：

式中：vIM(IM) 为地震动参数IM的年超越概率；K0、K分别为形状常数，可以通过设计地震（maxi⁃mum design earthquake，MDE）和校核地震MCE（maximum check earthquake，MCE）对应地震动强度拟合求得：

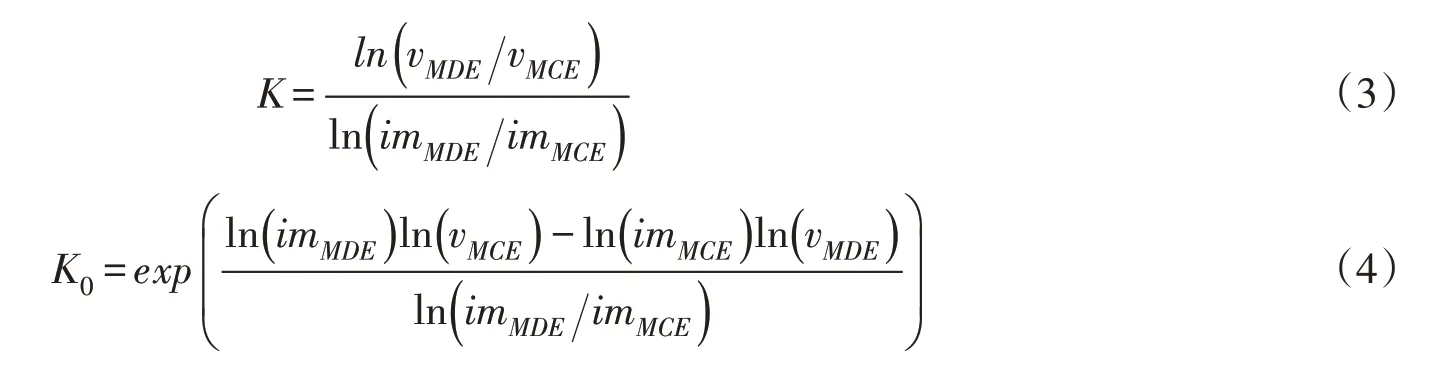
式中：MDE对应于100年超越概率为2%；MCE对应于100年超越概率1%；vMDE、vMCE分别为MDE和MCE的年超越概率；imMDE、imMCE分别为MDE和MCE对应的地震动强度，本文为地震动峰值加速度（peak ground acceleration，PGA）。

2.2 概率地震需求模型概率地震需求模型，顾名思义即为地震动强度参数与结构工程需求参数的关系，它描述了在给定地震动强度下，结构或者体系超过一定性能水平的概率。结构的概率需求D一般可以写成结构地震响应需求D的中位值mD|IM和随机误差ε的乘积：

式中，随机误差ε服从对数正态分布，中位值为1，对数标准差为βD|IM。

由此可得，在给定的地震动强度im下，结构地震响应需求D服从对数正态分布，其数学描述如下［20］：

式中：D为结构地震响应需求参数；d为某个给定的结构地震动响应值。

文献［20］研究得到，结构地震响应需求参数D中位值mD|IM与地震动强度参数IM之间的关系在数学上一般可以采用幂指数函数进行描述：

对式（7）两边同时取对数，可得：

由此，基于结构非线性动力响应分析结果，采用式（7）或者（8）进行指数或者对数线性拟合，即可得到系数a和b。对数标准差βD|IM计算公式如下：

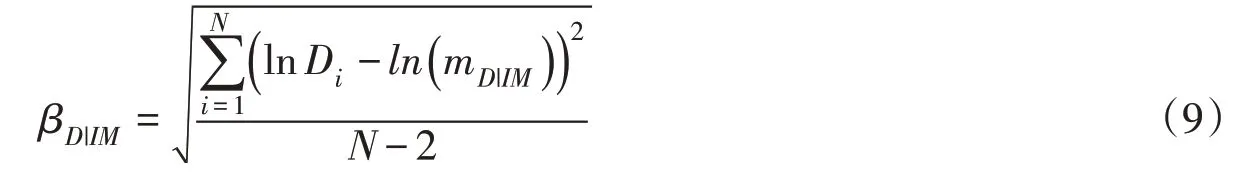
其中，N为回归分析的总数据点数。

概率地震需求模型中地震动强度与结构地震响应参数之间的相关性可以通过拟合系数b和对数标准差βD|IM来描述，其中对数标准差βD|IM主要表征概率地震需求模型的有效性，其值越小越好，拟合系数b描述了概率地震需求模型的敏感性，该值越大，表明地震动强度指标与结构动力响应参数的敏感性越大，相关性越好。

2.3 地震易损性分析模型结构地震易损性分析可以定性地描述为在不同概率水平的地震作用下，结构达到某一级别性能水平的概率，其是概率地震风险分析的一个重要环节。目前，鉴于混凝土坝的实际震害资料相对较少，解析地震易损性分析方法得到了广泛地应用。解析易损性分析方法主要分析内容有：结构动力响应分析、极限状态或性能水平的定义以及地震易损性曲线的形成。划分结构多级性能水平和定义相应的阈值是开展地震易损性分析的前提，依据所定义的性能水平，采用以下步骤可以得到结构地震易损性曲线。

（1）结构在某一特定地震动强度下达到某一极限状态或性能水平的概率可以采用下式求得：

式中：P()LS|IM=im为在地震动强度im下结构达到某一性能水平或极限状态LS的条件概率；N、M分别为所抽取随机样本数和地震动的数量；NLS为在N×M次大坝计算分析模型中在每个地震动强度下超过某一性能水平或极限状态LS的数量。

（2）易损性曲线是基于式（10）统计所得到的数据，通过采用不同的概率分布函数进行拟合得到。目前，在结构动力分析中应用比较广泛的易损性曲线解析函数为对数正态分布函数［21-23］，即：

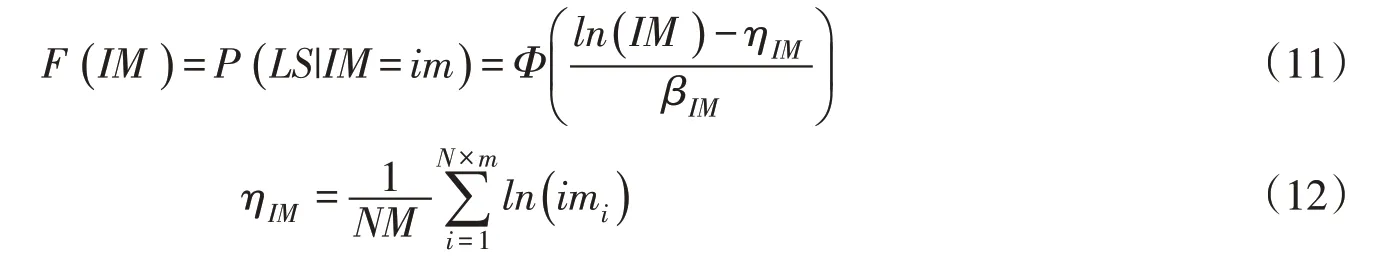
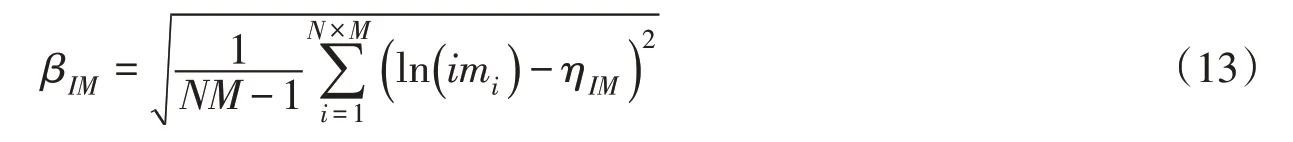
式中：F(IM) 为地震动强度im下，混凝土坝达到某一性能水平或极限状态LS的概率；Φ(·)为标准正态分布函数；ηIM、βIM分别为地震动强度参数IM的对数平均值和对数标准差。

2.4 概率地震风险分析模型概率地震风险分析通常可以描述为：地震危害性=地震易损性×地震危险性。概率地震风险分析函数，即结构动力响应超过某一性能水平的破坏年超越概率vD(d)可以由地震危险性分析函数（式（2））和结构地震易损性分析解析函数（式（11））的卷积给出：

或者如下式：

将式（2）带入式（16），且结合式（11）可得：

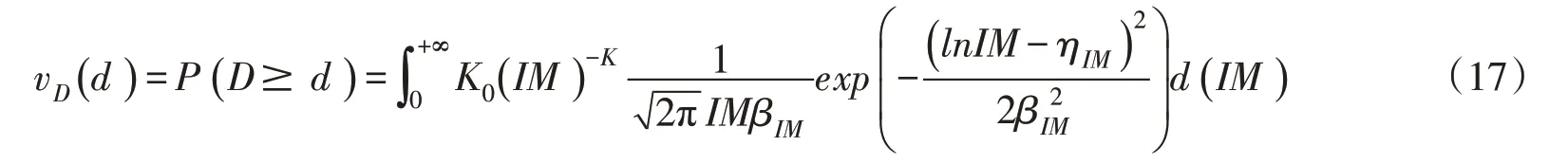
将式（17）进一步化简，可以得到：

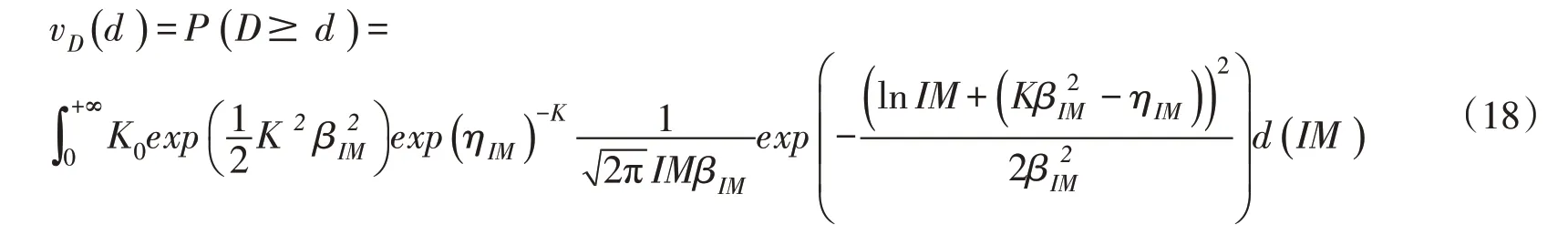
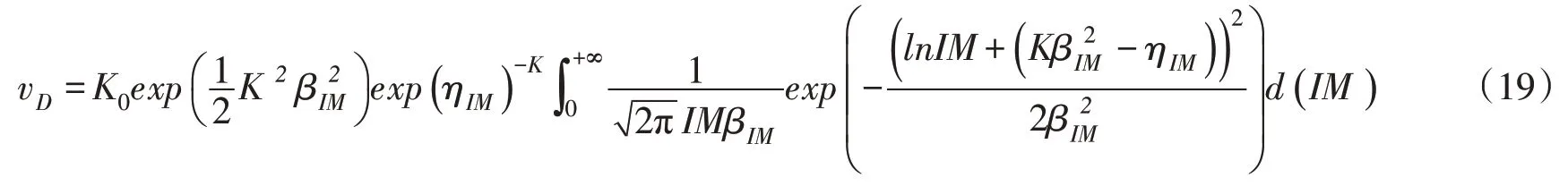
由积分项：

式中：d为结构动力响应；a、b和βD|IM分别为结构概率地震需求模型中的拟合系数和对数标准差；K0、K分别为地震危险性分析函数的形状常数。

由此，依据式（21）即可得到结构地震响应超越某一性能水平的年超越概率曲线，再依据年超越概率P1与设计基准期限T0时间内超越概率PT0之间的关系，即可求得在设计基准年限内结构达到不同性能水平的超越概率PTn(di)，最后依据下式可得到结构达到各个性能水平的概率：

综上所述，基于地震危险性分析和所建立的概率地震需求模型，结合地震易损性分析成果，采用式（21）和式（22），即可开展高拱坝-地基体系整体稳定概率地震风险分析。

3 拱坝坝肩抗滑稳定地震风险分析

3.1 模型建立

3.1.1 有限元模型 该双曲拱坝坝高289.0 m，其坝顶高程为834.0 m。坝顶厚度14.0 m，最大拱端厚度83.91 m。坝址区域河谷左岸相对较缓，右岸比较陡峻，河谷呈不对称的“V”字型。坝址位于设计烈度为Ⅸ的强震区域，同时坝肩存在大量的缓倾角结构面、断层和裂隙等。这些不利的、复杂的地质条件构成了强震作用下拱坝坝肩可能发生失稳的地质背景。根据该高拱坝坝区地形地质的特点，建立拱坝-地基系统的三维有限元网格来开展高拱坝坝体-地基系统整体抗震稳定分析研究。大坝-地基体系三维有限元网格模型见图1。地基基础区域分别沿顺河向、横河向和竖向延伸至坝高的2倍。整个有限元模型采用三维块体单元进行离散，坝体沿厚度方向布置6层三维块体单元，整个模型总结点数约为13×104，单元数约为123×104。

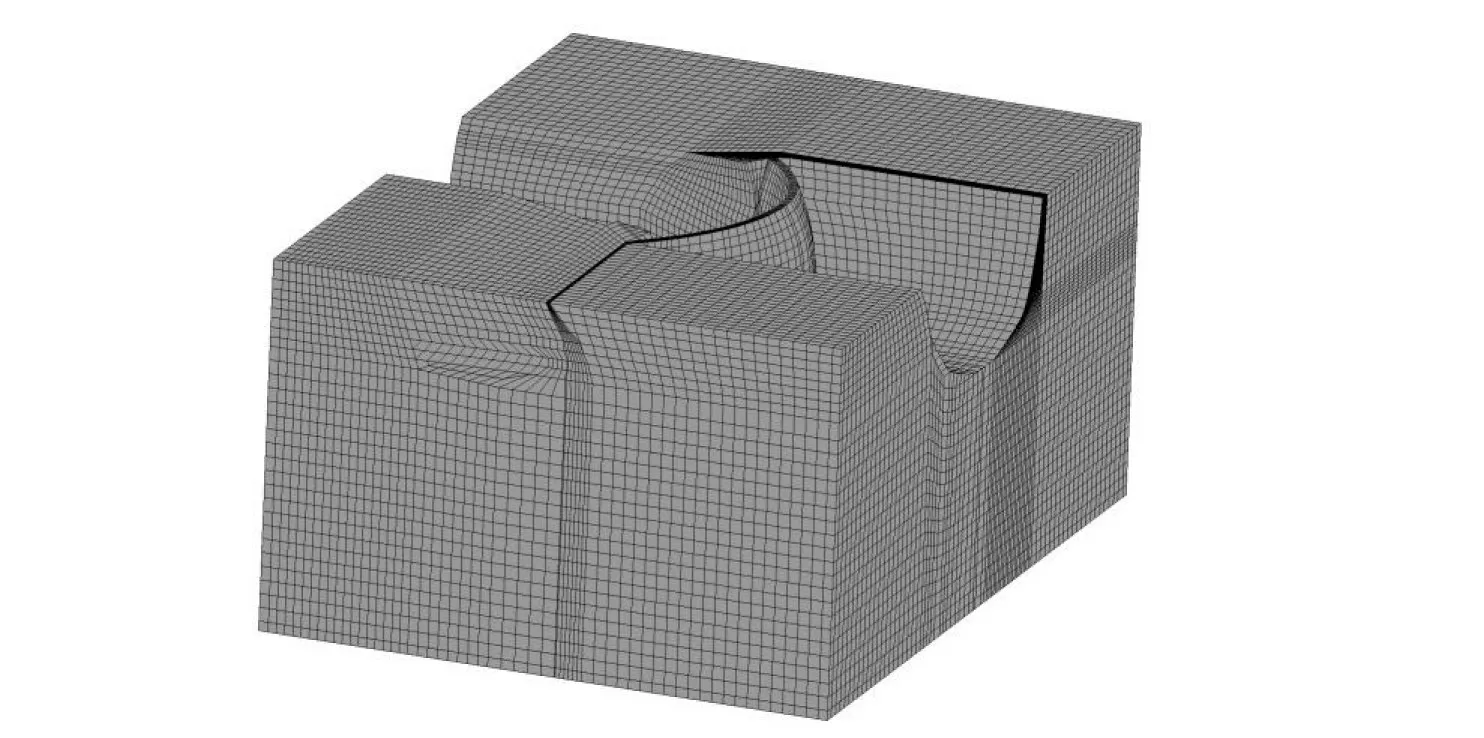
图1 大坝-地基体系三维有限元网格模型

图2 右岸可能滑块及其结构面组成

考虑到工程地质勘探所考查的工程地质实际情况和模型计算简化，本文选择右岸潜在的滑动块体来研究拱坝的地震稳定性，如图2所示。由图2（a）所示，滑动块体通过底滑面、侧滑面、拉裂面和上游开裂面以及下游临空面构成，有限元建模过程中将构成潜在的滑动块体的构造面均作为缝面进行处理，其各个构造面见图2（b）。鉴于拱坝横缝的张开和闭合是影响其抗震性能的重要因素［24-27］，本文依据实际设计要求对坝体28条横缝进行模拟，其横缝的布置以及相应的编号见图3。同时，对于拱坝，大坝-地基交界面是大坝抗震设计的薄弱位置［28］，为了反映坝基交界面的破坏情况，模型中在这一薄弱位置设置了具有抗拉强度和抗剪强度的双节点动接触边界，其交界面模型见图4。图5描述了本文所选取的右岸滑块底滑动面特征点位置，节点编号为6272。

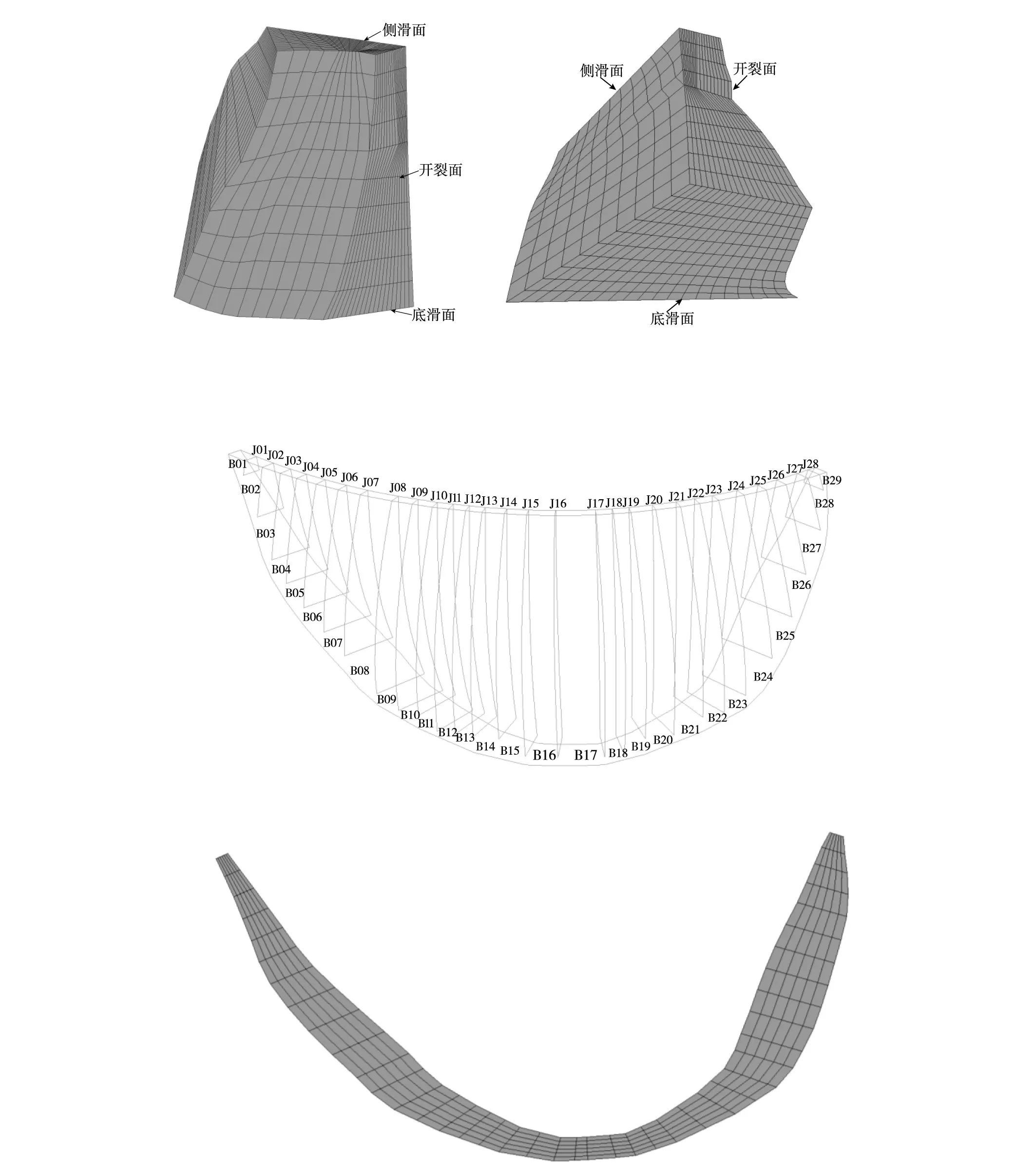
图3 大坝横缝布置及相应编号

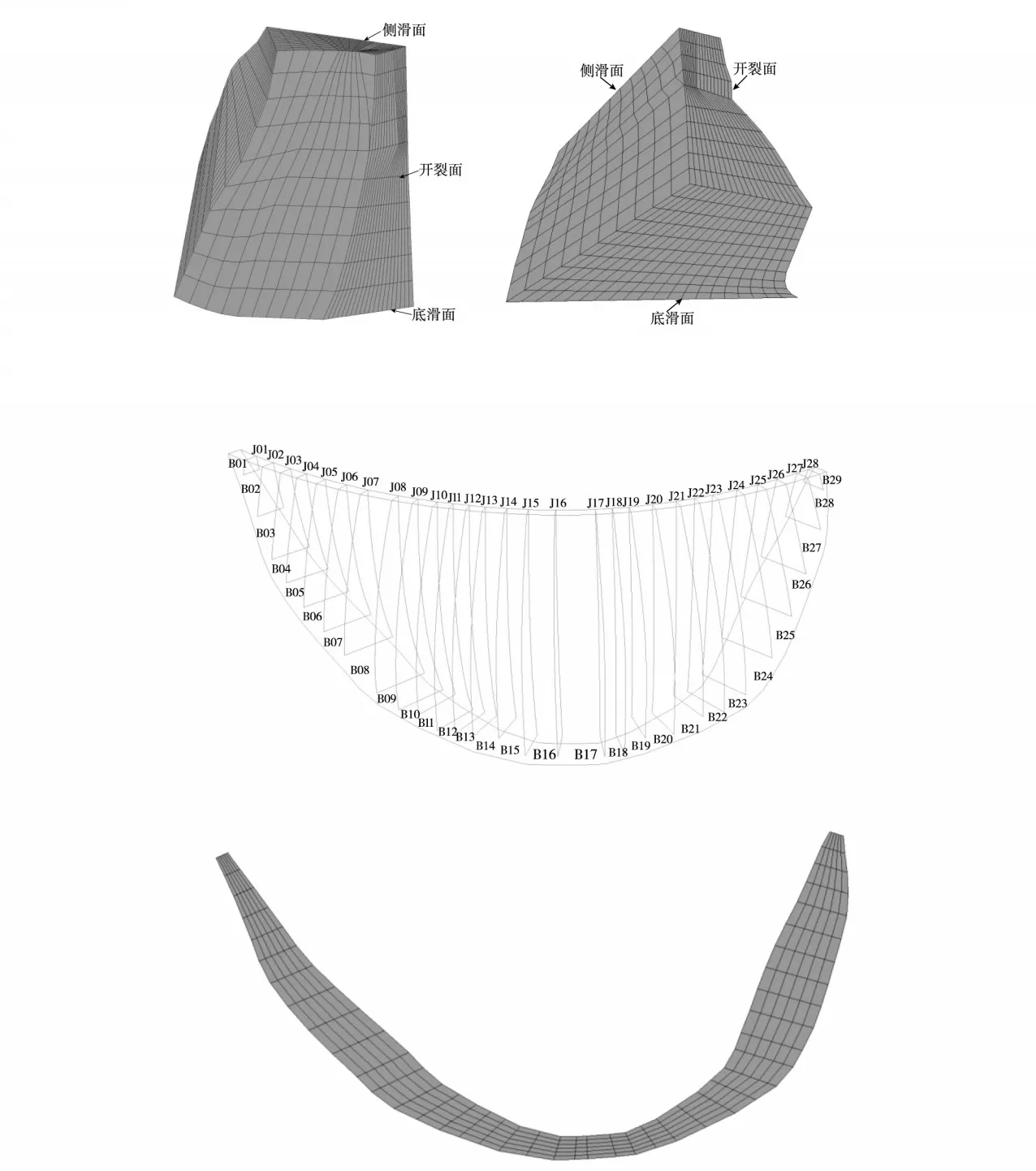
图4 坝体-地基交界面

图5 底滑面特征点

坝体混凝土材料参数分别为：静态弹性模量24.0 GPa，泊松比为0.167，密度为2400.0 kg/m3，动态弹性模量取为静态弹性模量的1.5倍，线膨胀系数6.5×10-6℃-1。基岩材料按实际分层考虑，各层平均静态综合变形模量约为11.0 GPa，泊松比约为0.23，密度为2700.0 kg/m3。坝基交界面的初始抗拉强度为3.42 MPa，抗剪强度参数摩擦系数和凝聚力分别取值为1.15和1.10 MPa。计算分析中，采用黏弹性人工边界模型计入地基辐射阻尼的影响，采用不计入库水可压缩性的Westergaard附加质量法来考虑坝体-库水相互作用。由于本文是针对拱坝坝肩地震稳定性的研究，潜在的滑动块体接触面上的抗剪强度参数的影响远远高于混凝土和基岩的弹性模量的影响，因此，将潜在的滑动块体的构造面上的摩擦系数和凝聚力作为随机变量来开展参数敏感性研究。其分别定义为：底滑面摩擦系数μbottom和凝聚力cbottom、侧滑面摩擦系数μside和凝聚力cside以及上游拉裂面摩擦系数μcrack和凝聚力ccrack。同样地，依据文献［29］，滑动块体的构造面上的摩擦系数与凝聚力的概率分布分别取为正态分布和对数正态分布。滑块各滑动面材料特性以及相应的概率分布见表1。

表1 滑动面上摩擦系数和凝聚力参数值以及其对应的概率分布

3.1.2 静动荷载 计算分析中，静态荷载包括坝体自重、正常水位下的上下游水荷载、上游坝前淤沙荷载和温度荷载。上、下游正常水位分别为825.0 m和604.0 m。上游坝前淤沙高程为710.0 m，淤沙的容重和内摩擦角分别为5.0 kN/m3和0°。拱圈设计温度荷载见表2。按照抗震规范的要求，计算中依据坝址地震危险性分析得到相当于100年期限内超越概率为2%的拱坝坝址基岩水平设计地震加速度代表值为0.406g，竖向取为水平向的2/3，即为0.271g。根据设定地震场地相关反应谱拟合得到的人工地震波，其归一化后的图形见图6。

表2 正常水位温降工况下拱圈设计温度 （单位：℃）

3.2 坝址地震危险性分析高拱坝的坝址区域地震危险性分析见图7。大坝的设计地震和校核地震的水平向基岩峰值加速度分别为：设计地震100年超越概率2%的坝址区基岩水平地震峰值加速度代表值0.406g，校核地震100年超越概率1%的坝址区基岩设计地震峰值加速度代表值0.481g。由图7可知，在地震动强度范围内，地震危险性曲线采用直线来近似描述是可以接受的，即可采用式（3）、式（4）求得地震危险性分析参数K和K0：

3.3 高拱坝-地基体系整体稳定概率地震需求模型针对不考虑和考虑右岸坝肩接触面上的残余凝聚力（取值为峰值凝聚力的30%）两种模型，分别采用拉丁超立方抽样方法抽取了N=50 组不确定性参数摩擦系数和凝聚力的样本（参数均值及概率分布类型，见表1）作为输入参数。地震作用下，高拱坝坝肩抗滑稳定性不仅受拱推力的影响，还受到坝肩滑块惯性力的影响。根据Hariri等的研究［30］，当坝体的地震响应为重点关注对象时，结构基本周期对应的反应谱加速度可能是最佳的地震动强度参数IM。对于拱坝坝肩滑块地震抗滑稳定性，PGA可能是最具代表性的IM。因此，本文选取所生成的人工地震波地震峰值加速度PGA作为IM，并将其按照比例系数进行调幅，调幅后的峰值加速度逐渐增加，分别为0.1g，0.2g，0.3g，0.4g，0.5g，0.6g，0.7g，0.8g，0.9g，1.0g。由此，基于增量动力分析方法（IDA，incremental dynamic analysis）分别针对两种模型进行了500次非线性动力分析。

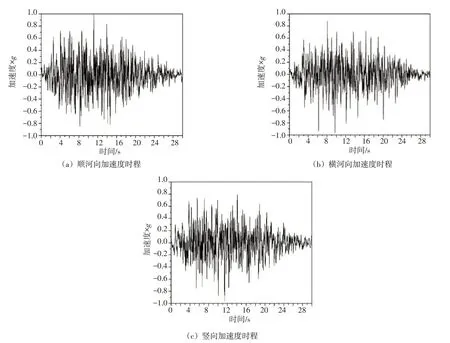
图6 归一化的人工地震波时程曲线

根据计算结果，将表征拱坝坝肩地震抗滑稳定性能的滑动面特征点的残余滑动位移与地震动强度峰值加速度指标按式（7）进行回归分析，分别构建了考虑与不考虑残余凝聚力的拱坝坝肩抗滑稳定性的概率地震需求模型（见图8）。其相应的拟合公式和相关参数，分别见式（25）和式（26）以及表3。由图8 以及表3 可知，考虑和不考虑残余凝聚力的拱坝坝肩稳定概率地震需求模型的对数标准差均很小，拟合判定系数R-Square均超过了0.95，表明回归分析的结果较好，所构建的概率地震需求模型能够精确地反映拱坝动力响应与地震动参数之间的关系。

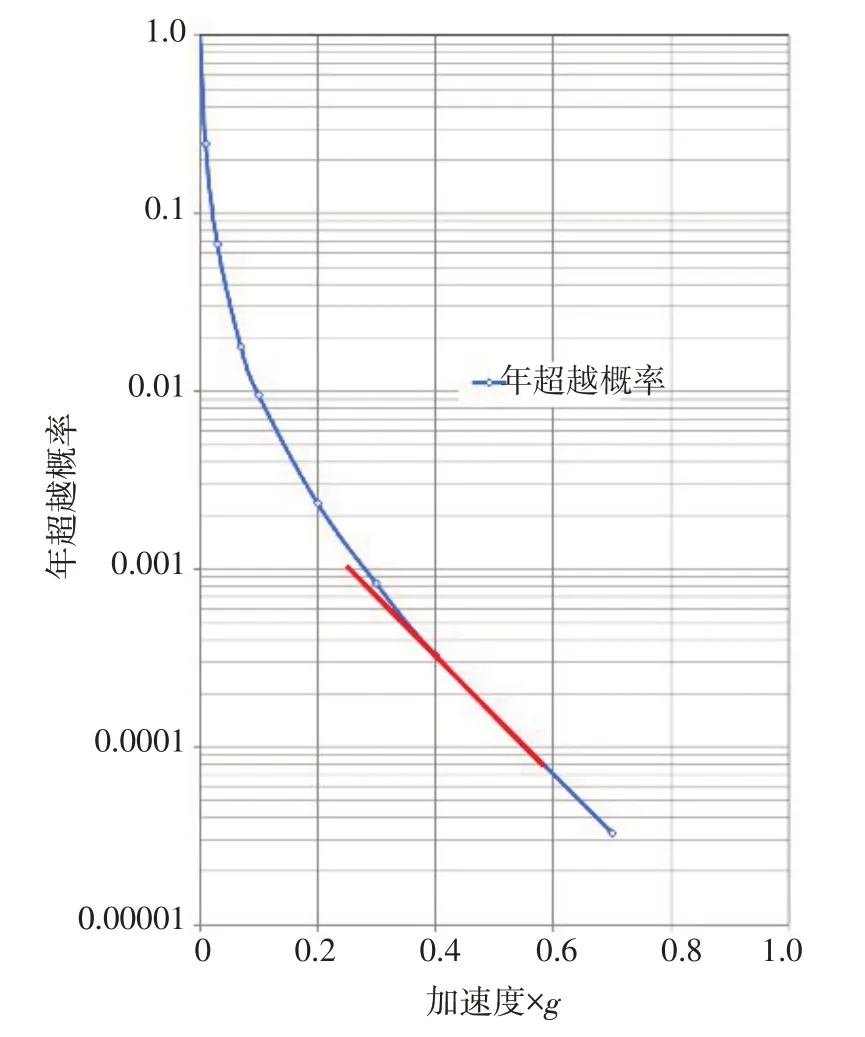
图7 地震危险性分析

由此可知，本文所选取的地震动峰值加速度可以作为高拱坝-地基体系地震整体抗滑稳定性分析中有效的地震动强度参数，接触面特征点残余滑动位移能够作为有效的性能指标。

不考虑接触面残余凝聚力：

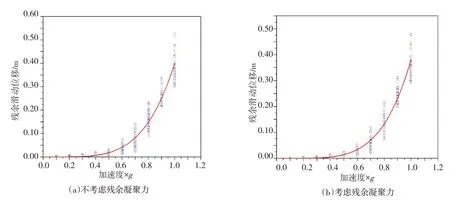
图8 拱坝坝肩稳定的概率地震需求模型

表3 考虑与不考虑残余凝聚力拱坝概率地震需求模型拟合系数

考虑接触面残余凝聚力：

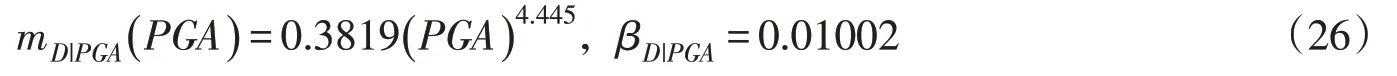
3.4 高拱坝-地基体系整体稳定地震易损性分析强震作用下拱坝-地基系统的整体失稳是包含各部分局部开裂和滑移在内的总变形逐步发展和累积的过程。本文采用增量动力分析方法，在地震动峰值加速度逐级增加情况下，文中右岸坝肩滑块的滑动及其带动坝体产生向下游的变形是造成拱坝-地基系统的整体失稳的主要原因。由此，依据非线性动力分析计算汇总所得的特征点残余滑动位移IDA曲线50%分位数和均值曲线，得到拱坝-地基体系地震整体稳定性能水平划分图。由图9可见，曲线被两个转折点分为三个阶段：（1）第一阶段。随着地震动的增加，右岸坝肩滑块仅发生轻微的滑动，特征点的残余滑动位移很小，几乎为0，表明拱坝地基系统稳定性能良好，处于稳定区域；（2）第二阶段。特征点的残余滑动位移随着地震动强度的增加而缓慢的增加，拱坝坝肩滑块虽发生了局部滑动，但最大残余位移小于0.04 m，大坝整体稳定性能尚处于可控范围内；（3）在第三阶段。特征点残余滑动位移迅速增长，拱坝地基系统稳定性处于不可控状态，已经发生了整体滑动失稳破坏。

由此，依据各个阶段转折点的出现可将拱坝-地基体系地震整体抗滑稳定两级性能水平及其对应的残余滑动位移阈值定义为：（1）局部滑动，对应于第一个转折点出现时的特征点残余滑动位移0 m，亦即特征点开始出现残余滑动位移；（2）整体滑动失稳破坏，对应于第二个转折点出现时的特征点残余滑动位移0.04 m。

基于所定义的性能水平，采用式（10）和式（11）计算可得不考虑和考虑残余凝聚力的混凝土拱坝-地基体系整体稳定地震易损性曲线见图10。

图9 基于残余滑动位移的混凝土拱坝-地基系统性能水平划分

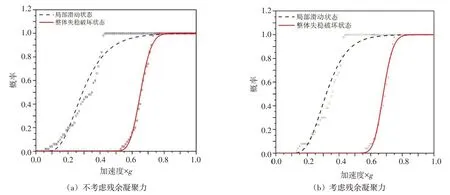
图10 不考虑和考虑残余凝聚力基于残余滑动位移的拱坝地震易损性曲线

图11 拱坝底滑面特征点残余滑动位移年超越概率

图12 考虑与不考虑拱坝底滑面特征点残余滑动位移年超越概率

3.5 高拱坝-地基体系整体稳定地震风险分析结合不考虑与考虑残余凝聚力的拱坝概率地震需求模型所得的参数a、b和βD|im（见表3）代入式（21）即可得到考虑与不考虑残余凝聚力，拱坝坝肩滑动岩体底滑面特征点残余滑动位移年超越概率曲线见图11和图12。依据式（21）求解出在设计年限内，拱坝-地基体系滑动稳定不同性能水平的概率见表4。

由表4可知，在设计基准期限范围内，考虑与不考虑残余凝聚力，该拱坝控制在局部滑动稳定性能水平的概率分别达到99.59%和99.65%，表明该拱坝在设计基准期内坝肩滑块发生相对明显滑动位移的概率较小。在设计基准期限内，考虑与不考虑残余凝聚力，坝肩滑块滑动面残余滑动位移超过0.04 m的概率分别为0.41%和0.35%，拱坝-地基体系发生整体滑动失稳破坏的可能性极小，且考虑残余凝聚力后拱坝-地基体系整体地震抗滑稳定性能有略微的加强。

表4 100年设计基准期内拱坝-地基体系地震抗滑稳定不同性能水平概率

4 结论

本文通过将概率地震需求模型、采用经典幂指数函数描述的地震危险性分析函数和混凝土坝地震易损性分析解析函数相结合，推求了地震危害性分析的解析函数，由此开展了高拱坝-地基体系整体稳定概率地震风险分析。主要成果如下：（1）对地震动强度与结构动力响应需求参数的关系，即结构的概率地震需求模型的数学描述进行了推导，在此基础上引入地震动强度与结构动力响应幂指数函数关系，以某高拱坝工程为实例，建立了综合考虑坝体横缝、坝肩滑块和坝基交界面接触非线性的高拱坝-地基体系有限元模型，在概率统计框架下，进行了一系列非线性动力分析，构建了高拱坝-地基体系整体稳定概率地震需求模型。（2）基于非线性动力分析结果，划分了高拱坝-地基体系整体抗震稳定两级性能水平，以坝肩右岸滑块底滑面特征点的残余滑动位移为性能指标，定义了相应的阈值，依据所定义的性能水平，开展了高拱坝-地基体系整体稳定地震易损性分析，构建了地震易损性分析模型，绘制了相应的地震易损性曲线，为后续开展概率地震风险分析提供基础。（3）引入幂指数的形式描述地震危险性曲线，结合概率地震需求模型和地震易损性曲线解析函数，推求了地震风险分析的解析函数，构建了高拱坝-地基体系整体稳定概率地震风险分析模型，并据此开展了考虑和不考虑右岸坝肩滑块接触面上残余凝聚力的高拱坝-地基体系整体稳定概率地震风险分析研究，给出了高拱坝-地基体系在设计基准期限内到达不同性能水平的年超越概率，为其在极限地震下的抗震安全评价提供了依据，同时为现有基于准则的混凝土坝抗震安全决策转向基于风险概率的安全决策提供科学依据。