考虑土体不排水强度非平稳性对条形基础承载力影响的可靠度分析

严柏杨，张京伍，朱德胜，葛 彬，舒 爽

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.东华理工大学 土木与建筑工程学院，江西 南昌 330013；3.扬州大学 建筑科学与工程学院，江苏 扬州 225009)

基础的极限承载力一直是岩土工程界关注的热点问题，国内外众多学者在基础的承载力方面运用数值方法[1-2]，实验方法[3-4]和理论方法[5-6]进行了深入研究，并且获得了丰硕的成果。然而，在这些研究中土体的参数都被考虑成确定性的。由于沉积和沉积后的过程，即使在均匀土层内，土体性质也会在空间上发生变化。土体性质的内在固有空间变异性是岩土工程不确定性的主要来源之一，对基础承载力有着重要的影响。近年来采用随机场理论来分析岩土工程相关问题已经越来越受到国内外学者的关注，例如陈朝晖等[7]分析了土的抗剪强度参数空间变异性对边坡稳定性的影响，并与三种典型极限平衡法进行了对比；Griffiths和Fenton[8]建立了二维情况下基础不均匀沉降的随机有限元模型，并分析了相关距离和变异系数对基础不均匀沉降的影响。在地基承载力方面，倪红等[9]结合工程实例分析了土性参数特性对地基承载力可靠度指标的影响规律；张春会等[10]研究了黏土粘聚力的变异系数对条形基础地基承载力的影响。然而这些研究没有考虑到土体参数随着深度线性增加的变异趋势。Li等[11]指出，使用土体不排水强度的平稳随机场不能准确地评估基础失效概率。在目前的文献中，鲜有非平稳随机场模型中基础极限承载力的分析。

本文以条形浅基础为例，探究土体不排水强度的非平稳性以及相关距离对极限承载力的影响。结合随机有限单元法与蒙特卡罗模拟，对条形基础的承载力和可靠性进行了分析，探讨了土体参数非平稳程度和相关距离对承载力随机响应的影响。从实际工程设计角度出发，给出了失效概率的变化规律和相应的安全系数取值。

1 随机场理论

本文以模拟土体不排水抗剪强度su的变异来分析极限承载力的随机响应问题。不排水抗剪强度的空间变异性一般用均值、变异系数和相关距离来表征。不排水抗剪强度的均值符合对数正态分布，并随着深度线性增长，满足如下关系：

su=su0+kz

(1)

式(1)中su0为土体表面的不排水抗剪强度，k和z分别为非平稳系数和深度。su0的典型值在 0到10 kPa之间，k的取值范围在0～3.5 kPa/m之间[12]。变异系数的建议值在10%～50%之间。目前文献中对不排水抗剪强度相关距离的阐述较少，本文选取各向同性的相关距离进行研究，采用的分析参数具体见表1。

表1 随机场模拟参数

2 随机有限元模型

使用有限元软件Abaqus 6.14版本在二维平面应变条件下建模并进行极限承载力的分析。如图1所示，假设条形基础为粗糙刚体，置于土层上部，宽度B=10 m，高度H=1 m。条形基础与土的接触面使用软件中的“tie”类型进行约束，确保基础与土体之间无相对位移。土体本构模型采用线性-弹性完全塑性本构模型，采用Tresca破坏准则。弹性响应由杨氏模量和泊松比定义，杨氏模量与不排水抗剪强度满足关系E=500su，这样既不影响计算结果的准确性，同时又可以提高计算效率；泊松比设置为0.495，以模拟无体积变化的不排水条件。

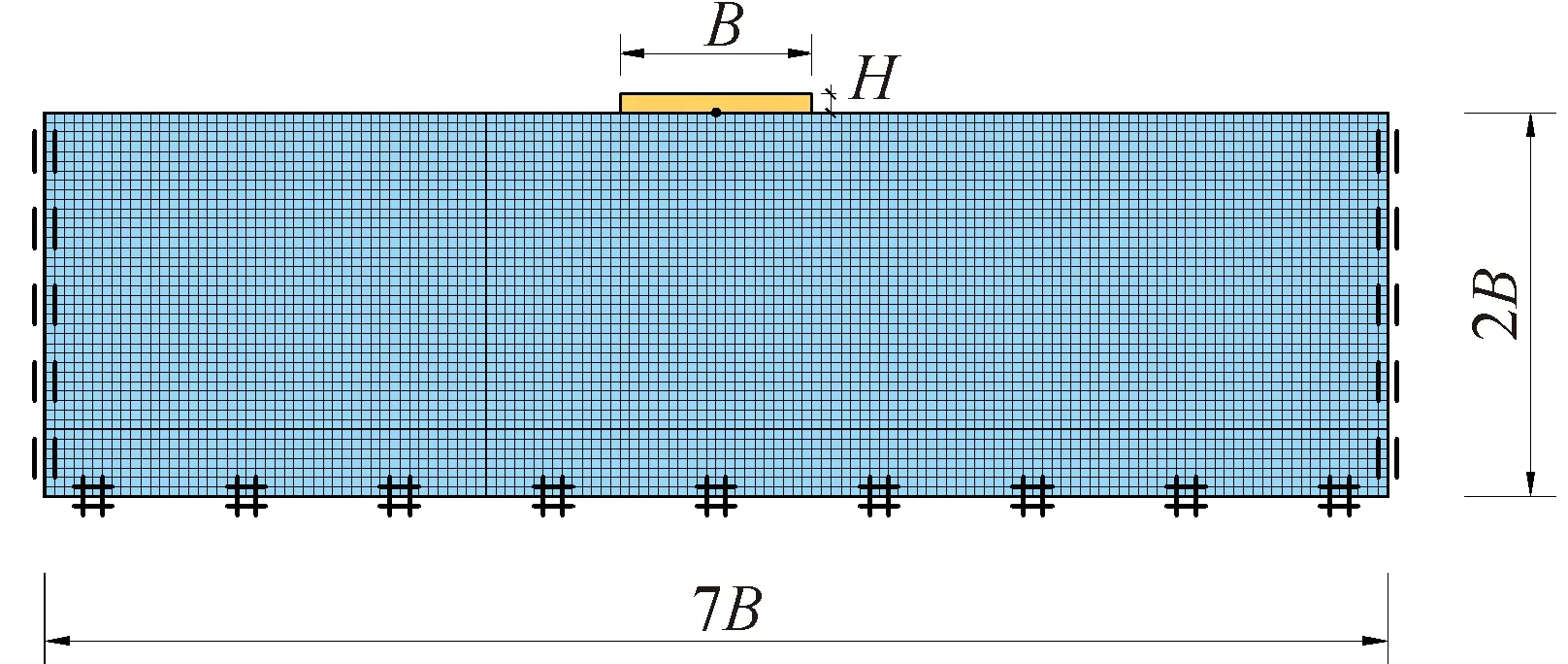
图1 有限元模型Fig.1 Finite element model

土体区域模型高度为20 m (2B)，宽度为70 m (7B)，可以确保无明显的边界效应产生。土体左右边界被限制水平位移，下部边界的水平和竖向位移被同时限定。依据Der Kiureghian和Ke[13]的研究结果，为了在随机有限元分析中保证结果的准确性，网格的尺寸不应超过水平或竖直相关距离的0.5倍。本文考虑的最小相关距离为1 m，因此网格尺寸设定为0.5 m×0.5 m，类型为四结点双线性平面应变减缩积分四边形单元。

以确定性情况下su=10 kPa为例来验证有限元模型的合理性。根据传统的承载力系数定义Nc=q/su0(q为计算得到的极限承载力)，本文模型的结果为5.37，比Prandlt解Nc=5.14高出了约4%。与Cassidy等[14]的数值解Nc=5.28相比高出了约1.6%，这主要是由于本文比较粗糙的网格划分导致的，进一步细化网格可以使结果更加接近于Prandtl解析解和Cassidy等[14]的数值解。

3 结果与讨论

蒙特卡罗模拟的次数对随机场结果的精度有很大的影响，为了获得较好的计算精度，本文所有工况采用500次蒙特卡罗模拟。图2以工况k=0，L=1 m为例，展示了承载力系数随机响应的均值与方差随着蒙特卡罗模拟次数变化的规律。可以看出随着模拟次数的增加，承载力的均值与方差约在第350次模拟时基本趋于平缓，由此可见本文采用的500次蒙特卡罗模拟完全可以获得良好的随机响应精度。

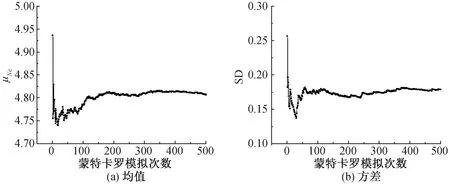
图2 k=0，L=1 m工况下蒙特卡罗模拟次数对承载力的影响Fig.2 The effect of Monte Carlo simulations on bearing capacity when k=0，L=1 m

图3展现了不同相关距离对基础承载力系数的影响。图片纵轴为承载力系数，即承载力均值与之相对的确定性结果归一化之后的结果，可以看出当引入随机场进行分析后这些值均小于1。随着相关距离的增大，承载力系数先减小再增大。对于不同非平稳程度，最小值均出现在L=10 m处，即相关距离与基础宽度相等，这与Griffiths等[8]的结果一致。相关距离较大时，土体参数局部平均效应的影响减弱，使得承载力得到了显著提升。

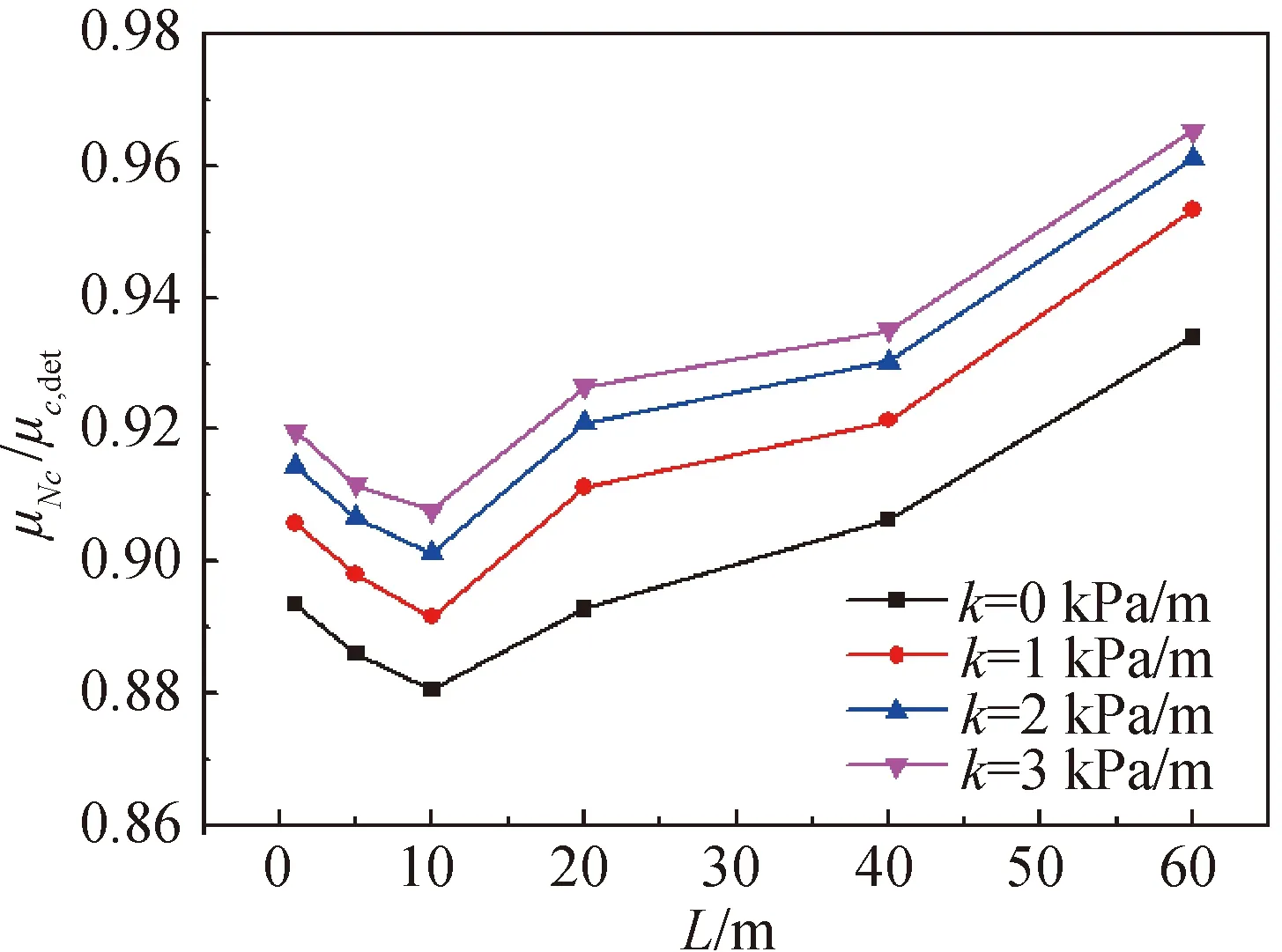
图3 相关距离对基础承载力系数的影响Fig.3 The effect of spatial correlation length on the foundation bearing capacity factor

不同非平稳程度对基础承载力的影响见图4。承载力系数与非平稳程度呈现正相关趋势，土体不排水强度非平稳程度越高，承载力系数越大。这是由于基础下方土体的强度随着非平稳程度的提高而增大，导致了极限承载力的增加。

图4 非平稳程度对基础承载力系数的影响Fig.4 The effect of degree of non-stationarity on the foundation bearing capacity factor

承载力标准差(SD)随着相关距离的变化如图5所示。可以看出在相关距离较小时，标准差几乎随着相关距离的增加而线性增加；对于较大的相关距离，曲线变得逐渐平缓，增长幅度明显减小。非平稳程度系数对标准差的影响也是十分显著的，相同的相关距离下，非平稳程度系数越大，标准差越大。主要原因是相关距离较小时，土体的不排水抗剪强度在较小的区域内波动剧烈，局部平均效应变得显著，导致承载力的标准差较低；相反，当相关距离较大时，基础下方土体可能出现较大区域的高强度土体或低强度土体，使得承载力的标准差变大。

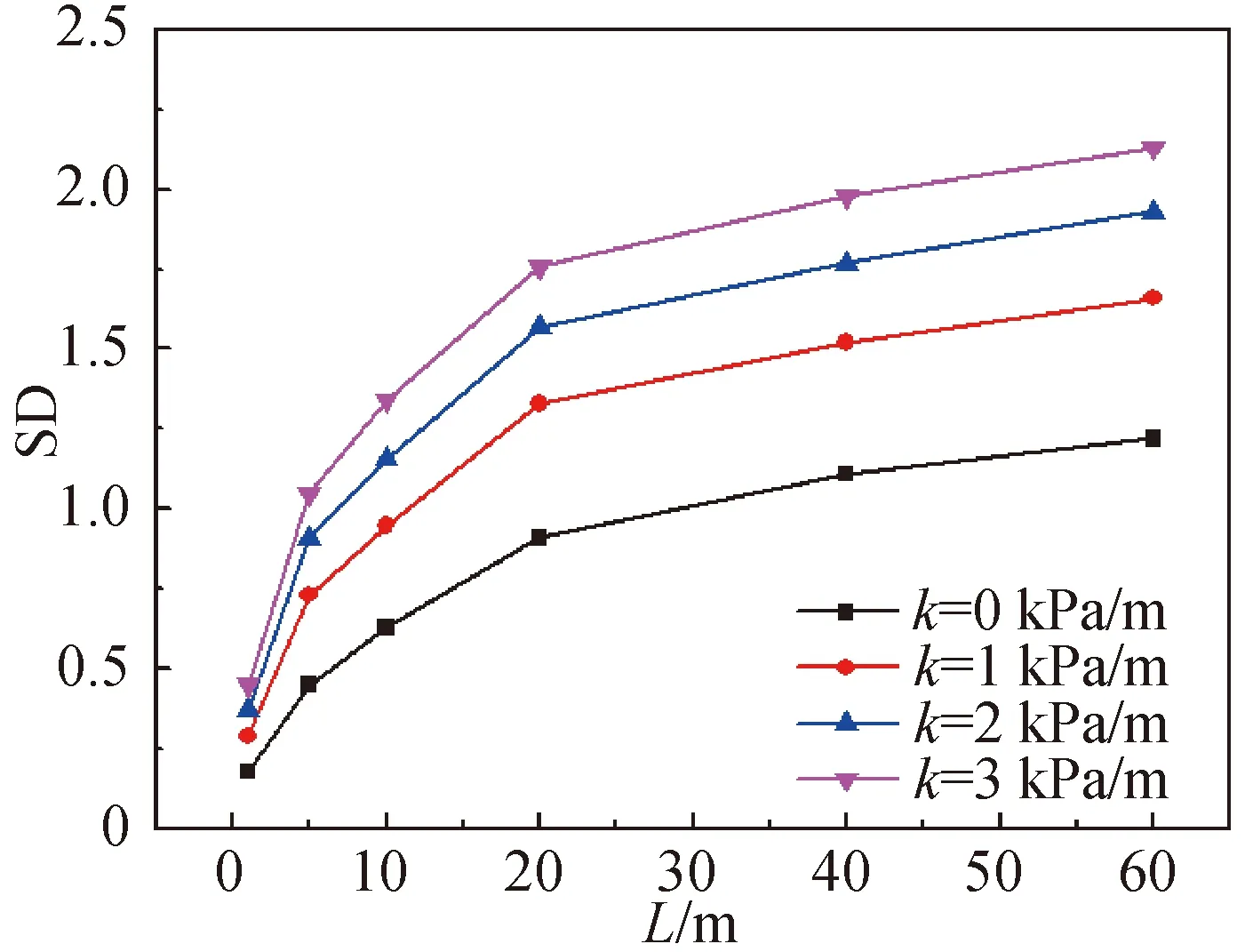
图5 承载力标准差与相关距离之间的变化规律Fig.5 The relation between the standard deviation of bearing capacity and spatial correlation length

图6 L=1 m时典型破坏面云图Fig.6 Typical failure plane contours when L=1 m

图7 k=1 kPa/m时典型破坏面云图Fig.7 Typical failure plane contours when k=1 kPa/m

图6为相关距离L=1 m时的典型破坏面云图。为了使破坏面具有可比性，所有随机有限元实现中的随机场均来源于相同的基准场，即相同的随机模式但是不同的数值。比较图6中的四幅破坏面云图可以看出：随着非平稳程度的不断提高，破坏面的长度在不断减小，同时土体受影响区域面积也逐渐减小。以往研究表明，破坏面的长度、数量和破坏面穿过土体的强度与基础承载力有着密切的联系。虽然在k=3 kPa/m时破坏面长度最短，但是仍然拥有最高的承载力。

在同一非平稳程度下，不同相关距离对破坏面的影响见图7。可以看出，随着相关距离变大，总体上破坏面的长度和数量也在增加。虽然图7(a)中的破坏面长度相比其他三幅图要长，但是由于受局部平均效应的影响，基础下部软弱土层较多，使得其承载力与其他相关距离下相比较小。

图8给出了k=1 kPa/m，L分别等于5和40 m时的承载力系数概率分布函数(PDF)。基于卡方拟合优度检验，可以用正态分布函数来表征所有相关情况下的分布。值得注意的是，L较小时的PDF曲线分布要比较大L时的PDF曲线窄。这种现象是可以预料到的，因为随着相关距离的增加，承载力因子的COV逐渐增大。

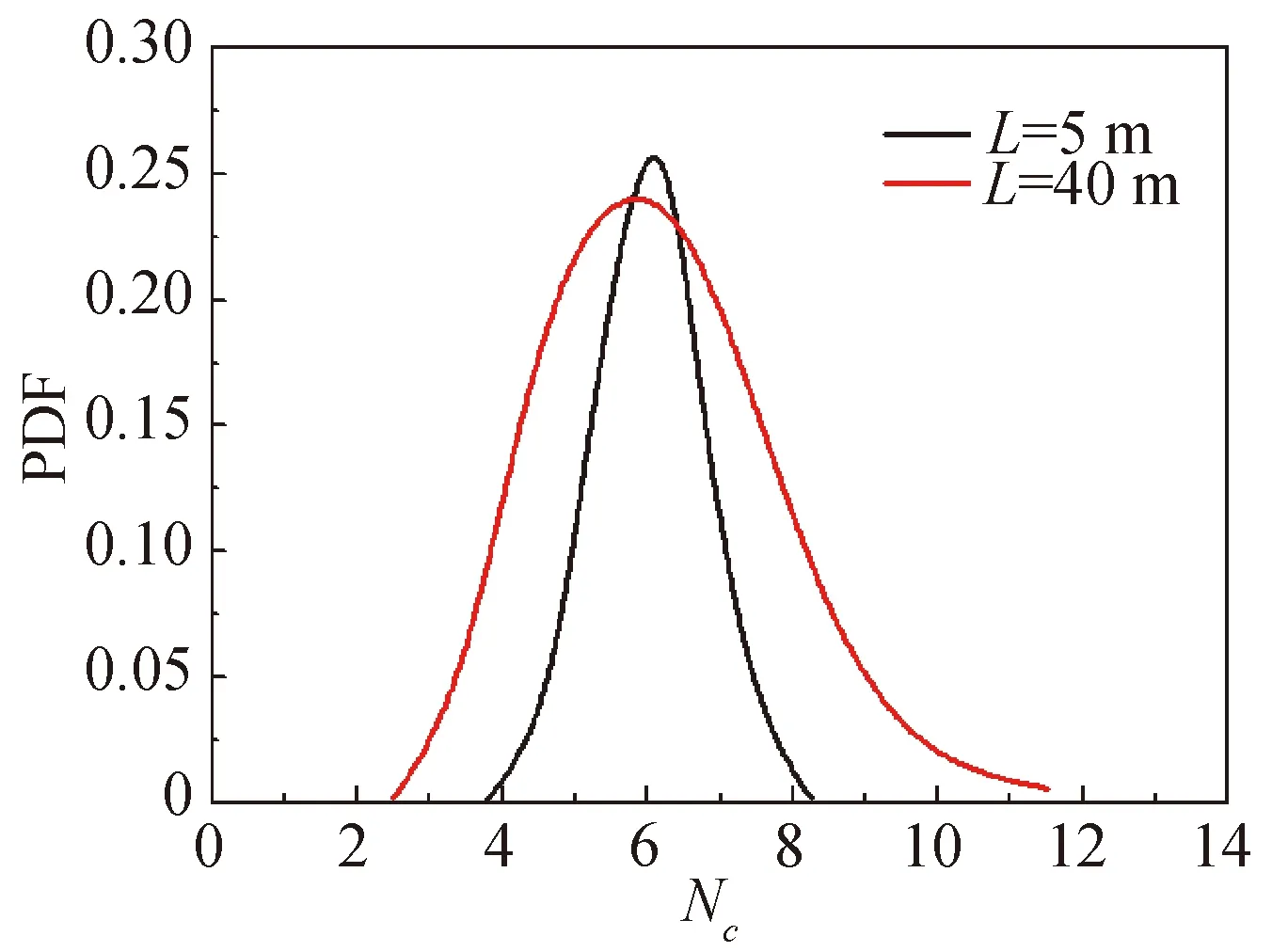
图8 k=1 kPa/m时的承载力系数概率分布函数(PDF)Fig.8 The probability distribution function of bearing capacity factor under the condition of k=1 kPa/m

在传统的基础设计中，极限承载力是用不排水抗剪强度的平均值来计算的，而许用荷载是通过引入全局安全系数(FS)来计算的。通过引入安全系数的概念，当承载力系数服从正态分布时，其破坏概率可计算为:

(2)

式中，Φ为对数正态累积分布函数；λNc和ξNc分别是取对数后承载力系数的平均值和标准差。

图9给出了不同安全系数下失效概率随着相关距离变化的规律。对比三张图可以看出，随着安全系数的增加，失效概率不断地减小。在相同安全系数下，当L在1到40 m之间时，失效概率不断增大；当L大于40 m时，失效概率趋于平缓。

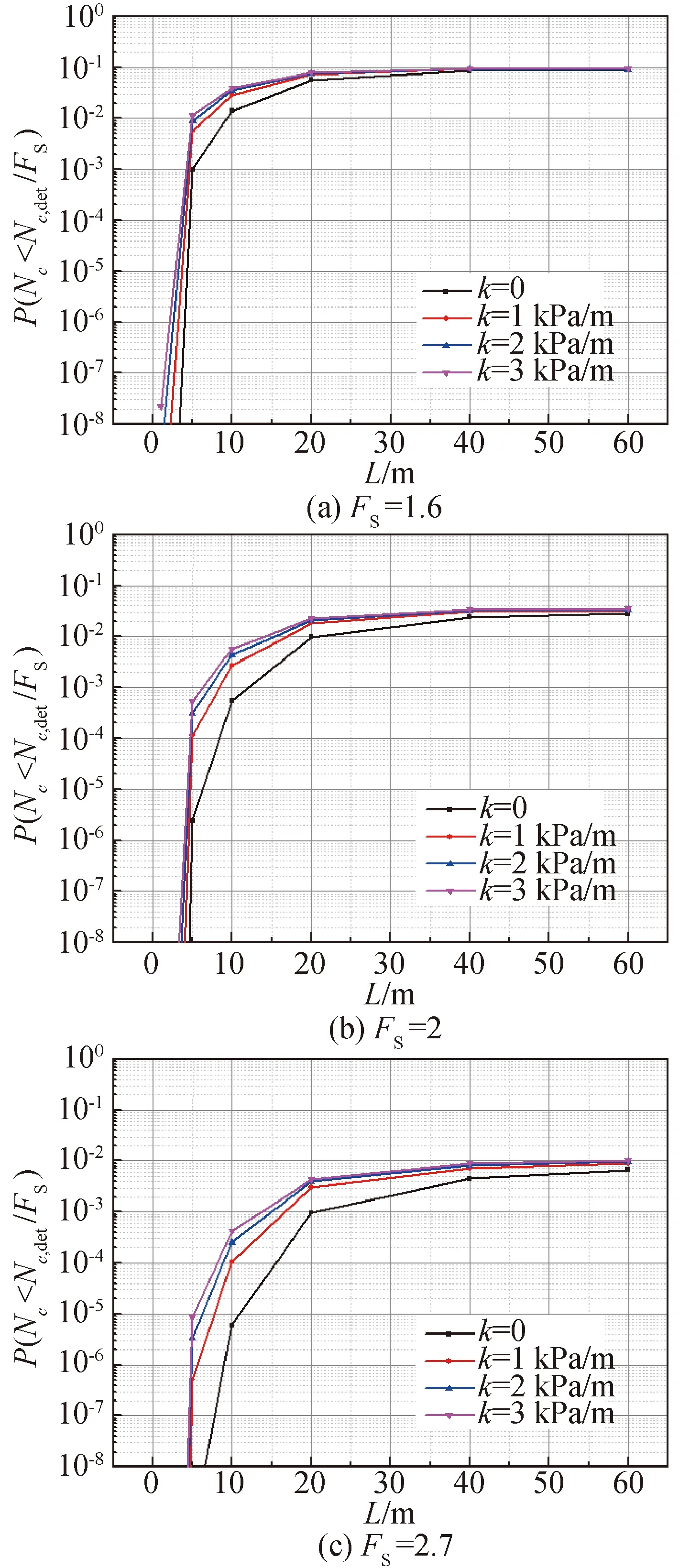
图9 失效概率随相关距离变化规律Fig.9 The relation between the probability of failure and spatial correlation length

不同非平稳程度对失效概率的影响见图10。可以看出随着非平稳程度的提高，基础的失效概率在逐渐增大。工程中一般要求将基础的失效概率控制在10-3至10-2之间，当FS=2.7时，即可满足工程设计要求。

图10 失效概率随非平稳程度变化规律Fig.10 The relation between the probability of failure and degree of non-stationarity

4 结论

1)土体参数的非平稳性和相关距离对基础的承载力影响显著。随着非平稳程度的提高，基础的承载力逐渐增大。在相关距离小于基础宽度时，承载力逐渐减小，当相关距离大于基础宽度时，承载力随着相关距离的变大而变大。

2)总体来说，非平稳程度较大时，破坏面数量较少，分布较浅；相关距离越大，破坏面分布变广，破坏面的数量也相应增加。

3)基础的失效概率与非平稳程度和相关距离成正相关的关系。在本文考虑的参数范围内基础设计选取安全系数等于2.7可以满足设计要求。