基于神经网络模糊PID控制的无刷直流电机控制系统研究
贾贇贺 张昕 周媛媛
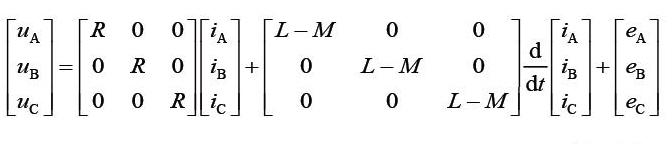

摘 要:针对电动汽车行驶工况的要求,为了使电机能够有良好的启动特性和稳态特性,在Simulink中建立了无刷直流电机转速-电流双闭环控制系统仿真模型,转速控制神经网络和模糊控制对PID控制参数进行在线整定;电流环采用电流滞环控制,并对控制模型进行空载启动后加载实验。实验结果表明,本文设计的控制系统响应速度快,无静差,抗干扰能力强。
关键词:无刷直流电机 神经网络 模糊控制
无刷直流电机因为振动噪声小、功率密度大和启动性能好等优点,在电动汽车领域有着很好的应用前景。前人对无刷直流电机控制的研究做了很多工作,刘成强等人[1]将无刷直流电机控制系统的转速环和电流环都采用PI调节器,虽然系统的响应速度快,但是电机转速会出现超调现象,同时也会有较大的转矩脉动。朱明祥等人[2]将矢量控制应用于无刷直流电机控制,采用模糊控制进行调速,该方法可以降低转矩波动。张立伟等人[3]将霍尔开关与矢量控制相结合,解决了无刷直流电机在工作时噪声等问题。Faradja等人[4]提出了无刷直流电机混沌系统的广义哈密顿函数,应用该函数的电机可以识别不同的动力模式。
本文设计了基于转速-电流双闭环控制的电机控制器。在Simulink中建立了仿真模型,根据电动汽车电机的工作环境进行仿真试验,验证该控制器的可靠性。
1 无刷直流电机模型建立
将电机视为理想电机,且满足下列条件:(1)气隙磁场的分布形式为梯形分布;(2)定子齿槽的影响忽略不计;(3)电枢反应对气隙磁通的影响忽略不计;(4)忽略电动机中的磁滞和涡流损耗;(5)三相绕组完全对称。
无刷直流电机的三相电压方程为:
(1.1)
由于电机定子绕组的中性点是在理论分析中假想的,实际中的各相电压在测量时有很大的难度。为了便于和实际物理模型进行连接,可以使用基于线电压的数学模型。将三相电压方程两两相减就可以得到线电压方程,如式所示。
(1.2)
电机的电磁转矩方程为
(1.3)
无刷直流电机的运动方程为
(1.4)
2 无刷直流电机控制系统建模
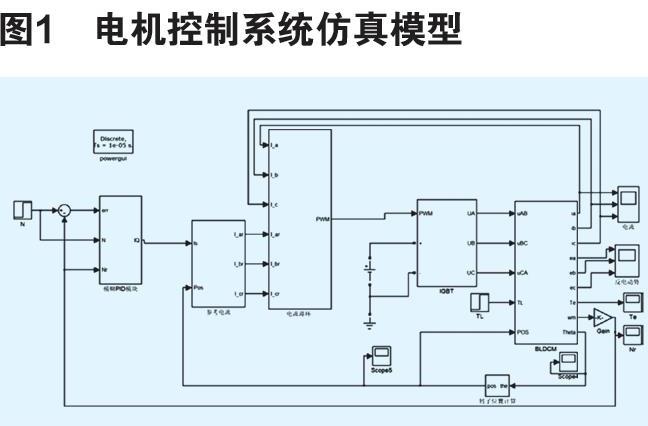
根据上一章无刷直流电机数学模型的分析,在Simulink中建立无刷直流电机控制系统仿真模型,如图1所示。
2.1 转速控制系统设计
控制系统采用转速-电流双闭环控制,转速控制器采用神经网络和模糊控制对PID参数在线整定,其原理如图2所示。
本文中的模糊控制器采用多变量二维的形式,两个输入分别为转速误差E和误差变化率EC,控制器的输出量为PID控制系数的补偿量ΔKp、ΔKi、ΔKd,如图3所示。
输入和输出的模糊子集为{负大,负中,负小,零,正小,正中,正大}。誤差E的论域为[-6,6],误差变化率EC的论域为[-10,10]。PID控制系数的补偿量ΔKp、ΔKi、ΔKd的论域均为[-3,3]。模糊控制器的输入和输出的隶属度函数均采用三角形函数,构建相应的模糊规则,如表1所示。
同时本文采用基于RBF网络对PID控制参数在线整定。该算法由经过训练的RBF神经网络选择PID控制参数。
采用增量式PID控制器,控制误差为:
error(k)=rin(k)-yout(k)(1.5)
PID控制器的三项输入参数为:
(1.6)
控制器采用的控制算法为:
u(k)=u(k-1)+Δu(k) (1.7)
Δu(k)=kp(error(k)-error(k-1))+kierror(k)+kd(error(k)-2error(k-1))+error(k-2) (1.8)
神经网络的整定指标为
E(k)=error(k)2(1.9)
kp、ki和kd的调整方法采用下降梯度法:
(1.10)
式中,为被控对象的Jacobian信息。基于径向基神经网络PID控制器的雅可比矩阵为:
(1.11)
根据上文对神经网络PID控制的分析,径向基神经网络的核心部分是有S函数来实现,将S函数的更新函数设置为PID控制函数。
2.2 电流控制设计
电流环采用电流滞环控制,其原理如图4所示,输出为6路PWM信号。为了能使电机实际的输出电流更加符合参考电流的波形,就需要将电流滞环中的阈值设置为合理值,本文选取环宽限值为±0.05。
参考电流随着转子位置的改变发生变化,将转子位置的一个周期2π平均分为6份,每份转角为π/3,在Simulink中使用S函数来实现表2所示的关系。本文中的转子位置检测采用rem()函数来实现。
逆变器模块采用Simscape中的Universal Bridge模块,把功率电子元件设置为IGBT,根据电流滞环输出的PWM信号,判断逆变器开关的时机,从而输出电压。由于本文采用线电压方程对电机建模,所以逆变器也需要输出线电压。
3 仿真分析
本文中,电机的参数设置为:定子绕组电阻R=2.875Ω,定子等效电感L-M=8.5×10-3H,转动惯量J=0.008kg·m2,黏滞摩擦系数BV=0.001N·m·s/rad,供电电压Udc=220V,极对数np=4,额定转速N=1200r/min。速度环控制初始参数为kp=30,ki=10,kd=0.1。
将无刷直流电机空载启动,给定转速为n=1200r/min。在运行到0.4s时,突然施加2.5N·m的机械负载。电机的输出转速、电磁转矩、反电动势以及三相电流的波形如图5~图8所示。
由图5所示的电机输出转速图可以看出,在电机启动阶段,电机的输出转速迅速响应,而此时的电磁转矩迅速升高到3.2N·m。当电机达到给定转速时,电机的三相电流非常小,电磁转矩也降至0.25N·m,这是因为在系统运行时产生的摩擦转矩。根据无刷直流电机运动方程分析可知,因为电机处于稳定状态,此时电磁转矩和机械负载转矩的差值的计算公式为:
(1.12)
计算可得到转矩差是0.252N·m,可以看出在空载启动阶段的仿真结果与电机运动方程一致。此时反电动势波形也稳定为梯形波,与理论波形相符。
当电机负载突增时,转速突然下降,并在极短地时间内恢复到目标转速,此时电机的转矩在短时间内迅速升高,最后稳定在2.7N·m左右,这是因为电机的电流增大使得电磁转矩也增大,以此来平衡负载转矩。
4 结语
本文设计了转速基于RBF神经网络的模糊PID控制、电流采用电流滞环控制的双闭环控制系统,同时基于该控制系统在Simulink中建立了无刷直流电机控制系统仿真模型,并进行仿真实验。仿真结果表明,本文设计的无刷直流电机控制系统的转速和转矩响应快速,对于系统扰动具有良好的抗性。
参考文献:
[1]刘成强,徐海港.纯电动车驱动电机控制系统建模与仿真研究[J].机械设计与制造,2018(S1):107-109+113.
[2]朱明祥,孙红艳,慈文彦,窦爱玉,袁丽丽.一种改善BLDCM调速性能的模糊矢量控制策略[J].电测与仪表,2018,55(21):132-137+142.
[3]张立伟,毛学宇.基于电动汽车的无刷直流电机低扭矩脉动混合矢量驱动控制[J].电工技术学报,2015,30(S2):71-81.
[4]Philippe Faradja,Guoyuan Qi. Hamiltonian-Based Energy Analysis for Brushless DC Motor Chaotic System[J]. International Journal of Bifurcation and Chaos,2020,30(08).

