基于曲波变换的航空电磁数据调平方法研究

高玲琦， 殷长春* ， 王宁， 刘云鹤， 苏扬， 熊彬

1 吉林大学地球探测科学与技术学院， 长春 130026 2 桂林理工大学地球科学学院， 桂林 541006

0 引言

航空电磁法是基于直升机、固定翼飞机等移动搭载平台的地球物理方法.它利用不接地回线进行电磁发射并通过磁传感器接收电磁信号，实现对地下目体的探测.航空电磁具有效率高、成本低的特点，特别适合高山、沙漠、湖泊沼泽、森林覆盖等地形地质条件复杂地区的资源探测.目前航空电磁法已在矿产资源、地下水和地热、环境工程、城市地下空间、地质灾害监测等领域发挥了重要的作用(Reed，1981；Wolfgram and Golden，2001；Haas，2004；Smith et al.，2006；Viezzoli et al.，2010；Wiederhold et al.，2010；Minsley et al.，2012).

由于采用飞机平台搭载电磁设备，航空电磁数据中会产生很多地面电磁法遇不到的噪声和误差.最典型包括由飞机飞行状态不同导致电磁系统发生变化，从而产生的调平误差.调平误差与随机噪声存在本质区别，调平误差存在特定的物理成因，不具随机性，因此需要采取特殊方法对其进行处理.Huang和Fraser(1999)将调平误差分为测区调平误差、测线调平误差以及短波长调平误差.测区调平误差主要由不同架次之间电磁系统物理条件变化引起，在数据中表现为区块状的异常抬升.测线调平误差是由不同测线间由于温度、压力、风速和风向等条件发生变化，导致仪器状态发生变化而产生的(Huang，2008；Beiki et al.，2010；Siemon,2009).航空电磁(特别是直升机航空电磁)通常采用相邻测线来回飞行的“S”形观测方式，因此某一条测线上电磁系统面向太阳(或者迎风)，相邻测线上则背对太阳(或者避风)，造成相邻测线间系统状态发生变化，进而在电磁信号中产生条带状调平误差(称为窗帘效应).另外，由仪器噪声、飞行速度突然改变及局部热变化等因素还可引起短波长调平误差，在数据中表现为局部干扰(Huang，2008).

航空电磁数据调平旨在消除调平误差，改善数据质量.传统的位场数据调平大多基于位场随高度变化缓慢的特点，采用切割线调平(Yarger et al.，1978；Bandy et al.，1990；Minty，1991；Luyendyk，1997；Ferraccioli et al.，1998).然而，航空电磁信号对飞行高度非常敏感，在切割线与测线交叉处，难以保证飞行高度一致，因此切割线调平无法进行电磁数据调平.Huang和Fraser(1999)提出了一种针对视电阻率数据的自动调平方法.该方法通过一维与二维数据非线性相关滤波器的组合实现数据调平.Fedi和Florio(2003)提出了一种基于小波变换的调平技术，然而该方法受到小波变换仅有三个方向特征的限制.Mauring和Kihle(2006)提出了基于移动微分中值滤波器的调平方法，该方法可以应用于非平行分布的测线数据调平.Huang(2008)提出了基于测线数据相关性的调平方法.该方法基于相邻测线间信号具有较大的相关性，而调平误差不具有相关性的特点，通过最小二乘拟合相邻测线的数据差，实现航空电磁数据调平.Beiki等(2010)提出了基于一维和二维滑动窗口多项式拟合的航空电磁和航空磁测数据调平方法.Zhang等(2018)提出了基于主成分分析的调平方法并将其应用于航空电磁数据与航磁数据的调平.然而，上述方法均存在一定的局限性.其中，基于一维及二维滤波的调平方法本质上对数据整体进行了平滑处理，容易导致高频细节的丢失，而基于误差多项式拟合的方法由于其阶数限制，常常不能完美地拟合误差，造成调平过度或残余.

为改善上述方法的局限性，本文提出一种基于曲波变换的调平方法，通过曲波变换的多尺度和多方向特征，调平误差得以在特定尺度和方向内被精确拟合并去除，从而避免多项式在拟合误差时的不准确性.另一方面，由于大多数尺度及方向未经调平处理，故数据畸变小，且不容易导致高频细节的丢失.在曲波变换等多尺度分析方法中，阈值法通过对曲波系数设置阈值实现数据去噪和数据重构等.Donoho和Johnstone(1994)首先提出了用于小波变换重构的硬阈值方法，之后，Donoho(1995)又提出了一种用于噪声去除的软阈值方法.目前两种方法均获得广泛应用.本文实现航空电磁数据调平，我们首先对飞行高度进行归一化处理(Huang，2008)，在此基础上对数据进行多尺度分析，通过设置阈值进行方向滤波有效去除数据中的调平误差.这种新调平方法与基于曲波变换数据去噪的不同之处在于：数据去噪仅需对信号进行多尺度分析，通过对高阶尺度设置阈值即可去除随机噪声(王宁等，2020)；然而，调平误差具有方向性，但不具有随机性，因此需要在特定方向和尺度上对其进行识别，进而通过设置阈值法去除调平误差.下面我们首先介绍曲波变换及其多尺度和多方向性，进而通过对调平误差进行分析，讨论如何通过在不同尺度和不同方向上设置阈值对调平误差进行去除.最后，我们通过对合成数据以及爱尔兰Waterford地区频率域航空电磁数据的调平验证本文调平方法的有效性.

1 基于曲波变换的数据调平方法

1.1 曲波变换

曲波变换是在小波变换基础上发展而来，同时继承了小波变换的多尺度性质.除此之外，曲波变换还具有多方向性，这使得我们能够利用曲波变换更好地表征二维或更高维的信号.本文将利用这些曲波变换特性实现航空电磁数据调平.为了方便理解，我们将首先介绍曲波变换的基本理论和离散算法.由于航空电磁数据是离散的，我们主要描述离散形式的曲波变换.

1.1.1 波数域中的笛卡尔窗函数

在二维波数域中，离散曲波变换通过笛卡尔窗函数平滑地提取不同尺度和不同方向上的数据信息(Candès et al.，2006).笛卡尔窗函数由径向窗与角度窗一起共同构建.其中，径向窗是一系列同心的正方形，可定义为

(1)

(2)

其中，ω=(ω1,ω2)为二维波数域中的变量，j为尺度参数，Φ由两个一维低通滤波窗口的乘积定义，即：

Φj(ω1,ω2)=φ(2-jω1)φ(2-jω2)，

(3)

二维波数域是由所有径向窗支撑而成，因此：

(4)

离散曲波变换中的角度窗Vj(ω)呈放射状，可定义为

Vj(ω)=V(2⎣j/2_|ω2/ω1),

(5)

其中，|_j/2_|表示对j/2取整.在对径向窗与角度窗分别进行定义后，离散曲波变换的笛卡尔窗函数可表示为

(6)

进而，我们引入等间隔的斜率：tanθl∶=l·2-⎣j/2_|,l=-2-⎣j/2_|,…,2⎣j/2_|-1，则(6)式可表示为

(7)

其中，剪切矩阵Sθ可表示为

(8)

图1 离散曲波变换定义的楔形窗(参考Ying et al.，2005)Fig.1 Wedge-shaped window defined by discrete curvelet transform (Refer to Ying et al., 2005)

图1展示了二维波数域中的窗函数.其中，最内层代表粗尺度.该尺度内的曲波不具有方向性(相当于小波).在粗尺度之外，径向窗呈同心的正方形状，而角度窗呈图中虚线所示的放射状.图中灰色的楔形区域由径向窗与角度窗共同支撑，它包含了特定尺度和方向上的数据信息.

1.1.2 空间域中的曲波函数

离散曲波函数为连续曲波函数的近似，它保留了连续曲波函数的所有性质(Ying et al.，2005).为了介绍离散曲波函数，我们首先定义连续曲波函数.在连续曲波变换理论中，母曲波φj(x)由楔形窗的逆傅里叶变换得到，进而所有尺度为2-j的曲波均可由母曲波经位移和旋转得到(Candès et al.，2006).

(9)

其中，x=(x1,x2)为空间域自变量，旋转矩阵定义为

(10)

由上面的讨论，我们可以通过二维信号与曲波函数的内积计算曲波系数，即：

(11)

通过二维傅里叶变换，我们也可以在波数域中计算曲波系数，即：

(12)

其中，Uj为连续曲波变换中的窗函数，可由φj的傅里叶变换得到.

在定义了连续曲波函数后，我们可以利用与(9)式相似的形式定义离散曲波函数：

(13)

其中，b为离散变量，可表示为

(14)

图2展示了四个不同的曲波函数与其对应的楔形窗.图2a中，空间域内的曲波函数由不同颜色的椭圆标记.其中，绿色代表第2尺度内的曲波函数，蓝色代表第3尺度的曲波函数，而红色和黄色代表第4尺度内不同方向的曲波函数.图2b中展示了波数域中对应的楔形窗.由图可以看出，随着尺度参数j增加，对应的曲波函数变小，其各向异性增强.值得注意的是，由于二维傅里叶变换存在90°的旋转关系，空间域内的曲波函数与波数域内的窗函数在方向上互相正交.

图3展示曲波函数在两个互相垂直的方向上的分布特征.沿主轴方向，其波形从中心向两侧缓慢衰减，而在垂直于主轴方向，其波形从中心向两侧呈现快速震荡衰减.此外，曲波函数波形的长度与宽度还满足如下各向异性尺度关系：

(15)

曲波变换的各向异性特征使得其能更好地表示不同方向上的特征.这种特征非常适合于航空电磁数据中测线误差调平.

1.1.3 基于Wrapping算法的离散曲波变换

Candès等(2006)提出了用于快速离散曲波变换的卷绕(Wrapping)和USFFT算法.本文中我们采用卷绕算法.(13)式中我们已经定义了离散曲波函数，我们采取与(12)式类似的形式在波数域中计算曲波系数，即：

(16)

式(16)经离散化可得：

(17)

必须指出，由于楔形区域无法直接进行傅里叶变换，利用式(17)进行离散曲波变换存在难度.为了解决此问题，我们在图4给出“Wrapping”算法的实施步骤.图4中高度为L1j、宽度为L2j黑色平行四边形为波数域中楔形的支撑空间，该空间内包含的信息由灰色椭圆形区域表示.为进行二维傅里叶变换，我们定义一个围绕坐标原点、边长分别为L1j和L2j的正四边形，并将包含在黑色平行四边形中的数据信息Wrapping到围绕原点的正四边形中，从而可进行二维傅里叶变换.

图2 空间域与波数域中的曲波(a) 空间域中四个不同的曲波函数； (b) 波数域中对应的楔形支撑空间(参考Herrmann and Hennenfent, 2008).Fig.2 Curvelets in spatial and wavenumber domains(a) Four different curvelets in spatial domain; (b) Wedge-shaped support in wavenumber domain(Refer to Herrmann and Hennenfent, 2008).

图3 不同方向曲波函数波形(a) 沿主轴方向； (b) 垂直于主轴方向.Fig.3 Curvelet waveforms in varied directions(a) Along the major axis; (b) Perpendicular to the minor axis.

Wrapping算法可归纳为如下4个步骤：

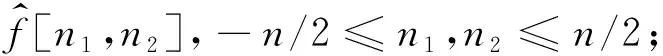
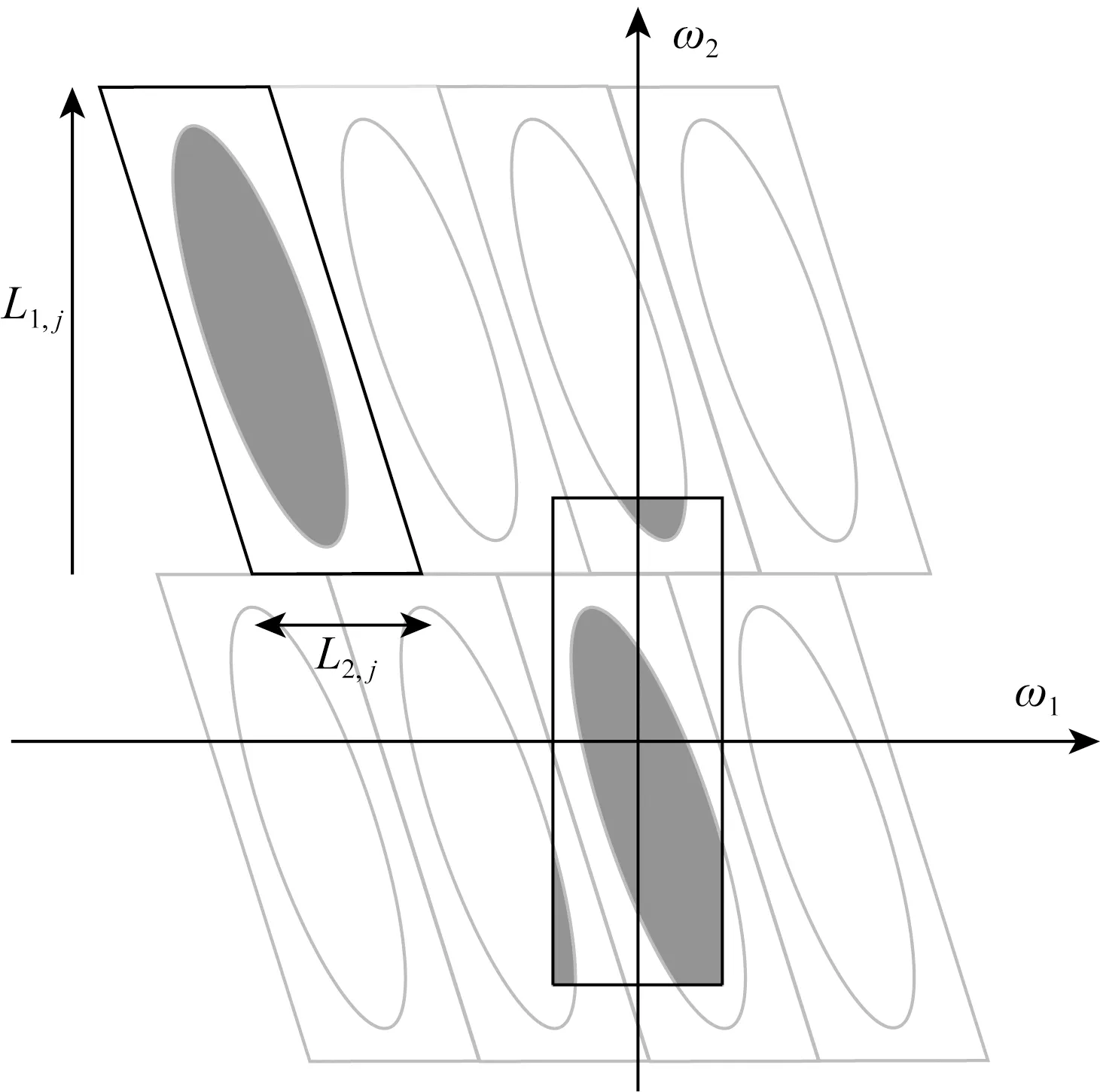
图4 曲波变换中的Wrapping算法(参考Candès et al.，2006)Fig.4 Wrapping algorithm in curvelet transform(Refer to Candès et al.，2006)

1.2 基于阈值法的电磁数据调平

本节我们首先解释曲波变换可用于航空电磁数据调平的原因，然后讨论具体调平方法.我们这里不考虑测区调平误差，而将注意力集中于测线调平误差和短波长调平误差.这是由于前者可采用较为简单的加/减背景场实现，而测线调平相对来说要困难的多.然而，曲波变换特别适合于对测线误差进行调平.事实上，如前所述，测线调平误差主要是由飞行方向改变导致的系统状态变化引起的，它们在垂直于测线的方向上具有相对稳定的空间尺度.另外，调平误差沿测线方向比较稳定(或者伴随缓慢的非线性漂移).所有这些导致该误差具有沿测线极强的方向性.因此，我们可以对信号进行多尺度和多方向分析，进而在曲波域特定尺度和角度方向上找出与调平误差相关的信息，进行有用信号和调平误差的有效分离，实现调平误差去除.

图5展示了理论模型的重构结果.图5a给出理论数据，我们分别将振幅为最大异常的12.5%及振幅为0的调平误差交替加入到图5a相邻测线的数据中，得到了图5b中包含调平误差的数据.考虑到理论模型共有60×60单元，我们在曲波域设置了4个尺度，分别在粗尺度上设置了小波系数，在第2尺度上设置了16个角度方向，在第3和第4尺度上设置了32个角度方向.进而，我们提取不同尺度和不同角度方向中的曲波系数，将信号重构回空间域，得到特定尺度和角度方向中的信号成分.从图5给出的结果可以看出，随着尺度参数j的增大，空间尺度逐渐变得精细.从图5f可以看出，调平误差集中在第4尺度，而从图5g—k可以看出，调平误差具有明显的方向性.对比图5h和图5k可以看出，第4与第20个角度具有相同的方向，这是由于它们在波数域中的支撑楔处于同一方向上的两个顶端.然而，由于这两个支撑楔存在位置、形态和对称性差异，它们包含的信息完全不同.最后，考虑到调平误差仅存在于第4尺度的第4、5、20、21角度方向，我们仅对这些尺度和方向进行数据调平，得到的结果由图5l给出.对比图5l和图5a可以看出，利用本文算法数据中的调平误差被去除，信号得到有效恢复.

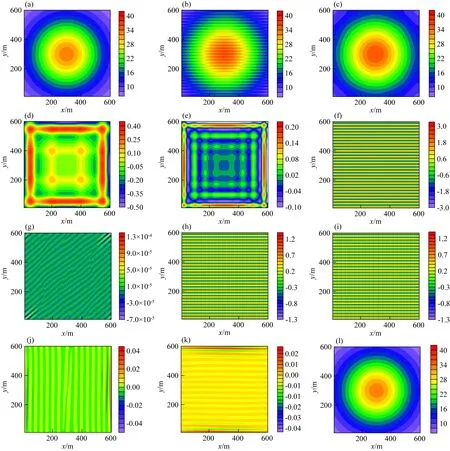
图5 理论模型及不同尺度、不同角度方向的重构结果(a) 原始数据； (b) 加入调平误差的数据； (c) 粗尺度重构结果； (d) 第2尺度重构结果； (e) 第3尺度重构结果； (f) 第4尺度重构结果； (g) 第4尺度第1角度重构结果； (h) 第4尺度第4角度重构结果； (i) 第4尺度第5角度重构结果； (j) 第4尺度第12角度重构结果； (k) 第4尺度第20角度重构结果； (l) 曲波变换调平结果.Fig.5 Theoretical model and reconstruction results from curvelet transform at different scales and angles(a) Original data；(b) Data with leveling errors added; (c) Coarse-scale reconstruction; (d) 2nd scale reconstruction result; (e) 3rd scale reconstruction; (f) 4th scale reconstruction; (g) Reconstruction of 1st angle from 4th scale; (h) Reconstruction of 4th angle from 4th scale; (i) Reconstruction of 5th angle from 4th scale; (j) Reconstruction of 12th angle from 4th scale; (k) Reconstruction of 20th angle from 4th scale; (l) Leveling by curvelet transform.

在确定了调平误差聚集的尺度和角度后，我们可以利用阈值法消除这些误差.本文中我们将硬阈值法、软阈值法两种方法应用于航空电磁数据调平.

硬阈值定义为

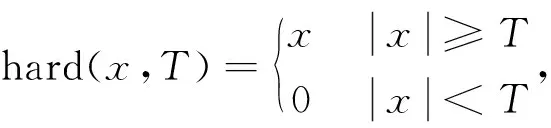
(18)

其中，x为曲波系数，T为阈值.硬阈值的主要思想是通过对低于阈值的系数进行置零来消除干扰.硬阈值法虽然易于实现，但其缺点是可能受局部畸变的干扰.为了使处理后的曲波系数更具连续性，我们定义如下形式的软阈值：

(19)

由(19)式可知，软阈值对所有系数都进行了修改.与硬阈值法相比，软阈值法可以得到更加平滑的结果，但可能给数据造成较大的失真.

本文将结合两种阈值方法的优点.为此，我们采取了2个步骤来消除调平误差：

(1)我们通过硬阈值法x=hard(x,Ta),x∈Xja,la消除典型的条带状误差；

(2)我们通过软阈值法x=soft(x,Tb)，x∈X去除上一步骤的残余误差及其他短波长误差.其中，集合X由所有的曲波系数组成，Ta、Tb是两个步骤中相应的阈值.

上述处理程序可以给出更进一步的说明.事实上，第一步中硬阈值法及相应阈值Ta主要用于调平误差集中的尺度和角度方向ja,la.由于调平误差的幅值未知，我们在这一步骤需要设置较大的阈值Ta，并采用硬阈值法以避免信号失真.当ja,la中调平误差幅值相对有用信号很大时，我们可以将所有ja,la内的曲波系数置零.然而，调平误差是非常复杂的，可能存在方向性不明显的局部扰动，或者存在第一步调平后的非线性残余.在这种情况下，我们可以对所有的尺度和角度应用软阈值法并设置阈值Tb，进一步去除前一步的调平残差和短波长误差.

在实际的数据处理中，首先通过曲波变换将数据转换至曲波域，然后根据调平误差的特征，选择合适的方向阈值或全局阈值进行处理.由于调平误差的复杂性，我们通过特定尺度和特定角度数据的重构判断所选阈值的合理性.若重构结果中方向性明显的误差消失，说明所选阈值合理可行.最后，我们将数据变换到空间域，如此便可以消除数据中的调平误差.

1.3 航空电磁数据调平步骤

航空电磁信号对飞行高度很敏感，因此在计算视电阻率或进行反演时，飞行高度往往作为变量.在对航空电磁数据进行调平时，我们需要首先校正飞行高度的影响.为此，我们采用Huang(2008)和Beiki等(2010)提出的方法，即利用收发距与飞行高度之比的立方对测量信号的实虚分量进行归一化处理：

(20)

(21)

其中，I和Q分别为电磁信号实虚分量，m和n为受飞行高度影响较小的归一化响应.Huang(2008)指出，当地下介质相对良导时，(20)和(21)式很准确；然而，对于高阻介质，为获得准确结果，式(21)中的(h/s)的阶数应该稍微降低.Beiki等(2010)利用这一近似将航空电磁信号校正到某一参考高度进行调平.本文中我们首先应用(20)和(21)式将数据进行归一化，进而利用上述基于曲波变换的调平方法对归一化的响应m和n进行调平，然后我们将数据转换回到实虚分量.最后,通过已调平的数据计算视电阻率.如果视电阻率中没有明显的条带状误差，则调平完成.由于曲波变换的多尺度和多方向特点，基于曲波变换的调平方法只对数据的某些细节尺度和角度进行局部改变，故对数据的原始相位关系影响很小，在去除调平误差时不容易引起数据畸变.

2 合成数据调平

下面我们首先测试本方法在合成数据调平上的有效性.考虑到调平误差可存在于各种航空数据中，本节仅给出不具有物理意义的合成模型.对于所有模型，我们在曲波域设置了5个尺度，角度数分别为第2尺度16个、第3、4尺度32个、第5尺度64个.图6a—c给出了原始数据、加入调平误差的数据以及调平误差，图6d给出了采用我们的曲波变换方法进行调平的结果，为对比起见，图6e给出了Huang(2008)提出的基于测线相关性调平方法的结果.对比图6d和图6e，我们发现基于测线相关性的调平方法更容易造成数据失真，这主要是由于该方法难以利用多项式拟合复杂的非线性调平误差.相比之下，曲波变换由于出色的二维信号表达能力，很好地还原了原始数据.从图6f和图6g展示的原始数据与调平后数据差中，我们也可以清楚地看到，本文方法的残差比其他方法的残差小.在点位(4000 m, 3000 m)附近，有一个延伸方向与测线相同的异常体.从理论上讲，这类异常体对于调平而言是较为困难的.然而，由于曲波变换的多尺度和多方向特性，我们成功地将调平误差从有效信号中分离出来，很好地恢复了该异常特征.

图6 (a) 原始数据； (b) 加入调平误差的数据； (c) 调平误差； (d) 曲波变换调平结果； (e) 基于测线相关性的调平结果(Huang，2008)； (f) 图(a)与(d)的差值； (g) 图(a)与(e)的差值Fig.6 (a) Original data； (b) Data with leveling errors； (c) Leveling errors； (d) Leveling of curvelet transform; (e) leveling of line-to-line correlation by Huang (2008)； (f) Difference between (a) and (d)； (g) Difference between (a) and (e)

航空电磁中经常会出现测线方向与大地坐标系不一致的情况.此时，传统的调平方法(例如基于二维滤波的方法)需要对坐标系进行旋转.由于曲线变换的方向性，我们可以省去这些旋转，仅通过选择不同的角度参数很容易地解决问题.这意味着基于曲波变换的调平方法具有更大的灵活性.图7给出一个测线与大地坐标轴斜交的模型和对应的曲波变换调平结果.由图可以看出，调平误差被很好地消除.

图7 (a) 原始数据； (b) 加入调平误差的数据； (c) 曲波变换调平结果Fig.7 (a) Original data； (b) Data with leveling errors； (c) Leveling of curvelet transform

航空电磁法中另一个常见的问题是测区形状不规则.在这种情况下，数据调平不仅费时，而且调平结果也会受到影响.例如，基于测线相关性的调平方法必须对拟合多项式进行外插，而基于二维滤波的调平方法在不规则的边缘处会产生一定的边缘效应.然而，基于曲波变换的调平方法由于具有多尺度性，可以有效地处理不规则测区获取的数据.事实上，在调平过程中，我们用一个常数来填充缺失的区域，然后进行调平.由于缺失区域具有一定的尺度，该区域的信息大多出现在曲波域的粗尺度上，对调平结果影响较小，因此在完成数据调平后我们仅需将该区域的数据剔除即可.图8给出形状不规则的合成模型的调平结果.由图可以看出，尽管测区由于存在三角形缺失变得不规则，调平误差仍然被很好地消除，数据得到有效地恢复.

图8 (a) 原始数据； (b) 加入调平误差的数据； (c) 曲波变换调平结果Fig.8 (a) Original data； (b) Data with leveling errors； (c) Leveling of curvelet transform

3 实测数据调平

为了进一步验证本文方法的有效性，我们将其应用于爱尔兰Waterford地区利用频率域航空系统采集的电磁数据.该项目由爱尔兰地质调查局(GSI)牵头，由加拿大Sander地球物理公司与Unicorn矿业有限公司合作组织实施.图9给出Waterford测区的位置及测线布设情况.其中，测线方向为N15°W，线距200 m，切割线方向为E15°N，线距2000 m.我们选择图9中红色线框标注的面积约为11.5 km×13 km的区域进行测试.我们在曲波域中设置5个尺度，其中第2尺度包含32个角度,第3、4尺度包含64个角度，第5尺度包含128个角度.我们以频率912 Hz为例对实测数据实虚部进行调平.

图9 Waterford项目测区位置及测线布设(修改自Bates和Cho, 2016)Fig.9 Survey area and survey lines for the Waterford project(Modified from Bates and Cho, 2016)

图10a和图10d为实、虚部原始数据.我们首先利用(20)、(21)式将数据转换为归一化响应m和n，然后利用本文方法对m和n进行调平，再将数据转换到调平后的实虚分量.图10b和图10e为调平后的数据.为了便于比较，我们在图10c和图10f中还展示了GSI采用的基于微分多项式拟合的调平结果(Beiki et al.，2010).由对比结果可见，对于虚部数据，基于曲波变换和基于GSI的多项式拟合方法均获得很好的结果；对于实部数据，基于曲波变换的调平方法有效去除了调平误差，未对数据产生明显的畸变，然而，GSI利用的多项式拟合方法在消除调平误差的同时，也去除了同方向上的异常(图10c).

图10 爱尔兰Waterford测区实部(左侧)与虚部(右侧)数据调平结果(a)与(d)为原始数据； (b)与(e)为曲波变换调平结果； (c)与(f)为GSI的调平结果.Fig.10 Leveling results of in-phase (left column) and quadrature component (right column) for the data from Waterford project, Ireland(a) and (d) Original data； (b) and (e) Leveling by curvelet transform； (c) and (f) Leveling by GSI.

由于本文方法对实虚分量的处理是独立进行的，因此对于调平结果来说，检验其视电阻率和相位变化至关重要.图11给出图10中调平前后数据计算的视电阻率和相位.由图可以看出，由于实虚部数据中含有调平误差，故利用原始数据计算视电阻率及相位时，误差被引入其中，导致计算结果中存在明显的条带状误差.经曲波变换调平后，视电阻率数据中的条带状误差明显减少，相邻测线间电性趋于相容、合理.作为对比，由GSI给出的调平结果计算得到的视电阻率在中间相对高阻区域仍存在明显的条带状误差，且造成了一定程度的数据畸变，特别是相位数据畸变更为严重.这主要是由于该方法在分别对实虚部进行调平时对原始数据畸变过多造成的.从图11d、e、i、j可以得出相似的结论，即本文的调平方法对原始数据的视电阻率和相位畸变较小.

图11 爱尔兰Waterford测区调平前后数据计算得到的视电阻率(左侧)与相位(右侧)(a)与(f)由原始数据得到； (b)与(g)由曲波变换调平结果得到； (c)与(h)由GSI提供的调平结果得到； (d)与(i)分别为(a)与(b)、(f)与(g)的差； (e)与(j)分别为(a)与(c)、(f)与(h)的差.Fig.11 Apparent resistivity (left column) and phase (right column) before and after leveling for the data from Waterford project, Ireland(a) and (f) From original data; (b) and (g) From results by curvelet transform； (c) and (h) From results of GSI; (d) and (i) Differences between (a) and (b), (f) and (g)；(e) and (j) Differences between (a) and (c), (f) and (h).

4 结论

本文我们基于曲波变换成功地开发了一种航空电磁数据调平方法.该方法较之于传统数据调平方法具有如下优势：

(1)利用曲波变换多尺度和多方向的优点，可以方便地提取与飞行方向相关的调平误差，同时有效保留了原始信号.

(2)对于实虚部数据的调平仅在曲波域的部分尺度和方向上进行，保留了实虚部数据中的主要成分，因此由其计算的视电阻率在调平误差被极大削弱的同时，原始相位关系得到很好保证.

(3)对于倾斜测线及不规则测区，本文调平方法无需坐标旋转和测区分割，同时避免了传统方法产生的边缘效应，具有很好的实用性.

理论和实测数据的实验结果均表明，本文基于曲波变换的调平方法比传统调平方法取得了更好的效果.由于调平误差在航空地球物理数据中广泛存在，而本文提出的方法实质上与数据类型无关，我们可以期待将该方法进一步推广应用于其他航空地球物理数据处理中.

致谢感谢爱尔兰地质调查局(GSI)与加拿大Sander地球物理有限公司允许本文使用他们的Waterford数据并提供技术支持.