基于极限学习机的复杂制造系统动态调度

马玉敏，陆晓玉，乔 非，沈一路

(同济大学 电子与信息工程学院，上海 201804)

0 引言

复杂制造系统生产过程复杂，由多个相关联的生产过程构成[1]。当制造过程比较平稳时，原定调度策略能够持续保证系统生产性能的优化；而当制造系统出现机器故障等扰动时，制造环境发生变化，先前采用的调度策略失效，最终无法得到期望的生产性能[2]。因此，如何根据生产过程状态动态地确定有效的调度策略是提高复杂制造系统运行性能的关键。这种根据制造系统生产状态来动态调整调度策略的方法即为复杂制造系统动态调度。

针对调度问题，国内外学者已经展开全面深入的研究，并取得了不少成果，其中包括启发式方法、仿真方法等[3-4]传统调度方法，也包括遗传算法、人工神经网络[5-6]等人工智能背景下的新调度方法。Wang等[7]为解决动态多目标调度问题，在精英非支配排序遗传算法中引入了有向搜索策略；Pickardt等[8]针对半导体制造中的动态作业车间问题，将遗传规划算法与进化算法相结合，提出一种两阶段的超启发式方法；Lou等[9]针对制造车间动态环境中的不确定性，提出一种基于多智能体主动式的调度方法和体系结构，并采用分布式调度算法求解动态调度问题。现有方法在解决调度问题上已展示出很好的有效性，然而随着制造系统复杂程度的增加(如设备、产品的数量大规模增加，多工艺约束限制等)，使得对制造系统的建模愈加困难，模型的不准确性会降低其给出的调度策略的可靠性，进而无法获得令人满意的调度结果。

数据驱动建模的方法精确度高且计算效率高[10],将数据驱动思想运用在生产调度领域，采用有效的方法分析累积的生产数据，提取相关知识并用于指导生产，是制造系统动态调度问题研究的重要方向[11]。

机器学习是数据驱动建模的有效方法，基于机器学习获得的数据驱动的动态调度模型，大致可分为两大模式：①分类模式，是指在动态调度过程中从已有的调度策略集中选择其中的一个调度策略来满足制造系统的调度目标;②回归模式，是指在动态调度过程中为含参数的调度策略给定一组特定的参数值，实现制造系统的调度目标。

应用机器学习分类算法从历史生产数据中获取分类调度模型，指导制造系统运作。Choi等[12]基于历史生产数据，利用决策树获得不同生产状态下的调度规则；Zhou等[13]针对半导体生产线光刻区的动态调度问题，采用K最近邻(K-Nearest Neighbors, KNN)算法进行数据挖掘，以指导实时调度过程中调度规则的选取；吴启迪等[14]研究了一种数据驱动下的半导体生产线调度框架，基于调度优化数据样本，通过机器学习获得动态调度模型，指导半导体生产线动态调度。分类模式将简单的调度规则与数据驱动思想相结合解决动态调度问题，在提高求解效率的同时也改善了求解精度，但由于简单调度规则的局限性，使得其难以满足制造系统多目标调度的需求。应用机器学习回归算法建立回归调度模型，可以使模型根据制造系统的实时生产状态得到相匹配的调度参数指导制造系统生产。Heger等[15]提出一种根据当前系统条件动态调整调度规则参数的方法，采用高斯过程回归评估不同参数对生产性能的影响；Li等[16]应用二元回归模型、BP神经网络和粒子群算法得到自适应调度规则参数与实时状态的关系。回归模式将含参数的复合调度规则与数据驱动思想相结合解决动态调度问题，与具体的制造系统相耦合，易于解决制造系统多约束的需求。

复杂制造系统的动态调度是一个多约束、多目标优化问题，本文拟采用数据驱动方法来解决复杂制造系统动态调度问题。常见的数据驱动调度方法多基于分类调度模型，通常以简单的启发式调度规则为调度策略，难以满足制造系统多目标多约束的要求。因此，本文以线性组合式调度规则[17]为调度策略，应用极限学习机(Extreme Learning Machine, ELM)得到回归调度模型，使其能实时生成与生产状态相适应的调度规则权重组合，即组合式调度规则，达到制造系统的多目标优化。

1 复杂制造系统动态调度框架

数据驱动的复杂制造系统动态调度通常可分为调度模型的离线学习阶段和调度模型的在线应用阶段两个阶段。调度模型的离线学习，即在离线状态下根据调度目标采用机器学习方法分析历史数据，建立调度模型，实现生产状态和调度策略之间的映射；调度模型的在线应用，即在线动态调度时应用调度模型给出与实时状态相匹配的调度策略。复杂制造系统动态调度框架如图1所示，它由数据采集、数据处理、机器学习和在线动态调度4部分组成。

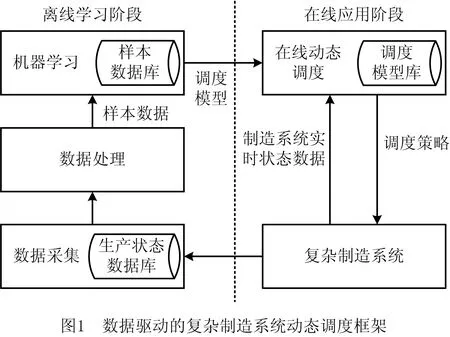
(1)数据采集 从制造系统/仿真模型获取生产状态数据，包括制造系统状态、调度策略和性能指标。

(2)数据处理 基于获取的生产数据，采用试验设计等方法生成调度策略最优样本集。

(3)机器学习 在最优样本集的基础上，根据不同的调度目标采用机器学习建立相应的调度模型，并存放于调度模型库中。

(4)在线动态调度 在线调度时，根据调度目标，调用相应的调度模型，以制造系统实时生产状态数据为输入，输出满足调度目标的调度策略。

2 数据处理

2.1 调度策略

启发式调度规则根据工件的属性信息，如加工时间、交货期等，计算待加工工件的优先级，得到加工次序。该规则简单且易于理解和执行，是制造系统动态调度中最常用的调度方法。每个启发式规则都能满足特定的调度目标。例如，为了提高订单按时交货率，可选用最早交货期优先(Earliest Due Date, EDD)调度规则。在复杂制造系统中，多目标、多约束是生产调度的难点，单一的调度难以满足该需求，为此许多专家学者提出用组合调度规则来进行生产调度[18-19]。本文以课题组设计的一种组合式调度规则作为调度策略[17]，将多个不同调度目标的调度规则有机结合在一起，其定义工件排序所用的综合优先级Pi如式(1)所示：

(1)

s.t.

其中：pj,i为调度规则j确定的工件优先级；wj为规则j的权重系数，表示该调度规则在组合式调度规则中的重要程度，在很大程度上影响了工件的加工优先级，从而影响调度结果。因此，需要根据调度目标对组合式调度规则的权重系数进行合理分配。

2.2 基于试验设计的优化调度样本的获取

当采用组合式调度规则对制造系统进行调度时，需要对其权重系数进行合理分配，以达到期望的调度目标。试验设计方法(Design of Experiments, DOE)是通过主动控制影响因素的变化，进而观察响应变量的变化，并研究其中影响的一种方法[20]。本文采用试验设计，以组合式调度规则权重系数为试验变量、制造系统的生产性能为响应变量进行试验，建立生产性能的响应函数，根据调度目标优化组合式调度规则权重系数。

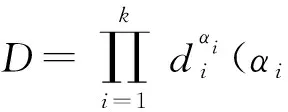
为提高生产性能响应函数的精度，将权重系数优化过程分为两个阶段：第一阶段采用单形格子设计法，获取较优的权重系数取值范围；第二阶段采用D-优化设计法，在较优的权重系数取值范围内确定最优的权重系数取值。

(1)第一阶段：确定权重系数的取值范围

(2)第二阶段：确定最优权重

在第一阶段得到的权重较优范围内进行D-优化设计[23]，以拟合一个更加精确的高阶模型。即基于单形格子设计确定的组合式规则权重取值范围，其最优值的选取可以看作是一个带有约束条件的混料试验。根据D-优化设计确定的试验点，运行复杂制造系统仿真模型，得到试验数据，可建立响应值与参数变量间的函数关系，再利用满意度函数法进行优化，即可得到一组该生产状态下组合式调度规则的最优权值系数。

3 基于FCM-ELM的调度模型的学习

3.1 基于ELM的调度模型

通过数据处理阶段对生产数据的优化处理，可以得到组合式调度规则权重系数最优的样本集：A={Xi,Yi,Pi|Xi∈Rm,Yi∈Rn,Pi∈Rk,i=1,2,…,N}，即对于生产状态Xi在最优组合式调度规则系数Yi的条件下，生产性能Pi最优。ELM是一种新兴的数据挖掘算法[24]，通过样本学习将输入、输出参数形成一个网络映射结构，构成回归模型。由于其具有简单快速等特性，应用广泛。本文采用ELM建立组合式调度规则中权重系数的回归模型，样本为{Xi,Yi|Xi∈Rm,Yi∈Rn,i=1,2,…,N}，其中：Xi=[xi1,xi2,…,xim]T为模型的输入，表征制造系统生产状态，xim为第m个生产状态特征；Yi=[yi1,yi2,…,yin]T为模型的输出，表征当前生产状态Xi所对应的最优调度策略，即组合式调度规则的权重系数，yin为第n个规则的权重。通过样本学习，构成复杂制造系统生产状态与组合规则权重系数的网络映射关系，如图3所示。

所得到的ELM调度模型可表示为：

i=1,2,…,N。

(2)

式中：L为隐层节点数;G(x)为激励函数;Wj=[wj1,wj2,…,wjm]T为第j个隐层节点与输入节点的权重向量;βj=[βj1,βj2,…,βjn]T为第j个隐层节点与输出节点的权重向量;bj为第j个隐层节点的偏置。

在学习调度模型过程中，隐层节点数L的选择对调度模型的精度有一定影响，本文将采用枚举法进行寻优，找出合适的隐层节点数L，以保证所建调度模型的精度。

3.2 基于FCM-ELM的调度模型

复杂制造系统的生产状态随着制造系统的产品种类、工艺参数，设备状态和负荷不同而变化，一个调度模型很难精确地反映出制造系统不同状态(如轻载、满载和重载)下的调度知识。为保证通过数据学习到的调度知识的准确性，首先采用聚类方法将相似的样本聚类，再对每一类分别训练调度模型，形成一个综合的调度模型库，供调度使用。模糊聚类方法是常用的聚类方法[25]，包括布尔矩阵法、基于摄动的模糊聚类分析法、模糊C均值聚类(Fuzzy C-Means, FCM)等。其中，基于目标函数聚类的FCM算法简单易用且分类效果好，本文将采用FCM算法对最优样本进行聚类处理。

FCM算法基于划分的思想，使得被划分到同一类的对象之间相似度最大，而不同类之间的相似度最小。基于FCM算法对样本{Xi,Yi|Xi∈Rm,Yi∈Rn,i=1,2,…,N}进行聚类，其目标为所有样本距离聚类中心的距离指标价值函数最小，即

(3)

s.t.

(4)

μij∈[0，1]，i=1,2,…,C，j=1,2,…,N;

(5)

dij=‖xj-ci‖,i=1,2,…,C，j=1,2,…,N。

(6)

其中：C为聚类个数，ci(i=1,2,…,C)为每个聚类的中心；μij∈[0,1]为第j个样本对第i类的隶属度(1表示完全隶属于，0则表示完全不属于)；dij是样本xj和聚类中心ci的欧氏距离，b为平滑因子。求解式(3)即可找到隶属度最高的聚类中心，将生产调度数据样本按照状态值合理分为多类。

由此，在最优样本的基础上，采用FCM聚类算法和ELM回归算法学习复杂制造系统调度模型的具体步骤为：

步骤1样本生成，即经上述组合式规则权重参数优化过程，得到不同生产状态下最优的调度策略，形成用于调度模型学习的样本数据集。

步骤2将最优样本全集A以生产状态X为聚类特征变量，即将生产状态作为FCM算法的输入，将样本全集A根据相似的生产状态分为k个子集A1,A2,…,Ak。

步骤3调度模型的学习。对每一生产子集，建立基于ELM的调度模型，输入为制造系统生产状态，输出为组合式调度规则的权重系数，其中，ELM的隐层节点数L采用枚举法选择获得。

步骤4对建立的ELM调度模型进行测试，并分析结果。采用根均方误差(RMSE)衡量调度模型的精度，评价所建立的模型效果，定义为：

(4)

ELM调度模型学习得到后，即可供在线调度使用。在动态调度点，可实时获得与当前生产状态相匹配的调度策略，指导实际生产。

4 实验验证

4.1 实验对象和基础数据

MIMAC模型是由美国亚利桑那州立大学工业工程系半导体制造实验室提供的一组半导体生产线模型。该套数据全部取自真实的半导体晶圆厂，由若干半导体制造领域知名企业和学者联合发布。其中MIMAC6模型包含104个设备群、228台设备。模型中有9种产品，每种产品都有上百道工序，是典型的复杂制造系统模型。本文以MIMAC6模型为实验对象来验证本文所提出的数据驱动的复杂制造系统动态调度方法的有效性。实验在Intel Core i3 CPU、内存为4 G、操作系统为Windows 7的计算机上进行，样本优化采用软件Design Expert 10实现，算法使用MATLAB编程实现。

(1)生产状态特征集

这是一组表征制造系统生产状态特征的数据，描述了复杂制造系统中工件和各加工区生产设备的状态，如表1所示。

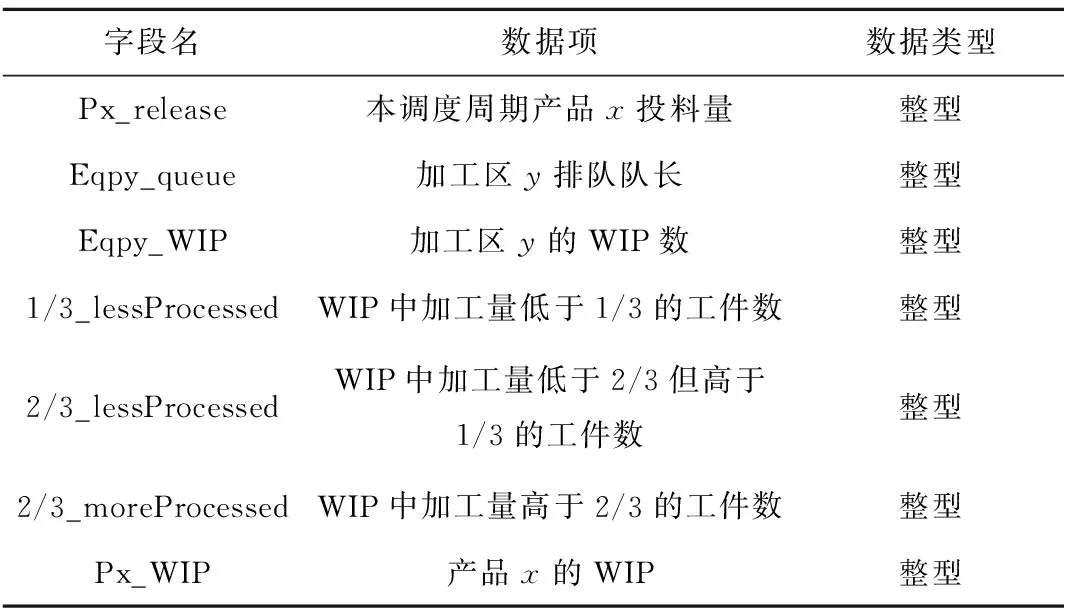
表1 生产状态集

(2)性能指标集

选取制造系统中工件的平均加工周期MCT、工件的日平均移动步数MDayMOV、制造系统生产率PROD、所有设备的平均利用率OEE四个性能指标作为调度优化目标，其中MCT和PROD为长期性能指标，MDayMOV和OEE为短期性能指标。实验中，综合考虑长、短期性能指标，以更好地优化制造系统生产运行。

(3)调度策略

结合待优化的生产目标，选取先进先出(First In First Out, FIFO)、最短加工时间优先(Smallest Processing Time, SPT)、临界值优先(Critical Ratio, CR)三种调度规则进行组合，按照式(1)形成组合式调度规则。

4.2 基于FCM-ELM的调度模型的动态调度结果

运行MIMAC6仿真模型获取生产状态数据，经试验设计获取含样本数为300条的最优样本集，同时使用FCM算法对样本进行聚类，并采用ELM算法建立调度模型，形成调度模型库，供动态调度使用。

(1)ELM调度模型学习参数选择

采用ELM算法学习调度模型时，其中的学习参数，即隐层节点数L的选择对所建立模型的精度有一定影响。在[0,30]的取值范围内，对隐层节点数L进行讨论，采用枚举法对L的取值进行遍历，利用根均方误差以及模型训练时间对所建调度模型进行评价，从而获得最优的隐层节点数L取值。

根均方误差RMSE越小，则所建立的调度模型越精确。在实验中得到L的取值范围在[20,30]时，模型的精确度较高。由图4可知，当L=24时RMSE值最小，且此时的模型训练时间也未受影响，保持在平均水平以下。因此，在实验中，学习调度模型时，ELM的隐层节点数L=24。

(2)动态调度结果分析

为分析动态调度方法的效用，本文对复杂制造系统在订单数据动态变化时，不同调度方法对其性能的影响进行了分析。订单数据动态变化体现在日投料(产品混合比)上，将MIMAC6预热15天，设置9种产品的日投料数服从[1,4]均匀分布，运行30天后进行采样，随机采集20种不同的生产状态用作测试，其日投料和在制品数据各不相同。在20种生产状态下，运行MIMAC6仿真模型，分别执行根据模糊C均值聚类—极限学习机(FCM-ELM)和极限学习机(ELM)调度模型生成的调度策略，以及先进先出FIFO、最短加工时间优先SPT、临界值优先CR三种启发式规则，记录制造系统生产性能，分析并比较它们在不同调度策略下的生产性能，如图5～图8所示。

分析图5～图8中20种不同生产状态在不同调度方案下的4种性能指标MCT、PROD、MDayMOV和OEE，分别与单一规则进行对比，采用基于FCM-ELM以及ELM的动态调度方法表现出总体的有效性。计算不同调度策略下20组样本各性能指标的平均值，不难发现，基于FCM-ELM的动态

调度方法，在PROD上表现最好，较FIFO、SPT、CR平均高出41.25%(约多1.87 lot/天)、31.75%(约多1.54 lot/天)、1.16%；在OEE上较FIFO、SPT、CR平均高出0.96%、2.02%、1.48%；在MDayMOV上较SPT、CR平均高出3.34%、2.11%，但较FIFO平均降低0.5%；在MCT上较FIFO、SPT平均降低16.60%、7.24%，但较CR平均高出0.82%。

为了更好地比较不同调度策略的综合效果，按照性能优劣进行归一化处理，将各指标平均值转化为[0,1]范围内，取值为0即性能最差，取值为1即性能最优。绘制各调度策略的性能指标雷达图(如图9)，雷达图所占面积越大，说明其综合性能越好。

由图9可知，在5种调度策略中，基于FCM-ELM的动态调度方法和基于ELM的动态调度方法的性能雷达图面积比其他3种单一规则的性能雷达图面积大。这是因为当动态调度应用单一规则时，调度规则不会随系统状态的变化而变化，即没有考虑采用的调度规则与当前制造系统状态是否匹配，因此产生的综合生产性能劣于基于FCM-ELM和基于ELM的动态调度方法；而基于FCM-ELM的动态调度方法的4种性能指标的归一化值均在[0.6,1]之间，雷达图的面积最大，即综合性能优于基于ELM的动态调度方法，说明先聚类再学习得到的调度模型更有效。

5 结束语

本文针对复杂制造系统调度多约束多目标的特点，提出了数据驱动的动态调度方法。基于组合式调度规则，通过试验设计方法生成调度策略最优样本集，设计了基于FCM-ELM的动态调度方法，即先对优化样本进行聚类再进行调度模型的学习，以满足复杂制造系统调度的多态性和实时性。最后，在MIMAC6模型上验证了所提方法在综合性能上较单一调度规则及不经聚类的ELM动态调度方法均有显著提升。所提动态调度方法能够有效地解决多变场景下的制造系统动态调度问题，适用于生产需求波动频繁、产品品种多以及工艺复杂的制造车间，如半导体制造业、汽车制造业等。

但是在数据驱动的复杂制造系统动态调度中，时间代价最大的是数据处理部分。后续工作中，如何快速有效地获取足够的学习样本是数据驱动的动态调度需要解决的一个难点。