基于精确弓高误差校核的刀触点调整算法*

闵 莉 宋航远 王 野

(沈阳建筑大学机械工程学院，辽宁 沈阳110168)

近年来，我国装备制造业飞速发展，高精加工技术领域市场需求也愈发高涨，数控技术进入了前所未有的高速发展阶段。随着加工技术的广泛应用，许多复杂自由曲面加工难题得以解决，因此，五轴数控加工技术对于数字化加工制造技术有着十分重要的意义[1]。

自由曲面刀具轨迹规划是对复杂曲面进行数控加工的关键环节。刀具轨迹规划算法对加工效率和表面质量有着直接的影响。其中，走刀步长的研究又是刀具轨迹规划中至关重要的一环。现有关于步长的研究有：基于机床运动学模型计算走刀步长的方法[2]；基于刀具、刀路几何信息及机床结构参数等因素，通过优化机床逼近拟合曲线的误差优化走刀步长方法[3]；基于补偿机床自身非线性误差从而优化走刀步长方法[4]；基于切削力模型的刀触点确定算法[5]；基于Dijkstra算法的走刀步长计算方法[6]；实时NURBS曲线插补算法研究[7-10]；弓高误差中点校核算法研究[11-12]。但在实际加工中，最常用的还是传统的走刀步长计算方法：等参数步长法、等距步长法以及等弓高误差步长法[13]。其中等弓高误差步长法采用近似替代的方法，假设相邻两刀触点之间为等半径圆弧计算步长，将会产生一定的误差。因此本文基于等弓高误差法的不足，加入了精确弓高误差的校核计算，重新搜索调整实际刀触点的精确位置。

1 等弓高误差步长法

1.1 等弓高误差法的计算

已知曲面为S(u,v)，假设刀具路径曲线为P(t)，则有：

P(t)=P(u(t),v(t))

(1)

假设同一条路径曲线P(t)上相邻两刀触点间的曲线为等半径圆弧，即Ri=Ri+1。若已知许用弓高误差[ε]、当前刀触点P(ti)以及该点在路径曲线P(t)上的曲率半径Ri，即可计算出步长Li，继而求出后一刀触点P(ti+1)位置。

如图1所示，通过勾股定理可得：

(2)

由式(1)可得步长Li：

(3)

由二阶泰勒展开可得参数增量Δt：

(4)

故后一刀触点P(ti+1)位置：

ti+1=ti+Δt

(5)

P(ti+1)=P(ti+Δt)

(6)

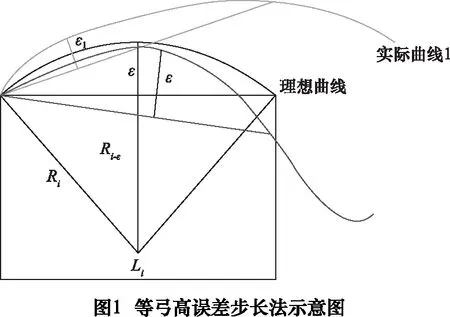
1.2 等弓高误差法的不足

由1.1节可得到后一刀触点P(ti+1)。但是，在计算过程中，采用了大量的近似代替。首先，在整个计算过程中，将P(ti)与P(ti+1)两刀触点之间的圆弧用等半径圆弧代替，假设Ri=Ri+1；其次，在计算参数增量Δt的过程中采用了泰勒二阶展开，并省略了余项；最后，从几何上来讲，任意一条曲线都可能存在若干二阶导数为零的点，即拐点。而如果当前刀触点P(ti)恰好落在当前路径曲线的拐点附近时，该点的曲率半径将接近无穷大，从而导致由上述公式计算得到的步长Li可能会离奇增大，从而导致实际弓高误差远大于许用误差。

2 精确弓高误差步长算法

基于1.2节所述的不足，本文在其基础上加入了精确弓高误差校核计算。通过比较P(ti)、P(ti+1)两刀触点之间的实际弓高误差εi(ti,ti+1)与许用弓高误差[ε]，进而调整后一刀触点P(ti+1)的实际位置。

2.1 精确弓高误差求解

首先通过1.1节传统的等弓高误差步长法，计算一个初始步长Li，继而求出初始参数增量Δti，得到后一刀触点P(ti+1)的初始位置。因为在加工中为保证拟合曲线的精确性，路径曲线在一个走刀步长内一定是单峰区间，故弧P(ti)P(ti+1)与弦P(ti)P(ti+1)的最大弓高误差只存在于一点处，我们只需要求出该参数点位置，即可求出精确的弓高误差。

由图2可知，当曲线P(t)中弧P(ti)P(ti+1)内某点P(tim)的切线斜率等于弦P(ti)P(ti+1)的斜率，则该点即为该步长内最大弓高误差点。

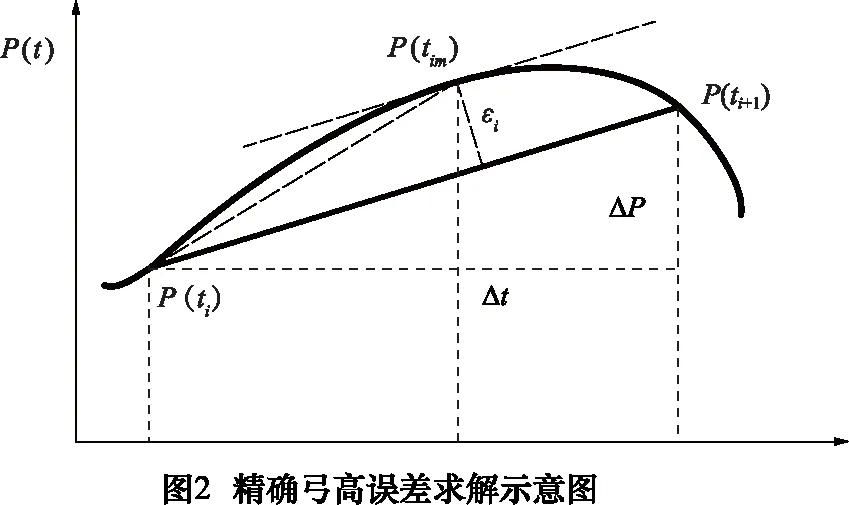
设弦P(ti)P(ti+1)的斜率为k1：

k1=ΔP/Δt

(7)

式中：Δt可由式(4)计算，ΔP即为两刀触点纵坐标差值。

设弧P(ti)P(ti+1)的斜率为k2：

k2=P′(t)

(8)

其中P′(t)为曲线P(t)对参数t求导：

(9)

最后，令两个斜率相等：

k1=k2

(10)

即可求出参数t=tim以及最大弓高误差点P(tim)。

该步长区间内的实际弓高误差εi的计算即可转化为点P(tim)到弦P(ti)P(ti+1)的距离。由距离公式可得：

(11)

2.2 参数最小可行区间T(tmin,tmax)求解

根据2.1节，校核实际弓高误差与许用弓高误差的大小。如果εi(ti,ti+1)>[ε]，向左调整后一刀触点P(ti+1)参数ti+1；如果εi(ti,ti+1)<[ε]，向右调整后一刀触点P(ti+1)的参数ti+1。最终输出ti+1的最小可行区间T(tmin,tmax)。

设ε(tm,tn)表示点P(tm)与点P(tn)点之间的实际弓高误差。算法流程图见图3。

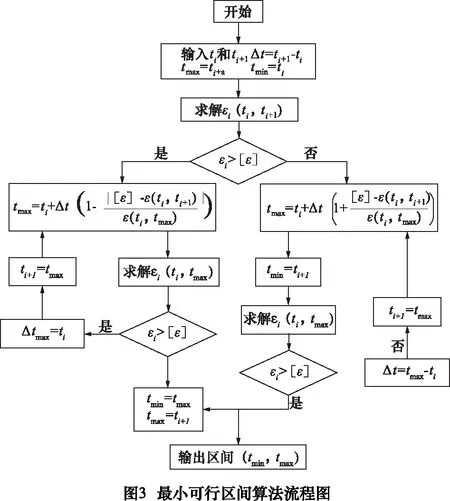
具体算法步骤如下：

(1)已知当前刀触点为P(ti)，通过传统等参数步长法计算出初始步长Li、初始参数增量Δti以及后一刀触点P(ti+1)的初始ti+1值。

(2)通过精确弓高误差公式(11)计算初始步长Li内的实际弓高误差εi(ti,ti+1)。

(3)判断εi是否大于[ε]。如果不是，跳转第(4)步；如果是，跳转第(6)步。

(4)令

随着机器视觉技术、3 G技术、电子技术的不断发展以及人们对农产品可视化生产程度和农产品质量安全水平要求的不断提高，农产品生产过程全程可视化监控已经逐渐成为精准农业的一个热门发展方向[1]。农产品生产过程中传统物理量参数的监控已经无法满足现代农业的发展趋势。

(12)

tmin=ti+1，向右搜索P(ti+1)，并重新计算εi(ti,tmax)，继续判断εi是否大于[ε]。如果不是，跳转第(5)步；如果是跳转第(9)步。

(5)令Δt=tmax-ti，ti+1=tmax，并跳转第(4)步。

(6)令

(13)

向左搜索P(ti+1)，并重新计算εi(ti,tmax)，继续判断εi是否大于[ε]。如果不是，跳转第(7)步；如果是跳转第(8)步。

(7)令Δt=tmax-ti，ti+1=tmax，并跳转第(6)步。

(8)令tmin=tmax，tmax=ti+1，并跳转第(9)步。

(9)输出区间T(tmin,tmax)。

采用这种迭代算法的优势在于：式(12)与式(13)内包含分式运算，通过比较差值[ε]-ε(ti,ti+1)与最大区间的精确弓高误差ε(ti,tmax)的大小，按比例的调整参数增量Δt，可以有效预测后一刀触点P(ti+1)的大概位置，有效减少迭代次数。

2.3 采用二分法求解P(ti+1)的实际位置

由2.2节可知，P(ti+1)必定位于区间T(tmin,tmax)之内，故本节将采用二分法逼近求解精确的参数ti+1，设e为迭代误差阈值。算法流程图见图4。

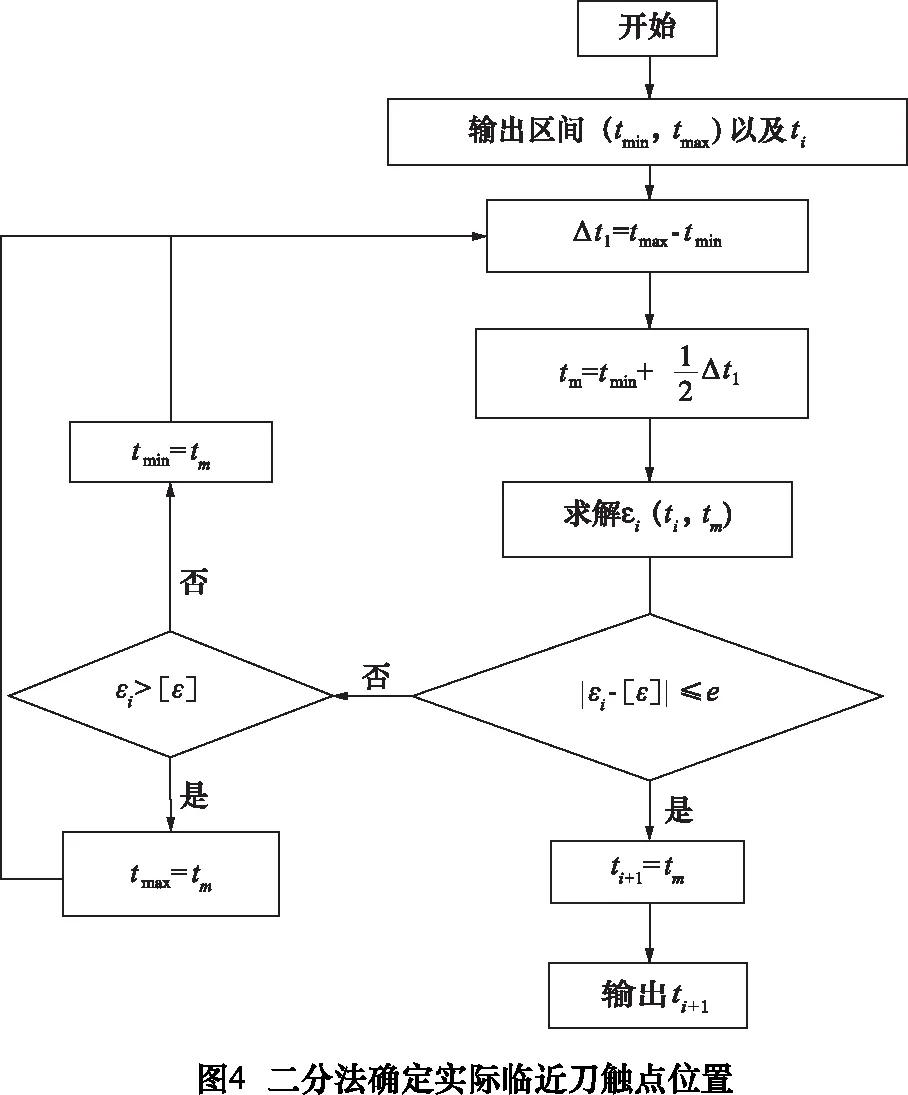
综上，通过2.2与2.3两节即可由当前刀触点P(ti)求出后一刀触点P(ti+1)的精确位置，最后将上述算法遍历整条路径轨迹曲线P(t)即可。

3 仿真实验

为方便展示分析，取其中一个实验结果为例。选取曲面上的一条刀具轨迹P(t)，设定许用弓高误差为[ε]=0.02，分别采用等参数步长法、等弓高误差步长法与本文算法对曲线P(t)进行离散。设置等参数法的参数增量为Δt=0.01，设置本文精确弓高误差步长法的迭代误差阈值为e=0.003。其结果如图5～8以及表1所示。

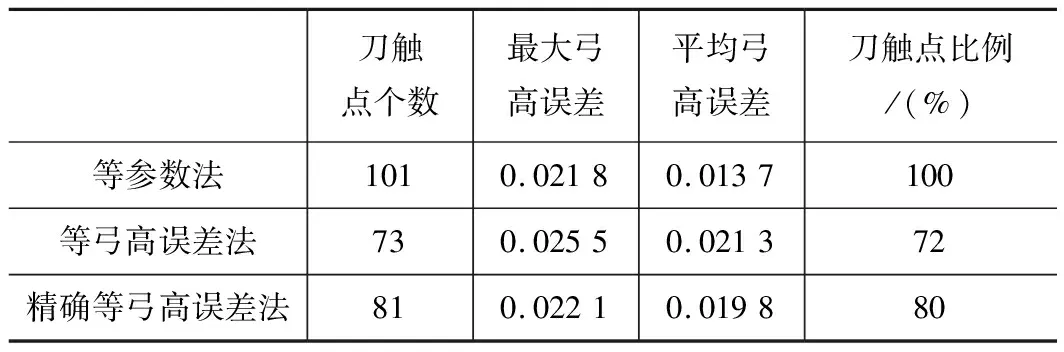
表1 三种方法误差对比表

由仿真结果可以分析出：

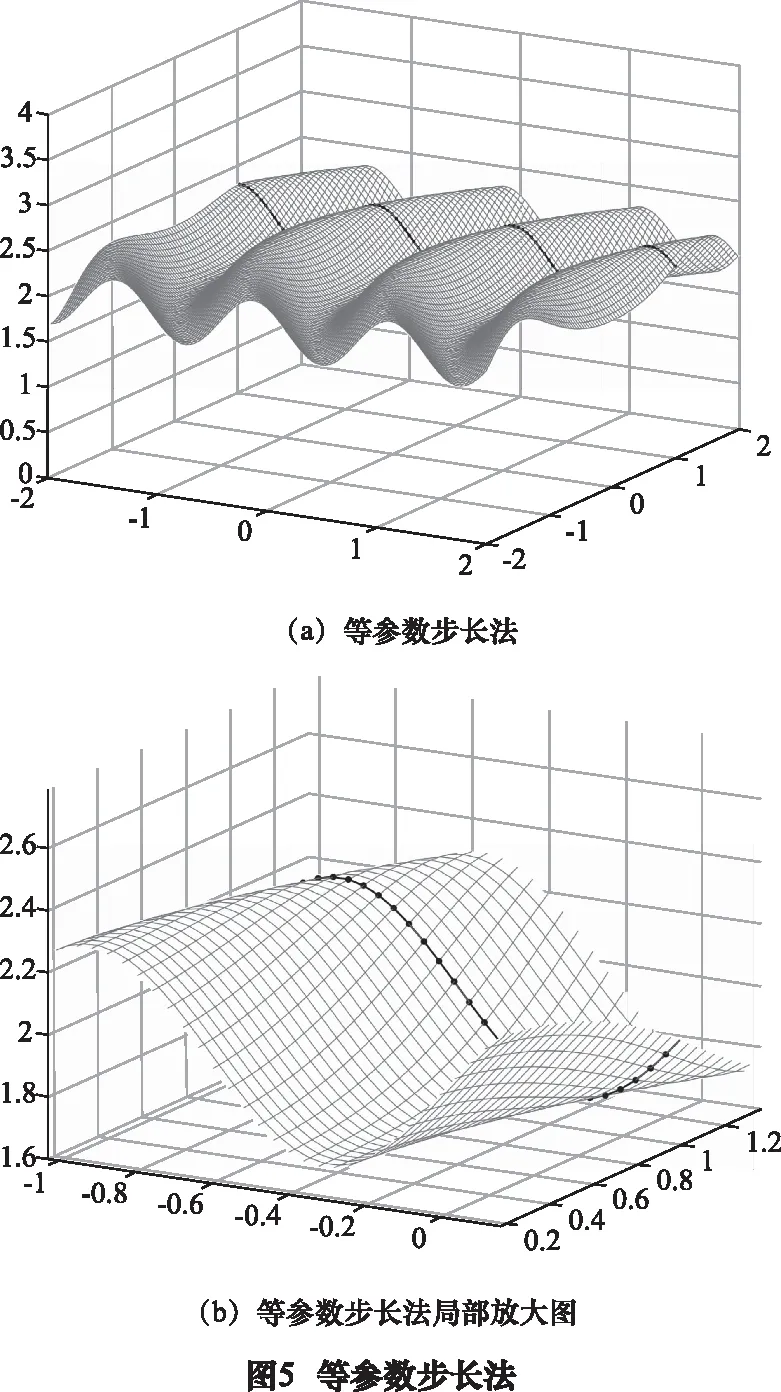
(1)采用等参数步长法离散曲线：曲线离散点在曲线上分布均匀，一共生成了101个刀触点(见图5)。但实际弓高误差变化较大(见图8)。在曲线曲率越大的区域，弓高误差越大，当曲率越小的区域，弓高误差越小，但总体误差远小于精度要求。

产生这种结果的原因就是该方法为了保证最大弓高误差满足要求，其参数增量往往取得过于保守，因此整体加工精度相对较高，但是导致相较其他两种方法产生最多的刀触点个数，加工效率最低。

(2)采用等弓高误差法离散曲线：曲线离散点在曲线上分布并不均匀，一共生成了73个刀触点(见图6)。弓高误差变化剧烈程度略小于等参数步长法，但总体弓高误差偏大。

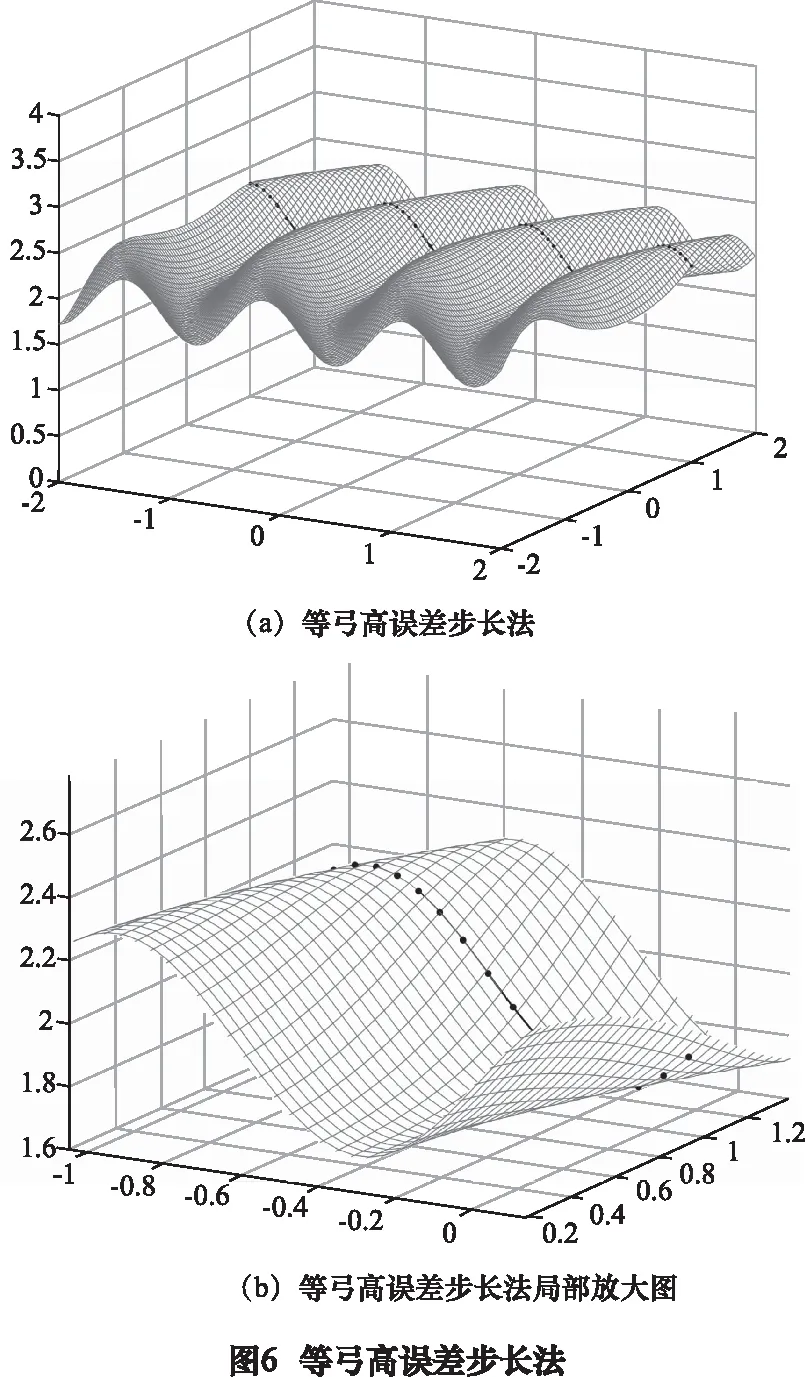
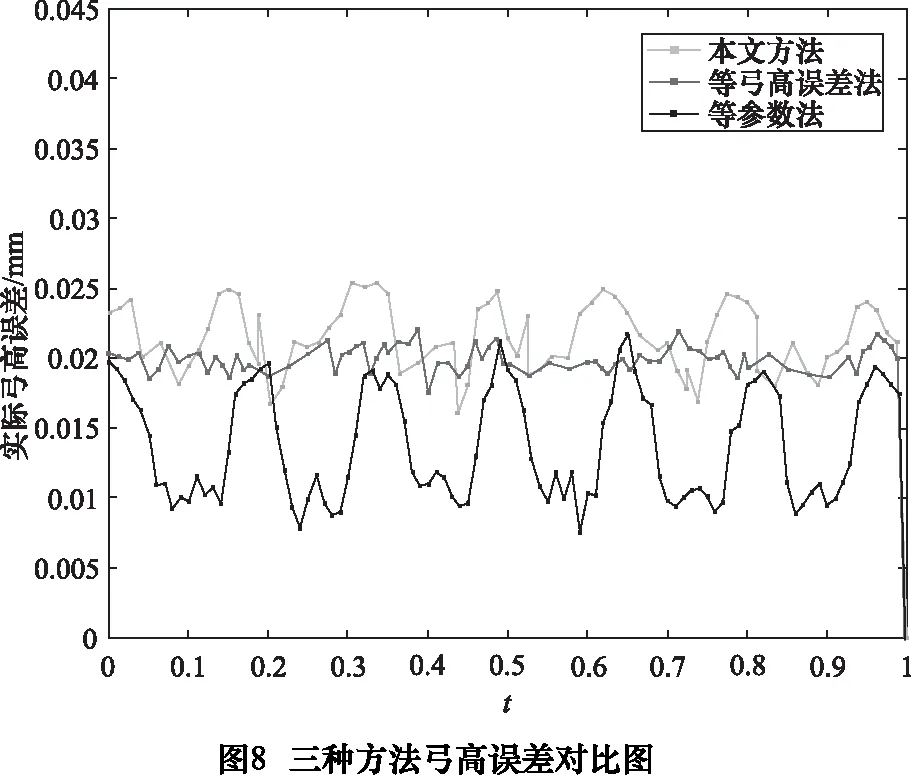
产生这种情况的原因就是等弓高误差步长法本身采用近似替代计算存在不足，导致实际弓高误差在许用弓高误差附近震荡，但普遍大于许用弓高误差。相较于其他两种方法，精度最低，但有着最少的刀触点个数，加工效率最高。

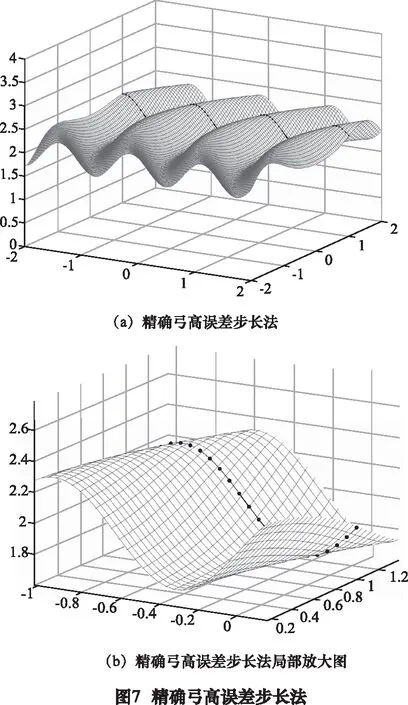
(3)采用本文的精确弓高误差步长算法离散曲线：曲线离散点在曲线上分布也不均匀，但本文方法会自适应曲线形状，在曲率较大的区域生成较多的刀触点，在较为平坦的区域生成较少的刀触点，一共产生了81个刀触点(见图7)。而且整体实际弓高误差变化十分微小，基本保持在许用弓高误差附近(见图8)。

结果表明，在许用弓高误差[ε]相同的情况下，本文算法相较于等参数步长法减少了20%的刀触点个数，有较好的加工效率(见表1)；相较于等弓高误差步长法又有更小的实际弓高误差值，有着更高的加工精度(见表1)。

产生这种情况的原因就是本文算法建立于等弓高误差步长法的基础之上，加入了实际弓高误差校核，搜索调整每个刀触点的位置，并且加入算法迭代精度，保证了实际弓高误差在许用弓高误差附近轻微幅度震荡。

4 结语

本文针对传统等弓高误差法的不足，提出了一种精确弓高误差校核计算的方法，并提出了一种一维线性搜索方法，在此基础上实现了对后一刀触点P(ti+1)点精确位置的调整。

针对相同曲面上的同一条刀具轨迹，本文的精确弓高误差步长算法相较于等参数步长法与等弓高误差步长法有如下优势：

(1)相较于等参数步长法能够自适应的生成刀触点，在相同许用弓高误差[ε]的条件下，有着更好的加工效率。

(2)相较于等弓高误差步长法在保留自适应生成刀触点的同时，能够更好地控制实际弓高误差数值，有着更高的加工精度。