Excel 在Top–Down 法不确定度评定中的应用

李镇冰，肖瑞娜，王启林，韩晓萍

(青海省药品检验检测院，青海省中藏药现代化研究重点实验室，西宁 810016)

Excel 丰富的函数和强大的数据处理功能使其在不确定度评定中具有广泛的应用，较为常见的是用于GUM 法和蒙特卡洛(MC)法不确定度评定［1–2］。GUM 法［3–5］是 一 种 基 于 测 量 模 型 的bottom–up （自下而上）方法，该法注重细节，需要分别评估测量模型的每一输入量及其影响因素，因此不同检测方法或项目的评定过程不完全相同，建立的Excel 电子表格不具有通用性。MC 法［6–7］基于测量模型，需要借助计算机程序来进行模拟，对计算机性能有较高要求，尽管可以通过Excel 实现，但是体验不佳。

Top–Down(自上而下)方法利用方法确认、内部质控、实验室间比对和能力验证等数据，能够全面反映检测全过程中各种因素的影响，更适合于化学检测领域。目前采用Top–Down 法评定不确定度的报道相对较少，而借助Excel 进行Top–Down 法不确定度评定则至今未见报道。这可能是由于相关的标准规范和指导原则专业性较强［8–12］，需要一定的统计学基础，因而Top–Down 技术没有得到广泛普及。

RB／T 141–2018 《化学检测领域测量不确定度评定 利用质量控制和方法确认数据评定不确定度》［13］，给出了使用Top–Down 法评定不确定度的简便方法，Top–Down 法只需考虑期间精密度和偏倚两个不确定度分量，且期间精密度和偏倚不确定度分量的各种评定方式非常简单明了，但涉及的数据量并不适合手工计算。Excel 非常适合用于此类逻辑不太复杂、数据量适中的统计分析工作。笔者依照RB／T 141–2018 中的不确定度评定方法，建立了包含测量系统正态性、独立性和一致性检验、期间精密度不确定度分量评定、偏倚不确定度分量评定，以及不确定度合成等功能的Excel 电子表格。

1 测量系统的性能检验

1.1 AD 检验

AD 统计量用于检验测量系统的正态性和独立性。经过查阅其它标准和该公式提出者的原始文献［14–15］，并进行数据验证，证实RB／T 141–2018 中的原公式有误，式(1)列出的是更正后的公式。

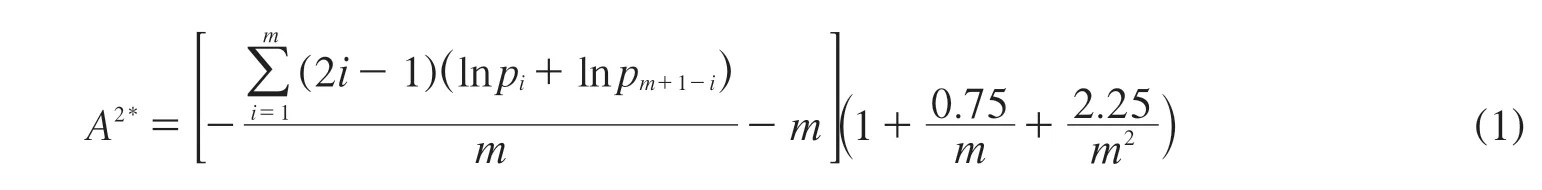
式中：A2*——A2*分别由正态性的统计量As2*(下标s表示标准差)和独立性的统计量AMR2*（下标MR 表示移动极差）表示，As2*＜1.0 且AMR2*＜1.0 时，表 明 在99%概率下接 受测量系统的正态性与独立性假设；

m——测量次数；

i——计算As2*时为测量结果按照升序排列的序号；计算AMR2*时为测量结果按照原始测量顺序排列的序号；

pi——第i 个测量结果的标准正态分布累积概率。

计算As2*时以根据贝塞尔公式计算的标准差s进行标准化；计算AMR2*时以按移动极差均值估计的标准差进行标准化。AD 检验的参数与计算见表1。

AD 检验电子表格只需在图1 中B 列输入测量数据，即可自动计算出As2*和AMR2*，结果分别显示在图1 中O2 和Q2 单元格。

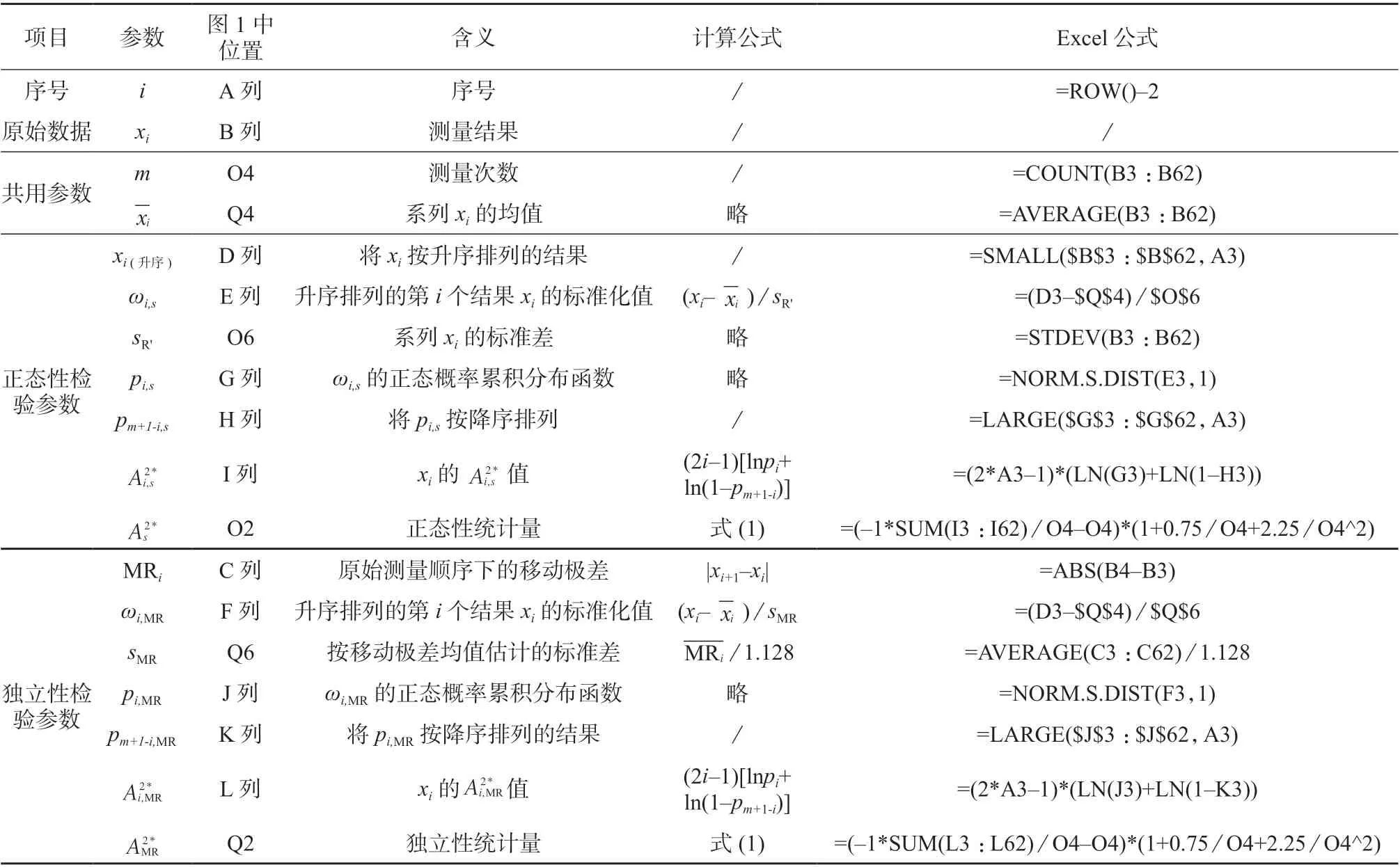
表1 AD 检验的参数与计算

图1 AD 检验电子表格界面示意图(原始数据引自RB／T 141–2018 中实例B.2.2)

1.2 h／k 检验

按公式(2)和(3)计算h／k 统计量：

式中： h——实验室间一致性统计量；

i——实验室序号；

bi——第i 个实验室的单元偏倚；

sx——样品水平下所有xi的标准差，其中xi为第i 个实验室的单元平均值。

k——实验室内一致性统计量；

si——第i 个实验室的单元标准差；

sr——重复性标准差。

当h／k 统计量未超出临界值，则在相应概率下接受测量系统一致性假设。h／k 检验参数与计算见表2。在h／k 检验电子表格（图2）中15 行以下区域录入测量结果，自动得h／k 统计量（图2中C2、C5）。

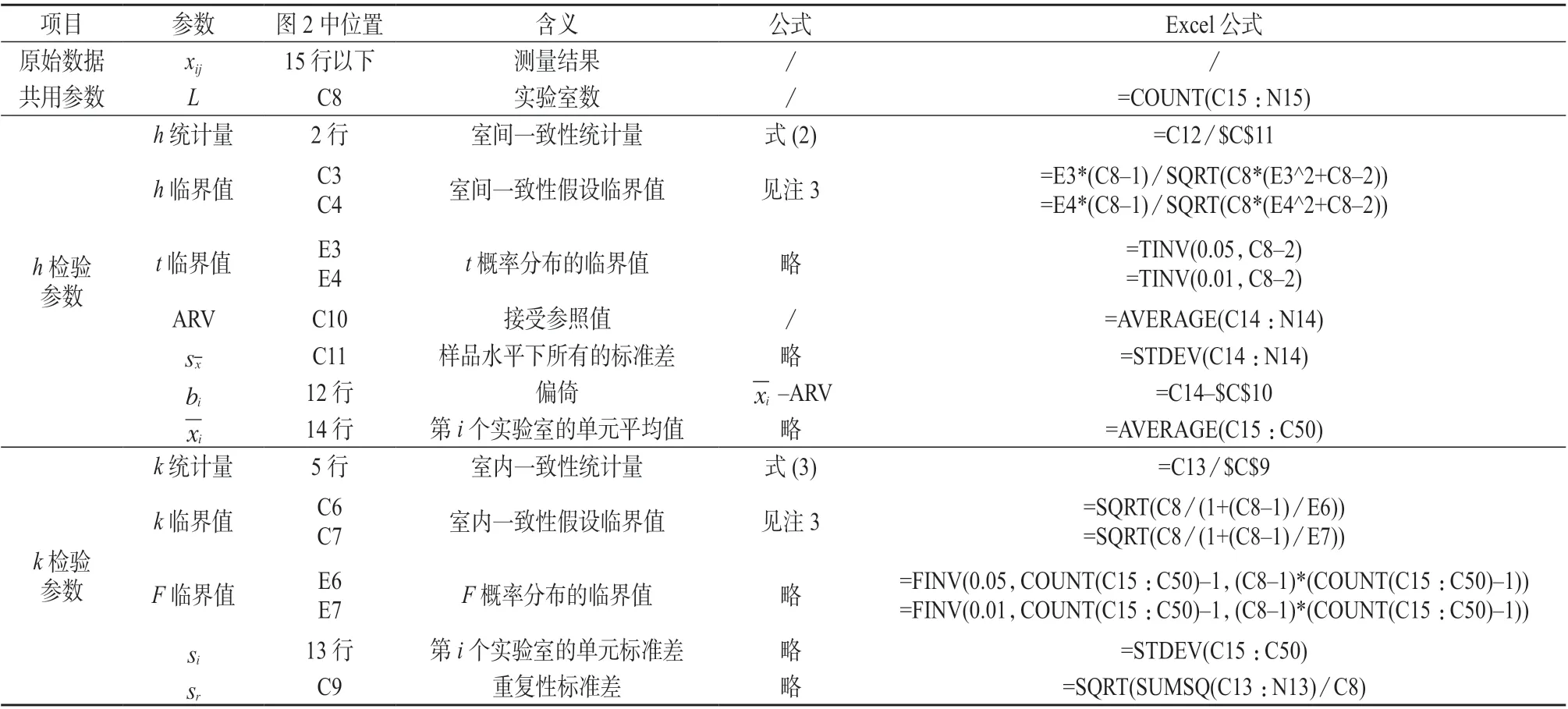
表2 h／k 检验的参数与计算

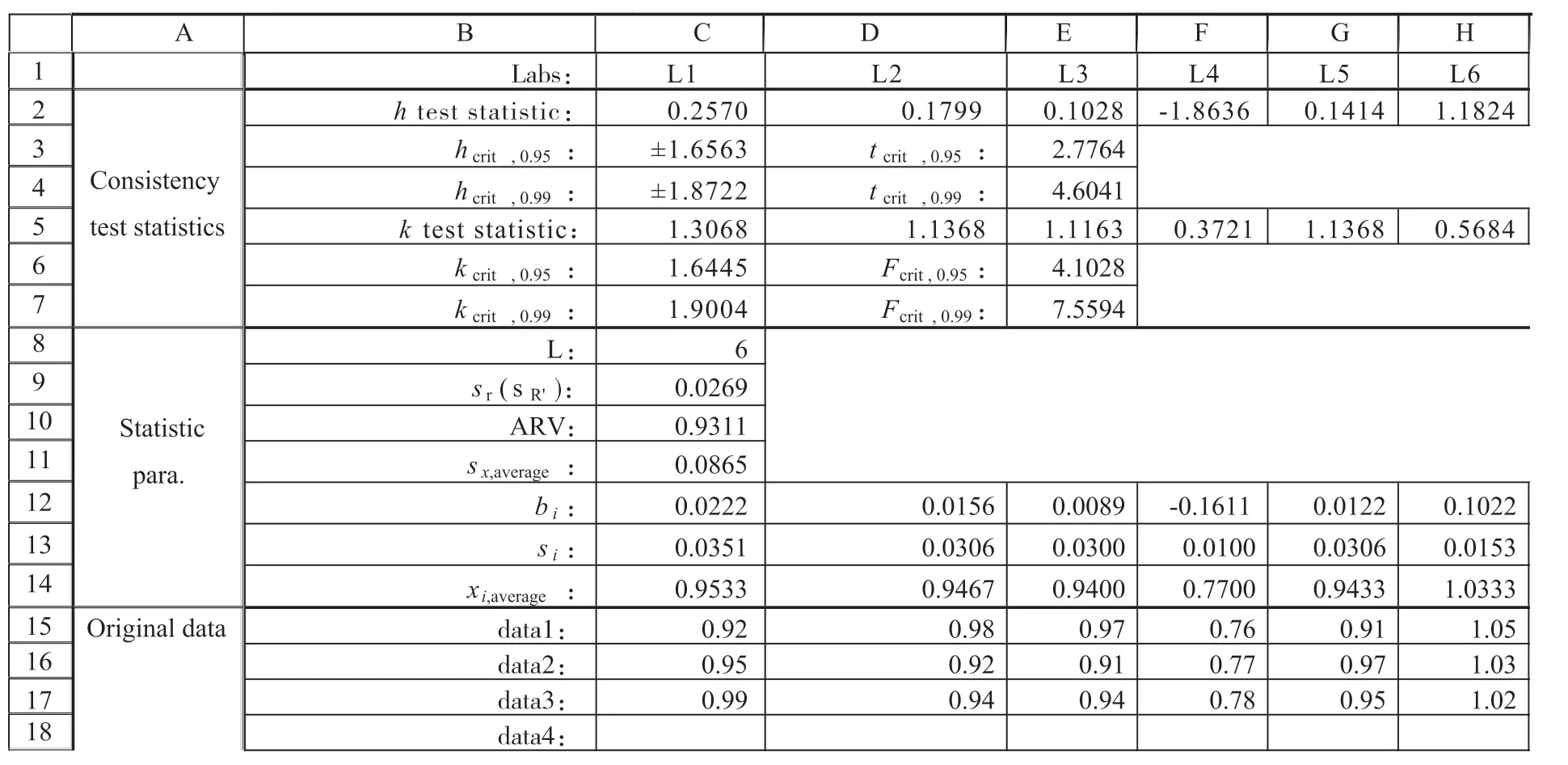
图2 检验电子表格界面示意图(原始数据引自RB／T 141–2018 中实例B.6.1)

2 期间精密度不确定度分量评定

根据稳定样品进行期间精密度不确定度分量评定，按式(4)进行计算：

式中：uR'——期间精密度不确定度分量；

sR'——期间精密度标准差。

按式(5)计算期间精密度不确定度分量评定：

式中：uR'(stand)——标准溶液样品的变异；

ur(range)——实际样品不同水平之间的变异(根据极差均值估计)。

根据非稳定样品进行期间精密度不确定度分量评定，按式(6)进行计算：

式中：uR'(bat)——其它程序给出或根据经验判断的不确定度。

期间精密度不确定度分量的组成与计算结果见表3 所示。

表3 期间精密度不确定度分量的组成与计算

期间精密度不确定度分量评定首先需要在其评定电子表格（图3）中的B2 单元格选取样品类型，然后在相应区域录入相应数据，即可根据上述公式计算出期间精密度不确定度的分量，结果显示在图3 中B10 和B11 单元格。

将RB／T 141–2018 中期间精密度不确定度分量的3种评定方式按表3 进行归纳可知，稳定样品分析和标准溶液样品分析中的分量1 sR'和uR'(stand)均为精密度数据，区别仅在于样品类型，因此作为同一输入量考虑（见图3 中B5 单元格）。标准溶液样品分析和非稳定样品分析中的分量2 是相同的（见图3 中B7 单元格）；分量3 仅在非稳定样品分析中出现。因此只需根据不同的评定方式选取相应的分量进行合成即可，Excel 电子表格设计时主要考虑的是公式和界面的整合优化（将3 种评定方式整合为1 个公式进行计算，并根据实际选择的评定方式输出相应的结果）以及易用性。

图3 期间精密度不确定度分量评定电子表格界面示意(原始数据引自RB／T 141–2018 中实例B.1.3，B.3.2，B.7.4)

图3 中B2 单元格设置了数据验证，只允许从“稳定样品”、“标准溶液样品”和“非稳定样品”中选择。当选择不同的评定方式时，无关信息均隐藏。动态隐藏效果是在条件格式中根据图3 中B2 单元格内容将无关单元格的字体颜色和填充色设置为背景色实现的。由于标准溶液样品分析和非稳定样品分析都涉及不同水平的样品，只能够用相对不确定度的形式给出，因此标准溶液样品分析和非稳定样品分析时只给出uR'，rel（输入量也要求为相对值），而稳定样品分析时则根据提供的sR'或sR'，rel给出相应的uR'或uR'，rel。

期间精密度（图3 中B4／B5）数据来自重复测量，可使用“AD 检验”电子表格中的sR'或sR'，rel；当涉及多个样本，需要计算合并样本标准差时，可使用“h／k 检验”电子表格中的sr；也可使用功能更加全面的“合并样本”电子表格（见图4），其功能如下：

（1）可基于极差法估计样本内标准偏差，再计算合并样品标准差；

（2）可计算复现性标准差；

（3）可根据自定义的各样本标准偏差计算合并样本标准差；

（4）适用于各样本中重复测量次数不相同的情况。所用的计算公式来自ISO 5725–2：2019［17］。

图4 合并样本电子表格界面示意图(原始数据引自RB／T 141–2018 中实例B.6.1)

样品不同水平之间的变异（图3 中B5）根据相对极差均值（图3 中B4）计算（=“B4／1.128”）。相对极差均值通常来自平行样品测定，根据各组平行测定结果的相对极差R 进行计算，可使用“平行样”电子表格（见图5）。该表格支持双样双针或双样单针测定的数据，可计算相对极差R 的算术平均值或RMS 均方根。uR'(bat)（图3 中B8）由其它程序给出或根据经验估计。

3 偏倚不确定度分量评定

根据核查样品（CS）进行偏倚不确定度分量评定，单水平按式(7)进行计算：

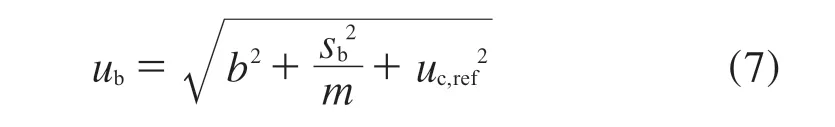
式中：ub——偏倚不确定度分量；

b——偏倚，测量结果均值与接受参照值ARV之差；

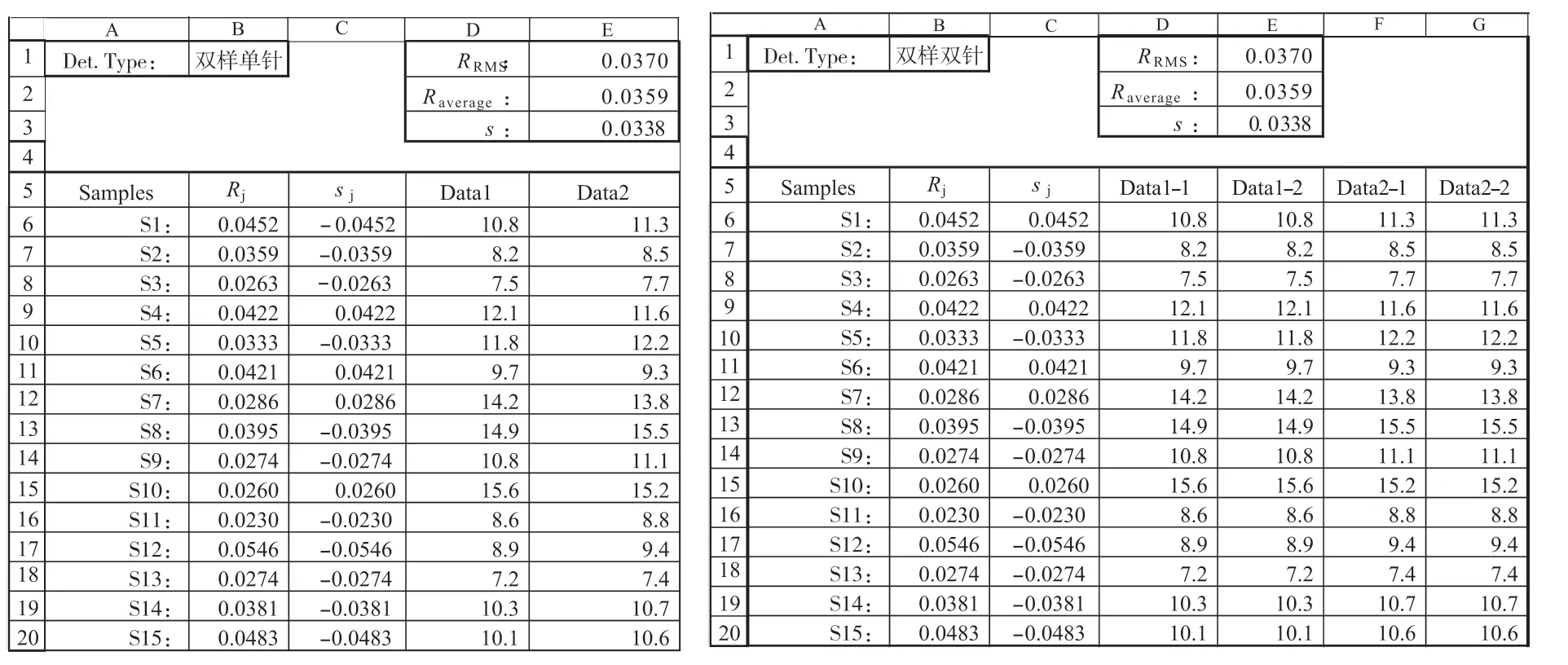
图5 平行样电子表格界面示意(原始数据引自RB／T 141–2018 中实例B.3.2)

sb——测量结果的标准差；

m——测量次数；

uc，ref——接受参照值ARV 的不确定度。

多水平按式(8)进行计算：

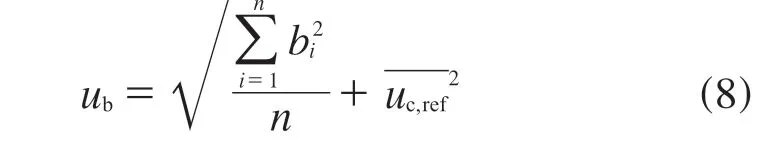
式中：bi——第i 个偏倚，其中i 为不同水平的序号；

uc,ref——各水平的接受参照值ARV 不确定度的平均值；

根据实验室间比对（ILC）与能力验证（PT）进行偏倚不确定度分量评定ub，单水平按式(9)进行计算，多水平按式(8)进行计算。

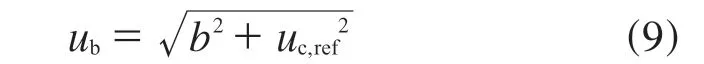
根据加标回收实验进行偏倚不确定度分量评定，多水平按式(10)进行计算：

期间精密度不确定度分量评定首先需要在图6中E2 单元格选取评定方式，在图6 中E3 单元格选取测量结果为“单水平”或“多水平”(根据加标回收实验评定时必须为多水平)，然后在相应区域录入相应数据，即可根据上述公式计算出偏倚不确定度分量，结果显示在图6 中E23、E24 单元格。

将RB／T 141–2018 中偏倚不确定度分量的评定方式按表4 进行归纳可知：

（2）分量2：仅在单水平CS 分析中出现，其中的sb即为sR'，可参照上文第2 部分使用“AD 检验”、“h／k 检验”或“合并样本”电子表格计算。

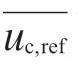
图6 中E2 单元格设置了数据验证，只允许从“CS”、“ILC 与PT”和“加标回收实验”中选择。图6 中E3 单元格设置了数据验证，只允许从“单水平”和“多水平”中选择。当选择不同的评定方式和样品水平时，无关信息均隐藏。动态隐藏效果是在条件格式中根据图6 中E2 和E3 单元格内容将无关单元格的字体颜色和填充色设置为背景色实现的。

选择“CS”分析时，需输入接受参照值ARV 的相关参数（单水平为图6 中E5：E7 区域，多水平为图6 中E5：N7 区域）和测得值（单水平为图6 中E15，多水平为图6 中E15：N15 区域）及相关参数（见图6 中E16：E18 区域）。

选择“ILC 与PT”分析时，需要选择ARV 类型（见图6 中E4），输入接受参照值ARV 的相关参数（见图6 中E5：N5 区域、E8：N10 区域）和测得值（见图6 中E15：N15）。

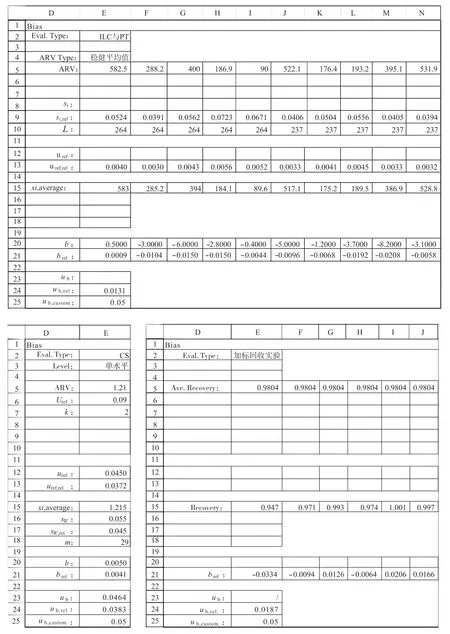
图6 偏倚不确定度分量评定Excel 电子表格界面示意(原始数据引自RB／T 141–2018 中实例B.1.4，B.2.3，B.3.3)

选择“加标回收实验”分析时，需要输入平均回收率（见图6 中E5：N5 区域）和回收率（见图6 中E15：N15 区域）。

加标回收实验分析只给出ub,ref，其余方式则根据提供的sR'(si)或sR',rel(si,rel)给出相应的ub或ub,rel。

4 扩展不确定度的计算

扩展不确定度按式(11)进行计算：

相对扩展不确定度按式(12)进行计算：

扩展不确定度(图7 中B23 单元格)和相对扩展不确定度(图7 中B24 单元格)对应的公式分别为“=IF(B2=" 稳 定 样 品"，2*SQRT(SUMSQ(B10，E23))，"")”和“=2*SQRT(SUMSQ(B11，E24))”。

为了提供更好的灵活性，表格中提供了自定义扩展不确定度Ucustom(图7 中B25 单元格)的合成计算，公式为“=2*SQRT(SUMSQ(B12，E25))”。在期间精密度和偏倚不确定度分量电子表格中分别输入不确定度分量UR',custom(图3 中B12 单元格)和Ub,custom(图6 中E25 单元格)时，可在图7 中得到计算结果。

表4 偏倚不确定度分量的组成与计算

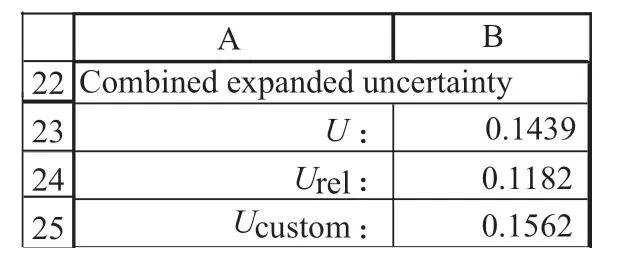
图7 合成扩展不确定度Excel 电子表格界面示意

5 结论

（1）建立了用于Top–Down 方法不确定度评定的Excel 电子表格，包含测量系统正态性、独立性和一致性检验、期间精密度不确定度分量评定、偏倚不确定度分量评定，以及不确定度的合成等功能。通过该电子表格计算得到的不确定度与测量系统性能检验统计量与RB／T 141–2018 中各实例的数据一致。

（2）AD 检 验、h／k 检 验 等 在 不 借 助SPSS、Minitab 等专业统计分析软件的情况下很难操作，但是在该电子表格中只需输入测量数据即可直接获得统计结果。复现性标准差、合并样本标准差等参数的计算非常繁琐，但是通过该电子表格也可直接获得计算结果。

（3）通过对RB／T 141–2018 标准中各计算公式的归纳分析，借助Excel 数据验证和条件格式，优化了该电子表格中的公式和界面，使得同一分量的不同方式评定可以在同一电子表格中进行，在功能完善的基础上进一步提高了易用性，简化了不确定度的评定过程，有利于Top–Down 技术的普及。