基于数值仿真的防波板焊接结构圆弧过渡分析

付雷，卢长煜，方洪渊

(1.徐州徐工环境技术有限公司,徐州 221001；2.哈尔滨工业大学，先进焊接与连接国家重点实验室,哈尔滨 150001)

0 前言

防波板焊接在水箱内部，是路面洗扫机械的重要部件。洗扫机械在路面行驶时，为抑制水箱中的水流对箱体侧壁的冲击作用，在水箱内部焊接钢板，即防波板，通常与水箱前后侧壁平行且居中放置，起到阻挡水流冲击的作用。值得注意的是，在水箱底板往往只有一个出水口，为保证水箱中存水可通过出水口全部流出，需要防波板的下方留出水流通道，现有的拱形通道在服役一段时间之后出现了疲劳失效裂纹，尤其是位于水箱底板的贯穿性裂纹直接导致水箱的泄露，需要进行维修。为了提高水箱的服役寿命，增加路面洗扫机械的市场竞争力，必须对防波板焊接结构设计优化。

在结构的拐角附近采用圆弧过渡是焊接结构优化的一种常用做法[1-6]，此法可以缓解拐角处由于几何不连续而造成的应力集中效应，从而降低峰值应力的幅值。显而易见，过渡圆弧设置的具体位置和半径取值，对缓解应力集中效应的作用效果有显著影响。

过渡圆弧的另外一个作用是将高应力区域从拐角附近转移至圆弧附近[7-9]。对于焊接结构，其焊接残余应力以拉伸应力为主，且峰值应力的幅值往往超过材料的屈服强度[4]，会在焊接完成后的服役过程中，与工作载荷联合作用，加速疲劳失效裂纹在焊接接头附近形成。然而在接头端部附近，过渡圆弧的设置，可显著降低工作载荷和焊接残余应力在该位置的作用程度，降低该位置的应力幅值，而此时的应力峰值位置将从焊脚附近转移至过渡圆弧内部，而圆弧形状的结构可促进集中的高应力向均匀的低应力转变[10]。因而文中将综合考虑圆弧位置和圆弧半径2种变量条件下，焊接残余应力与工作载荷对焊接结构的应力集中效应的影响规律，并根据影响规律给出圆弧设置的合理建议，如此方能使防波板焊接结构的抗疲劳性能得到有效提高。

1 原结构的仿真

1.1 仿真模型的简化

图1为防波板结构的原模型。防波板位于路面洗扫机械的水箱内部，如图1a所示，由一块独立的钢板构成，钢板四周与水箱箱体采用焊接相连，焊道为单面满焊。防波板中间设置人孔，可供人员进出；下方靠近中间的位置，设置拱形通道，以方便水箱中的存水从出水口流出。在拱形通道附近，防波板与水箱底板连接焊道端部附近出现了疲劳失效裂纹，将防波板的承载模型进行合理地简化，以降低有限元仿真的计算量。由于疲劳失效的启裂点位于拱形通道两侧的焊道端部附近，因而焊道端部附近结构，按照实际尺寸构建由立板和底板焊接连接的仿真模型，如图1b所示，对应的有限元模型如图1c所示，另一方面对远离疲劳裂纹位置的箱体侧壁和防波板进行简化，箱体侧壁的主要作用是对整个防波板和箱体底板的位移进行限制，如图1d所示，对底板的侧边施加位移边界条件。由于文中仅对防波板拱形通道附近的局部焊接结构进行了仿真，分析其失效原因，给出规律性的结论，并非针对某个确定的防波板结构，因而无需实测的数据进行验证仿真结果的准确性，仅需通过理论判定应力分布的合理性即可。

以疲劳失效裂纹为研究核心，对疲劳失效有贡献的载荷分为工作载荷与焊接残余应力2种，其中工作载荷主要为水流对防波板的冲击作用，与箱体和水流的加速度相关，为简化仿真分析过程，将冲击载荷设置为路面洗扫机械紧急制动条件下水流对防波板冲击的最大值，其幅值为4.0 kPa，作用在防波板侧面，与焊道分别处于防波板(立板)的两侧，如图1c和图1d所示。

对于防波板的焊接结构，其焊道设置和焊接方向如图1b所示，实际施焊时，采用混合气体保护焊(MAG焊)，立板和底板的材质均为Q345钢板，立板的板长400 mm，板宽300 mm，板厚为3 mm；底板的板长500，板宽450 mm，板厚为3 mm；焊道长度300 mm，焊接保护气为80%Ar+20%CO2混合气体，焊接时保护气流量为15～20 L/min，焊接电流为180 A，电弧电压为20 V，焊接速度为5 mm/s，采用牌号为WH50-6的镀铜低合金钢焊丝，焊丝直径1.2 mm，仿真计算时忽略焊缝与母材之间的热-物理性能差异。

采用有限元软件Hypermesh进行网格划分，划分结果如图1c所示，焊道为角焊缝，焊脚为边长4 mm×4 mm的等腰直角三角形，为减少数值仿真计算量，整个模型仅在焊缝附近采用较为密集的网格单元，以疏密过渡的方式划分整个模型的网格，模型共计网格单元14 345个，单元节点21 772个，采用有限元仿真软件MSC.Marc施加边界条件，并进行计算和分析。

图1 防波板结构的原模型

焊接热源采用双椭球热源模型，其热源分布表达式参见文献[11]，此处不再多述。对于焊接热源参数，其宽度为6 mm，深度为4 mm，前轴长为3 mm，后轴长为10 mm，热源有效系数为0.7，模型初始温度为20 ℃，模型与空气的对流换热系数为40 W/(m2·K),忽略焊缝与母材成分和力学性能的差异，因而模型中所有的网格单元均设定为Q345B钢材的力学性能参数和热物理性能参数[4,7,10]，焊接完成后空冷30 min，随后施加载荷边界条件，有限元计算和输出模型的等效应力分布。

1.2 仿真结果

为了明确工作载荷与焊接过程对防波板焊接结构的影响规律，分别计算工作载荷和焊接过程及焊后加载共3种载荷模型的等效应力分布，有限元仿真结果如图2所示。

图2 有限元仿真结果

当模型仅在焊接残余应力作用时，其等效应力分布如图2a所示，峰值应力为349.6 MPa，比母材屈服强度值略高，其高应力主要分布于焊道两侧附近，而在焊道收弧位置，高应力区域的面积较大，该区域包括了疲劳裂纹的启裂点，所以焊接残余应力可能对疲劳失效的开裂提供动力；当工作载荷单独在模型时，其等效应力分布如图2b所示，峰值应力为218.5 MPa，高应力集中分布在焊道的收弧点附近的立板上，与疲劳失效位置相近，说明工作载荷可能会促进裂纹形成和扩展；焊接残余应力与工作载荷的叠加效应如图2c所示，其峰值应力为371.3 MPa，该应力幅值高于焊接应力或者工作应力的最大值。

1.3 失效分析

按照图2c中的箭头方向，沿着所示路径A和路径B依次拾取工作应力、焊接应力及焊后加载的叠加应力的计算数据，2种路径上3种应力的对比结果如图3所示。

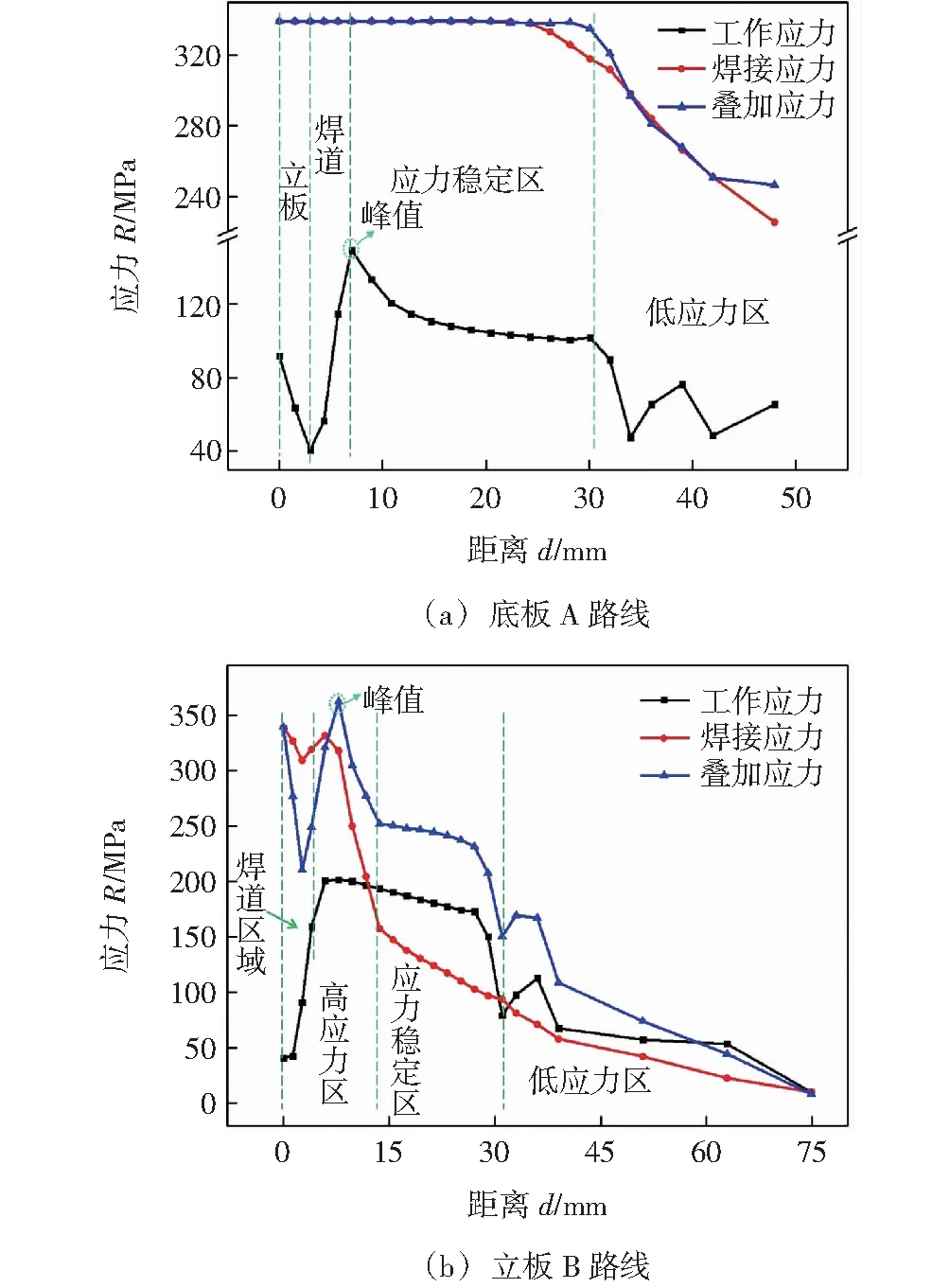
图3 仿真结果分析

对于底板的拾取路径A，工作应力的幅值明显低于焊接应力和叠加应力，在焊道外侧的边界位置达到峰值，仅为149.4 MPa；焊接应力在焊道附近达到稳定值，其幅值等于材料的屈服强度，即存在应力屈服区，屈服区长度为24 mm；叠加应力的应力屈服区长度略大于焊接应力，达到28 mm，说明是工作载荷加剧了焊接应力的承载效果，增加了应力屈服区域的长度，是该位置疲劳失效的主因。

对于立板的拾取路径B，沿拾取方向依次分为高应力区、应力稳定区、低应力区共3个区域，高应力区包含焊道附近区域，总长为13.6 mm，该区域的叠加应力在焊道外侧的3.4 mm位置达到峰值，峰值应力幅值为362.3 MPa，高于材料的屈服强度，该位置与疲劳裂纹启裂点重合，说明焊后加载的工作载荷和焊接残余应力相互叠加，促使疲劳裂纹失效发生。另外，立板拾取路径上工作应力与焊接应力之间的分布趋势差异较为明显。焊接应力在立板的焊道外侧附近4 mm区域内的应力水平较高，而在距离大于4 mm的区域内，随着距离焊道的长度增加，应力水平急速下降，并且在应力稳定区低于工作应力。立板上工作应力在焊道位置的应力水平较低，这是焊道填充金属对立板的支撑作用所致，在远离焊道相当长的距离内，工作应力趋于稳定。 工作应力与焊接应力在疲劳失效位置均接近应力的最大值，是导致该位置的叠加应力幅值达到顶峰的主要原因。

2 圆弧优化的仿真分析

为提升防波板焊接结构的疲劳性能，采用立板根部圆弧过渡的优化设计，并采用有限元方法分析优化设计的合理性。

2.1 构建优化模型

由于焊道端部结构的应力集中程度对疲劳裂纹的产生与否具有决定性影响，因而文中在立板的根部位置，采用圆弧过渡的方法降低裂纹失效位置的应力集中程度，以提高焊接结构的抗疲劳失效性能。

装配示意图如图4所示。在立板的左侧边界，距离底板上表面的长度为d的位置设置半圆弧，圆弧半径为r，距离d和半径r均为变量，并通过调整这两个变量的取值，分析其对焊接结构应力分布的影响规律，以期获得对降低应力集中效应最为有利的结构形式。

图4 装配示意图

以d= 12 mm和r= 20 mm为例构建优化模型，划分单元网格结果如图5所示，优化模型在焊道附近的网格单元与原模型相同，同样采用疏密过渡方式划分网格，模型共计网格单元15 568个，单元节点23 625个，对于优化模型的焊接热源模型和边界条件，均与原模型相同。

图5 仿真模型

2.2 仿真结果

为了与原模型的仿真结果相比较，分别计算优化模型的工作载荷和焊接过程及焊后加载3种载荷模型的等效应力分布，如图6所示。

当优化模型仅在焊接应力作用时，其等效应力分布如图6a所示，与原模型相比，高应力都分布在焊道两侧位置，且高应力区域在焊道收弧附近的面积都比较大。虽然优化模型的焊接应力峰值略高于原模型，但是在立板的焊道端部附近，尤其是靠近过渡圆弧的区域，应力水平得到较大程度的降低，对该位置的应力集中效应则会有明显的改善。然而在过渡圆弧区域则形成一个新的应力集中区域，位于圆弧的下半段位置。

当工作载荷单独在优化模型时，等效应力分布如图6b所示，其峰值应力为244.6 MPa，高于原模型的218.5 MPa，位于立板的过渡圆弧上，与附近的焊接应力形成的应力集中区位置相近，可能会相互叠加进一步促进疲劳裂纹形成和扩展。

对优化模型的焊接和焊后加载过程进行仿真计算，得到的焊接残余应力与工作载荷的叠加效应如图6c所示，其峰值应力为370.7 MPa，略低于原模型的371.3 MPa，同样高于焊接应力或者工作应力的最大值。值得注意的是，在过渡圆弧位置，高应力区的范围，比之焊接应力和工作应力，有较大程度的增加，有可能导致屈服范围的增加，致使应力集中效应加大，使该处成为新的疲劳失效危险点。

图6 有限元计算结果

3 圆弧优化的影响规律分析

对于模型的优化效果，文中通过调整过渡圆弧距离和半径这2个变量的取值，分析其对焊接结构应力分布的影响规律，为优化模型的参数选择提供一些理论依据。

3.1 圆弧距离的影响规律

为了明确圆弧距离d对应力分布的影响规律，将另一个变量(半径r)设为定值，此处设定所有的圆弧半径均为20 mm，按照图5c中箭头方向，沿着所示路径I，II和III，依次拾取工作应力和焊后加载的叠加应力在不同d条件下的结果，3种路径的应力对比结果，分别如图7、图8和图9所示。

对于底板的拾取路径I，不同距离d条件下，工作应力的变化规律如图7a所示，随着距离的不断增加，工作应力的峰值应力随之提高，说明过渡圆弧距离焊道越近，底板所承受的工作载荷越小；焊后加载的叠加应力分布见图7b，叠加应力的高应力区幅值普遍高于材料的屈服强度，存在屈服区域，而对于不同的距离d，总体而言，随着距离的降低，屈服区的长度随之减少。对于焊道附近区域，其焊接残余应力的幅值通常达到屈服状态，随后进行焊后加载，该区域的应力重新分布。由于塑性变形的不均匀性和加工硬化指数，以及弹塑性力学模型的影响，导致屈服区的应力分布并不均匀，此理论可以解释图7b中焊道附近的应力分布呈现起伏不平的现象。

图7 底板的路线I计算结果

对于立板的拾取路径II，工作应力的对比结果如图8a所示，焊后加载的叠加应力结果如图8b所示，拾取路径II的长度与距离d各自相等。对于路径II的工作应力，其分布状况如图8a所示，工作应力在焊道外侧2 mm的位置达到峰值，并且随着距离d的增加，峰值应力的幅值随之提高，说明过渡圆弧距离焊道越近，立板在路径II的工作应力越小；对于路径II，其焊后加载的叠加应力分布状况如图8b所示，当d小于12 mm时，焊道外侧的应力水平低于材料的屈服强度，当d大于15 mm时，焊道外侧出现了一定宽度的屈服区，并且随着d取值的增加，屈服区的长度随之增加，说明过渡圆弧距离焊道越近，路径II应力水平越低，发生疲劳失效的可能性越小。

对于立板的拾取路径III，工作应力的对比结果如图8a所示，焊后加载的叠加应力结果如图8b所示，路径III从过渡圆弧的下方端点开始，沿着半圆弧拾取，到过渡圆弧的上方端点结束，拾取路径的长度转换成角度，以方便观察和对比。

图8 立板的路线II计算结果

对于路径III的工作应力，其分布状况如图9a所示，工作应力的峰值位置均在50°～ 90°范围内，并且随着d的增加，峰值应力的幅值随之降低，说明过渡圆弧距离焊道越近，圆弧的工作应力峰值越大。由于原模型的峰值应力位于焊道附近，所以过渡圆弧距离焊道越近，高应力区迁移至圆弧更加容易，因而致使圆弧的峰值应力幅值增加。

对于路径III的叠加应力，其分布状况如图9b所示，图中所列的曲线均包含两个峰值位置，两个峰值位置相距不远，均分布在30°～ 90°范围内，两个峰值之间的区域均达到屈服状态，以每条曲线中两个峰值的中间位置为参考点，随着d取值的增加，参考点向角度变小的方向偏移。

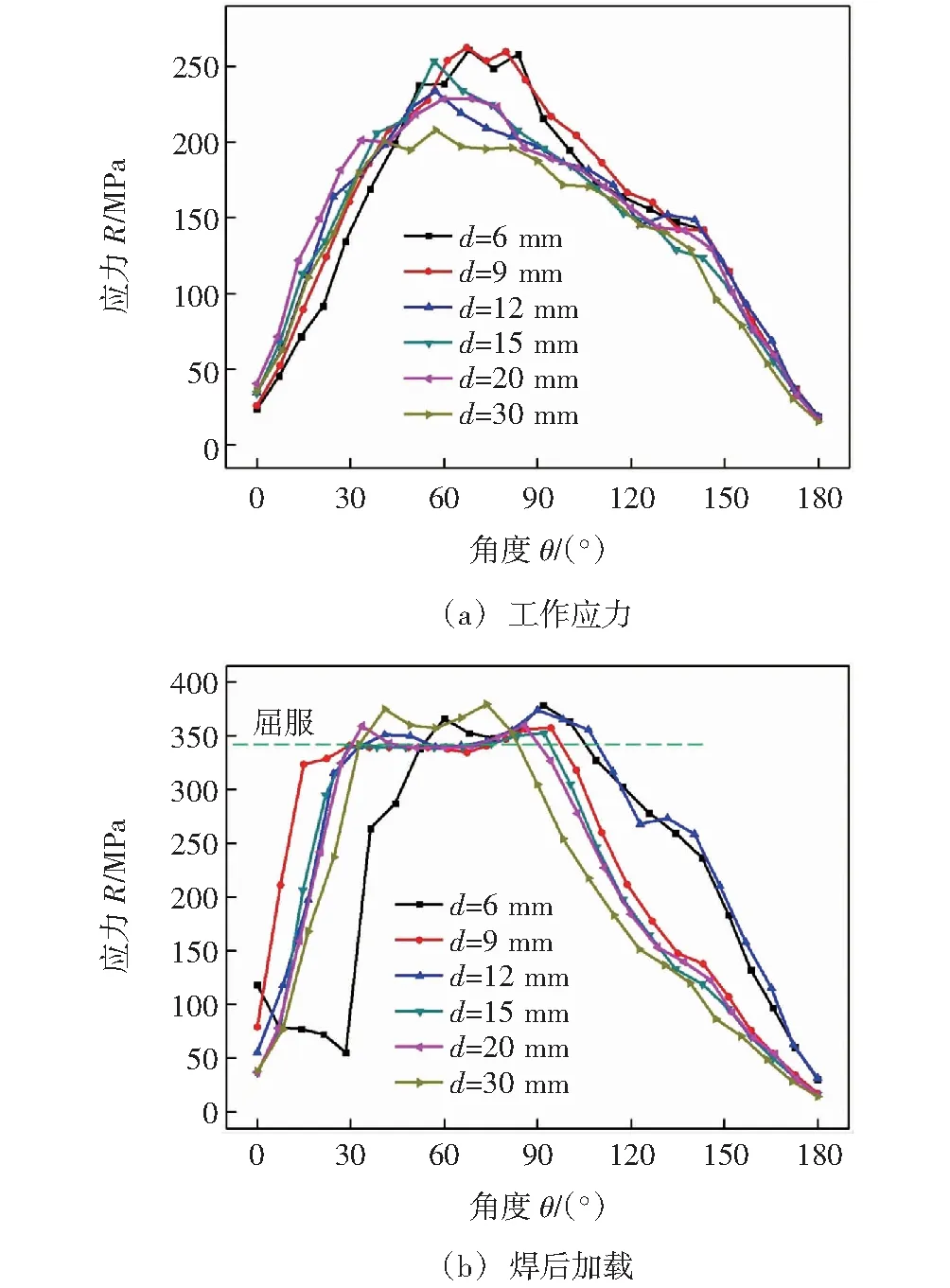
图9 立板的路线III的计算结果

3.2 圆弧半径的影响规律

为明晰圆弧半径r的影响规律，将另一个变量(半径d)设为定值，此处设定所有的变量d均为12 mm，按照图6c中箭头方向，沿着所示路径I，II，和III，依次拾取工作应力和焊后加载的叠加应力在不同半径r条件下的计算结果，3种路径的对比结果分别如图10、图11和图12所示。

对于底板的拾取路径I，不同圆弧半径r条件下，工作应力的变化规律如图10a所示，随着半径r的不断提高，工作应力的峰值应力随之降低，说明过渡圆弧半径越大，底板所承受的工作载荷越小；焊后加载的叠加应力分布如图10b所示，叠加应力的高应力区幅值普遍高于材料的屈服强度，存在屈服区域，当圆弧半径r小于20 mm，屈服区长度变化不明显，而当圆弧半径r等于30 mm时，屈服区长度的降低较为明显。

图10 底板的路线I计算结果

对于立板的拾取路径II，工作应力的对比结果如图11a所示，焊后加载的叠加应力结果如图11b所示，拾取路径II的长度与距离d相等，总长均为12 mm，包含焊道的长度4 mm。

路径II的工作应力分布状况如图11a所示，工作应力在焊道外侧2 mm的位置达到峰值，随着圆弧半径r的增加，应力水平随之降低；路径II焊后加载的叠加应力分布状况如图11b所示，当r大于5 mm时，焊道外侧的应力水平均低于材料的屈服强度，并且随着r取值的增加，应力水平随之降低，说明过渡圆弧对底板的应力集中效应有明显的降低作用，随着圆弧半径的增加，应力的降低作用则越明显。

图11 立板的路线II计算结果

立板拾取路径III工作应力的对比结果如图12a所示，焊后加载的叠加应力结果如图12b所示，从过渡圆弧的下方端点开始拾取，将拾取路径的长度转换成角度，以方便观察和对比。对于路径III的工作应力，其分布状况如图12a所示，工作应力的峰值位置均在50°～90°范围内，的位置达到峰值，并且随着半径r的提高，峰值应力的幅值随之降低。过渡圆弧半径越大，圆弧周长越长，因而增加承载区域，导致圆弧处应力幅值的降低。

对于路径III的叠加应力，其分布状况如图12b所示，所列曲线均包含2个峰值位置，2个峰值位置相距不远，均分布在30°～ 120°范围内，2个峰值之间的区域为曲线的高应力区，以每条曲线中2个峰值的中间位置为参考点。随着r取值的增加，参考点向角度变小的方向偏移。值得注意的是，图12b中圆弧半径为30 mm的曲线，其叠加应力的幅值均低于材料的屈服强度，说明参数为d=12 mm且r=30 mm的优化模型，在焊后承受水流冲击时，底板的路径III并没有达到屈服状态，因而底板的疲劳失效模型，有从低周疲劳失效模型向高周疲劳失效模型转换的趋势，使得疲劳服役的寿命得到明显提升。

图12 立板的路线III计算结果

3.3 圆弧承载特点

以2种优化模型参数变量为例，沿拾取路径III分别提取2个模型的工作应力和焊接应力及叠加应力，对比分析过渡圆弧处承载特点。此处选择参数d为12 mm，参数r分别取值20 mm和30 mm，与之相对应的应力分布结果如图13所示。

在图13a中，圆弧半径为20 mm，其工作应力的峰值位置与焊接应力的峰值位置之间的间距为2.9 mm，该间距取值较小，造成该区域的焊后加载的叠加应力水平得到大幅度提高，超过了屈服强度，并通过扩张屈服范围而降低应力水平，因而造成叠加应力曲线的屈服长度增加，增加至22.8 mm。

在图13b中，圆弧半径增加至30 mm时，其工作应力的峰值位置与焊接应力的峰值位置之间的间距为7.6 mm，此间距的取值明显大于图13a中的2.9 mm，因此该区域的焊后加载的叠加应力水平，与图13a中曲线相比，得到大幅度降低，且最大值也可低于材料的屈服强度。叠加应力的曲线中，2个峰值位置的间距为15.2 mm，小于图13a中的间距(20.0 mm)，说明圆弧半径的增加，导致圆弧处应力水平的降低，即使是峰值应力也可降低至屈服强度以下，提升圆弧处疲劳服役的寿命。

图13 立板路线III的应力对比

3.4 优化原则的讨论

在焊接结构拐角处，采用圆弧过渡的优化方式，可使原结构疲劳失效危险点的应力集中程度得到有效降低。而过渡圆弧的位置和半径，对应力集中效应的缓解效果有明显的影响规律。在底板的危险点附近，圆弧距离焊道越近或者增加圆弧半径取值，工作应力幅值都会随之降低，导致该区域焊后加载屈服范围的缩小，降低了应力集中程度；在立板的危险点附近，即焊道外侧边界，随着过渡圆弧的靠近，工作应力和焊后加载的叠加应力都有大幅度降低，在图8b中，当圆弧距离焊道低于8 mm时，该位置叠加应力的幅值低于材料屈服强度。

值得注意的是，虽然靠近焊道的过渡圆弧，可以降低立板危险点的应力集中，但是在圆弧上也会出现新的高应力区，成为新的疲劳失效危险点。为了提高圆弧处危险点的疲劳服役寿命，需要降低应力水平和应力集中程度。文中的仿真数据表明，通过增加圆弧半径的取值，可有效增加工作应力峰值和焊接应力峰值之间的间距，从而明显降低焊后加载的叠加应力峰值及高应力区范围(图13)，当圆弧半径增加至30 mm时，圆弧处危险点应力水平则低于材料的屈服强度。

对于疲劳失效的形式而言，当危险点的应力水平高于材料的屈服强度时，其载荷称为低周疲劳载荷，疲劳失效破坏的循环次数往往低于1×104～ 1×105，是设计中需要极力避免的；而当危险点的应力水平低于材料的屈服强度时，称为高周疲劳载荷，疲劳失效破坏的循环次数比之低周疲劳有大幅度的提高。因此，文中对焊接结构的优化设计目的，在于降低疲劳危险点的应力幅值，使之降低到屈服强度以下，以提升服役的寿命。

焊接结构的特殊性在于焊道附近焊接残余应力的幅值较高，在焊后服役时，焊接残余应力与工作载荷相互叠加，使得叠加应力的集中效应加重[12-13]。文中通过过渡圆弧，将焊接残余应力与工作应力的峰值位置间距加大，以降低应力的叠加效应，以至于低于屈服强度，如此则达到设计优化的目标。

4 结论

(1)原有的防波板焊接结构，由于工作载荷与焊接残余应力的叠加效应，在底板和立板的焊道附近位置，存在应力集中问题，峰值应力达到屈服状态，是造成疲劳失效的主要原因。

(2)在立板与底板连接的拐角处，采用圆弧过渡的优化方式，可使原结构疲劳失效危险点的应力集中程度得到有效降低，但是圆弧的高应力区会成为新的疲劳失效危险点。

(3)对于底板的疲劳失效危险点，缩短圆弧与焊道的距离或者增加圆弧的半径，都会降低工作应力的幅值，缩小焊后加载屈服范围，达到提高底板服役寿命的目标。

(4)立板的疲劳失效危险点在焊道外侧，增加圆弧半径，可同时降低焊道附近和圆弧两处位置的应力幅值，原因在于其工作载荷和焊接应力的峰值位置并不重合，从而降低焊后加载的叠加效应。