基于经验模态分解-小波包变换的表面肌电信号手势识别

冯凯，董秀成，刘栋博

西华大学电气与电子信息学院，四川成都611730

前言

手部运动时的表面肌电信号（surface Electromyography Signals,sEMG）是上肢肌肉收缩过程中，大量运动单元动作电位经肌肉、皮下组织和皮肤的传导叠加，最终反映在皮肤表面的综合电效应［1-3］。通过粘贴在皮肤表面的电极来采集不同手势下的sEMG，具有无创伤性的特点，已被广泛应用于手语识别、假手控制和手部康复机器人控制等领域［4］。sEMG 信号的采集、降噪、数据分割、特征提取、特征选择与降维和分类器的设计等各个环节均已成为国内外研究人员争相研究的热点，并且取得了不错的成就。机器学习广泛用于解决基于sEMG信号的手势识别问题，最常见的手势识别方法包括线性判别分析（Linear Discriminant Analysis,LDA）［5］、支持向量机（Support Vector Machines,SVM）［6］、K-近邻（K-Nearest Neighbor,K-NN）［7］、随机森林（Random Forest,RF）［8］、决策树（Decision Tree,DT）［9］、人工神经网络（Artificial Neural Networks,ANN）［10］、卷积神经网络（Convolutional Neural Networks,CNN）［11］等。

sEMG 是一种非线性非平稳的生物电信号［12］，同大部分涉及生物医学信号的模式识别应用一样，为了得到好的识别效果和减少数据冗余，需要对sEMG信号进行预处理和特征提取。许多研究人员已经开始研究sEMG信号的特征，如时域特征［13］、频域特征、时频特征［14］和高阶统计量［15］，研究人员也开始研究一些不属于时域和频域的新特征，如非线性特性和分形特征［16］，自回归模型分析［17］也是获取信号特征的一种常用方法。Sui 等［1］从sEMG 中提取小波包系数的能量和方差作为特征，并结合改进支持向量机（Improved Support Vector Machine,ISVM）和粒子群算法（Particle Swarm Algorithm,PSO）进行手势分类，平均识别率为90.66%。Wu 等［18］提出基于单通道sEMG 包络信号时域特征提取方法，并且使用改进的K-NN 算法和软缘SVM 算法来完成5 种类型手势的分类，平均识别率为80%。Liang 等［19］通过传感器同时采集原始肌电信号和肌电信号包络线并提取时域、频域以及时-频域特征来提高识别正确率，识别正确率达到95%。Narayan等［20］利用原始sEMG特征的一阶微分得到4 种新的时域特征，识别正确率为86.7%。都明宇等［21］提取时域和频域特征，通过改进决策树SVM 对手势动作进行分类，平均识别率达88.9%。宋佳强等［22］将sEMG 信号和其高阶差分信号的能量谱进行组合，使不同手势动作的特征之间更具有差异性，识别正确率达到94.5%。于亚萍等［23］将基于DB、Dmey和Bior 3种小波提取的肌电信号特征进行融合，采用融合处理后的特征手势识别正确率达到95.7%。

上述研究采用的信号分析方法，在分析非线性非平稳信号时，需要假设信号局部平稳，基函数也比较固定，缺乏自适应或自适应差，无法充分体现sEMG 的本质特征，造成信号的可分类性差，手势识别准确率较低。针对上述不足，本文提出一种基于经验模态分解（Empirical Mode Decomposition,EMD）和小波包变换（Wavelet Packet Transform,WPT）的sEMG手势识别模型，先采用EMD将信号平稳化，选择与原始信号有较高相关性的固有模态函数（Intrinsic Mode Function,IMF）进行选择WPT，并提取小波包系数特征形成特征向量，通过SVM 和LDA 两种分类器对12 种手势进行识别，其流程如图1所示。

图1 肌电信号手势识别流程图Fig.1 Flowchart of hand gesture recognition by electromyography(EMG)signal

1 试验设计与数据采集

1.1 试验设计

选择12种生活中常用的手势（图2），编号分别为手势1～12。采集过程中每个动作重复12 次，每次动作持续大约2 s，每次动作完成后休息2 s，每种动作完成后休息1 min 避免手臂肌肉疲劳。随机选择其中8 次作为训练样本，剩余4 次作为测试样本。试验共采集数据2 160 组，其中选择1 440 组为训练样本，剩余720组为测试样本。

1.2 数据采集

试验所用的采集装置是美国Delsys 公司生产的Delays Myomonitor IV（Delays Inc.）表面肌电采集系统，如图3所示，共包含有8 个电极，实验过程中只使用1～4号电极，系统采集频率为2 000 Hz，大于sEMG信号最大频率的两倍，符合奈奎斯特采样定理。15名年龄在20～24 岁且没有神经或肌肉疾病的受试者自愿参加试验，并且在试验前已经熟悉试验流程。通过比较确定采集的肌群分别为掌长肌（1 号电极）、桡侧腕曲肌（2 号电极）、尺侧腕曲肌（3 号电极）和指伸肌（4 号电极），4 个电极放置位置如图4所示，在贴电极之前用酒精清洁手臂皮肤。手势1 的4 个通道的部分数据如图5所示。

图2 手势动作示意图Fig.2 Schematic diagram of hand gestures

图3 表面肌电采集系统Fig.3 Surface EMG acquisition system

图4 电极放置位置示意图Fig.4 Schematic diagram of electrode placement

图5 手势1的4通道肌电信号Fig.5 Four-channel EMG signal of hand gesture 1

2 数据预处理与特征提取

2.1 数据预处理

原始sEMG 的噪声成分较为复杂，采集过程中sEMG 信号容易受到外部环境的干扰，运动伪影、基线偏移和工频干扰都可能导致sEMG 信号的失真，从而导致分类效果差［24］，采用通带频率为10～500 Hz的带通滤波器进行滤波，每个信道中检测到的sEMG信号在不同的手势动作中的强度不同，但信号表现出良好的同步性。如果相关肌肉不收缩，则sEMG信号在测试前表现出稳定的低振幅信号；相反，在执行动作的过程中信号发生了显著变化［25］。本文采用短时能量和能量阈值T来探测动作的开始和结束并进行数据的分割。短时能量计算公式如式（1）所示：

其中，x(t)表示连续的sEMG信号，x(n)表示其离散序列，TS表示连续信号中所取的时间窗宽度，其取值不超过300 ms，N表示其对应的序列长度。阈值T的可以取几个不同的受试者静止时能量的平均值。虽然不同受试者的能量值不完全相等，但在静止时sEMG信号中的能量偏差不会太大［26］。阈值T计算公式如式（2）所示：

其中，Eq表示静止时采集的sEMG信号中的能量值，n表示采集的静止信号次数。当检测到某一连续时间段中的短时能量值持续大于阈值T，则认为该段时间为动作段，如果某一时间段的短时能量持续小于阈值T，则认为是静止段，从而判断动作的起始位置。

EMD 依据数据自身的时间尺度特征来进行数据分解［27-29］，无需设置基函数，这与傅里叶变换和小波变换建立在先验性谐波基和小波函数上的分解有本质上的差别，并且sEMG 信号经EMD 分解后变得平稳，有利于进行特征提取。EMD 方法分解信号基于以下3 条假设［30］：（1）信号至少具有一个极大值点和一个极小值点。（2）把相邻极值点之间的时间间隔定义为特征时间尺度。（3）当信号没有极值点而仅有拐点时，那么在对其分解之前首先将拐点微分一次或者多次以获得极值点，然后对所得结果进行积分就得到相应的分量。

EMD 作为一种自适应非线性滤波器，将信号分解为若干IMF，其中IMF 代表一个简单的振荡函数，满足两个条件［27］：（1）过零点数和局部极值数相等，或相差一个。（2）由局部最大和局部最小包络的平均数定义的局部平均数等于零。

对于待处理sEMG 信号x(t)，由于其非线性和非平稳特性，满足EMD 分解信号的3 条假设，不同的sEMG 信号均可以分解形成若干具有不同特征尺度的特征模态函数。进行EMD分解的步骤如下。

（1）确定sEMG 信号x(t)的所有局部极大值和极小值点，若没有极值时，找出其拐点进行微分直到获得极值点。

（2）用插值法将所有极小值点连接起来形成下包络，同理将极大值点连接起来形成上包络，使所有数据点处于两条包络线之间，结果如图6所示。

（3）计算平均包络曲线m(t)，结果如图7所示。

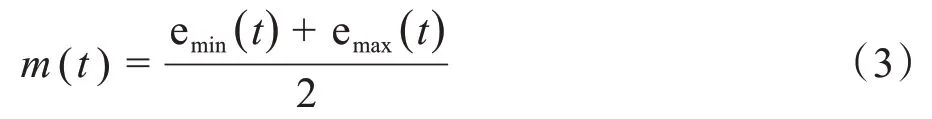
（4）提取IMF 成分，从待处理信号x(t)减去平均包络线，结果如图8所示。

图6 上下包络线Fig.6 Upper and lower envelope curve

图7 平均包络线Fig.7 Average envelope curve

图8 EMD分解过程及结果Fig.8 Empirical mode decomposition process and results

（5）从待处理信号中分解出第一个IMF 后，得到剩余值序列作为新的待处理信号，重复上述步骤，直到满足停止准则后结束分解。在实际中，上述过程需要通过一个检测过程，检测是否满足IMF 的两个条件，若不满足，将作为待处理的信号重复1～4步，直到确认是一个IMF，或者满足某种停止准则才停止迭代。

EMD处理sEMG信号方法更加直观、直接、后验以及具有自适应性，EMD分解所用的基来源于原始信号本身。图8表明sEMG信号经过EMD处理后，将信号中存在的不同尺度下的波动或变换趋势逐级分解开，产生了10 个具有不同特征尺度的数据序列，分别为IMF1～IMF10和一个残差Res，并且IMF顺序按频率从高到低排列。IMF相较原始的sEMG信号变得平稳，有利于后续提取相关的特征进行手势识别。

2.2 特征提取

本文先对sEMG 信号进行EMD 分解，使其平稳化，根据与原始信号之间的相关性选择相关系数较大的前几阶IMF 分量进行小波包分解，提取小波包系数能量（En）、平均绝对值（MAV）、最大值（MAX）、均方根值（RMS）和方差（VAR）等特征。

由于分解出的IMF 分量可能会因为过分解产生冗余的成分，因此需要选择出最有效的分量，只是简单的选择其中几阶IMF 提取特征，无法达到较好的识别效果，并且不同手势动作分解出的IMF 与原始信号相关性强弱不一样。本文通过求取所有IMF 分量和原始信号之间的相关系数Cr，将相关系数较大的前几个IMF 分量作为有效分量进行小波包分解，相关系数Cr可以表示为：

其中，Xi为原信号数据点，yi为IMF分量数据点，N为信号长度，xˉ和yˉ分别为Xi和yi相对应的信号平均值。

计算12 种手势下各样本经分解得到的各个IMF分量与各自原始信号相关系数的平均值如图9所示。可以发现sEMG 信号经分解后得到的前4 个IMF 与原始信号之间的相关性较大，表明信号的主要信息包含在前4个IMF分量中，综合考虑算法的复杂性和精确性，本文选取前4个IMF分量。

图9 IMF分量与原始信号的相关系数Fig.9 Correlation coefficient between intrinsic mode function and original signal

小波包变换是小波变换的一种拓展，小波变换可以看作是时频窗自适应短时傅里叶变换，小波变换只分解低频信号，忽略高频信号中的有效信息，小波包是一种更精细的分析工具，可以同时分解低频和高频信号，给定小波双尺度关系：

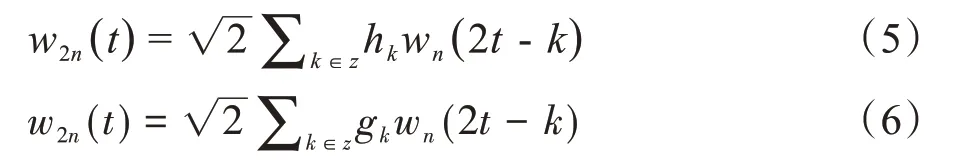
当n=0 时，w0(t)是标度函数；n=1，w1(t)是小波函数，hk和gk分别是高通滤波器和低通滤波器，函数集wn(t)是小波包函数，具有正交性，紧凑性，分析信号能力较强的特点，常用的小波包函数有Db 系列、Haar 小波、Sym 系列和Dmey 小波等，本文分别采用Db3、Dmey、Haar和Sym8小波基函数对每组4通道数据作3 层分解［31］，并从第3 层小波包分解系数中提取相关的特征。

（1）平均能量（En）可以表示信号的强弱，其计算公式如下：

（2）平均绝对值（MAV）是小波包系数绝对值的平均值，很好地说明了sEMG 绝对值的变化趋势，其计算公式如下：

（3）最大值（MAX）反应了动作过程sEMG 幅度的变化范围及剧烈程度，其计算公式如下：

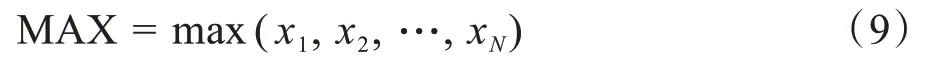
（4）均方根（RMS）信号的均方根可以很好反映出随机信号的幅值特征，计算公式如下：

（5）方差（VAR）表示sEMG 与平均值偏离的程度，计算公式如下：

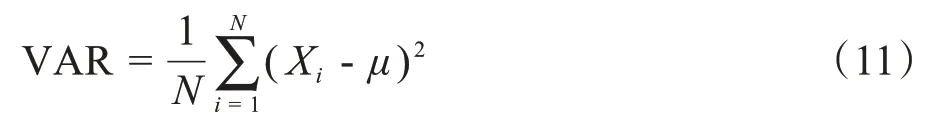
3 LDA和SVM手势分类

LDA 分类器计算简单、易于实现、训练速度快，SVM 有良好的泛化能力和较高的识别准确性，本文选择LDA和SVM作为分类器，进行手势分类研究。

LDA 分类器是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

SVM 分类器是从线性可分情况下的最优分类面提出的一种监督学习模型［32］，被广泛用于模式识别中，SVM 的多分类是在二分类的基础上发展来的，通过核函数将输入样本映射到高维空间，在新的高维空间中求得最优分类面，而这种映射是通过定义合适的内积数来实现的。

4 结果分析

4.1 不同小波函数比较

为了验证提出的EMD-WPT肌电信号手势识别的可行性，对比Db3、Dmey、Haar和Sym8 5种常用的小波函数进行3层小波包变换，并从第3层小波包系数中提取En、MAV、MAX、RMS和VAR 5种特征，采用LDA分类器和SVM分类器时的识别正确率如表1和表2所示。结果表明Db3小波函数下提取特征的效果比其余3种好，故本文选择Db3作为WPT的小波函数。

4.2 LDA与SVM的对比

为了验证识别模型的有效性，分别采用LDA 和SVM 分类器进行手势识别，将EMD-WPT 提取小波包系数进行手势识别分别记为Y-LDA 和Y-SVM；将直接提取小波包系数特征进行手势识别记为N-LDA和N-SVM。Y-LDA 和N-LDA 两种模型识别正确率对比如图10所示，Y-SVM和N-SVM两种模型识别正确率对比如图11所示。

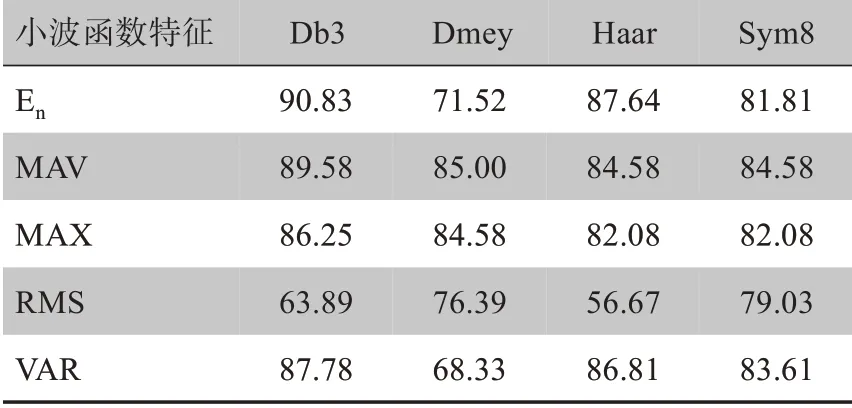
表1 LDA分类器下不同小波函数的识别正确率（%）Tab.1 Recognition accuracy of different wavelet functions in linear discriminant analysis(LDA)classifier(%)

表2 SVM分类器下不同小波函数的识别正确率（%）Tab.2 Recognition accuracy of different wavelet functions in support vector machine(SVM)classifier(%)

图10 LDA分类器下两种模型的对比Fig.10 Comparison of the two models in LDA classifier

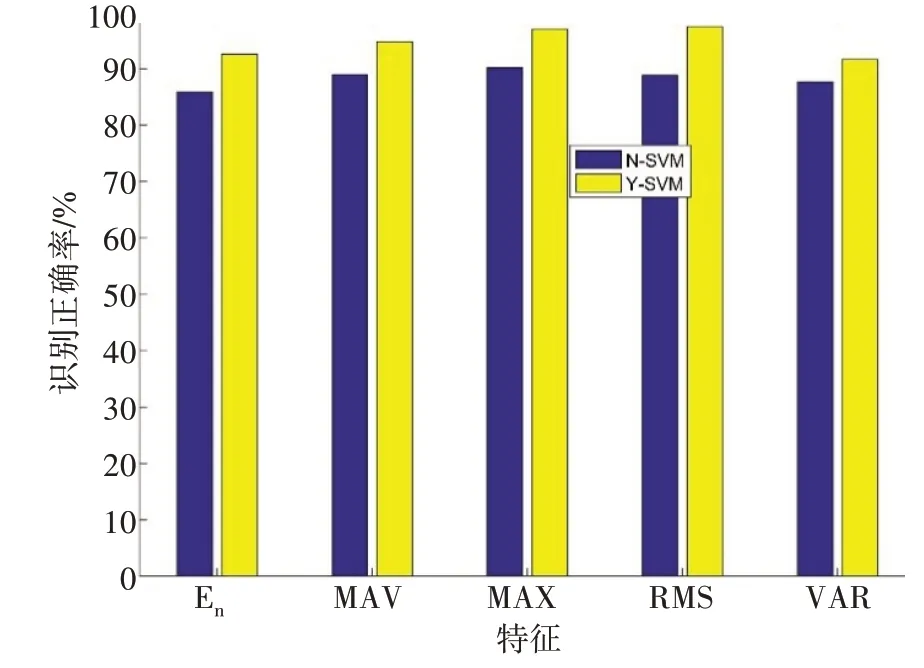
图11 SVM分类器下两种模型的对比Fig.11 Comparison of the two models in SVM classifier

识别正确率不仅取决于所使用的分类算法，还取决于提取到的特征，图10表明，在LDA分类器下，EMDWPT 提取小波包系数作为特征效果比WPT 好，并且EMD-WPT提取小波系数能量的手势动作平均识别正确率最高，真实标签和预测标签混淆矩阵如图12所示，手势3有4个样本被识别为手势4，手势4有11个样本被识别为手势2，手势7有3个样本被识别为手势6，其平均识别正确率为97.50%，而直接提取小波包系数能量特征的手势识别正确率仅为86.25%，平均识别正确率提高了11.25%。图11表明，在SVM分类器下，相比于WPT提取特征，EMD-WPT效果更好，并且EMD-WPT提取小波包系数最大值特征的手势动作识别平均识别正确率最高，真实标签和预测标签混淆矩阵如图13所示，手势3有15个样本被识别为手势4，手势6有1个样本被识别为手势7，手势7有2个样本被识别为手势6，平均识别正确率为97.50%，而直接提取小波包系数最大值特征的手势识别正确率仅为88.83%，平均识别正确率提高了8.67%。

图12 LDA分类器混淆矩阵Fig.12 Confusion matrix of LDA classifier

5 结束语

图13 SVM分类器混淆矩阵Fig.13 Confusion matrix of SVM classifier

本文针对小波包分解sEMG分类效果差，提出了一种有效的肌电信号手势识别模型，通过短时能量将数据分割，然后对分割后的数据进行EMD，并选择与原始信号相关性较强的固有模态函数作为有效分量再提取小波包系数中的相关特征，提高了手势动作的识别正确率，在LDA和SVM分类下，12种手势识别正确率最高达到97.50%，sEMG通过EMD后再提取WPT系数中的特征，有利于提高sEMG手势识别的正确率，但对手势3和手势4的识别仍然有较高的误识别率，以后的研究可以考虑多个特征融合，多个识别方法以及优化算法进行结合，从而达到更理想的结果。