激发学习内驱力 让数学课堂“活”起来
□费建法
(杭州市余杭区五常中学,浙江杭州 311112)
课堂教学要关注学生学习价值观的培养,以提高学生学习的兴趣和质量.学生的学习价值观是指学生对学习目的、意义、作用的认识,它是激发学生学习动机的内驱力.只有在课堂中激发学生学习内驱力,才能让学生进行深层次的学习,才能让数学课堂“活”起来.如何激发学生学习内驱力,是新课程理念下亟待解决的问题.下文笔者结合具体教学实践,从营造课堂氛围、把握知识点、挖掘课程资源三个层面对如何激发学习内驱力展开探讨.
一、营造轻松的课堂环境,让课堂氛围“活”起来
轻松幽默的教学环境对学生学习内驱力的提升至关重要,学生在温馨愉悦的课堂环境中会发挥自己最大的学习潜能,达到最佳的学习状态.教师可以用多样的教学方法去营造轻松幽默的课堂环境.
教师可以利用中学生好胜的心理特点,在教学中开展游戏竞赛,如你问我答、比一比谁算的快又对、小组对抗赛、“找朋友”等.例如,复习《圆的基本性质》这节内容,由于概念、性质定理特别多,如果把所有的性质和判定用幻灯片放一遍,没有新意,学生不爱听,记忆也不深刻。对此,教师可以设置一个小小的游戏:
看图说定理:考考你的眼力,请观察下列5 个图形(图1),你能说出对应的定理吗?比一比哪一组说得快、说得准?
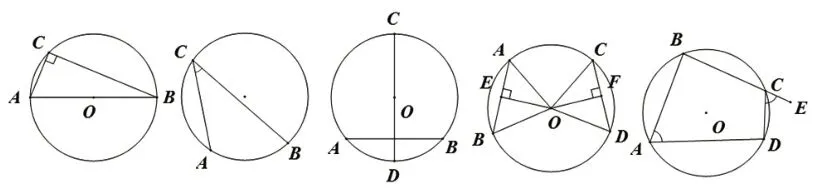
图1
小组竞赛的形式可以为学生创造展示自我、表现自我的机会,提高他们学习数学的兴趣.很难掌握的定理,通过你说我说大家说,每个学生都能认真聆听站起来回答的同学有没有漏条件、有没有说错,以便及时补充,展现自我.这样的设计使一节很枯燥的复习课变得有趣了.它通过营造轻松的课堂环境,让课堂氛围先“活”起来,把学生的注意力迅速引入到课堂学习中.
二、精准把握知识起点,让数学认知“活”起来
把握知识起点就是要了解学生的学情,教师要把重心放在学生知识疑点和知识的增量上,这样才会促使学生打开思维,激发学习内驱力.在新课引入阶段,教师可以通过开门见山的提问或者少量练习两种方式来判断学生的知识起点在哪里.
比如,在学习平行四边形边、角性质的时候,可以提问学生:“你已经知道平行四边形的哪些知识?请说一说.”
很多学生都会说出平行四边形的对边平行且相等、对角相等、不稳定性等,但是对平行四边形对角线互相平分这个知识点不是很清楚,还有对平行四边形边、角、对角线三个维度的学习方法不理解.此时,教师可以追问:“你是怎么证明这些结论的?请你动手试试.”
通过这样的诊断性提问,教师可以快速知晓哪些知识学生已经掌握,哪些知识还有疑点和盲点.教师抓住这些疑点和盲点展开教学,学生就会“顺藤摸瓜”去学习新知,这样课堂就更接“地气”.
另外,教师可以通过少量练习诊断学生当下的学情.比如,我们在教分式方程新课的时候,可以设计如下诊断材料:
(3)给下列方程分分类,并说明你分类的理由.
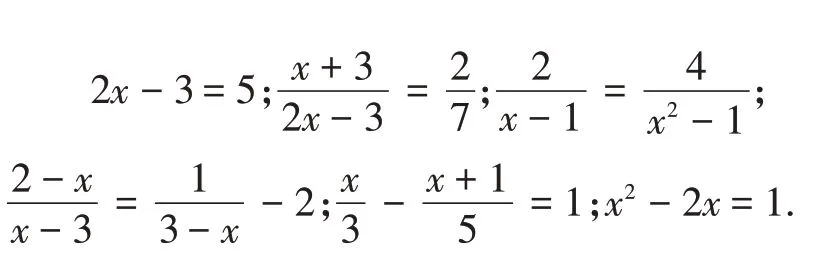
教师通过练一练(1)(2)两道习题可以快速诊断出学生对分式有无意义和最简公分母知识的掌握情况,这对新课解分式方程有铺垫作用.练一练(3)要求学生根据已有的一元一次方程经验对方程进行分类,为分式方程的概念教学埋下伏笔.
教师只有精准把握学生的学情,建立知识间的整体联系,然后根据学生知识的疑点、盲点之处展开教学,才能真正激发学生学习的内驱力,让学生的数学知识“活”起来.
三、充分挖掘课程资源,让学生思维“活”起来
(一)引用数学史料
在教学中渗入数学史文化,利用数学史文化巧设问题情境,可以使学生在学习数学的过程中通过数学史文化感受数学问题的精妙有趣,从而激发学习欲望,提升学习内驱力.比如,在《探索勾股定理》新课引入环节,我们可以设计如下问题情境:
相传两千多年前,古希腊著名的哲学家、数学家毕达哥拉斯去朋友家做客.在宴席上,其他的宾客都在尽情欢乐,只有毕达哥拉斯却看着朋友家的方砖地发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他,谁知,毕达哥拉斯突然恍然大悟的样子,站起来,大笑着跑回家去了.原来,他发现了地砖上的三个正方形存在某种数学关系.
教师可以顺势引出课题:“在这种数学关系中隐藏着一个历史上伟大的定理,就是勾股定理,今天我们就一起来学习《探索勾股定理》.”这样就一下子将学生吸引到数学的问题中来,进而增加他们思维的广阔性.
(二)巧用数学工具
用好工具也能够激发学生的求知欲望,启发学生的思维.比如在学习等腰三角形“三线合一”的时候,教师可以开门见山设计悬念问题:
将一把三角尺和一个重锤,如图2 放置,就能检查一根横梁是否水平.你知道里面蕴含什么数学知识?

图2
教师适时创设“悬念”,将会使学习成为学生不断追求、探索知识的心理需求.
(三)多用生活经验
数学源于生活又应用于生活,很多数学的问题都可以在生活中找到原型.教师可以将学生的生活中的例子引入数学问题,比如在学习两点间线段最短时,可以创设这样的生活经验:
从你家A到学校B有 5 条路,如图 3 你会选择走哪一条?说说你的理由.

图3
又如在在学习多边形密铺的时候,教师可以利用学生家里装修的生活经验,让学生自己设计铺设的方案:
如图4,如果瓷砖都是正三角形,那可以密铺吗?为什么?如果是正方形、正五边形、正六边形呢?哪些图形可以密铺,哪些不可以?为什么?

图4
教师还可以拓展到任意四边形、五边形、组合图形……
创设良好的问题情境可以激活学生的求知欲,促使学生为问题的解决形成一个合适的思维意向,可以把原来枯燥的数学课堂变得有趣生动,让学生思维“活”起来,从而收到最佳的教学效果.教师可以通过不同的问题情境教学,调动学生学习热情和积极性,提升其学习数学的内驱力,增强其思维的流畅性.
(四)善用问题链接
美国教育家杜威提出:“教学的艺术就是向学生提问,指导学生探究并养成其独立探索的习惯.”在学生的心灵深处,都有一种强烈的探究需求,其关键在于教师会不会发问.教师可以设计探究式问题串激发学生的求知欲,引发学生对数学问题深度思考.例如,在学习《探索勾股定理》时,可以从毕达哥拉斯的地砖中提取一大两小三个正方形图形如图5、图6.

图5
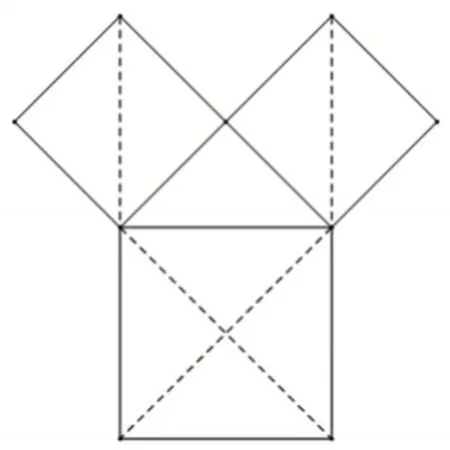
图6
教师可以这样设置问题串:
问题1:大正方形的面积和两个小正方形面积之间有什么关系?
追问1:正方形的面积和RT△的边长有什么关系?
追问2:上述图形中两个小正方形的面积是相等的,RT△中的两条直角边是否相等?接下去你会如何思考这个问题?
追问3:当RT△三边不等的时候,a=3,b=4,c=5,如何验证勾股定理?如图7.
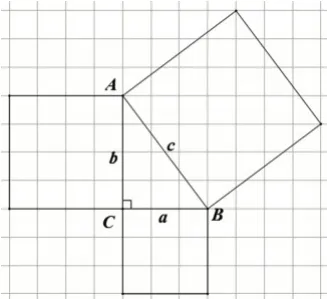
图7
追问4:如果RT△三条边不是整数,我们用什么办法去验证勾股定理?
对于问题1,学生用割补法就能很自然地发现大正方形的面积等于两个小正方形的面积.但从正方形面积之间的关系到RT△三边关系还有个探究的过程,不能马上得出勾股定理.追问1引导学生发现正方形面积等于边长的平方,把原来面积之间的关系转化到边长的数量关系,从而验证勾股定理.追问2 可以引导学生思考:如果两个小正方形面积不等,也就是RT△ABC中两条直角边不相等,如图8,勾股定理a2+b2=c2还成立吗?可以利用什么方法证明?对于追问3,学生仍可以通过数格子找到面积之间的关系来验证勾股定理.同时学生还发现可以利用外弦图(如图9)来计算大正方形的面积.追问4,教师可以这样引导学生对勾股定理探究做出深度思考:把特殊的整数边拓展到一般情况,该如何思考?同时,教师可以渗透从特殊到一般的数学思想方法.这时,教师可以借助几何画板,让学生上台进行验证,观察直角边长在不断变化,什么关系没有改变,学生通过直观就能发现a2+b2=c2.
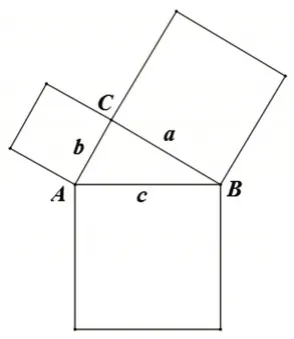
图8
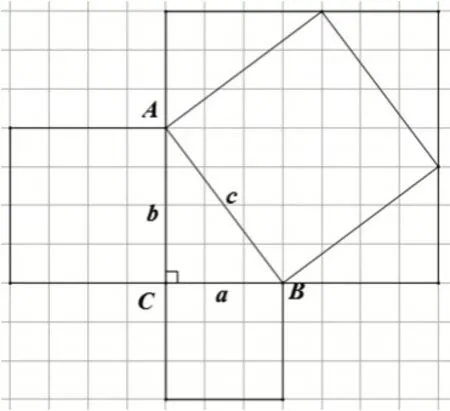
图9
“问题”是数学的心脏,是激发学生学习的原动力,教学过程中可以按照“从定性到定量”“从特殊到一般”的研究路径来设置问题串.教学应把学生熟悉的特殊图形作为学习的起点,层层设问,引导学生发现和提出一般性的结论,再通过演绎推理来证明结论的正确性.同时,“问为什么”是学生的天性,教学应提高学生发现和提出问题的能力,而不是抹杀学生天性.教师应引导学生去发现和提出想研究的内容,这是一件非常有意义的事情.
总之,在数学课堂中,教师可以从营造轻松的课堂环境、精准把握知识起点、充分挖掘课程资源三个方面去激发学生的学习内驱力.在教学中,教师应引导学生主动参与学习,在获得基本知识和基本技能的同时,经历知识的发生和发展过程,从中明白知识是如何产生的、知识是如何运用的,从中积累数学学习的基本经验,感悟数学的基本思想.这样的数学课堂,不仅能让课堂氛围“活”起来,而且能让知识“活”起来,更能让学生深层次的数学思维“活”起来 .

