圆锥曲线动弦过定点问题“同构”求解的思维策略

□周如俊

（灌南中等专业学校，江苏灌南 222500）

例题（2020 年全国卷Ⅰ理科第20 题）已知A，B分别为椭圆的左、右顶点，G为E上顶点为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D.

（1）求E的方程；

（2）证明：直线CD过定点.

第（1）问易求，椭圆E的方程为本文着重对第（2）问进行“同构”思维探究.

一、“同构”运算思维的“过渡桥”

“同构”运算思维的“过渡桥”，主要是指探寻圆锥曲线动弦过定点问题的条件与结论之间的问题同构、逻辑重组、等价化归，追究解法的自然与具有普遍指导意义的通性、通法，从而提炼一类问题解决的基本思想.

数学运算“同构”是解决高考问题、获得数学结果不可缺失的学习环节.对于直线CD过定点问题，自然的思路是把直线CD方程化为y-y0=k(x-x0)的形式，则定点为(x0,y0).其解法因坐标设点而异，选择不同运算方向、不同运算方法，解题过程繁简不一，但是曲径通幽.

方法一：直求法 .设P点坐标(6,m)，通过直线PA、PD与椭圆两个交点特征，由韦达定理分别求出两点坐标，写出直线方程CD，即从而完成定点证明.此法解法自然，但对学生运算素养要求较高.

阿峰给我们推荐了一家当地特色的餐馆，就在老市场那边，那条街有许多酒吧餐厅还有卖当地物品和一些旅游纪念品的商店。那家餐馆生意很好，等着吃饭的人在街边排队。阿峰说回去的时候你只要叫辆突突，两块钱就可以把你们送回酒店。这里通用美金。阿峰觉得我们除了看古迹也应该去逛逛这条街，因为这是暹粒现在最繁华和热闹的地方了。

方法二：特值法.从特殊情况同构，如点P(6,6)，易求出直线CD方程为猜想定点坐标结论，再论证猜想，体现解题思维的严谨性.此法结论明确，但论证中求解坐标计算运算量偏大，仍是考生此法越不过的“算”坎.

方法四：斜率法.利用椭圆上点与任意关于原点对称的两条连线的斜率乘积为定值的常 用 结 论故有-3yy=(x-3)(x-3（)以下解法

CDCD同代换法），从而避免非对称式中因无法使用韦达定理解题被“卡住”的尴尬局面，体现了“对称转化”的同构简化策略.

方法六：齐次法.依据“大道至简”、“移中不变”（斜率值不变）原理实施齐次化变换，利用过原点两条张弦斜率之积为定值的简洁特性，快速求出直线mx'+ny'=1 中m，n之间关系，从而锁定定点坐标，有效降低运算的难度.

具体解法是：

此外，还有仿射法[1]，即“伸缩变换”（化“椭”为“圆”）、“简化运算”的“同构”思维策略，有关文献已阐述，不再赘述.

二、“同构”解法思维的“中转站”

“同构”解法思维的“中转站”主要是指探寻圆锥曲线动弦过定点问题的条件与结论之间的异题同解、解法归一、模式同构，追寻解法的“化归”与“改头换面”形异质同的试题的识别、破解，从而抓住一类问题解决的本质思想.

借鉴齐次法解法，通过数学抽象与数学建模，可将例题化归为“常态二次圆锥曲线（圆、椭圆、双曲线、抛物线）F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2≠ 0)上给定的P点与异于P点的动弦MN两端点之间斜率之和（之积）为定值时，求解（证）动弦过定点的问题”，借助数学语言表征出相关“通法”引理与定理，能凸显解题的数学本质.

首先给出如下引理（证明过程略）.

【引理】M、N常态二次圆锥曲线F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2≠ 0) 上 异于给点P(x0,y0)的动弦MN两端点.已知直线PM，PN的斜率存在，分别记为kPM，kPN.将原点平移到点P(x0,y0)，设平移后的直线M'N'方程为mx'+ny'=1 ，并 记F1=2Ax0+C，F2=则有：

利用引理，给出如下定理（证明过程略，有兴趣的读者可参阅笔者拙文[2]）.

【定理】常态二次圆锥曲线F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2≠ 0)上有一定点P(x0,y0)与异于P点的动弦MN两端点. 已知直线PM，PN的斜率存在，分别记为kPM，kPN.并记F1=2Ax0+C，F2=2By0+D.

1.若kPM+kPN=λ，则有：

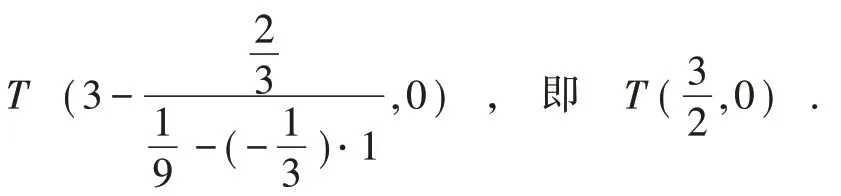
上述定理“同构”常态二次圆锥曲线动弦过定点（定向）问题，形成一类简捷、易记、便用的通法，克服了相关结论推导过程繁杂、表达式形式不一、相互间关联度低、识记难等缺陷.

依托高考试题数据分析，是探索与“同构”数学本质、关联和规律的重要研究手段，有利于增强学生基于数据表达现实问题的意识.文献大数据分析表明，2018 年全国卷（理）Ⅰ第19 题、2017 年全国卷（理）Ⅰ第 20 题、2016 年浙江高中竞赛第17 题、2013 年江西卷（理）第20 题、2011 年全国高中联赛第 11 题、2010 年江苏卷第18 题、2009 年辽宁卷（理）第22 题、2005 年江西卷（理）第20 题、2004 年北京卷（理）第17题等高考（竞赛）试题都属于圆锥曲线动弦过定点类问题.

三、“同构”命题思维的“背景源”

“同构”命题思维的“背景源”主要是指探寻圆锥曲线动弦过定点问题的条件与结论之间的异题同源、命题同质、解答同法，探寻解法的“共源”与“命题盖头”的揭秘、规律的破译，从而领悟一类问题解决的核心思想.

极点与极线是高考圆锥曲线有关直线过定点的试题命题的隐含的一种背景知识.“一点一线一世界”，通过数学抽象与数据分析“同构”，可以“识破”试题中蕴含的有关极点与极线的知识背景，并将使高考试题解法建构为高度概括、表达准确、结论一般、有序多级的思维系统，从而有效把握命题的规律．

借助范方兵、王芝平的研究[3]所得，笔者给出如下极点与极线的主要性质：

【极点和极线的几何定义】如图1，P不是圆锥曲线上的点，过P点引两条割线依次交圆锥曲线于点E，F，G，H，连接EG，FH交于点M，连接EH，FG交于点N，则MN为点P对应的极线，直线MP为点N对应的极线，直线PN为点M对应的极线，MNP称为“自极三点形”.

图1

【极点和极线的代数定义】已知圆锥曲线Γ为Ax2+Cy2+Dx+Ey+F=0 ，则 称 点P(x0,y0) 和直线=0 为圆锥曲线Γ的一对极点和极线.

【极点和极线的调和共轭】如图2，设极点P关于圆锥曲线Γ的极线为l，过极点P任作一割线交Γ于A，B，交极线l于Q，则反之，若有则称点P，Q调和分割线段AB，或称点P与Q关于调和共轭．

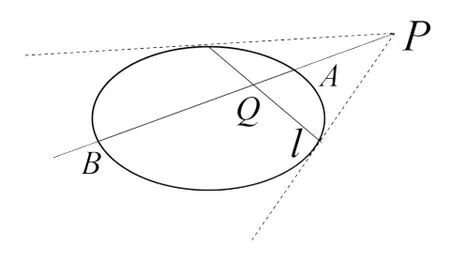
图2

以极点极线作为背景命制的试题屡见不鲜［如2019 年全国Ⅲ卷（理）第21 题、2008 年安徽卷（理）第22 题、2011 年四川卷（理）第21题等］，这既是高考考查潜能的需要，也是命题者学术背景使然[4].圆锥曲线的极点极线性质，与“普法”思维联合与“同构”，既能“秒杀”试题的答案，也能增加试题解答的“珠联璧合”.

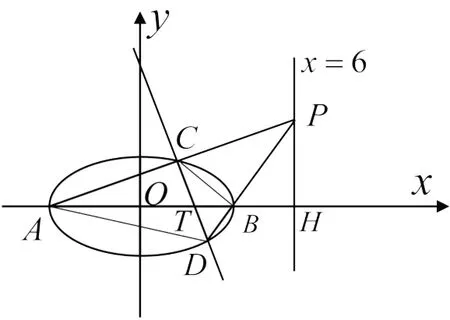
图3

对于例题溯源，第（2）问：如图3，极点P(6,m)的极线+my=1 过定点同样，极点的极线为x=6.运用极点极线知识求解可瞬间锁定答案.