基于正交仿真试验的柔性网开网参数评估方法

卞伟伟，邱旭阳，刘 亮，贾彦翔

(北京机械设备研究所，北京 100854)

0 引言

柔性网作为一种有效的捕获“低慢小”无人机目标的方式[1-3]，其空中展开过程作用时间短、动态变化快，流固耦合现象严重，且相比于空间飞网，其处于超低空，气动环境复杂多变，地面试验尚难以模拟其动态特性，导致柔性网展开过程存在很大的不确定性[4]。柔性网最大开网面积、滞空时间、有效拦截面积是考核柔性开网性能优劣的核心指标，直接关系到柔性网拦截弹度、牵引头质量、弹射速度、弹道倾角等参数直对目标的拦截与压制效果；而弹体速度、弹射角接决定了上述核心指标的实现。

确定影响柔性网开网过程的灵敏度参数，不仅可以大大减小后期参数采集和数据整编的工作量，还可以在装备论证设计的过程中，对照战技指标快速调整模型的输入参数，提高仿真效率，也可以为柔性网拦截弹的优化设计提供参考和借鉴，但想要精确获得以上参数信息相当困难。文献[5]对导弹的气动灵敏度进行分析；文献[6-7]在飞行器优化设计的参数分析上做出了一些有益的探索，但是目前鲜有关于柔性网战技指标的灵敏度研究，所以有待进一步挖掘和探索。

灵敏度分析最常用的方法是直接求导法。这种方法思路清晰，容易理解，但只能应用于变量少、能写出系统数学表达式的系统，而柔性网的各类战技指标，比如最大开网面积、滞空时间、有效拦截面积等，与柔性网拦截弹在低空开网过程的弹体速度、弹射角度、牵引头质量、弹射速度、弹道倾角等主要物理参数之间往往无法写出相对应的表达式，更无法直接求导，只能根据开网结果输出得到两者之间大致的关系。文献[8-10]提出的基于正交实验的灵敏度分析，对于离散、不可微或隐式的系统灵敏度分析十分有效，目前得到了广泛的应用。

因此，为尽可能覆盖较大的参数范围，减少仿真计算工作量，科学评估各个影响因素对开网指标的影响，本文基于正交试验法[11-12]对仿真工况进行设计，在应用极差法对影响因素进行重要性排序的基础上，采用方差法对影响因素的显著程度进行判断，实现了对正交试验结果的各项性能指标进行参数灵敏度分析与主次梳理，为柔性网拦截弹其他战技指标的灵敏度分析提供参考。

1 灵敏度分析方法

正交试验结果的灵敏度分析方法包括极差法和方差法。

1.1 极差法

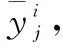
(1)

式中，pj为第j因素所划分水平的数目。

Rj越大则说明该因素对该指标的影响越大，该因素越重要，据此可将各因素按照重要性进行排序。极差法的优点在于简单直观，计算量少，但是它无法估计试验误差的大小，也无法提出一个标准来判断因素的作用是否显著。

1.2 方差法

方差法的基本思想是将指标的总离差分解成因素的水平变化引起的离差和误差引起的离差两部分，然后构造F统计量，作F检验，从而判断因素的显著程度。设因素j的水平变化引起某指标的离差为：

(2)

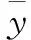
误差引起的离差也有与式(2)相同的形式。构造F统计量如下：

(3)

式中，fj、fe分别为因素j和误差e的自由度。

Fj越大说明该因素对该指标的影响越大，该因素越重要，也可据此进行重要性排序。若Fi>F1-α(fi,fe)，则认为因素j对该指标有显著影响，否则无显著影响，其中，α为置信水平。由此可见，方差法相对于极差法的一大优势在于可以判断因素的显著程度。

2 正交仿真试验设计

2.1 参数选取

以六边形柔性网为例，网型构型如图1所示。六边形网由放射形网线组成，可分为网格绳、边线绳、牵引绳和连接绳，绳网对角顶点的长度为10.6 m，名义最大展开面积为72.98 m2。

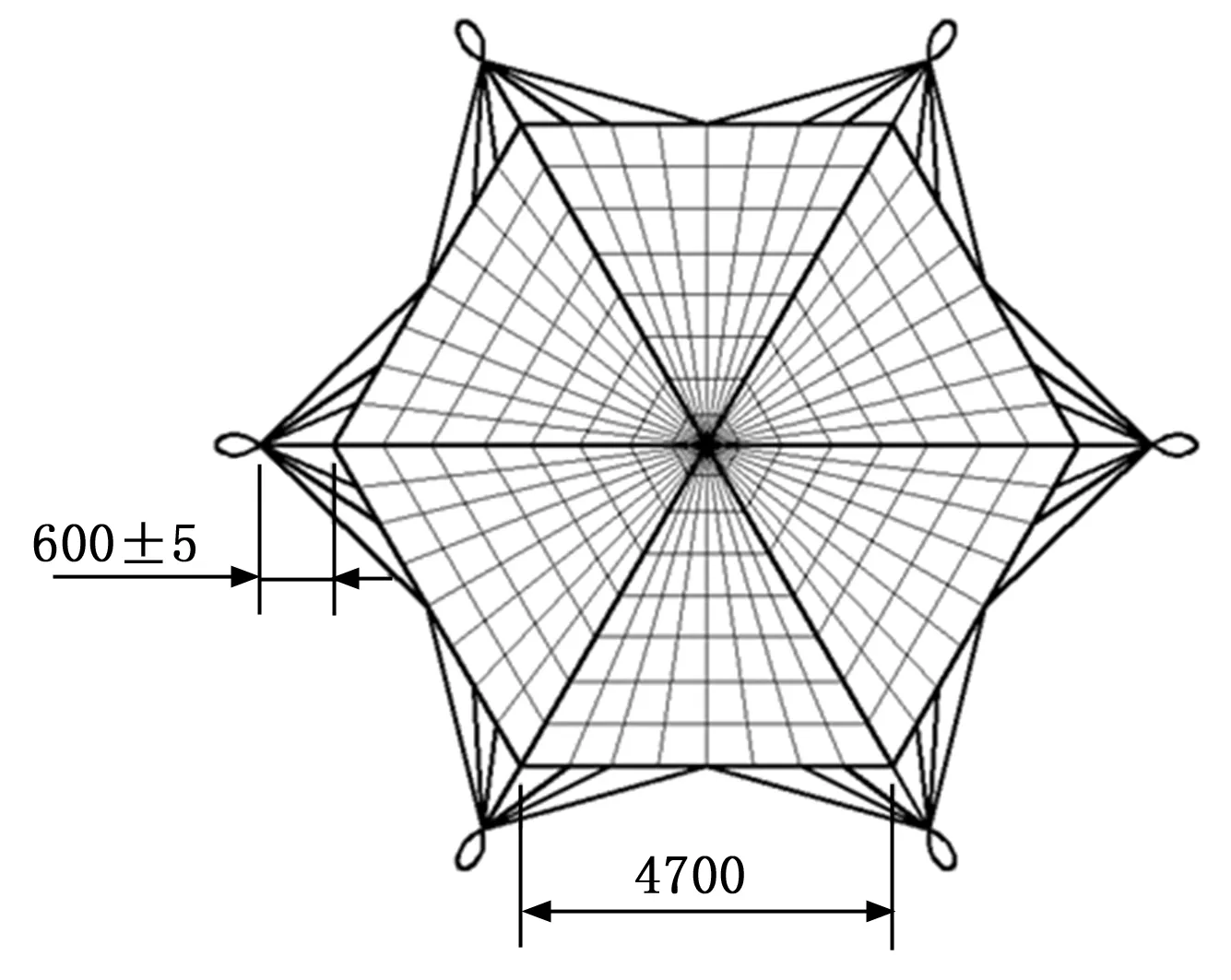
图1 六边形绳网构型

影响柔性网开网性能指标的主要变量包括：柔性网拦截弹初始弹道倾角、弹体速度、牵引头质量、牵引头相对拦截弹的弹射角度和弹射速度。上述各个量的物理含义如图2所示。

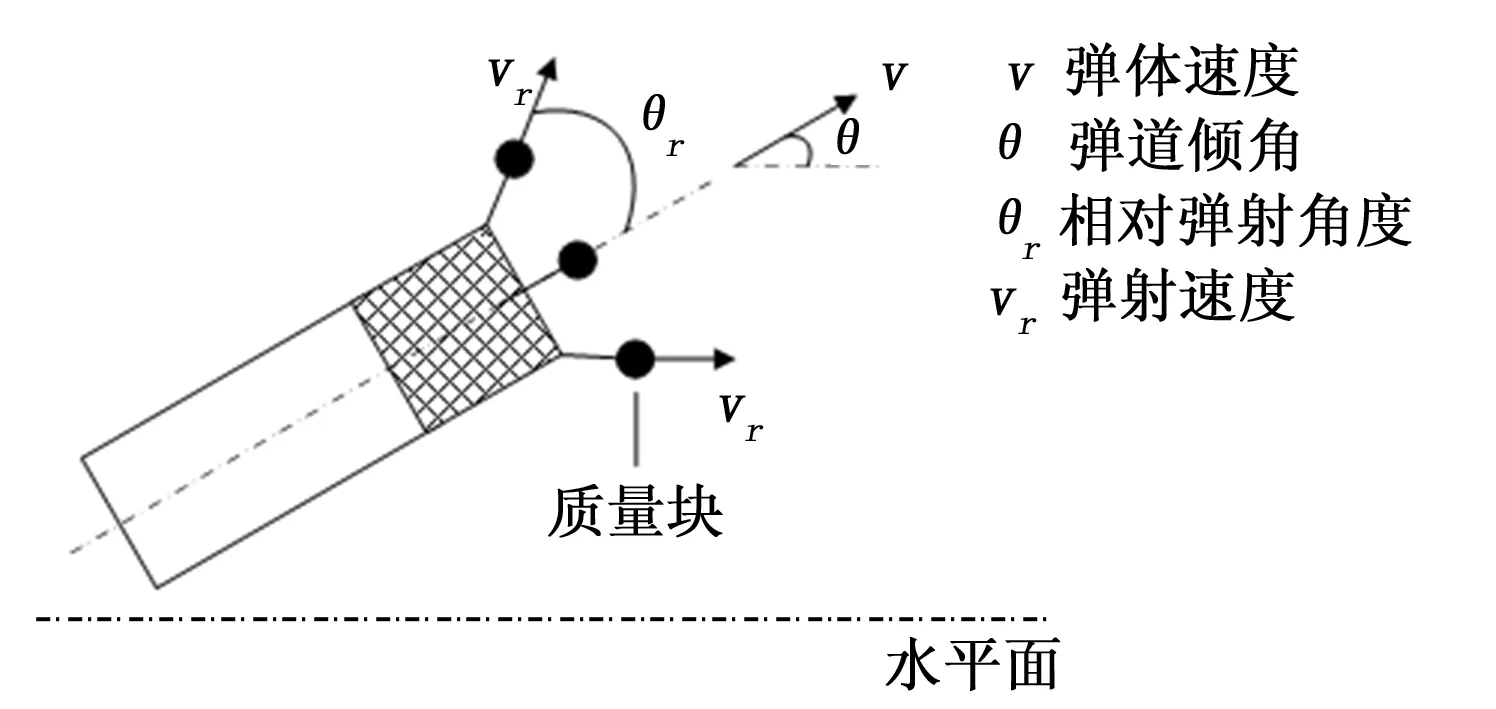
图2 柔性网开网参数说明图

2.2 正交表构造

正交表是指导正交试验设计的重要表格[8]，其记法为Ln(ji)，其中，L是正交表的符号，n表示正交表的行数(试验次数)，j表示正交表中的数码(因素的水平数)，i表示正交表的列数(试验因素的个数)。

本文采用的正交表为L25(56)，由于只选取了5个因素，因素正交表中有一列为空。每个因素的水平划分如表1所示，其中θ为弹道倾角、v为弹体速度、m为牵引头质量、θr为质量块弹射角度、vr为质量块弹射速度。正交试验表如表2所示，从表中可以看出表中任意一列各水平均出现且出现次数相等；任意两列之间各种不同水平的组合均有可能出现，且出现次数相等，体现了正交设计表“均匀分散、齐整可比”的特点。

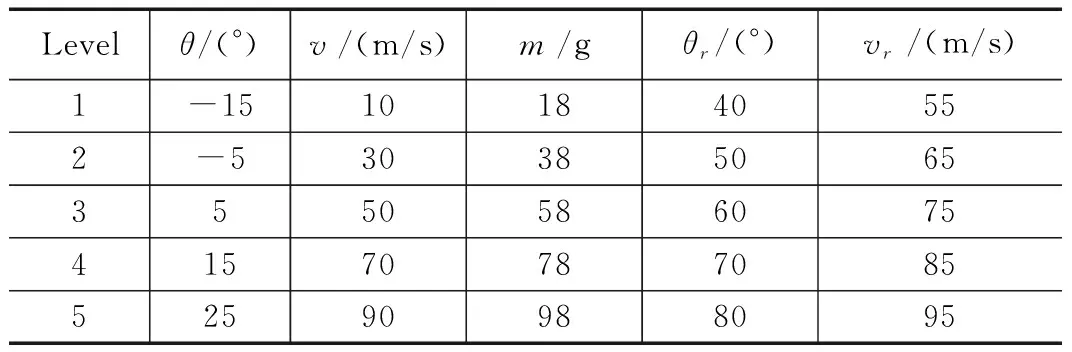
表1 六边形网正交试验设计的因素与水平

3 灵敏度参数分析

3.1 最大开网面积灵敏性分析

最大展开面积正交仿真试验得到的最大展开面积如表3所示，弹道倾角θ等5项参数在不同水平下对试验结果的影响，计算结果如表4～8所示，由式(1)可得到弹道倾角对应的极差为Rθ=7.57的计算结果如表9所示。

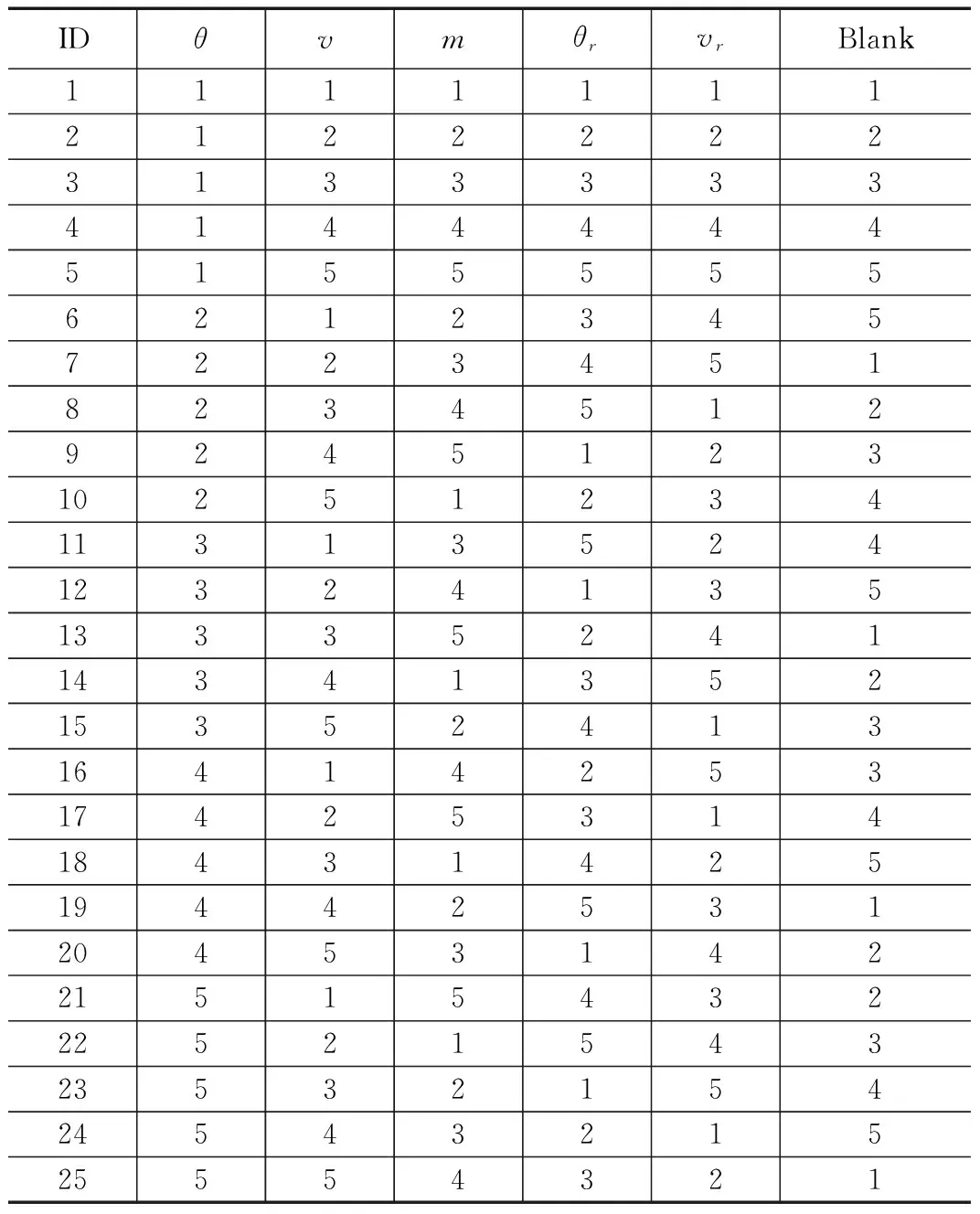
表2 正交仿真试验设置表

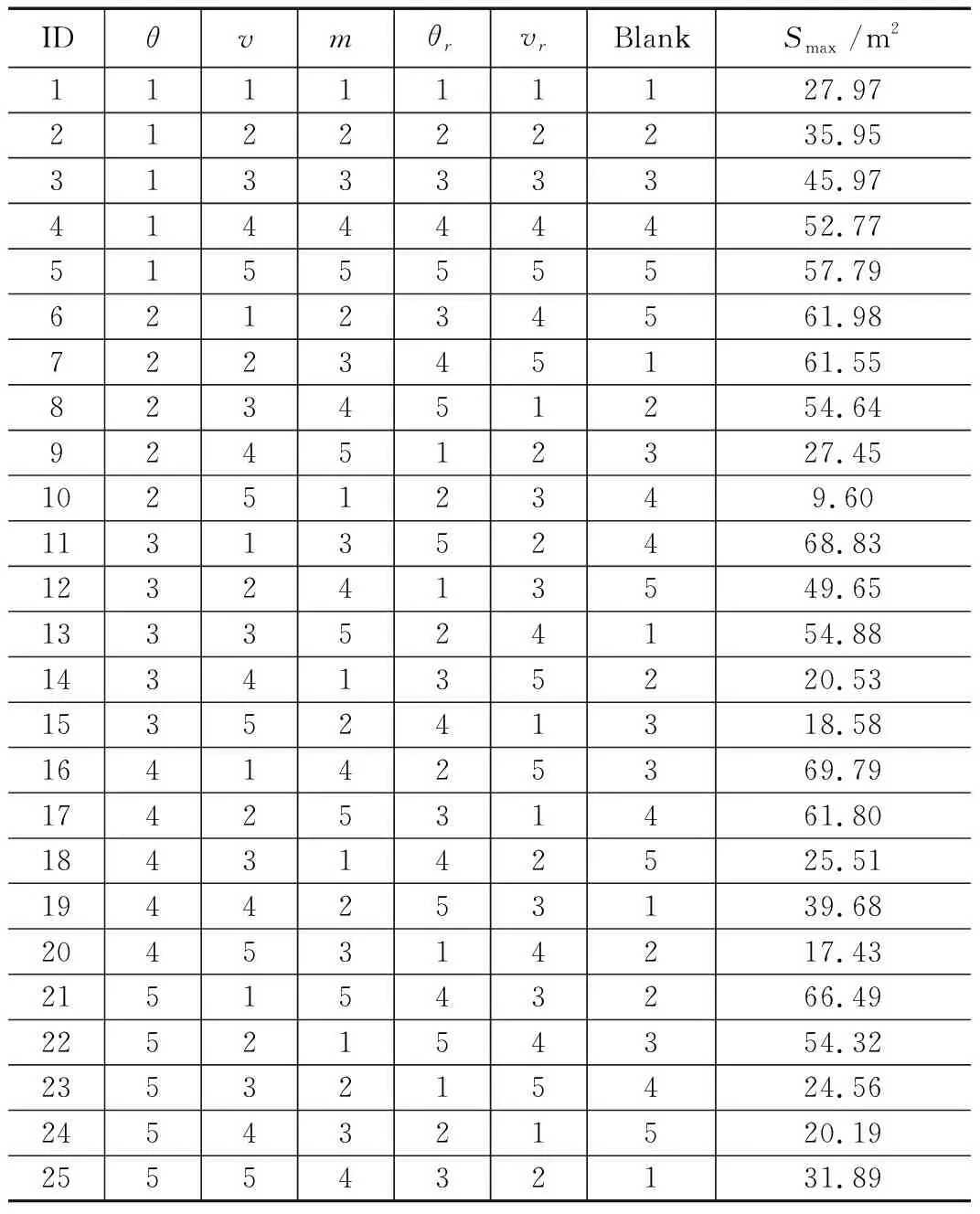
表3 正交试验中的最大开网面积

表4 弹道倾角不同水平下的最大开网面积

表5 弹体速度不同水平下的最大开网面积

表6 牵引头质量不同水平下的最大开网面积

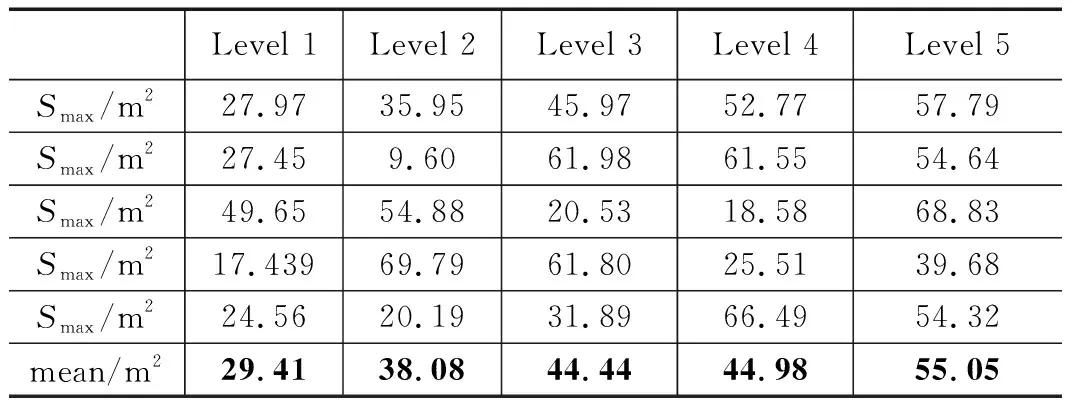
表7 弹射角度不同水平下的最大开网面积

表8 弹射速度不同水平下的最大开网面积

表9 不同因素的极差

从表中可以看出，对最大展开面积影响最大的因素的弹射速度，其次是牵引头质量、弹射角度、弹体速度、弹道倾角。但是考虑到取值范围的不同，将计算得到的极差除以因素的取值区间得到了一组新的数据，以此来考察因素变化单位值时最大展开面积的极差，分别得到在弹道倾角每变化一度时最大面积的极差变化为0.19 m2；弹体速度每变化1 m/s时，最大面积变化为0.12 m2；质量块质量每变化1 g时，最大面积变化为0.26 m2；弹射角度每变化1°时，最大面积变化为0.42 m2；弹射速度每变化1 m/s时，最大面积变化为0.88 m2。综合平均意义下的极差和正交试验极差，对最大展开面积影响较大的是质量块弹射角度和弹射速度。

按照极差做出不同因素对最大展开面积影响的饼图如图3所示。从图中可以看出网体的发射参数是影响柔性网展开最大面积的主导因素，而弹体的运动参数是影响柔性网展开面积的次要因素。从物理规律考虑，这个现象的主要原因是：弹体的弹道倾角和弹体速度影响的是柔性网展开过程中重力相对绳网发射方向的分量以及柔性网在展开过程受到的气动力，这两项力的作用效果远不及增加柔性网初始发射能量对柔性网展开面积的影响，增加柔性网发射在展开方向的能量包括增加弹射速度、弹射角度及牵引头质量，即影响柔性网展开面积的三项主要因素。在正交试验选择的仿真参数设置范围内，这三项因素所占的权重为83%。

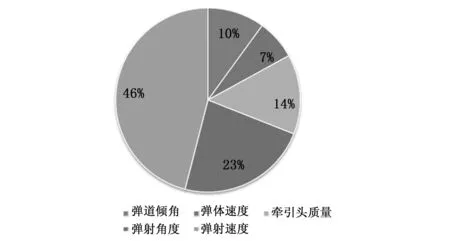
图3 不同因素对最大展开面积影响权重饼图

方差法的作用在于可以判断因素影响的显著程度。利用式(2)和表3中的数据，分别计算得到各个因素的平均值和离差，如表10所示。各个因素的F统计量可由式(3)计算得到，取置信度为0.95，因素和误差的自由度均为4，可得到影响显著性阀值为F0.05(4,4)=6.39。

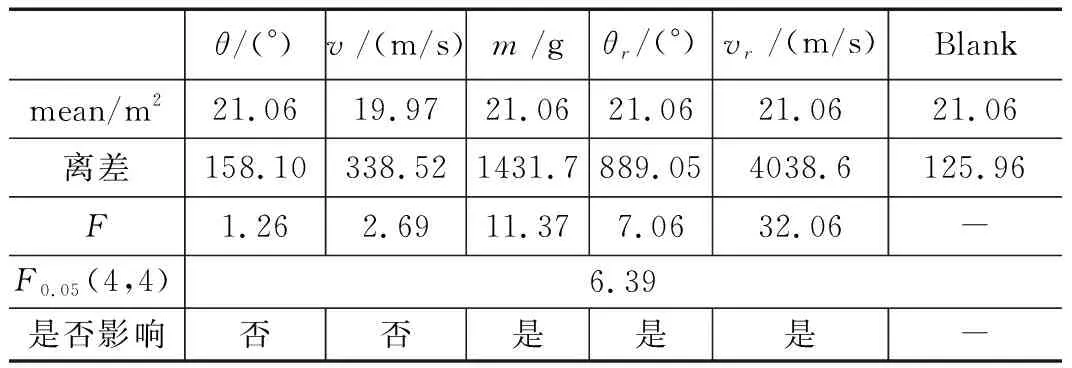
表10 各因素的方差分析

从各因素的方差分析结果来看，对最大展开面积影响最大的因素依次为：弹射速度、牵引头质量、弹射角度、网弹速度、弹道倾角。图4为各因素在不同水平下的平均最大展开面积，可以看出对弹道倾角、弹体速度这两个不具有明显作用的因素来说，平均最大展开面积与因素水平间不存在明显的线性化关系，而对于牵引头质量、弹射速度、弹射角度这3个具有明显作用的因素来说，最大展开面积与因素水平间具有明显的线性化关系。

图4 平均最大展开面积随因素水平变化图

3.2 滞空时间参数灵敏性分析

六边形网滞空时间的正交试验结果如表11所示，各个因素在不同水平下的滞空时间如表12～16所示，极差计算结果如表17所示。从计算结果来看，各个因素对滞空时间影响的大小从大到小依次为：弹射速度、弹射角度、牵引头质量、弹体速度、弹道倾角。从图5可以看出，滞空时间与牵引头质量、弹射速度、弹射角度均呈负相关关系，等效地，滞空时间与柔性网在展开方向的能量呈负相关关系。按照极差大小，绘制了各个因素的影响权重如图6所示，可以看出，弹道倾角和弹体速度对于滞空时间的影响较小。

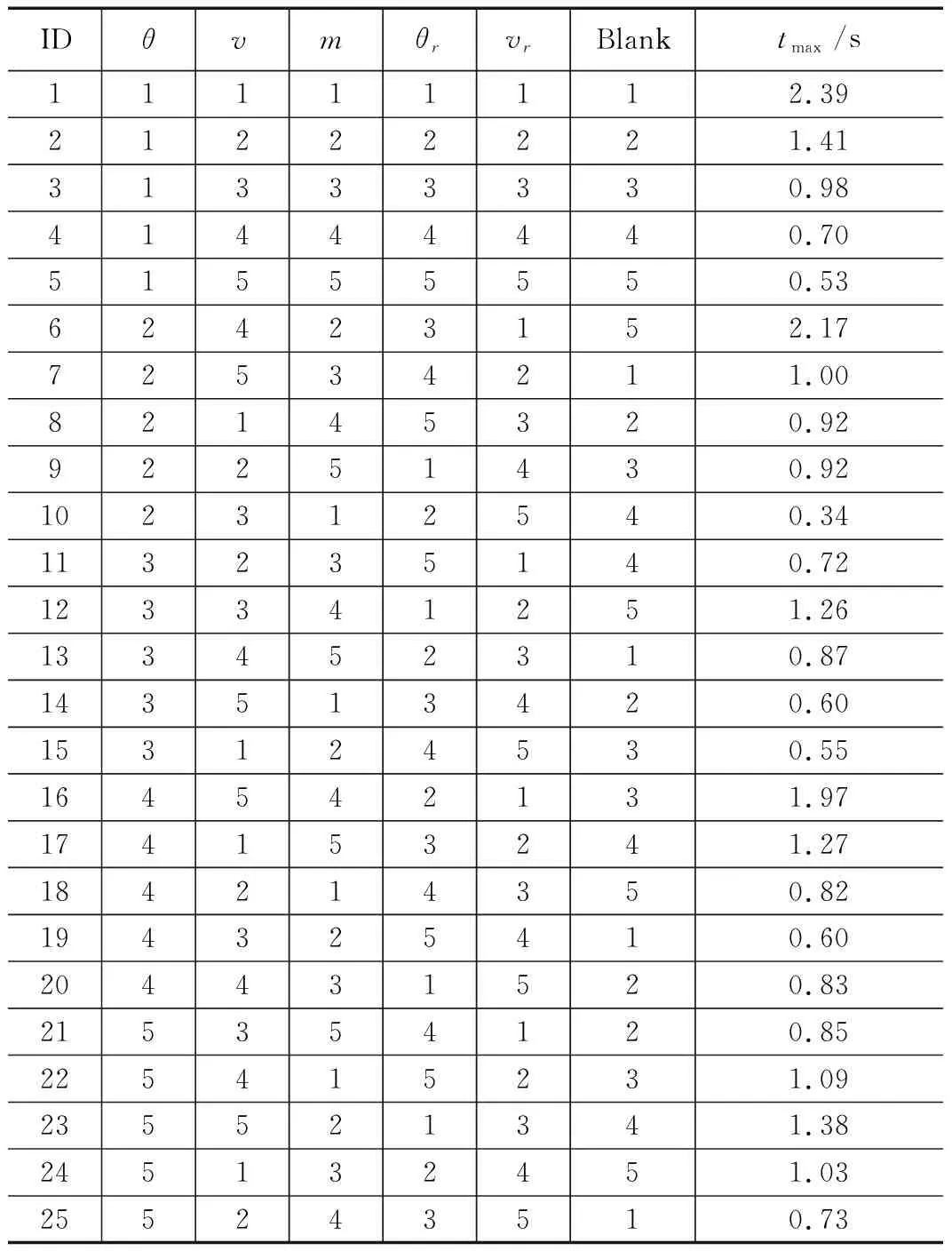
表11 正交试验中的滞空时间

表12 弹道倾角不同水平下的最大开网面积

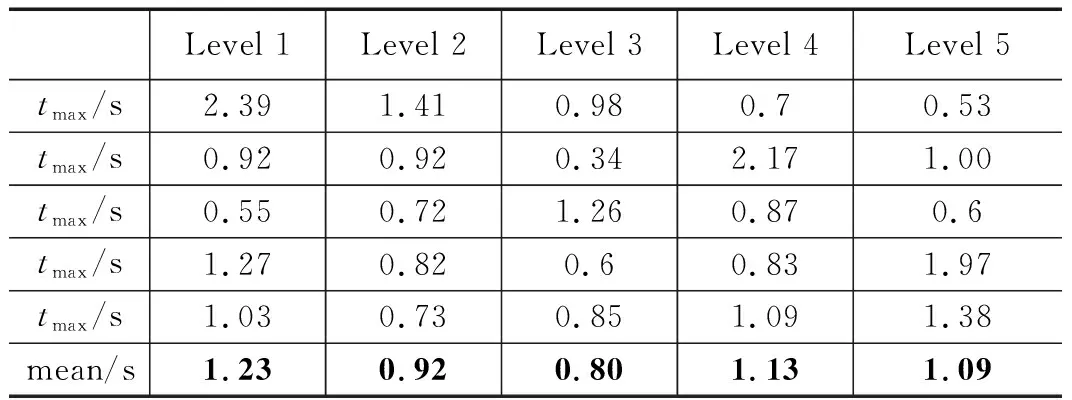
表13 弹体速度不同水平下的最大开网面积

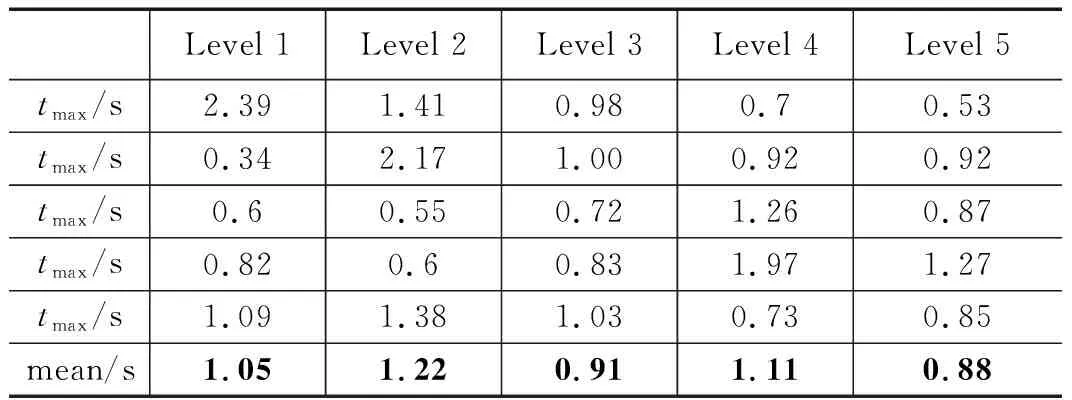
表14 牵引头质量不同水平下的最大开网面积

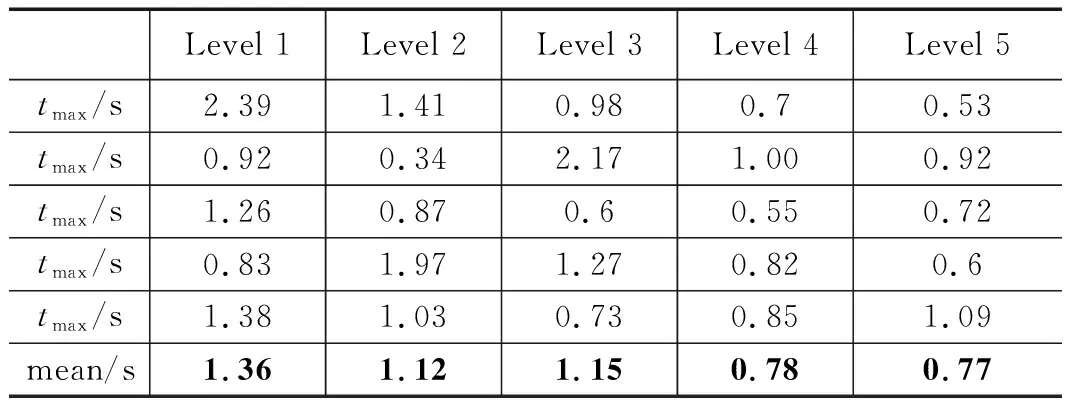
表15 弹射角度不同水平下的最大开网面积

表16 弹射速度不同水平下的最大开网面积

表17 不同因素的极差

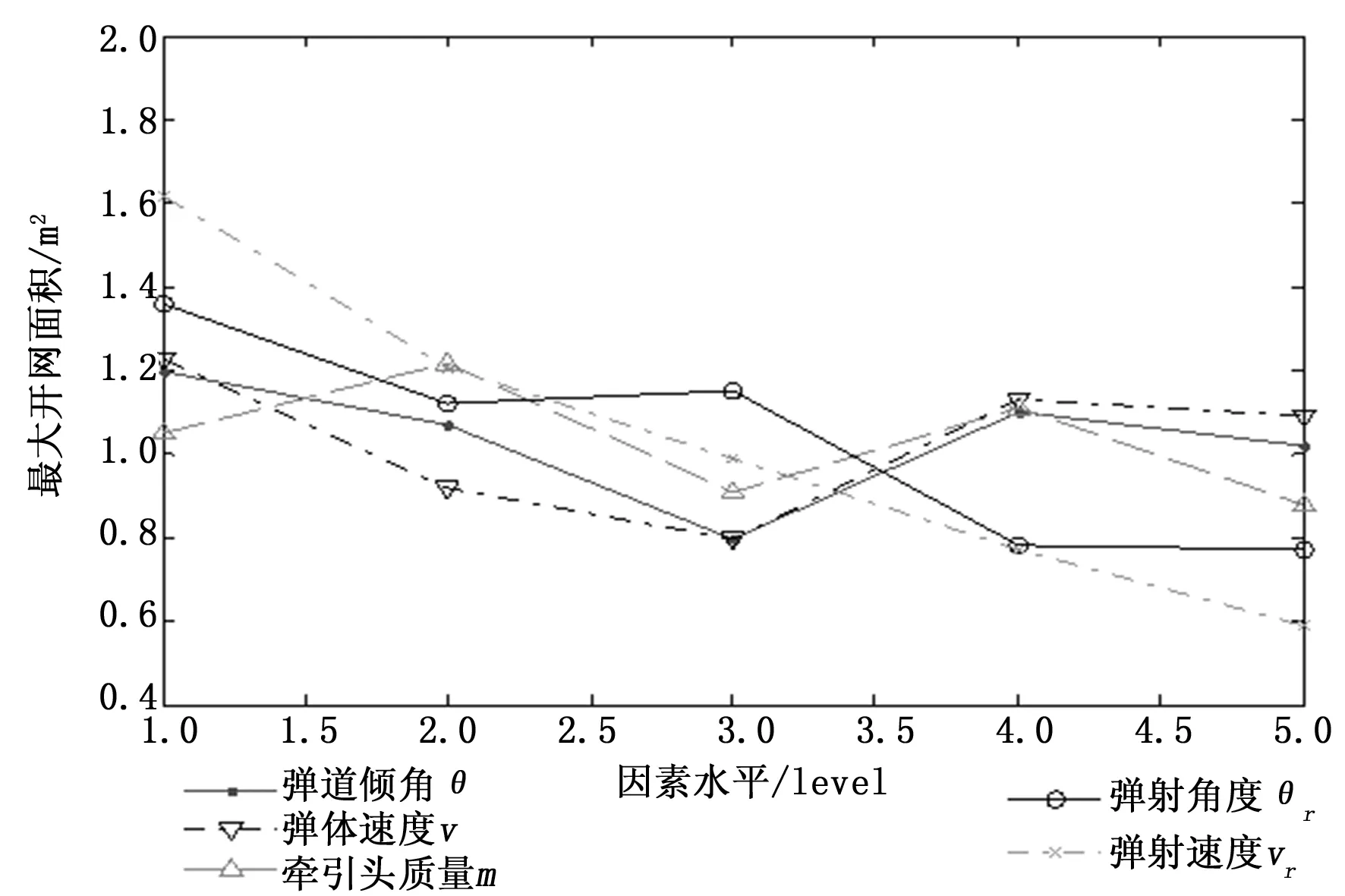
图5 滞空时间随因素水平的变化图

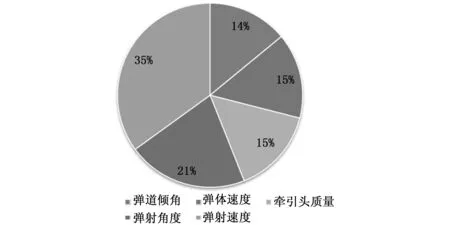
图6 六边形网不同因素滞空时间极差饼图

表18为六边形网的方差分析结果，各个因素的影响权重规律与极差分析结果一致，在95%的置信度下构造F统计量仅有弹射速度对滞空时间是存在影响的。

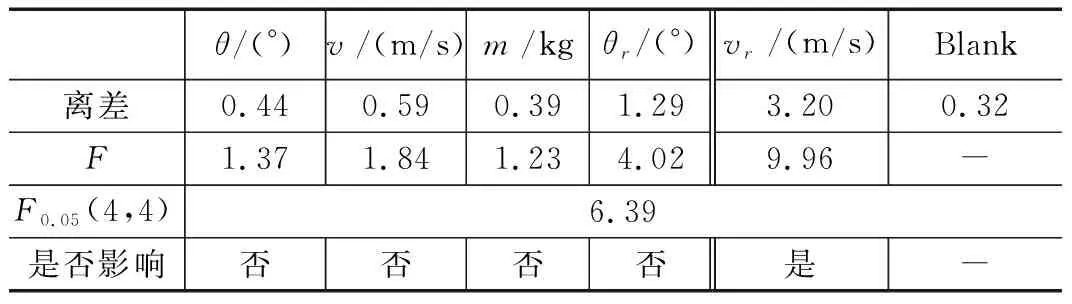
表18 各因素的方差分析

3.3 有效拦截面积灵敏性分析

六边形网有效拦截面积指的是网的展开面积在铅垂面内的投影，它是评估柔性网对水平飞行目标捕获能力的一项重要指标。六边形网有效拦截面积的正交试验结果如表19所示，各个因素在不同水平下的有效拦截面积如表20～24所示，正交试验的极差分析结果如表25所示。与六边形网的最大展开面积对比分析可以看出，除了弹道倾角因素对应的极差数值变化较大外，其他因素的极差基本和六边形网最大展开面积的极差相近，体现了弹道倾角对于有效拦截面积的影响，由于正交试验中弹道倾角的数值选取较小，因此弹道倾角对应的极差数值较小。各个因素对有效拦截面积的影响权重与最大开网面积基本一致。表为各个因素水平变化时，有效拦截面积的变化趋势图，从图7中结果来看弹体速度与有效拦截面积呈负相关，弹道倾角与有效拦截面积无明显单调性，牵引头质量、弹射角度及弹射速度与有效拦截面积呈正相关。

表19 正交试验中的滞空时间

表20 弹道倾角不同水平下的最大开网面积

表21 弹体速度不同水平下的最大开网面积

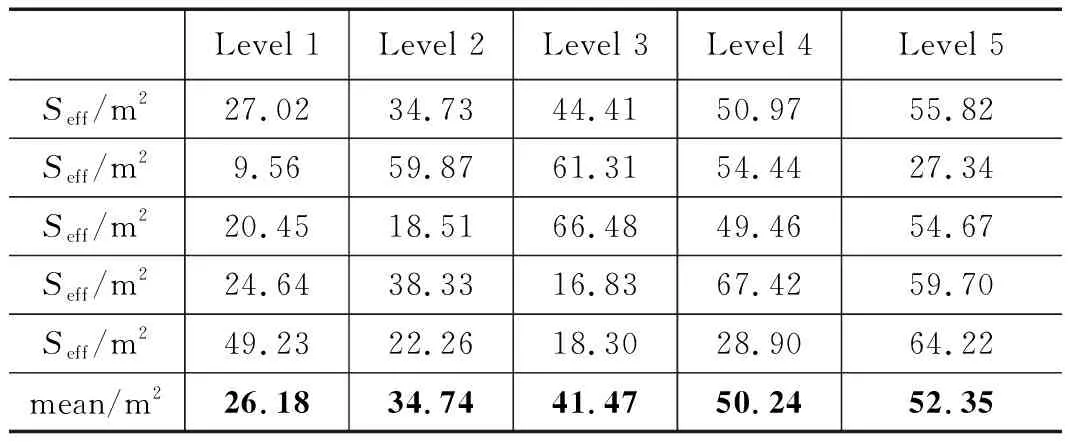
表22 牵引头质量不同水平下的最大开网面积

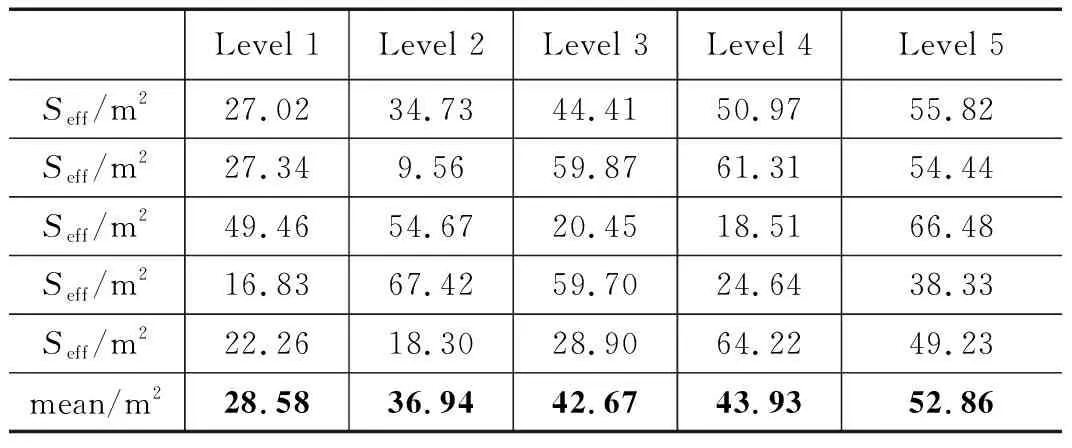
表23 弹射角度不同水平下的最大开网面积

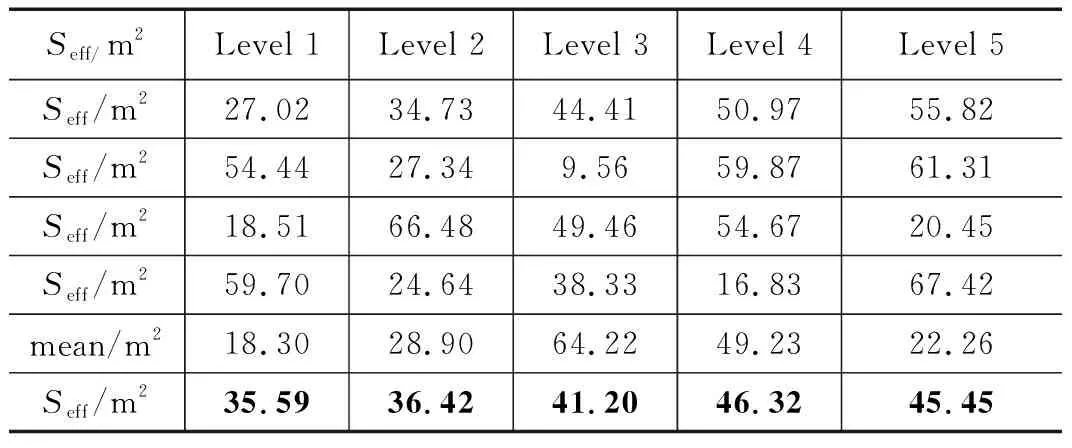
表24 弹射速度不同水平下的最大开网面积

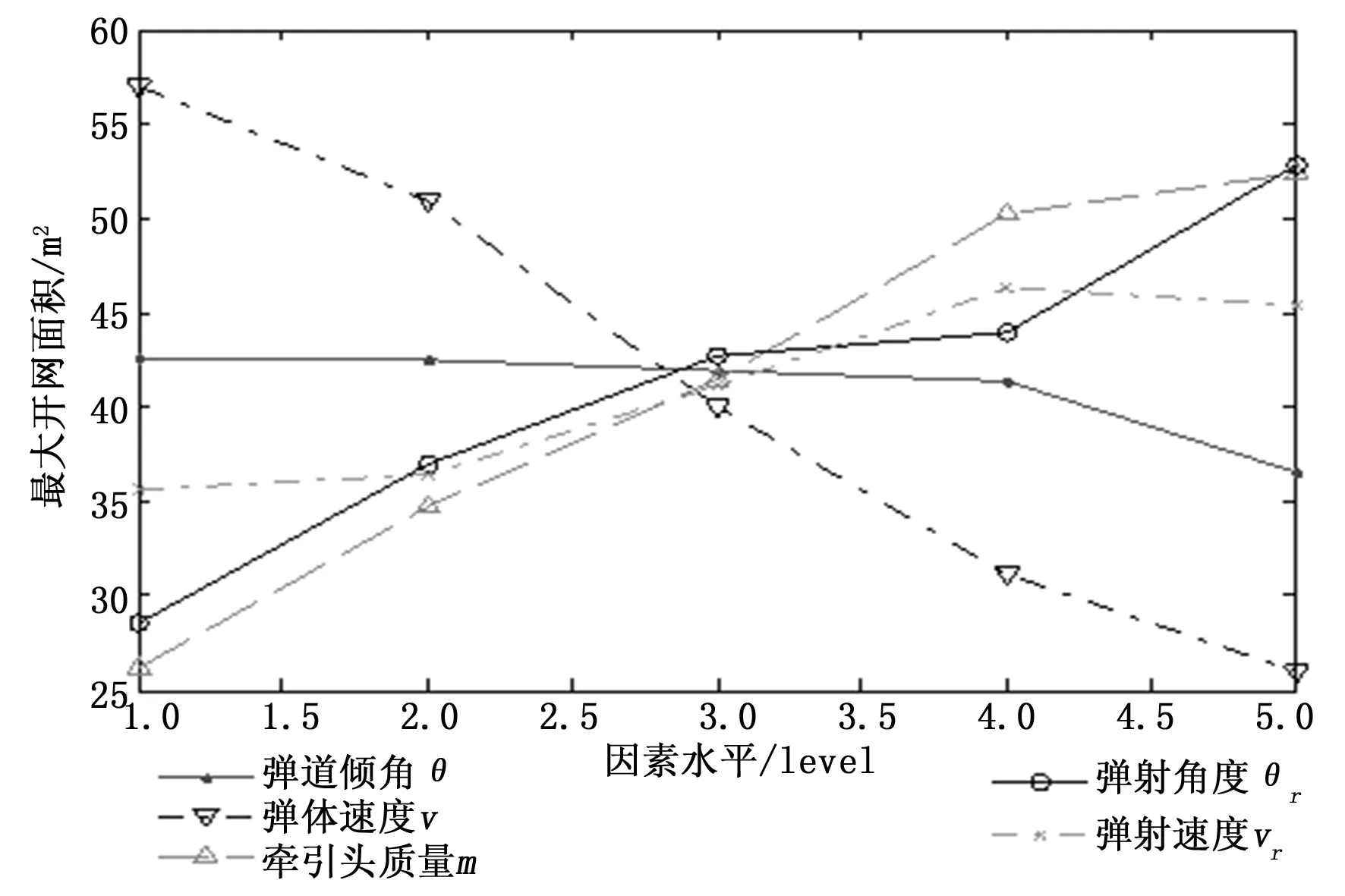
图7 六边形网有效拦截面积随各因素水平变化图

表25 不同因素的极差

六边形网有效拦截面积的方差分析如表26所示，从分析结果来看，弹道倾角对于六边形网的影响较小，一方面这与六边形网特殊的拓扑构型所形成的气动外形有关，另一方面与正交仿真试验中弹道倾角选取的范围较小有关。

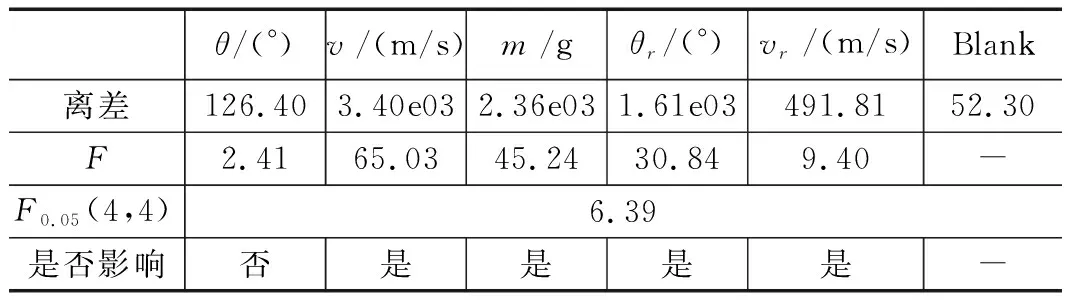
表26 各因素的方差分析

4 结束语

通过正交仿真试验结果分析可形成以下结论：

1)柔性网初始发射动量在展开平面内的投影是决定柔性网滞空时间和最大展开面积的关键物理量。牵引头动量在展开平面内投影的动量越大则柔性网最大展开面积越大，然而，柔性网的滞空时间却越小。因此柔性网的最大展开面积和滞空时间是一对相互矛盾的量，在设计时不可能让二者同时达到最大值，需要根据实际情况，多次利用仿真软件进行计算并结合试验结果寻求最为合理的发射参数组合。

2)从仿真计算中可以看出，弹体速度对于柔性网的最大展开面积和有效拦截面积均有较大的影响，弹体速度越大则最大展开面积有效拦截面积越大。柔性网发射前的弹体速度是经过减速伞减速得到的，因此只要增加减速伞的面积或者作用时间来降低柔性网发射前的弹体速度，则可以很大程度上增加柔性网的最大展开面积，与此同时，由于弹体速度不影响牵引头质量在展开平面内的投影，因此降低弹体速度对滞空时间的影响微乎其微。

本文运用基于正交实验的灵敏度分析方法，对影响柔性网开网效果的相关参数进行了灵敏度分析。根据仿真试验结果，确定了影响柔性网开往性能的主要参数，定性地得出了核心指标与各参数之间的单调性关系。说明该方法在原理上是可行的，可为柔性网开网参数的工程设计提供一定的参考。