基于AFSMC算法的飞机飞行姿态自适应滑模控制系统

魏婉婷，周 勇

(1.延安大学 物理与电子信息学院，陕西 延安 716000；2.河北大学 信息技术中心，河北 保定 071000)

0 引言

近年来，我国飞机飞行姿态控制技术随着微电路控制技术、传感控制技术、数字网络控制技术等诸多相关技术的发展，取得了一系列突破性进展[1]。飞机飞行姿态自适应控制系统是保证飞机飞行姿态保持正确的重要控制系统，飞机飞行姿态控制系统的应用，将电路控制、数据控制、指令分析、数据监测集于一身，飞机飞行姿态控制系统具有控制界面简单，控制数据覆盖面广，控制响应性好等特点[2]。

飞机飞行姿态控制系统在技术层面上存在三大壁垒：姿态控制精度、姿态控制响应与姿态控制稳定，综合对三大壁垒进行分析后，可将其归结于滑模控制问题。针对上述问题，相关领域学者提出了一系列改善方案。文献[3]提出基于高阶微分滑模面的不确定飞机控制系统自适应滑模控制，对飞机姿态控制系统进行坐标变换，并考虑到输入不确定性的存在，基于具有表面和神经网络逼近能力的高阶微分滑模，设计了一种光滑的自适应滑模控制器。该方法控制效果较好，但运行稳定性较差。文献[4]提出基于干扰补偿机制的智能自适应控制策略.设计了耦合多变量干扰观测器作为控制器补偿闭环系统，结合快速超螺旋滑模控制算法和自适应动态规划策略，提出了一种新型鲁棒自适应控制器。该方法运行较稳定，但控制精度较差。

针对滑模控制的多变性、非线性[5]与强耦合[6-8]的特性，提出基于AFSMC算法的飞机飞行姿态自适应滑模控制系统。通过PID控制技术配合AFSMC算法，对系统硬件进行自适应变量结构的优化设计，以控制器的形式对飞行姿态控制信号进行非线性处理，配合AFSMC算法驱动适配，再加以自适应量的模糊策略，提升控制精度，稳定控制效果，降低控制误差，解决飞机飞行滑模控制存在的问题，获得理想的控制效果。

1 飞机飞行姿态自适应滑模控制系统整体架构

飞机飞行姿态自适应滑模控制系统包括硬件模块设计及软件流程设计两部分。控制系统整体架构如图1所示。

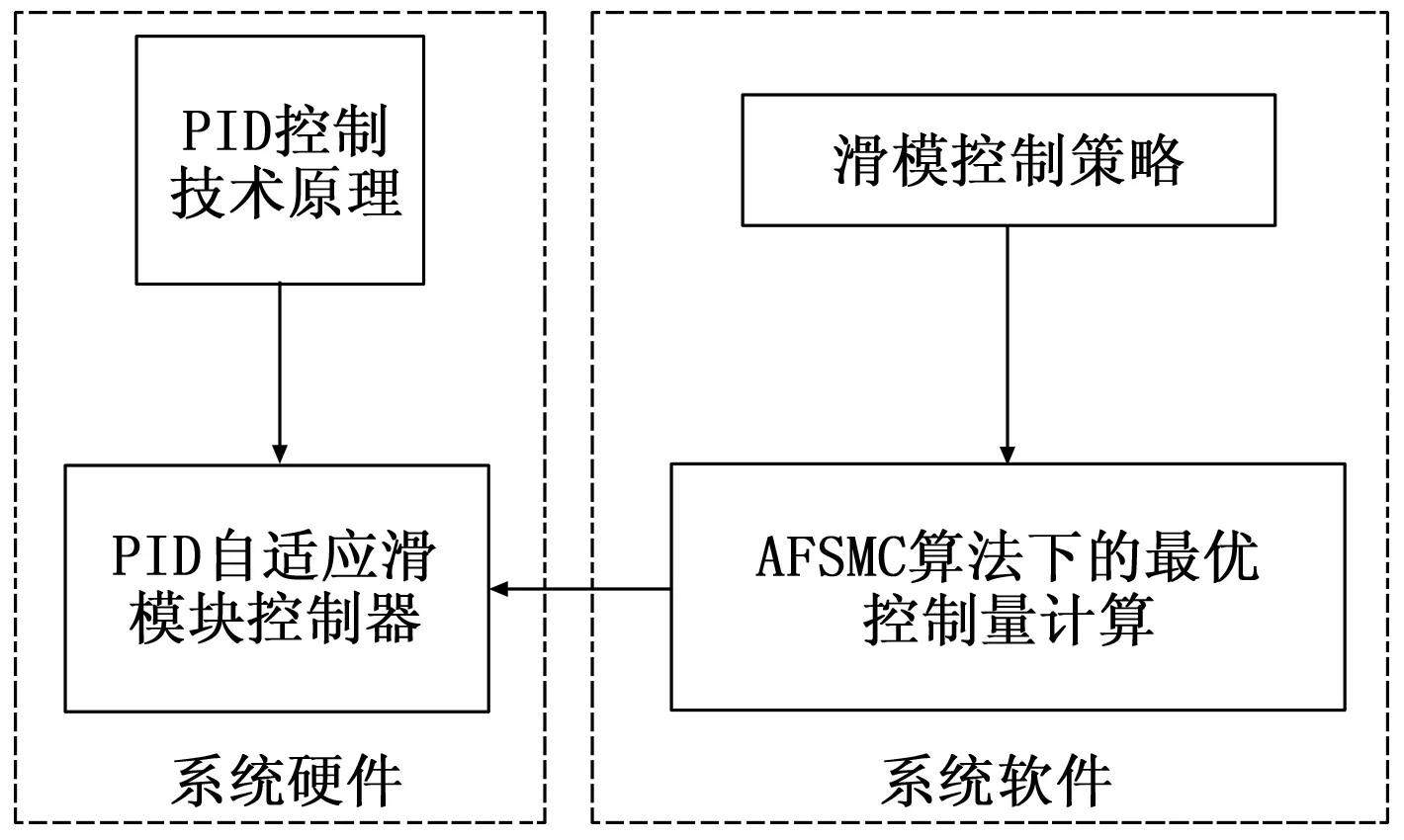
图1 控制系统整体架构

如图1所示，控制系统硬件部分通过PID控制技术原理设计了PID自适应滑模控制器，软件部分通过滑模控制策略提升设计系统对多种场景飞行姿态的精准控制，应用AFSMC算法求得最优控制量，并传输至PID自适应滑模控制器，实现飞机飞行姿态自适应滑模控制。

2 控制系统的硬件设计

2.1 PID控制技术原理

PID 控制技术是众多控制技术中，通过对变量参数的比例关系、积分结构与微分作用计算，完成对线性关系调节控制的一种方法。在实际的应用场景中，普遍应用于线性控制器与非线性控制器的设计中。通过对対作用量输出比例的控制，采用积分控制量[9]与微分控制量[10]对控制变量中的响应系数与调制系数进行拟态差分控制，减小抑制数据造成的误差，提升控制精准与响应速度。通过对控制量下的各项参量的测量与分析，得到较为精准的修正方案，基于此原理，实现PID控制器的设计与调试。PID控制技术原理如图2所示。

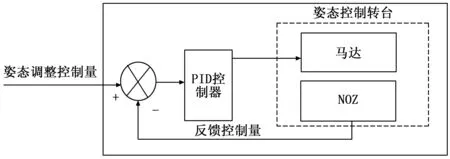
图2 PID控制技术原理图

图2中，基于PID控制技术的控制器载入数据为飞机飞行姿态调整控制量，即飞机在飞行过程中，根据飞行高度与机身仰角状态，作出的调整机身仰角的控制指令数据。其中，飞机飞行过程中机身仰角数据来源于分布在飞机各部分的传感器测量结果。翻开控制量为飞机飞行姿态测量数据与当前飞机姿态仰角数据间的误差所对应的角速度。上述参量对应到硬件系统中，分别对应姿态控制转台的X、Y、Z三轴。X轴为实际飞机飞行姿态的角速度；Y轴为飞机姿态控制滚转误差；Z轴为姿态偏航误差。PID控制技术就是对X轴飞行姿态角对应Y轴姿态控制滚转误差与Z轴姿态偏航误差进行参量一致化的控制。

2.2 PID自适应滑模控制器设计

基于PID控制技术设计控制系统的控制器，同时为了适应设计系统软件部分AFSMC算法，采用飞机飞行空气动力学与飞行运动学模型数据作为控制器设计基础参量，将控制器数据采集端口设计为4项数据采集模式，可同时对飞行姿态传感器4路信号进行采集；同时为了保证控制信号及时稳定输出，控制器输出端设计为六项输出模式，可将控制信号分为6路同步输出。针对传统控制器在对变量、非线性驱动下的强耦合表现，控制器设计在PID控制技术的基础上，对控制电路的非线性变量与耦合量进行了模糊控制量的优化，修正后的控制器电路能够在滑模控制状态中，实现自适应的效果，配合软件部分的算法，能够更好地应对多场景下的姿态控制。设计控制器电路结构，如图3所示。

图3 PID控制器电路结构设计图

图3中，设计为了保证电路对控制信号的稳定，将电路设计为内外两个闭环形态，通过对两个闭环电路[11]的串级控制[12]，实现内环姿态控制信号与外环控制信号间的耦合，消除电路欠驱动状态给控制量削弱。

3 控制系统的软件设计

3.1 自适应滑模控制策略

对控制系统的软件控制策略进行定义，定义利用自适应控制算法的特性，对设计硬件进行软件驱动策略的适配，通过适配自适应策略，提升设计系统对多种场景飞行姿态的精准控制。具体策略定义步骤如下：

1)将控制器输出的滑模控制函数与控制信号跟踪量进行误差测量，得到准确的控制器数据参量；

2)将控制器数据参量定义为S，其对应值设定为0；

3)控制器测量到外界扰动信号时，且扰动量对控制量的影响已超出设定量时，控制器将控制信号对应数值拉回初始值，使其与正常控制信号层面平行；

4)将此状态下的控制仰角设定为0；

5)引入非线性函数运算机制，对控制信号、控制角度、跟踪误差三组参量进行积分计算；

6)根据积分计算结果，创建理想控制环境；

7)在理想环境下对控制量的特征进行规律性分析提取；

8)根据提取的控制量特征规律，创建控制规律数据库；

9)通过模糊控制机制，对控制信号进行迭代计算，使其计算结果无限趋近于最佳值；

当迭代计算结果穷尽时，对计算结果进行定义误差的补偿，得到总控制规律，计算终止。

3.2 AFSMC算法下系统控制量最优计算

为了进一步提升飞机飞行过程中姿态控制量的稳定性，结合自适应滑模控制策略，设计系统在软件算法应用上选择AFSMC算法。利用AFSMC算法对飞行姿态参量的非线性结构计算，将其与运动结构动量方程进行融合，增强计算量的约束面，使其更加稳定。

通过对飞机飞行状态下，姿态调整操作的阻尼系数，结合非线性结构，可得到姿态控制器当前时间点下的运动控制方程为：

(1)

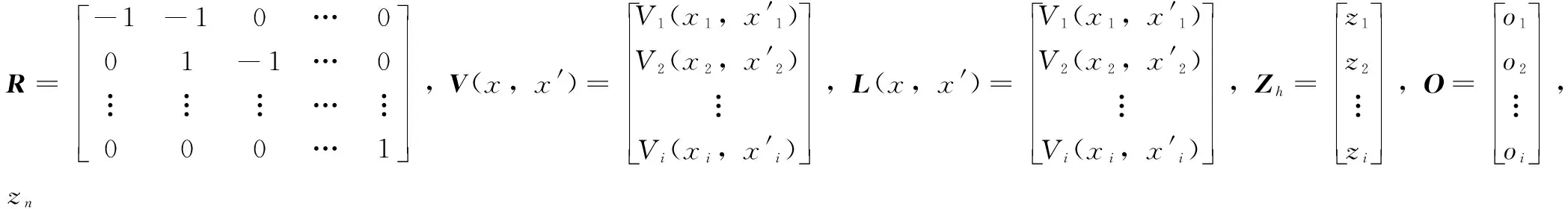
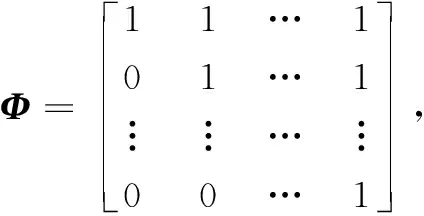
并对其求解，可得：

(2)

(3)

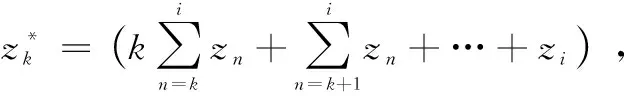
(4)

至此，飞行姿态自适应滑模控制的最优量计算结束。在计算过程中，算法用到了部分模糊计算理念[13]，通过对姿态运动变量的模糊定义使其具体化，在控制变量坐标空间中，完成最优量的计算[14-15]。基于上述特性，设计系统软件部分设计引入的算法，具有一定的鲁棒性，触发控制量优化的先决条件出发点非理想飞行姿态，因此软件部分算法能够适应各种场景下各种飞行姿态控制量的最优计算[16-17]。

软件流程如图4所示。

图4 软件流程图

如图4所示，通过c++实现软件编程，按照上述流程实现软件设计，将飞行姿态最优控制量传输至PID控制器，实现飞机飞行姿态自适应滑模控制。

4 实验结果与分析

4.1 系统调试数据场景配置

基于AFSMC算法的飞机飞行姿态自适应滑模控制系统的控制数据调试场景配置，采用仿真场景搭建+实例数据导入+测试结果对比分析的模式。通过计算机组与数据计算服务器搭建仿真调试场景硬件平台。硬件平台及软件平台配置如表1所示。

表1 仿真调试场景硬件平台及软件平台配置

4.2 仿真调试工具配置

仿真调试工具采用Automod仿真测试工具来完成调试场景的创建及调试数据的配置。在Automod仿真测试工具中创建新工程，并在工程设置项中创建DHU.SYS系统配置项，在配置项中创建调试飞机数据，生成仿真飞机模型；

定义飞机初始姿态与坐标信息；对调试场景的工程发展逻辑进行定义，并将定义的逻辑文件保存为*.BAT格式的批处理文件。至此完成仿真测试工具的配置。

4.3 仿真调试数据项目

在仿真测试工具创建场景中对表2项目进行数据调试结果采集。

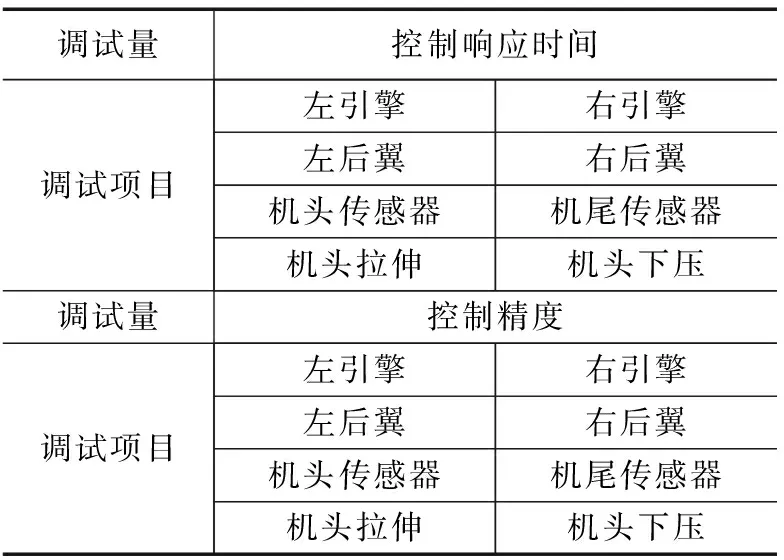
表2 仿真调试项目

根据表2调试项目，在调试场景中导入设计系统，并开始仿真调试。对应表2项目采集项目调试值，得到表3。

4.4 调试数据结果分析

将表3数据导入滑模控制精度评估模型，生成各项目控制精度图谱与系统整体控制精度图谱，如图5、图6所示。根据图谱对应数值，对调试结果进行分析。

图5(a)中，设计系统在仿真调试场景中，对飞机左引擎的滑模控制精度的浮动区间为87%～95%，最佳控制精度为95%；

表3 仿真调试项目数值

图5 各项目控制精度图谱

图5(b)中，设计系统在仿真调试场景中，对飞机右引擎的滑模控制精度的浮动区间为84%～93%，最佳控制精度为93%；

图5(c)中，设计系统在仿真调试场景中，对飞机左后翼的滑模控制精度的浮动区间为81%～98%，最佳控制精度为98%；

图5(d)中，设计系统在仿真调试场景中，对飞机右后翼的滑模控制精度的浮动区间为80%～97%，最佳控制精度为97%；

图5(e)中，设计系统在仿真调试场景中，对飞机机头传感器的滑模控制精度的浮动区间为80%～99%，最佳控制精度为99%；

图5(f)中，设计系统在仿真调试场景中，对飞机机尾传感器的滑模控制精度的浮动区间为87%～95%，最佳控制精度为95%；

图5(g)中，设计系统在仿真调试场景中，对飞机机头拉伸的滑模控制精度的浮动区间为74%～97%，最佳控制精度为97%；

图5(h)中，设计系统在仿真调试场景中，对飞机机头下压的滑模控制精度的浮动区间为89%～99%，最佳控制精度为99%；

将图5中的曲线数据作为对比指标，指标数据经过误差与扰动两组变量计算，分别以滑模控制误差分布曲线与滑模控制扰动曲线体现在图6中，通过对图6中系统整体滑模控制精度曲线分布区域与走势，可以判定：

1)基于AFSMC算法的飞机飞行姿态自适应滑模控制系统，控制误差值处于滑模控制误差分布线以上，证明系统控制误差较小；

2)基于AFSMC算法的飞机飞行姿态自适应滑模控制系统，控制曲线处于扰动曲线以上，证明设计系统具有良好的抗扰动特性；

3)基于AFSMC算法的飞机飞行姿态自适应滑模控制系统，整体控制曲线走势基本保持平稳；

经过对特殊因素的排除，得到设计系统的整体控制精度范围为90%～97.4%，根据实际飞机飞行姿态自适应滑模控制标准，设计系统符合设计标准，在标准数值下有效解决控制精度低，稳定性差的问题。

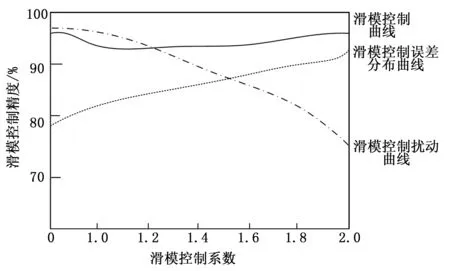
图6 系统整体控制精度图谱

5 结束语

针对飞机飞行姿态自适应控制系统存在的问题，基于AFSMC算法对控制系统进行设计。通过对PID控制器与软件算法的设计，解决传统控制系统存在的稳定性差、控制精度低的滑模控制问题。为飞机飞行姿态研究与控制系统研发，提供了数据支持。但是，在调试过程中发现，设计系统仍存在一些技术缺陷，如系统的维护问题、智能数据对接问题，有待后续新技术对其完善。