HPM视角下的高中数学新授课教学设计与反思

毛永强

体现数学的文化价值是我国《普通高中数学课程标准》的基本理念之一，随着新课程的全面实施，如何在教材中体现数学文化，如何在课堂中渗透数学文化，如何在中学数学教学中融入数学文化，受到我国中学数学教育界的普遍关注.笔者认为将数学史引入课堂是体现数学文化最有效的着力点.

本文以“等差数列前n项和公式”的教学为例，尝试如何在新授课教学中体现数学史与数学文化教育.

一、教学内容分析

“等差数列前n项和公式”是沪教版第7章“数列与数学归纳法”第二节的内容，教材由高斯求和引入，得出等差数列前n项和公式，[JP2]用高斯求和法引入一般等差数列前n项和公式，为“倒序求和法”搭建了一个十分恰当的“脚手架”.[JP]

从数学历史视角分析，等差数列前n项和公式是这样推导的吗？要让学生用好等差数列前n项和公式就必须让学生明白公式的由来以及公式背后所隐藏的数学思维过程以及数学思想方法.

基于这种想法，本案例在史料分析的基础上，依据“最近发展区”原理，从学生初中已经掌握的知识出发，探求等差数列前n项和公式.

二、史料分析与选取

两百多年前，德国数学家高斯10岁的时候，有一次老师教完加法后提出了一个问题：1+2+3+…+100=？其他同学过了很长时间才交卷，而且没有一个算对的，高斯用首尾相加的办法得出结果，这就是今天“倒序相加法”的雏形.其实，高斯并不是历史上第一个使用该方法求等差数列和的数学家，追溯历史，在高斯之前有许多智者已经推导了等差数列的求和公式，分述如下.

（1）《九章算术》成书于公元一世纪，其中有个问题：“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何？”意思是：“现有一根金杖，长5尺，在最粗的一端截下1尺，重4斤;在最细的一端截下1尺，重2斤，问依次每一尺各重多少斤？”.

（2）丢番图撰写的《论多边形数》，时间大约在公元三世纪，书中用几何方法证明了首项为a，末项为l，项数为n的等差数列之和为S=n（l+a）2.

（3）《张邱健算经》成书于公元5世纪，其中有一题：“今有女不善织，日减功迟.初日织五尺，末日织一尺，今三十日织讫，问织几何？”解曰：“并初、末日织尺数，半之，余以乘织讫日数，即得”.本题作为问题三.

（4）阿尔·卡克希撰写的《代数之荣耀》，约公元973～1048年，书中记载：1+2+3+…+n=n（n+1）2，阿尔·卡克希用倒序相加法证明了上述命题，并且把这种方法用于一般的等差数列求和，本案例将其改编为求三角形图案中宝石的个数.

（5）宋代著名数学家杨辉在《续古摘奇算法卷上》（1275年与他人合编）有一个问题：“天数一三五七九，地数二四六八十，积五十五”.求积法曰：“并上下数共一十一，以高数十乘之，得百一十，折半得五十五，为天地之数”.

这些古今中外的结论都要早于高斯对等差数列前n项和公式的探究，当然，说不定在《九章算术》之前，还有人给出了等差数列的求和公式，或者已经在应用等差数列求和公式的思想和方法解决问题，只是这些成果陨落在历史的尘埃里了.

基于上述史料分析，结合本课教学目标，设计下列教学过程.

三、教学过程设计

1.情境引入

问题1.德国著名数学家高斯10岁的时候很快就解决了问题：1+2+3+…+100=？你知道高斯是怎样算出来的吗？

问题2.下图是设计师设计的一个以宝石镶嵌的三角形图案，共有n层（见图1），请你算一算这个图案一共需要多少颗宝石？

生1：共有（1+2+3+…+n）个.

师：你能把它加起来吗？

生1：茫然……

师：我们回顾一下初中是怎样求三角形面积的？

生2：将三角形旋转倒置，与原三角形相接构成一个平行四边形，这样每一个三角形的面积是四边形面积的一半.

生2：也可以用这个方法求解前n个自然数的和.如图2，在三角形旁边倒立一个同样的三角形构成一个平行四边形，求图案中宝石的个数.

设计意图：把阿尔·卡克希记载的1+2+3+…+n=n（n+1）2的结论通过三角形图案的宝石个数直观表示出来，借用初中三角形面积的求解，既为学生搭建了合理的“学习支架”又渗透了数学历史文化.

2.公式推导

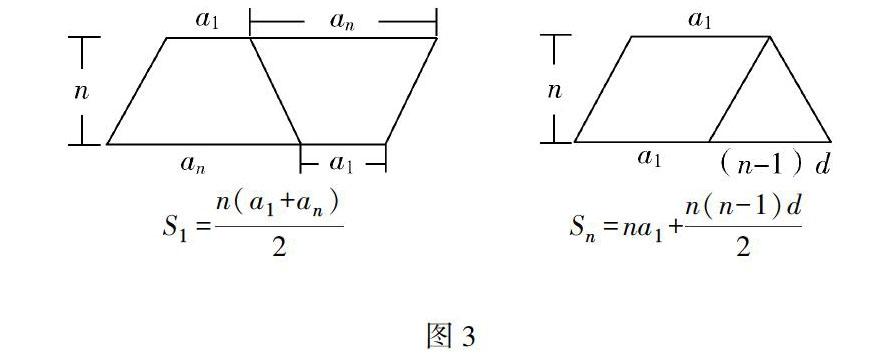
定义：数列的前n項和是把数列的前n项加起来：Sn=a1+a2+…+an.

右图“割”，即把梯形分割成一个平行四边形和一个三角形，梯形面积即为平行四边形面积与三角形面积之和.

设计意图：以形助数，借助图像加深公式记忆，给出公式的几何解释.

4.公式应用（略）

小结：本节课掌握了那些知识？用到那些方法？（学生小结师补充）

四、基于数学文化的教学反思

本案例没有照本宣科地完全按照课本内容设计，而是先对本节课所涉及的数学史进行深入研究，将其中适合本节课的内容贯穿其中，让学生既欣赏到“冰冷的美丽”又感受到“火热的发现”，具体体现在以下几个方面：

1.紧扣课标准确定位教学目标，融入数学史激发学生学习兴趣

《普通高中数学课程标准》重视数学文化在教学中的渗透，强调把数学文化融入数学教学过程中，笔者认为把数学史融入教学是渗透数学文化的有效方法之一，通过数学史寻找数学概念的发展过程，在潜移默化中提高学生的思想文化修养.基于此确定了本节课的教学目标，从两个鲜活实例引入，激发了学生的学习兴趣，如果抽去案例本身的背景，建构数学模型后发现它们是同一个问题，即等差数列的求和问题，自然过渡到本节的主题.

2.精雕细琢，挖掘数学文化素材，开拓学生数学视野

能否在数学教学中渗透数学历史文化关键取决于教师的意识，落实在于教学素材的选取，素材选取一般是通过挖掘数学历史名题，这些题目通过代代相传又经过琢磨提炼，经受了历史的检验，最终成为数学百花园中的奇花异草，也是数学文化的重要载体，就本节课“等差数列前n项和”而言，《九章算术》中《盈不足》第19题、《衰分》第1题、《均输》第17题、第18题都是很好的“学材”，《算法统宗》《张邱建算经》《孙子算经》《四元玉鉴》《洛书》都有大量关于等差数列前n项和的相关题目，本案例通过例题分析，让学生穿越时空，开拓学生数学视野，充分感受数学文化的魅力.“千淘万漉虽辛苦，吹尽狂沙始到金”，数学历史文化与数学知识相辅相成，能激发学生的学习兴趣，有效落实学生核心素养的培养目标.

3.渗透数学文化，培养学生探究能力

本案例以高斯算法为例，具体求解自然数前100项的和，以宝石镶嵌图案为背景从具体数字出发过渡到自然数n，即第1层到第n层，依据初中知识构建学习支架，即通过在三角形旁边倒立一个同样的三角形构成一个平行四边形，直观形象的说明等差数列前n项和的本质.此时，等差数列求和方法“呼之欲出”，推导更一般的等差数列前n项和公式“水到渠成”，从特殊到一般培养学生的探究能力.

HPM视角下高中数学课堂教学，为师生了解数学发展历程提供了新的思路，通过史料分析，名题呈现感受数学发展的心路历程，体验数学历史文化，有效传承人类思维方式和探索本能的血脉.