基于内聚力模型脱粘仿真的内埋芯片PI 分层研究

（江苏长电科技股份有限公司研发中心，江苏无锡 214432）

1 引言

近年来随着手持式电子设备的普及，电子设备制造商对设备内部空间利用率要求越来越高，这一需求推动着芯片封装朝越来越小型化、薄型化、高集成度方向发展。芯片埋入式封装（Embedded Chip Package，ECP）技术作为解决方案之一受到青睐。芯片埋入式封装可以使常规基板（Substrate）封装表面平铺式的贴装方式转而埋入下层基板内部，形成内外部的3D 结构，芯片不再占用基板表面积，可节省约30%的封装总面积。芯片埋入技术的设计意图是提升封装的集成度，缩小封装体积，缩短信号传输距离。伴随着市场需求的提升，对芯片埋入式封装工程问题的研究也逐渐增多。

芯片封装界面在热载荷作用下的分层失效一直是封装可靠性研究的重点问题。REN 等采用扫描电镜实验和内聚力模型仿真的方法，研究了高密度三维堆叠封装芯片之间不连续裂纹桥的复杂应力状态，并模拟了损伤起始和演化过程[1]。TAY 等通过显微镜观察了在热载荷作用下透明塑封QFN 封装形式分层的产生和扩展特征，并在有限元模型中模拟估算了界面断裂能量[2]。李晓培等对芯片埋入式封装中芯片/粘结胶界面的分层位置和界面损伤扩展问题展开了研究，并分析了芯片数量、芯片厚度、粘结胶杨氏模量等因子对分层失效的影响[3]。徐林等在塑料球栅阵列封装PBGA 的可靠性分析中引入内聚力模型（Cohesive Zone Model,CZM），对热循环作用下的SnAgCu 焊点/IMC 界面的脱层应力应变情况进行了研究，对各个界面分阶段研究了界面损伤情况[4]。刘培生等根据断裂参数-J 积分方法，仿真分析了芯片/塑封料界面的分层区域模型，探讨了温度和裂纹半径对分层的影响[5]。

前人研究分层模型失效多发生于芯片、粘结胶、焊料、塑封料之间，未有芯片重布线层（RDL）-聚酰亚胺（PI）之间的分层研究。实际上芯片封装过程中由于不同组件材料热性能和机械性能的差异，材料结合界面端都或多或少存在应力集中现象，但只会在应力最大处首先产生分层。芯片的保护材料以聚酰亚胺材料为主，在温度变化时会发生膨胀和收缩，当和其他材料热膨胀系数失配时，接触界面会发生分层或者断裂等失效问题[6]。由于芯片埋入式基板在封装过程中需经历至少一个热回流过程，此时，由于基板中ABF、Cu、PI 等材料同硅质芯片热膨胀系数具有较大的差异性，导致在高温区和降温区基板各材料之间膨胀和收缩，过程中产生的热应力影响了内埋芯片的可靠性。

本文在广泛查阅了国内外相关研究的文献后，结合实际工程问题，采用内聚力模型分析芯片埋入式封装PI 分层的问题，借助有限元仿真软件对分层失效模式进行仿真，并提出了优化设计方案。

2 界面断裂与内聚力模型理论介绍

2.1 界面断裂理论

我们把两种不同或者相同的材料，利用某种结合方式连接在一起使用的结构或组合材料称为结合材料，而其结合部称为界面[7]。界面的断裂力学主要用能量释放率或裂纹尖端的应力场和形变场来描述[8]。显然，当界面断裂能量大于结合能量，或者界面应力应变的幅度达到断裂临界点时，界面产生分层。

2.1.1 能量释放率

基于Griffith 理论，在线性弹性体中，界面断裂能量（G）等于假设某一材料内部产生长度为2a 的裂纹时消耗的内部应变能，可以表示如公式（1），其中σ 为应力，E 为杨氏模量。

2.1.2 应力强度

实际结合材料一般没有界面裂纹，但是由于在界面端具有应力奇异性(1/r1-λ)，破坏一般从界面端开始，根据界面端奇异应力场的知识，界面端附近的奇异应力可以表示为公式（2）[7]：

由于这是一个单参数场，因此，可以直观地认为存在一个与应力强度系统K 相关的临界值，当K≥KC(λ)，破坏条件达到临界值。对于单一断裂模式，应力强度和能量释放率的关系可以表示如公式（3），其中v 表示泊松比，E 为杨氏模量。

因此，界面断裂力学的两个描述准则，具有特定情况下的名义关系。

2.2 内聚力模型

界面分层可以用传统的断裂力学方法分析，也可以通过体现分离层之间牵引力的弱化关系，直接引入断裂机理，从而引入临界断裂能，也就是分离界面产生表面所需的能量。这种技术称为内聚力材料（Cohesive Zone Material）模型。

如图1 所示，界面分层可以分为3 种类型，分别为：KⅠ型，分离方向只垂直于界面的张开模型；KⅡ型，分离方向切向于界面的滑开模型；KⅢ型，分离方向在垂直/切向界面同时存在的撕开模型。

图1 断裂模型的3 种类型

对于混合模型，可以当作各种断裂模型的相互作用模型，也可分析单一分模型，本文只讨论不包含剪切力的I 型脱粘模型[9]。图2 显示了界面分层的过程。OA 段为弹性负载阶段，AC 段为弹性减弱阶段，脱粘起始于A 点，到C 点界面完全分离，应力减小为0，A点为应力最大点。根据能量释放率理论，OAC 线段的下方即临界断裂能区域，通常为OB 这种某一斜率的线性增长能量。

图2 法向接触应力与接触间隙关系曲线[10]

3 PI 分层的内聚力模型脱粘仿真

3.1 实例介绍

埋入式封装结构由芯片埋入式基板、被动元件及塑封材料组成。当表面焊接元件时需要过回流炉，回流炉温度最高能达到260 ℃，在升温与降温时芯片埋入式基板内层材料由于热膨胀系数不同，结合界面承受不同的热应力，当脱粘能量达到材料分离临界点时将发生分层。本文重点研究芯片埋入基板内层的应力分布，如图3 所示为实验样品结构示意图。图4 为实验产品经过回流炉（最高255 ℃）之后的切片图，实验显示埋入芯片RDL 铜层与上层PI 之间在T0产生了裂纹，可能会影响产品可靠性。

图3 芯片埋入式封装堆叠结构示意图

图4 分层切片扫描电镜图

3.2 模型建立

进一步实验排除了其他因子影响，发现埋入芯片分层只与基板材料和热制程相关。由于基板在水平方向上的长度和宽度远远大于垂直方向上的厚度，材料结合处产生的应力等于剪切力和剥离力之和[11-12]，所以为了便于分析，模型做如下假设：

1)简化为只存在法向形变而忽略切向应力应变；

2)模型为各向同性完全弹性体，即服从胡可定律，而且弹性常数不变；

3)模型处于均匀温度场，且温度在结构上均匀分布；

4)忽略模型中的湿气膨胀应力和材料性状变化，只考虑形变产生的应力。

由于整条基板建模数据太大，为减少计算，模型只截取基板带芯片位置的一小块区域，包含芯片、重布线层（RDL）、绝缘层(ABF/PI)、铜柱和线路层特征，模型尺寸1 mm×0.5 mm，Dvia=0.05 mm，pad 尺寸为0.8 mm×0.4 mm。如图5 所示，基板为上下对称结构，中间绝缘层ABF 之间埋入芯片。又由于模型对于铜柱呈四边对称结构，模型进一步简化为四分之一模型，如图6 所示。

图5 芯片埋入式基板简化模型

图6 基板四分之一简化模型

3.3 仿真分析

ANSYS 是业界优秀的静力学有限元仿真软件，本文借助ANSYS Workbench 模拟基板模型在热载荷下的变化过程。通过查询材料手册，模型中涉及的材料属性如表1 所示。

实验回流炉的温度作为热载荷如图7 所示。

模型边界条件为底部三端点约束，A 端点限制全部X、Y、Z 方向位移，B 端点X 方向自由,C 端点Y 方向自由，假设基板各材料零应力温度为125 ℃，网格划分规则六面体采用扫掠，无法扫掠的采用四面体，在重点关注的芯片上层材料网格细化，共612397 个单元，如图8 所示。

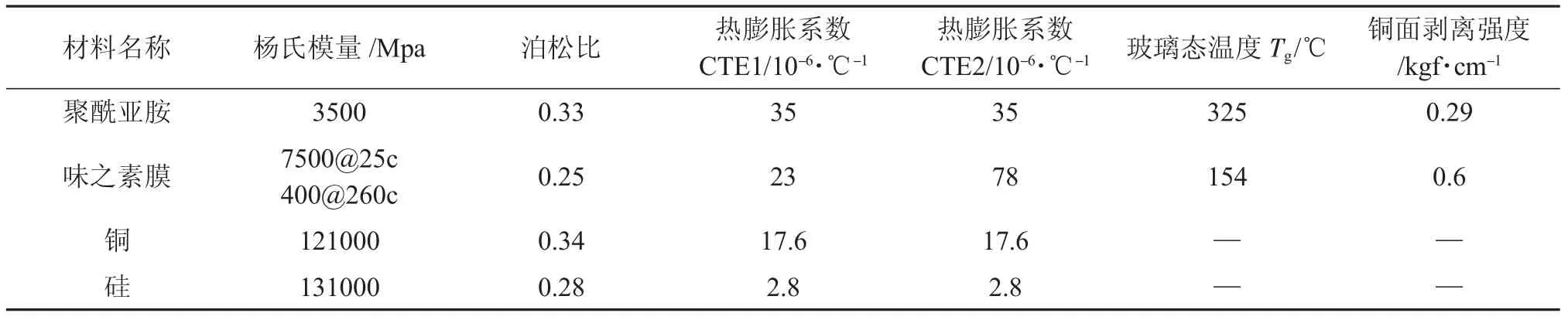
表1 材料参数[13]

图7 回流温度载荷曲线

3.4 仿真结果与实验对比

3.4.1 热应力仿真

求解不同温度下的模型von-Mises 等效应力最大值，如图9 所示，当温度为250 ℃时，模型的热应力最高。

进一步分析芯片PI 层应力应变情况，仿真结果如图10 所示，可见在PI-RDL 结合边缘处具有应力最大值，形成应力集中，可能导致界面分层。

3.4.2 内聚力模型的脱粘仿真

脱粘模型基于能量释放率，根据表1，聚酰亚胺(PI)与铜面的剥离强度为0.29 kgf/cm，换算为临界断裂能为284.2 J/m2。仿真结果显示，模型在升温至250 ℃之前未发生分层，在降温区逐渐发生分层，并至25 ℃达到最大值。分层模型如图11 所示，界面分离距离不足1 μm，与图4 实验结果一致。该仿真为I 型法向脱粘模型，忽略了实际中存在的表面粗糙度和机械结构力等影响结合力的因子。

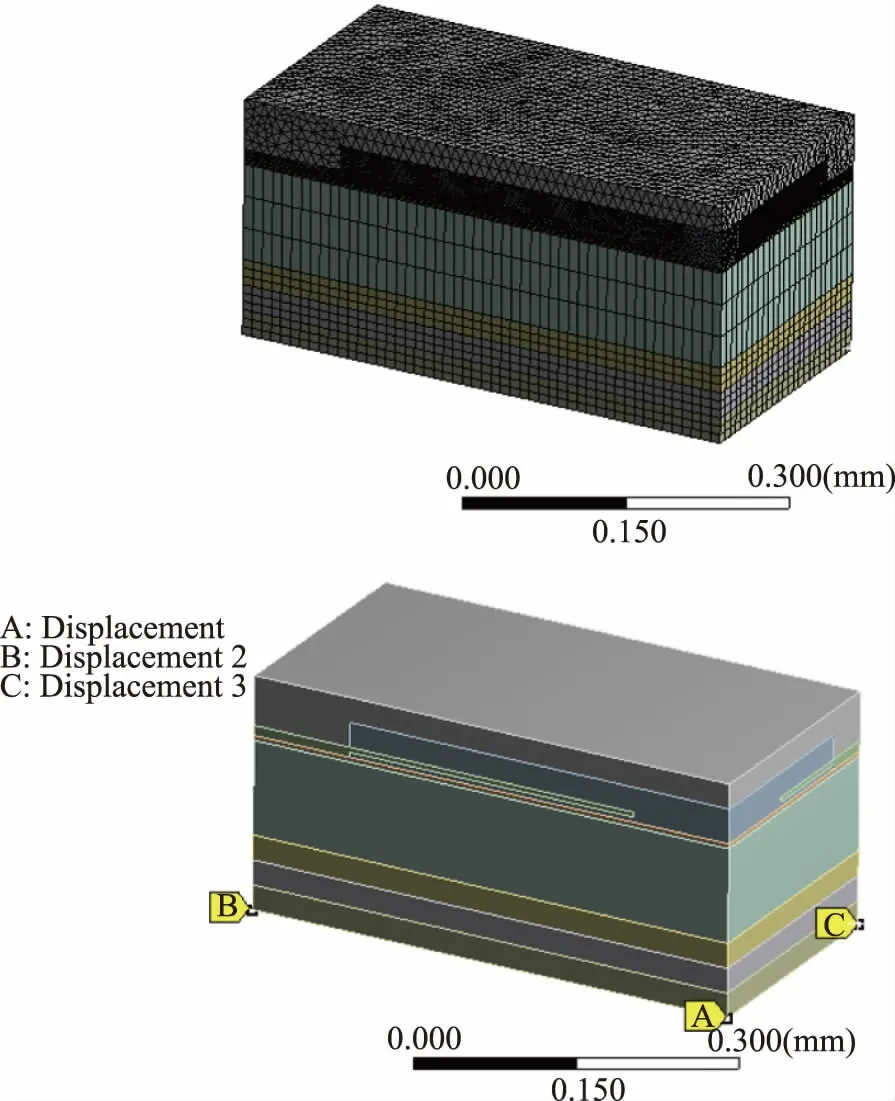
图8 模型网格划分

图9 应力-温度仿真结果

图10 模型整体与PI 局部应力-应变云图

图11 PI 与铜界面分层仿真

3.4.3 材料厚度优化方案仿真

实验还针对应力集中区域PI 和其上铜线路的厚度变化对von-Mises 应力最大值的影响进行了仿真。结果显示，较厚的PI 和较薄的铜厚可以减少应力值，但影响不明显（大约9%），数据如图12 所示。

图12 材料厚度对应力的影响对比

4 总结

论文通过ANSYS 有限元仿真软件，建立芯片埋入式封装基板模型，并模拟封装热制程环境，对材料界面分层位置和过程进行了模拟仿真。仿真结果表明，材料供方提供的材料在铜面剥离强度规格达不到工艺需求，在回流降温区域会产生分层，等效应力最大值在PI 与铜结合的边角处，约为121 MPa。仿真结果同时表明材料厚度和线路厚度对热应力的影响空间较小。分析结果能够对芯片埋入式封装开发材料选型和实验计划提供参考。