基于复杂网络社团相似度的电网分区研究

凌汝晨，邵卜琳娜，李 牧，陈鑫磊，操晨润，薛 超

（1.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314000；2.国网浙江平湖市供电有限公司，浙江 嘉兴 314200；3.国网浙江海盐县供电有限公司，浙江 嘉兴 314300）

0 引言

科学研究结果表明，现实世界中的网络以复杂网络的形式存在[1]，其具有一种社团结构特性，该特性表现为“社团内部的联系较为紧密，社团之间的联系较为稀疏”。电力网络也是一种典型的复杂网络[2]，为了实现对电网运行状态有效、快速的组织、调度和指挥，提高电网运行的安全性能，要求电网实现分层、分区运行。目前，电网分区方案的形成常根据行政区域或所属电网公司划分，已经不适应新能源的大规模接入、直流送出或馈入等复杂的电网运行环境。结合复杂网络理论进行研究，已成为解决日益复杂的网架结构下电网分区的新思路。

电网电压-无功分区控制领域已经成功应用复杂网络社团结构理论进行电网分区研究。其传统方法[3]利用反映电网各节点之间耦合程度的电气距离矩阵对电网进行分区，但被控节点无法确保划分到电气距离最近的无功源节点所在的区。文献[4]基于电气距离矩阵，提出一种映射分区方法，保证了这一无功电压分区的基本要求。而通过引入复杂网络理论中的模块度概念[5]，文献[6]基于复杂网络加权模块度，提出了一种先分裂后凝聚的电网分区方法，解决了最优分区数确定的问题，最终分区结果具有较好的社团结构特性。文献[7]采用社区网络挖掘算法进行分区，然而由于算法的局限性，该方法不能应用于大规模网络，且未解决最优分区数的问题。文献[8]将电网等效为无权无向复杂网络，以图论方法实现网络区域划分，但其忽略了电网的运行特性，不符合如今电网运行状态的复杂现状。文献[9]利用潮流和线路阻抗作为边的权重，用4 种不同模型对算例进行仿真，验证了社团结构在电网分区中的作用，但并没有结合电网分区的实际应用场景进行验证分析。文献[10]所提出的电磁环网分区解环方法所产生的每个分区都可形成以2～3 座500 kV变电站为核心的供电方式[11-12]，考虑了更多的实际情况，以确保分区解环后电网的供电安全性，故而优越性更高。

综上所述，研究人员已经将许多复杂网络社团发现算法运用到了实际电网分区之中。然而，目前的电网分区方法并未涉及基于节点相似度的社团挖掘算法这一类比较重要且有效的算法。文献[13]提出一种节点相似度模型，并采用迭代的思想进行社团划分，可应用于大规模网络中。文献[14]提出节点相似度模型，进而提出簇相似度模型，采用层次聚类算法，以社团平均相似度S为指标确定最优分区数。文献[15]提出加权网络中基于节点相似度的社团划分的算法，并利用Zachary 空手道俱乐部网络[16]算例验证了所提算法的有效性。可见，相似度函数能够普遍应用于大规模复杂网络划分，实现复杂网络社团快速挖掘，故将相似度概念应用于大规模电网的分区也可以实现电网快速分区。

本文利用复杂网络相似性对实际电网的社团结构进行分析，提出一种基于相似度的电网分区新方法，并采用IEEE 39 节点算例和某地区220 kV 电网进行仿真分析。仿真结果表明，基于本文方法所得到的分区方案是正确且有效的。

1 基本概念

复杂网络相似度的研究广泛应用于网络社团结构。利用所定义的网络节点相似度矩阵，将相似程度高的节点分配到一个区，可以大大降低算法的复杂性。电力网络是一种加权复杂网络，而本文定义的相似度函数能够应用于加权网络。

1.1 节点强度

对于一个具有n 个节点和m 条边的网络G（V，E），边eij的权值为wij，当节点i 和j 不相连时wij=0，那么节点i 的强度定义为：

式中：V 为节点的集合。

在无权图中，当节点i 和j 相连时，wij=1，否则wij=0。此外，本文将节点i 的单位强度u（i）定义为与该节点相连的所有边权重的平均值，即：

式中：k（i）为节点i 的度。

1.2 共邻节点

若节点z 同时与节点i 和j 相连，则称节点z为节点i 和j 的共邻节点。定义共邻节点作用系数εz（i，j）为2 个节点i，j 与其共邻节点z 的2 条连边的权重和与节点z 对与其全部相邻节点连边的权重和之比，即：

定义共邻节点连接强度Sz（i，j）为该共邻节点z 的单位权重与其作用系数的乘积，即：

共邻节点连接强度Sz（i，j）的含义是节点z对与其相连的2 个节点i，j 相似性所作的贡献，Sz（i，j）的值越大，则节点i，j 的相似度越高。

1.3 节点对边权强度

当2 个节点相连且不存在共邻节点时，2 个节点仍应当存在一定的相似度。此时，采用节点对边权强度描述节点相似度，定义节点对边权强度sw（i，j）为：

由式（5）可以看出，节点对边权强度sw（i，j）能够衡量2 个节点i，j 之间连边的权重在与2 个节点全部相邻节点连边的权重总和中的占比。该值越大，则说明节点间i，j 连接的紧密性越强，相似度越高。

1.4 节点相似度

若2 个相连节点之间存在共同邻居，则定义节点相似度为该节点对所有共邻节点连接强度之和。若2 个相连节点不存在共同邻居，则采用节点对边权强度定义节点相似度。若2 个节点之间不存在连边，则令其相似度为0。因此，本文定义节点相似度为：

式中：Γ（i）∩Γ（j）表示节点i，j 的共邻节点的集合。

1.5 社团相似度

本文在节点相似度的基础上，进一步提出利用社团相似度评估不同社团间的相似度。首先，同一个社团内部节点的相似度应当大于不同社团间的相似度。现假设有2 个社团C1和C2，则计算社团C1中所有节点与C2中所有节点之间的相似度平均值，即：

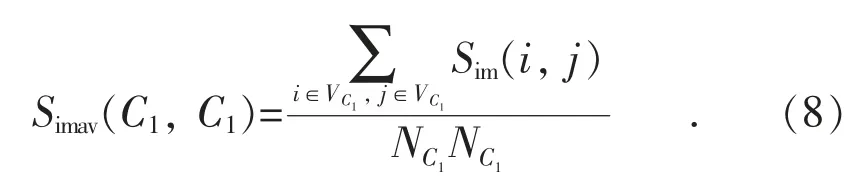
而本文将社团相似度定义为：社团C1和C2之间的相似度平均值分别与单个社团内部节点的相似度平均值的比值之和，即：

1.6 模块度

为了衡量社团划分的优劣程度，Newman 等人引入了模块度Q 的概念用于评价加权网络[17]，使模块度概念更具有实际意义，加权模块度Q 的定义为：

式中：Aij为节点i 与j 之间的权重；为与节点i 相连的所有边的权重之和；为网络中所有边的权重之和。模块度值的大小主要由网络的社团划分状况决定，能够定量衡量网络社团划分优劣。若模块度的值越接近1，则表明划分出的网络的社团划分质量越好。因此，本文以模块度Q 最大来得到最优的电网分区结果。

2 分区算法

基于加权相似度指标的定义，采用层次聚类的思想，本文提出基于相似度的加权网络电网分区算法。算法具体步骤分为预分裂和分区凝聚。

步骤1：利用式（9）计算出节点相似度矩阵，并从第1 个节点遍历到第N 个节点，将与节点i相似度最大的节点j，以及这2 个节点所属的社团编号C 储存到一个三元组SV中，初始状态下所有节点的社团编号为0，表示节点未编入社团。

步骤2：从SV中任选一对尚未合并的节点对，即SV中存储的社团编号为0，将该节点对合并为新社团，并指定节点对中第2 个节点前编号为当前节点。若SV中所有的社团编号均不为0，则预分裂结束，所有节点均已并入社团。

步骤3：选择当前节点在SV中对应的行，若该行社团编号为0，则将该行第2 个节点与当前社团合并，并指定其为当前节点；若该行的社团编号不为0，则转步骤5。

步骤4：重复步骤3。

步骤5：若该行的社团编号与当前社团编号相同，则表明当前社团已经包含了第2 个节点，转入步骤1；若该行的社团编号不为当前社团编号，则将2 个社团合并，再转入步骤2。

步骤6：由式（9）计算出所有社团间的社团相似度，并根据式（10）计算当前社团划分的模块度指标。

步骤7：将社团相似度最大的2 个社团合并。

步骤8：重复步骤6 和7，直到所有社团合并成1 个。

其中，步骤2 到步骤5 将网络使用相似度矩阵进行预分裂，使得相似度高的节点合并到一个分区。步骤6 到步骤8 为分区凝聚过程，通过将社团相似度高的2 个社团合并，并使用模块度指标确定最优分区个数。

3 算例分析

3.1 IEEE 39 节点系统

本文以IEEE 39 节点系统为例，对所提出的基于复杂网络相似度的电网分区方法进行仿真分析。将系统中的电源、负荷视为节点，将节点之间的线路视为边，这样就可以把实际网络抽象成复杂网络进行分析。

本文从复杂网络理论角度去研究电网分区，无法避免的是权重的选择问题。在选择权重时，应根据实际需求选择不同权重。由相似度概念可知，本文在选取权重时应采用相似权。本文选择3 种权重模型来建模，并进行对比分析：模型1不赋权，将线路权重取1，即权值矩阵为邻接矩阵；模型2 利用线路电抗的倒数1/Xl作为权重，线路电抗在一定程度上可以反映节点之间的电气距离；模型3 将线路有功潮流Pl作为网络权重。针对IEEE 39 节点，3 种模型的分区结果分别如图1—3 所示。并将本文3 种模型的分区结果与文献[4]、文献[9]模型4 分区结果进行对比。采用5 种方法的IEEE 39 节点系统分区结果如表1 所示。

图1 采用模型1 时的IEEE 39 节点系统分区结果

本文模型1—3 分区结果的模块度指标分别为0.59，0.65，0.72，模型2 和3 的模块度指标大于模型1，说明将网络加权可以使得社团结构更加明显。

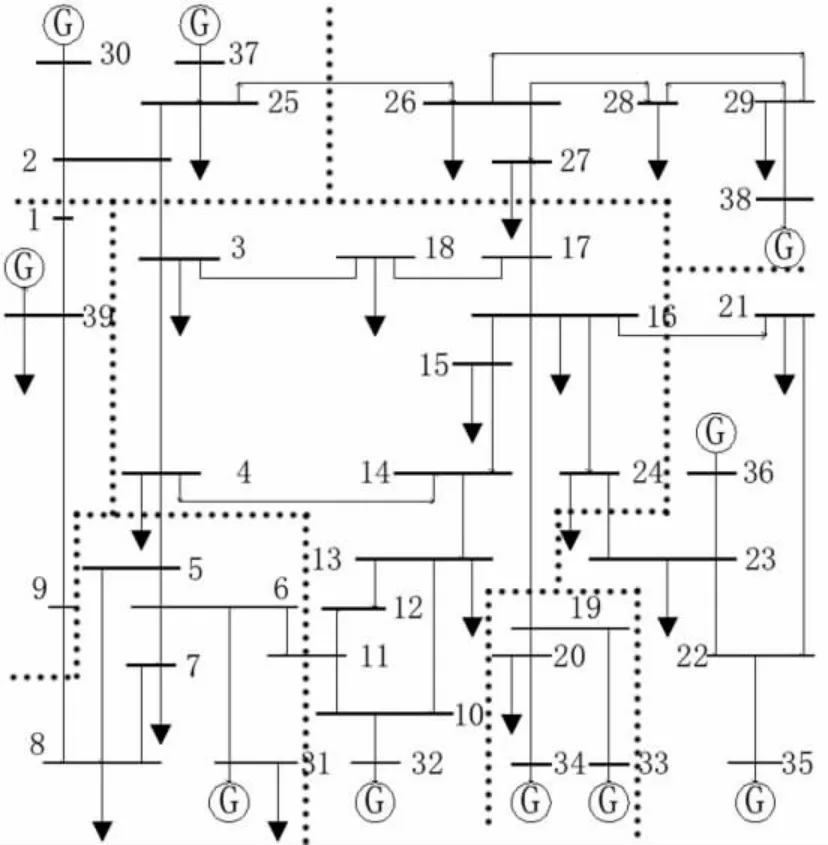
图2 采用模型2 时的IEEE 39 节点系统分区结果

图3 采用模型3 时的IEEE 39 节点系统分区结果

文献[4]采用电气距离矩阵进行无功电压控制分区，其分区结果在一定程度上体现了电气联系。由表1 可知，与本文模型2 对比可以看出，2个分区结果中，有几个分区完全相同，其余分区也存在相似性，且满足无功分区的要求，说明采用线路电抗的倒数1/Xl作为权重应用于无功电压控制分区是合理有效的，2 种方法都在一定程度上反映了电网的线路参数特征。但文献[4]分区结果的模块度指标只有0.529，低于本文模型2 分区结果的模块度指标0.65，说明本文模型2 具有更好的复杂网络社团结构特性，从复杂网络模块度指标角度来看，本文结果更合理。

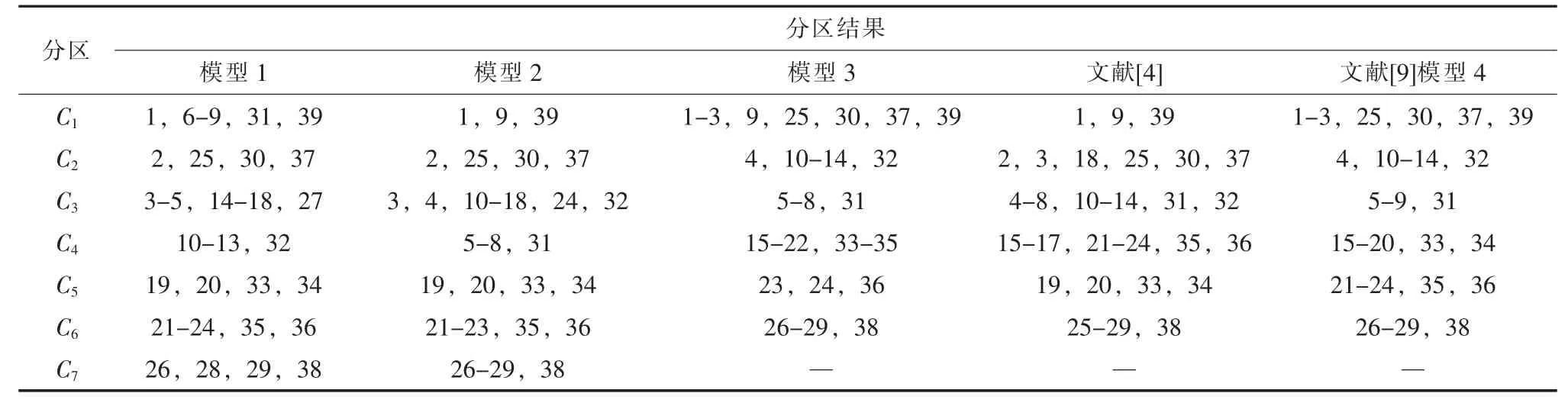
表1 IEEE 39 节点系统分区结果对比

本文模型3 将相似度大的节点划分到同一分区，使得区域内节点潮流交流更加紧密，分区间的潮流交流比较小，这与实际电网中500 kV/220 kV 输电网络的情况较为类似，500 kV 网络作为输电主干线路，各分区间220 kV 线路上的潮流不会很大。可利用文献[9]模型4 采用Louvain 改进层次算法，将线路潮流作为权重，快速挖掘电网中的社团，其分区结果与本文模型3 较为相似，从侧面反映了本文方法的合理性。因此，本文模型3 选取权重的方法可以应用到电磁环网分层分区中。

由表1 可以看出，本文分区方法与文献[4]、文献[9]模型4 分区方法所得到的最终分区结果有相一致的地方，比如本文方法所得到的分区C5和文献[4]方法所得到的分区C5相同。本文方法所得的C2和文献[9]模型4 所得的C2相同，这是因为本文方法和其他2 种方法都在一定程度上反映了电网的线路参数特征，这证明了本文方法的有效性和正确性。与文献[4]方法所得到的分区结果相比（其加权模块度值为0.529 0），本文方法更明显地体现了网络的社团特性。

3.2 某地区220 kV 电网分区

虽然本文电网分区方法的有效性在IEEE 39节点系统算例上得到验证，利用实际电网进一步验证本文方法的有效性仍然很有必要。本文将文献[10]的某地区220 kV 电网作为算例，考虑电网实际情况，合理控制分区规模，将分区规模限制在3 个分区，采用本文模型2 和模型3 对该电网分区结果的网架结构如图4 和图5 所示。本文模型2 和模型3、文献[4]、文献[10]模型分区结果对比结果如表2 所示。

图4 采用模型2 时的某地区220 kV电网分区结果

图5 采用模型3 时的某地区220 kV电网分区结果

由表2 可以看出，4 种不同方法分区结果中分区C3是完全相同的，而分区C1和C2存在差异。本文模型3 和文献[10]分区结果完全相同，都表现出了较强的社团结构特性（模块度指标分别为0.615 和0.622），不同分区间的电气联系、功率交换都比分区内的电气联系、功率交换小。若断开区域间的线路，对各分区正常运行影响较小，满足电网分层分区要求，分区结果比较合理。而本文模型2 中将节点1 与节点30、节点33与节点34 分到不同分区，若断开区域间的线路，将形成串供结构，存在影响电网正常可靠运行的危险。因此，选取合适的权重对分区结果的合理性存在影响。

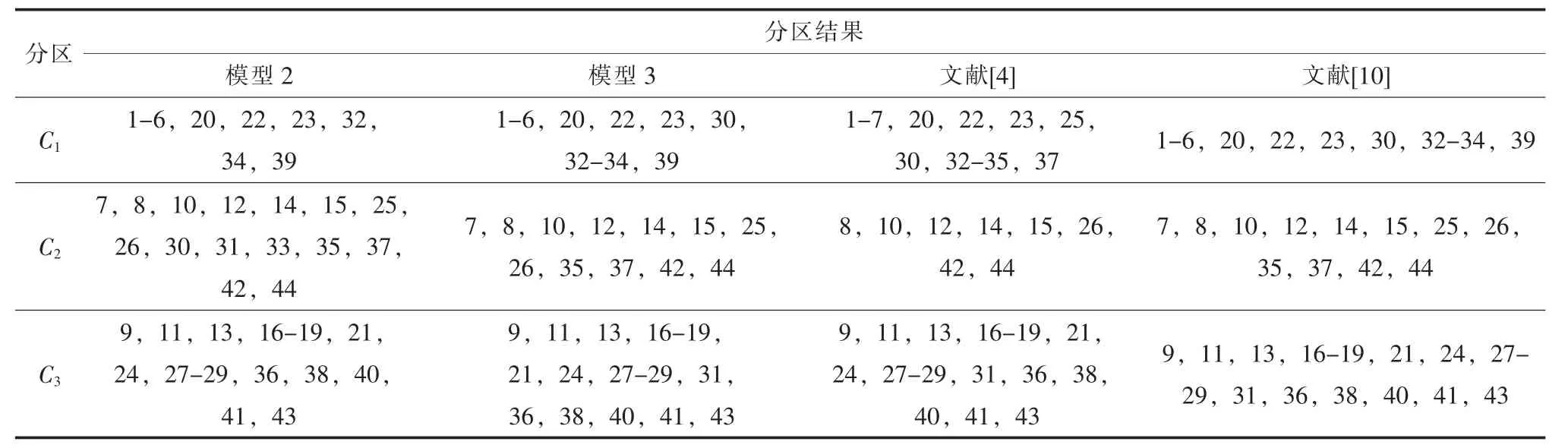
表2 某地区220 kV 电网分区结果对比

采用文献[4]映射分区算法得到的分区方案中只有节点10 中的2 台主变压器对分区2 供电，500 kV 主变压器的容量不够充足，模块度指标为0.534，社团结构特性不够明显。本文方法更侧重于将节点相似度高的节点分配到一个区域，使得分区内相似度更大，分区间相似度更小，分区速度较快，可以快速得到较强社团结构特性的分区结果。

4 结语

本文基于复杂网络相似度，提出了一种电网分区方法，定义了加权电网的相似度矩阵和社团相似度的计算方法。首先，利用节点相似度将各节点预分裂；然后，将社团相似度大的社团合并凝聚分区；最后，利用模块度指标确定最优分区个数。

采用不同的赋权方法可以使分区具有不同的意义，本文采用3 种模型对电网赋权。IEEE 39节点系统算例仿真结果表明：当选取线路电抗的倒数作为权重时，本文方法可以应用于无功电压分区；而选取线路潮流作为权重时，本文方法又适用于电磁环网分区，且分区后网络表现出良好的社团结构特性。某地区220 kV 电网算例仿真结果表明，通过选取合适的权重（线路潮流），本文方法可以有效快速地实现真实电网分区。因此，本文方法具有广泛的应用前景。