变量世界，让思维方式发生深度转变和进阶——《变化的量》教学实录

文|董文彬

【教学内容】

北师大版六年级下册第四单元第1 课时。

【教学过程】

一、旧事重提，生发新的思考

师：乌鸦喝水的故事我们已经很熟悉了，从数学的角度思考，哪些量在发生变化呢？是怎样变化的？

生：瓶子里水面的高度在发生变化，水面升高了。

生：石子数也在发生变化，石子数变多了。

师：这两个量都在发生变化，它们之间有联系吗？是谁的变化引起了谁发生变化呢？

生：有联系，石子数的变化引起水面高度变化。

师：看来，任何变化的背后都是有原因的，这里水面高度与石子数的变化就是有关联的。今天这节课，我们就带着关联的眼光来一起认识变化的量。

二、寻索变量，体会变化关系

情境一：淘气打字。

师：这是淘气打字时的字数变化情况。观察表格，想一想，哪些量在发生变化？

生：时间在发生变化。

生：字数也在发生变化。

师：能试着描述一下它们是怎么变化的吗？

生：时间增加，字数也增加。

师：这两个量的变化之间有联系吗？

生：字数随着时间的增加而增加。

师：（出示下图）淘气打字时的字数变化情况还可以用这幅图来表示。（描点、连线）从图中你还能看出“字数随着时间的增加而增加”的情况吗？从哪能看出来？

生：图中的这条线在不断上升，表示时间增加，字数也在增加。

师：如果这样竖着画一条直直的线，也能表示字数在上升吗？

生：这样画不行，这样画字数是在增加，但时间就是不变的了，这里时间也是增加的。

师：也就是说，只有像这样一条上升趋势的线才能表示出字数是时间关联着变化的，对吗？

师：从刚才淘气打字的情境中，我们发现了一个量随着另一个量的变化而变化，像这样的相关联变化的量在生活中还有很多，我们接着看。

情境二：摩天轮转动。

师：（出示摩天轮图片）一个人坐在某个座舱里随摩天轮转动时，有没有相关联的变化的量呢？

师：是哪个量随着哪个量的变化而发生变化呢？

生：座舱在圆周上的位置，随着时间的变化发生变化。

生：路程在随着时间的变化而变化。

师：你说的路程指的是什么？

生：就是座舱在圆周上转过的距离。你看座舱从最低点开始计算，随着时间的增加，座舱在圆周上转过的距离也在增加。

师：他从另外一个角度又找到了一组新的变化的量。

生：角度随着时间的变化而变化。就是假设座舱从最低点开始，从圆心往下画一条线，随着时间的增加，摩天轮在转动的过程中，座舱与圆心的连线就会转过一个角度，这个角度在随时间而发生变化。

师：很好，又是一组新的变量。

生：随着时间的变化，座舱离地面的高度也在发生变化。

生：我认为座舱的高度也在随着角度的变化而发生变化。

师：刚才有人提到了座舱高度随着时间在发生变化，它们具体是怎么变化的呢？以摩天轮转一圈为例，能描述一下吗？

生：座舱从最低点开始随着时间先是越来越高，到达最高点之后，随着时间再逐渐下降，最后回到最低点。

生：也就是随着时间的增加，座舱的高度先升高后降低。

师：（出示空白方格图）如果我们把这个变化过程表示在这个方格图上，是这样的变化趋势吗？（出示“转1 圈”的图象，如图）和你刚才想的一样吗？

生：是，一样。

师：从图中你能进一步获取到哪些信息？

生：最高点高度是18 米，最低点高度是3 米。

生：转动一圈的时间是12 分钟。

生：1～6 分钟座舱高度在增加，6～12 分钟座舱高度在降低。

师：这是摩天轮转一圈的情况，如果摩天轮再转一圈，图象会怎么样呢？

生：和第1 圈一样。

师：（出示“转第2 圈”的部分图象）座舱第一次到达最高点以后，再一次达到最高点需要经过几分钟？

生：12 分钟。

师：你是怎么得到的？

生：第一次到达最高点是12分钟，第二次到达最高点是24 分钟，两次的时间间隔是24-12=12（分钟）。

师：如果再转一圈，图象接下来会怎么样呢？

生：和前面一圈一样，先升高后下降。

师：如果摩天轮就这样一圈一圈一直转下去，图象就会———

生：和前面一样，先升高后下降，再升高再下降，不断重复。

师：也就是说，随着时间不断增加，座舱高度就会“升高—下降”不断循环往复进行，图象也会这样“升高—下降”不断循环往复出现。

师：座舱高度随时间发生的这种变化叫什么变化？

生：周期。

师：对，叫“周期性”变化。在这里，摩天轮转一圈的周期是多长时间呢？

生：12 分钟。

三、丰富素材，再度寻索描述变量及变化关系

1.回应前测，关联描述变量。

师：刚刚我们通过“淘气打字”和“摩天轮转动”两个情境发现了其中存在的相关联的变化的量以及两个变量之间的变化关系。在课前，有很多同学也找到了生活中存在的一些变化的量，我们来一起看一看。

出示：

师：有人认为“身高”是变化的量，同意吗？

生：同意。

师：你能想到身高是随着哪个量在发生变化吗？

生：年龄，随着年龄的增长，身高也会增加。

师：身高会随着年龄的增长而一直增加下去吗？

生：不会，当一个人的身高长到一定高度的时候，随着年龄的增长，身高就不再长了，会保持那个高度不再变化。

师：也就是说，人的身高随着年龄增长而增加这件事只发生在某个阶段，超过特定年龄段这个规律就不存在了。

出示：

师：也有人认为“温度”是变化的量，同意吗？

生：同意。

师：那么温度是随着哪个量在发生变化呢？

生：时间，一天中从早到晚，温度会随着时间的变化而变化。

生：季节，随着季节的更替变换，温度也会发生变化。

生：环境，环境发生变化，温度也会发生变化。

生：纬度，从赤道到北极，温度会随着纬度的变化而变化。

生：海拔，随着海拔的升高，温度会逐渐下降。

师：真是太棒了！你们仅仅从看到“温度”这个变量，就能联想到这么多与它相关联的其他变量。

2.补充素材，寻找描述变量。

出示：

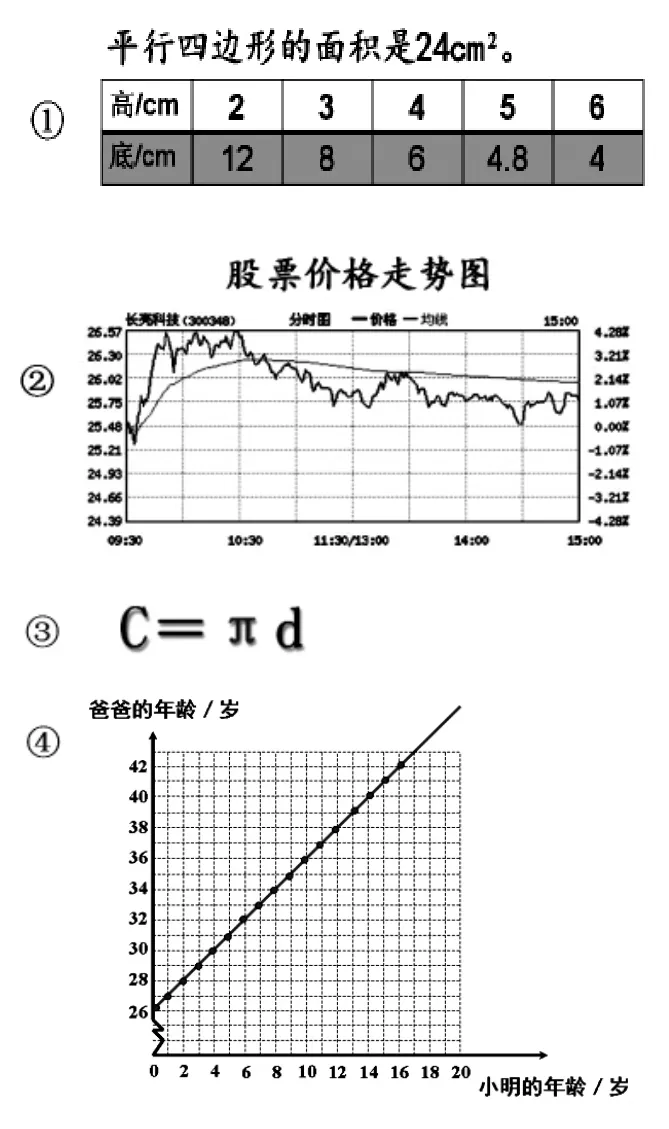
出示小组活动要求：

a.找出每个情境中有哪些相关联的变化的量？

b.描述清楚一个量随着另一个量的变化而发生了怎样的变化？

组1：

生：我选择①号情境，变化的量是平行四边形的底和高，随着高的不断增加，底在不断减少。大家有什么问题吗？

生：我的想法和你一样，我补充一点，平行四边形的高增加，底就减少，方向是反着的，但这个过程中，平行四边形的面积一直是24cm2，保持不变。

师：你还看到了变化中不变的东西，好眼力！

生：我选择③号情境，变化的量是圆的周长C 和直径d，随着d的不断增加，C 也在不断增加。

组2：

生：我选择②号情境，变化的量是股票的价格和时间，随着时间的增加，股票的价格先下跌再升高、升高，再下跌，再升高，又下跌、又升高……股票的价格随着时间的增加呈现波动变化。

师：“波动”这个词形容得好！

生：股票价格随着时间的增加一会儿升一会儿降，好像没有什么规律。

生：我还找到一组变化的量是股票的价格和均线，股票的价格随着均线的变化而变化。

生：我有不同意见，我认为均线是随着股票的价格的变化而发生变化，而不是股票的价格随着均线的变化而变化。

生：应该是股票的价格随着均线的变化而变化吧？

生：什么是均线？我认为均线应该是这只股票的平均价格，应该是股票在这段时间的价格变化引起平均价格的变化，而不是平均价格引起股票价格的变化。

师：理不辩不明，你们理解得很深刻。

四、全课小结（略）