Simulation of proton-neutron collisions in inverse kinematics and its possible application

Bi-Lu Li· Gang-Lin Yu · Shi-Fei Shen

Abstract Neutrons have played a vital role in many nuclear physics fields. In some cases, the inverse kinematics of neutrons colliding with other nuclei are also worth studying. In this study, the inverse kinematics of thermal neutrons colliding with high-energy protons is simulated by using the Monte Carlo method. Thermal neutrons are taken as target particles, whereas protons are incident particles. The simulation implies that, after collision, the energy of the output neutron at 0° equals the energy of the incident proton.A possible application of the result is proposed that might yield single-energy neutrons.Some key parameters of the conceptual design were evaluated, demonstrating that the design may reach high-neutron-energy resolution.

Keywords Inverse kinematics · Mono-energetic neutron ·Proton · Monte Carlo

1 Introduction

1.1 Neutron-induced reactions in inverse kinematics

The neutron transport method plays an essential role in neutron physics [1]. In many technological applications,such as the study of reactor physics [2] and nuclear fuel burnup analysis [3], the neutron transport method needs to be applied in simulations and calculations. The collision model in neutron transport often focuses on the process of neutrons impinging on a target where the target nucleus is considered at rest[4].In some cases,the inverse kinematics[5] of neutrons colliding with nuclei is worth of studying.In one case, the reaction cross sections were measured for the interaction between neutrons and radioactive isotopes and short-lived particles.In such a situation,it is difficult to prepare the target sample, place it near the detector, and perform the measurements[5].However,the cross sections of neutrons with short-lived particles are required in many applications, such as in astrophysical s-[6], r-[7], and pprocesses [8], and in nuclear physics phenomena such as those involved in the disposal of radioactive waste[9].One way to solve the problem of short-lived isotopes is to apply inverse kinematics [5].

1.2 Monoenergetic neutron sources

When studying neutron reactions, there are two main methods to obtain monoenergetic neutrons, one using time of flight (TOF) and the other using accelerator-based monoenergetic neutron sources [10].

The TOF method can yield energy spectrum information of neutrons through measurements of the neutron flight time over a path length[11].The TOF method is simple in terms of data processing and offers excellent performance in the low-energy(eV)region with a high energy resolution of up to 0.1%[12].Although an energy resolution of 0.53%can be acquired for 1-MeV neutrons in EAR1 [13, 14]without regard to the energy spread of the proton beam,the neutron flight path of this facility is 185 m. It is costly to build such large facilities. With the increase in neutron energy,the energy resolution of the TOF method decreases as the TOF is extremely short. Owing to the high speed of neutrons with high energy, long-distance flight paths and substantial shielding are necessary to achieve higher energy resolution [15]. At the same time, higher requirements are imposed on other devices, such as high-performance accelerators with large beam currents and narrow pulse widths, as well as fast detectors and fast electronics[16]. Consequently, it can be difficult to improve the energy resolution in the TOF method for high-energy(keV)neutrons [16].

Another method of obtaining monoenergetic neutrons is to use an accelerator-based monoenergetic neutron source,which accelerates charged particles to a specific energy,and then bombarding the target with charged particles to generate neutrons by nuclear reactions. The energy of neutrons emitted at a specific angle can be calculated based on the laws of energy and momentum conservation [17].Generally, accelerator-based neutron sources can be applied to obtain neutrons ranging in energy from MeV to tens of MeV. The generation of keV-order monoenergetic neutrons is realized through large-angle scattering, which usually has a meager yield [10]. Different neutron energy zones correspond to different types of reactions. Sometimes, the requirements for energy adjustment, neutron intensity and monochromaticity cannot be satisfied by one type of accelerator and one nuclear reaction [18–20].

An increasing number of applications and studies have employed higher requirements for monoenergetic neutrons[21], for instance, the measurement and evaluation of neutron–nucleus reaction cross sections. Many reactions between heavy nuclei and neutrons are of great importance in nuclear reactors. However, the cross sections of many neutron-heavy nucleus reactions in the resonance region from keV to MeV display complicated structures.There are many difficulties in the direct measurement of resonance parameters because the widths of resonance structures are of the order of several electron volts [22]. Therefore, to measure the resonance structures of neutron-induced reactions [23–26], neutrons with better monochromaticity are expected [27]. This can be realized using a monoenergetic neutron source with a higher energy resolution.

During the study of neutron–proton (n–p) reactions in inverse kinematics, the idea of designing high-resolution single-energy neutron beams in the keV to MeV energy range has been proposed. In this study, the inverse kinematics of collisions between thermal neutrons and high-energy protons was studied using the Monte Carlo method. A detailed Monte Carlo method that regards neutrons as the target particle is described in Sect. 2,wherein the acceleration of neutrons after collision with protons is simulated and the energy spectrum and direction information of outgoing neutrons are obtained. The simulation results are presented in Sect. 3.In Sect. 4,a possible application that may help to yield high-resolution singleenergy neutron beams in the keV to MeV energy range is proposed. The conceptual system design of a monoenergetic neutron source is presented, and some basic parameters are evaluated. Parameter estimation indicates that the designed system performs well in obtaining monoenergetic neutrons in a wide energy range with a high energy resolution of up to the order of 0.1%.

2 Calculations

To simulate the physical process of collisions between thermal neutrons and high-energy proton beams, basic information about collisions, the key parameters of proton beams and thermal neutrons should be studied.The Monte Carlo method is then used to simulate the collision and obtain the physical information of the outgoing neutrons.

2.1 Reaction cross section

First, the sampling rule used in the Monte Carlo simulation was obtained from the cross-section library. The evaluated nuclear data file ENDF/B-VIII.0 stores the neutron reaction cross-section information. From the ACE format [28] database, the reaction type and angular distribution [29] of the reaction can be determined. It can be determined from the cross-section data of neutrons and1H that the type of n–p reaction is mainly elastic scattering.The inelastic reaction type cross section is 2 ～5 orders of magnitude smaller than the elastic scattering cross section,so that the inelastic reaction can be ignored when simulating the reaction between1H and neutrons.

2.2 Methods

In this study, the Monte Carlo method was used to simulate the physical process. Usually, the Monte Carlo simulation of neutron transport tracks the state of incident neutrons by recognizing the neutron as the incident particle.The target nucleus is taken at rest.In most cases where the target has heavy nuclei,this assumption does not cause excessive errors. However, the mass of protons is comparable to that of neutrons, and the thermal motion of neutrons as target particles should also be considered in the neutron transport simulation. In this simulation, thermal neutrons were the target, while monoenergetic protons were defined as incident particles.It is known that physical laws maintain consistency in different frames of reference.Therefore, it is reasonable to develop a Monte Carlo program to simulate the p–n collision process in the center-ofmass system [30].

By referring to the sampling method in the MCNP, the simulation flowchart is designed as shown in Fig. 1.

First, the simulation program initializes the energy and velocity directions of the protons and neutrons. Protons were set to be monoenergetic and unidirectional. Neutron energies, in terms of velocity, were sampled from the Maxwellian distribution [30]

The second step was to simulate the collisions between protons and neutrons. After sampling the initial neutron velocity, the elastic scattering cross section was recalculated for each n–p collision process using the relative energies Er of neutrons and protons. The relative velocity was calculated using

where vrel is the n–p relative velocity, vp is the proton velocity, vn is the neutron velocity sampled from the

Fig.1 Monte Carlo simulation flowchart of n–p collisions in inverse kinematics

Fig. 2 Sampling of neutron velocity direction

Maxwellian distribution, and μt is the cosine of the angle between the direction of the incident proton and the direction of the collided neutron.Then,the cross section of the n–p reaction, including elastic scattering and inelastic scattering, was recalculated by interpolation in the ENDF/B1H cross-section library. After acquiring the cross section, the reaction type was determined by sampling. The elastic scattering type was sampled with a probability of Pel calculated using

where σel is the elastic scattering cross section and σin is the inelastic scattering cross section.

According to two-body kinematics,the outgoing neutron energy is a function of the scattering angle. The neutron scattering angle below was sampled in a neutron-at-rest system by interpolating the relative energy Er in the crosssection library of the angular distribution of1H.In the ACE format library, the angular distributions are represented by a tabulation of the probability density functions (PDFs),providing a table of cosines μi，k, probability density functions pi，k, and cumulative density functions ci，k(where k represents the kth cosine bin)for each incident energy grid Ei. The interpolation of the PDF needs to identify the correct position of Er, where Ei＜Er＜Ei+1. The interpolation fraction was defined as r =（Er-Ei）/（Ei+1-Ei）.In the sampling, Eiwas tabulated with a probability of 1-r and Ei+1was tabulated with a probability of r. A random number ξ1was then produced on the unit interval[0,1) to sample cosine bin k from the cumulative density function.The cosine of the scattering angle μ was sampled by linear interpolation in the PDF using [30]

The azimuth angle φ was uniformly sampled in the range of [0,2π). As all the samplings of the neutron exit parameters above are conducted in a neutron-at-rest system, the direction of neutron emission needs to be transformed into a laboratory system. This was performed using [32]

where Ein is the incident proton energy and μc is the cosine of the angle between the proton incident direction and the neutron exiting direction in the center-of-mass system.

3 Results

In the simulation, the energy of the protons was initialized to the same value.We take 200 keV as an example to demonstrate the simulation results and laws. The statistical graph of the existing neutron velocity vectors after n–p elastic scattering is displayed in Fig. 3.

Fig. 3 Exiting neutron velocity vector statistical graph

Fig. 4 Relationship between outgoing neutron energy En and cos θL(cosine of the scattering angle in the laboratory frame of reference)

It is easy to observe a clear relationship between the outgoing neutron energy and the exiting angle θLin Fig. 4.The outgoing neutron energy is at a maximum at θL=0°.The curve of the neutron energy versus outgoing direction fits the relation En =Ep·（cos θL）2. This implies that a monoenergetic neutron beam can be obtained by screening θL, the outgoing angle of neutrons in the laboratory frame of reference. When the outgoing angle of the neutron is fixed, the neutron energy varies linearly with the proton energy; for example, when θL=0°, En =Ep.

4 Discussion

4.1 Application design

In the elastic collision simulation, a simple relationship was derived between neutrons and protons. The results above suggest that a monoenergetic neutron beam can be easily obtained by controlling the energy of the incident proton beam and the outgoing angle of the neutron. With the development of neutron sources and monoenergetic proton accelerators, this may be a good method to obtain monoenergetic neutron beams. It is universally acknowledged that a qualified single-energy neutron source should also have a high yield.Therefore,the scattering angle with the highest probability of emission was the optimum output angle. The cross-section data were derived from the evaluated nuclear data file, ENDF/B-VIII.0, which stores the neutron reaction cross-section information. We can read out the data in ACE format [28] and obtain the angular distribution of the elastic scattering differential cross section [29] between the neutron and1H from the database.The angular distribution of the n–p elastic scattering under different incident energies is depicted in Fig. 5. It can be seen in Fig. 5a that the most probable scattering angle of the secondary neutron is θL=0°in all energy ranges.Figure 5b shows an example of the cross-sectional angular distribution when the incident energy is 200 keV.

Fig. 5 (a) Angular distribution of n–p elastic scattering with different incident proton energies. (b) Angular distribution of n–p elastic scattering at 200 keV. (c) n–p elastic scattering cross section with different incident neutron energies at 294 K

The neutron yield reaches its peak for elastic center-tocenter collisions between protons and neutrons. Meanwhile,the energy of the outgoing neutron equals the energy of the incident proton. Therefore, an angle of 0°was chosen to be the best outgoing angle. The relationship between the total n–p elastic cross section and energy is shown in Fig. 5c. Based on the law of elastic scattering, a system to obtain a monoenergetic neutron source can be designed, as shown in Fig. 6.

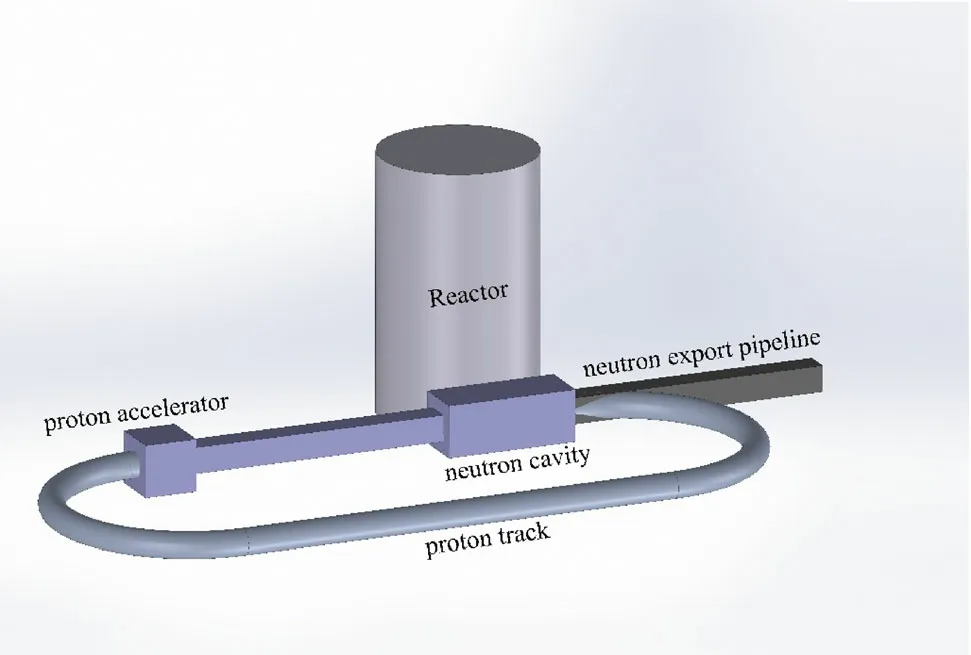
Fig. 6 (Color online) System design of the monoenergetic neutron source

The design mainly consists of three parts:a neutron cell,a proton track and a neutron export pipe. The neutron cell is a vacuum space inside a neutron moderator measuring 20 cm × 20 cm × 50 cm in width, height and length,respectively. Based on the neutron source reactor, the neutrons to be accelerated are fully slowed by the moderator. Subsequently, neutrons enter the cell, waiting to collide. The primary energy of the neutrons is considered to be much lower than that of the protons, so that the neutron primary energy can be ignored.Protons accelerated to specific energies by the proton accelerator pass energy to neutrons through elastic scattering. Protons that do not collide with neutrons are separated from monoenergetic neutron beams by a magnetic field.If the protons are to be recycled,the protons can be oriented back by the design of the proton track. The neutron export pipe, which only allows neutrons with a scattering angle of 0°to pass through,is a neutron absorber with many vacuum channels distributed in it.Single-energy neutron beams were derived from the output side of the pipe.The output neutron energy can be adjusted by controlling proton energy.

4.2 Parameter analysis

4.2.1 Energy resolution

To confirm the feasibility of the conceptual design, the Monte Carlo method was applied to simulate and calculate its important parameters. Simulation of p–n collisions was conducted with an incident proton energy of 200 keV. In the previous simulation, protons were monoenergetic, and neutron energy was sampled from a Maxwellian distribution. In fact, neutrons coming from the reactor are moderated before entering the neutron cell; their energy spectrum does not exactly match a Maxwellian distribution, and the neutron velocity direction in the cell is not isotropic. To obtain a better simulation of the physical process, the initialization of neutrons was optimized. For the sampling of neutrons, a simple reactor-based neutron source model was built using UO2as fuel, H2O, and a graphite layer as the moderator. A cross-sectional view of the model is depicted in Fig. 7. The model simulates the process of fission neutrons reaching the neutron cell after moderation by the water and graphite layers. The energy spectrum and direction of neutrons that reach the neutron cell were determined and used to initialize the neutron parameters in the collision simulation program.

Collisions between protons and neutrons were simulated with protons sampled from a Gaussian distribution and neutrons sampled from a reactor-based moderated neutron model. The relationship between the neutron energy and the cosine of the neutron scattering angle after collision is shown in Fig. 8.

Some data points deviate from the fitting curve because of the energy dispersion of protons and neutrons. Most points in the figure still conform to the law of elastic scattering between protons and stationary neutrons,implying that a monoenergetic neutron beam can be obtained by screening the 0°scattering angle. Therefore,the neutron screening process was simulated to obtain a single-energy neutron beam. By distributing vacuum channels inside the neutron absorber, only the neutrons emitted at a 0°scattering angle can be exported through the export pipe,and those emitted at other angles are absorbed by the material such that a monoenergetic neutron beam with an energy equal to the incident proton energy Ep can be exported.The neutron pipe was designed with 4 cm by 4 cm square vacuum channels with sides distributed inside a neutron absorber with a length of 100 cm. Boron and its compound boron carbide (B4C) [33] are suitable neutron absorber materials for neutron export pipelines. In engineering practice, boron-doped polyethylene with a density of 1.3 g·cm-3and a boron carbide content of 30% [34] is used as the absorbing material. A simulation model of the neutron export pipeline is shown in Fig. 9.

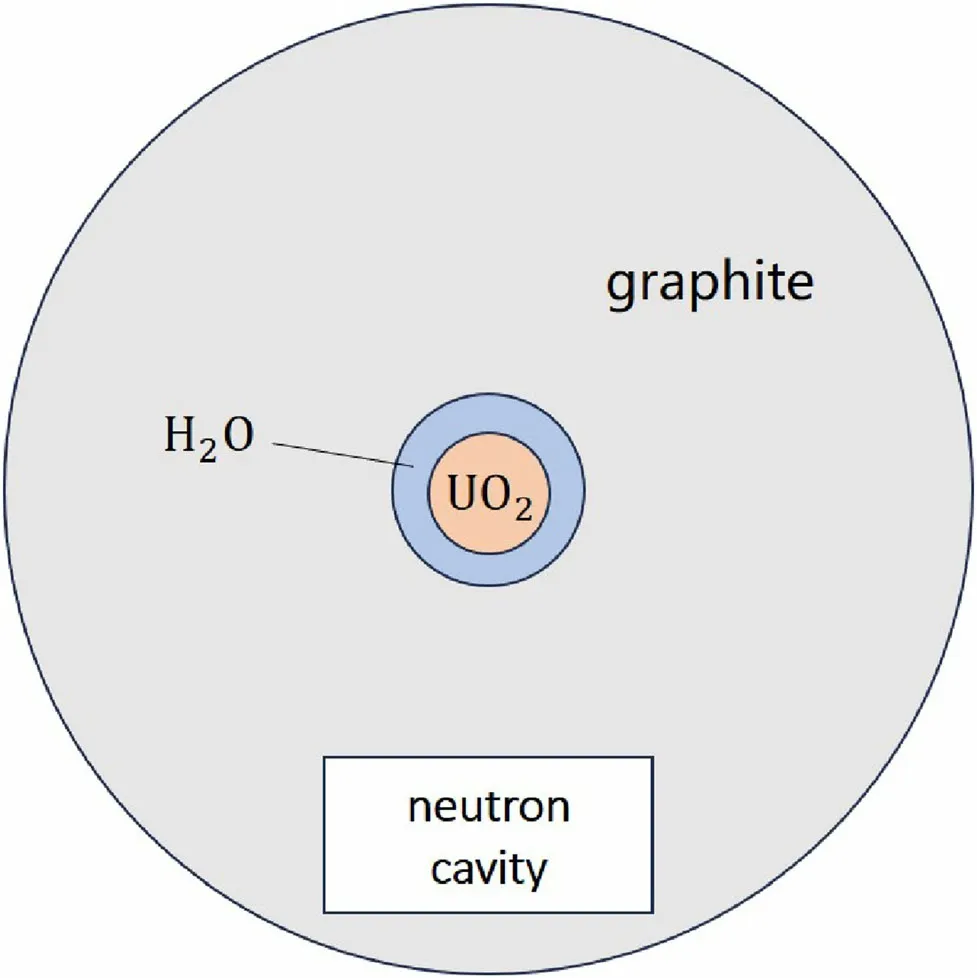
Fig. 7 Neutron source reactor model

Fig. 8 Fitting of exiting energy and scattering angle

In the simulation of neutron screening, neutrons are initialized with the energy spectrum and direction derived from the collision simulation program in the previous step.The program then tracks the neutron transport process in the neutron export pipe and tallies the neutrons that can pass through to obtain the output neutron energy spectrum after screening in Fig. 10.

The simulated energy resolution of the designed monoenergetic neutron source after optimization was calculated as follows:

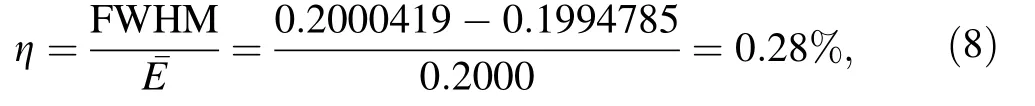
where FWHM is the full width half maximum energy and¯E is the average energy. This result demonstrates that the single-energy neutron beam produced by the design has excellent monochromaticity and satisfactory directionality.

Fig. 9 Schematic of the neutron export pipeline

Fig. 10 Neutron energy spectrum (left) and the energy peak (right)after screening of reactor-based neutrons

For different target energies Eaim, the designed system is supposed to produce a monoenergetic neutron beam adhering to the relationship Ep =Eaim =En. However,different target energies may influence the energy resolution. The design is based on the hypothesis that the primary energy of neutrons is so low that it is negligible compared to the target energy Eaim. However, the initial velocity of the neutron before collision will lead to divergence of the neutron energy. Owing to the broadening of the exiting angle caused by the geometry of the neutron export pipeline (as shown in Fig. 9), there is a broadening of the energy peak.According to the design of the neutron export pipeline, the length of the pipeline is 100 cm, and the channel cross section is a square of 4 cm by 4 cm, and the average broadening of the exiting angle Δ¯θ can be calculated by using

Next, consider the thermal motion of neutrons and the energy dispersion and transverse distribution before collision.It is assumed that the primary energy of the neutron is E0,the angle between the directions of neutron and proton movement in the laboratory frame of reference is denoted by α, and the relationship among the incident proton velocity vp,neutron initial velocity v0,and relative velocity of neutrons and protons,vrel, based on the cosine theorem can be represented as follows:

Fig. 11 Relationship among vp，v0, and vrel

Obviously, when the target energy Eaim =Ep is low, for instance, when the target energy is on the order of eV, the neutron primary energy E0is close to the proton energy Ep,and the error caused by the neutron primary velocity becomes obvious. The Monte Carlo simulation of the collision and screening process was then repeated in different energy ranges to obtain the energy spectrum and resolution of the outgoing neutron beam. A comparison between the simulated and theoretical energy resolutions is given in Table 1 and shown in Fig. 12.

A comparison between the theoretical and simulated energy resolutions is presented in Fig. 12.

As depicted in Fig. 12,in the wide energy range of keV and above, the energy resolution of the obtained monoenergetic neutrons is high, basically ～0.3%. However,owing to the hypothesis of stationary neutrons, the system performs poorly in the eV energy region, with an energy resolution of ～0.5%, which is also a good result. For high-energy neutrons with energies of ≥1 MeV, the simulated energy resolution of the peak is high. The energy resolution results demonstrate that this design is a good application for p–n collisions.

4.2.2 Neutron intensity estimation

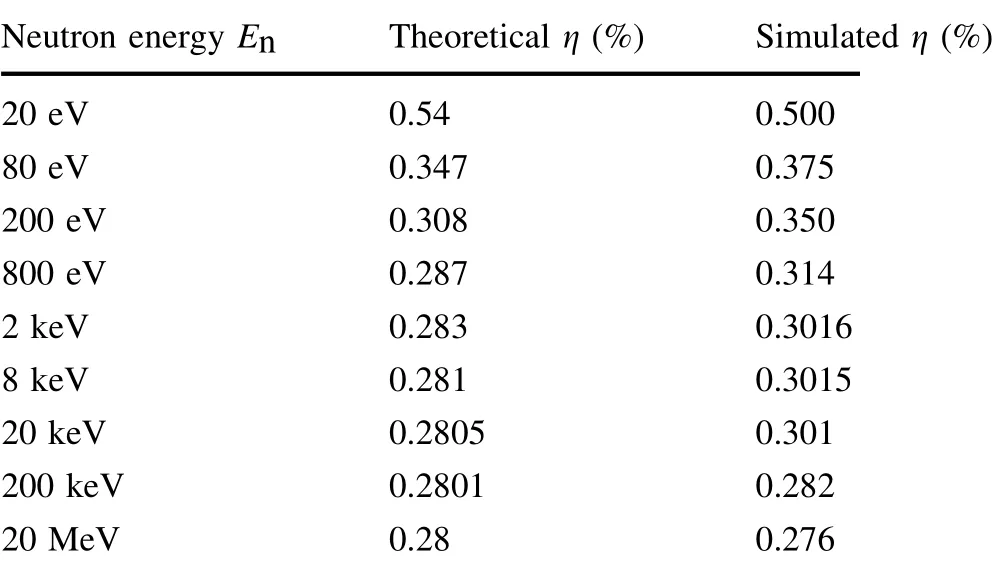
Table 1 Energy resolution of the theoretical calculation and simulation

Fig. 12 Comparison between simulated and theoretical system energy resolution

The estimated result for the source intensity is 500 n·s-1,which is not ideal as all the parameters were chosen under conservative estimation. This implies that the output neutron intensity can be improved through several methods,such as enlarging the volume of the neutron cell.A reactorbased neutron source with a higher neutron flux can also be used to increase the neutron intensity. When the proton energy is not very high,it is possible to increase the proton current on the proton accelerator. Such high-energy-resolution neutrons can be applied to scientific measurements that do not require neutron intensity to be very high [10].Neutrons with better monochromaticity [27] may help to improve the measurement of resonance structures of neutron-induced reactions [23–25] and evaluation of nuclear data [26]. The monoenergetic neutron beam design proposed based on inverse kinematics of n–p collisions in this study may help promote the acquisition of a better singleenergy neutron source.

4.3 Influence of proton dispersion

To obtain a better simulation of the system’s physical process, the energy dispersion and transverse distribution of the proton beam should be considered in the Monte Carlo simulation of p–n collisions. The typical momentum dispersion of proton accelerators is Δp/p=0.1% [37];therefore, the energy dispersion of the proton beam can be taken as ΔEp/Ep =2Δp/p=0.2%. In the simulation, the proton energy was sampled with a Gaussian distribution whose mean energy was taken as Ep and the standard deviation can be taken as σ=ΔEp/Ep =0.2%. The transverse velocity direction of the proton can be sampled uniformly in [0, 2π). Collisions between protons and neutrons with protons sampled from a Gaussian distribution and neutrons sampled from the reactor-based moderated neutron model was simulated.The relationship between the neutron energy and the cosine of the neutron scattering angle after collision has already been taken into consideration in the results shown in Fig. 8.Generally,the neutron exiting energy and cosine of the scattering angle are in accordance with the screening angle relation. Next, we conducted a further simulation of neutron-passing export pipelines and derived the monoenergetic neutron energy spectrum after the screening process. The simulation results are presented in Fig. 13.

In summary, after taking all these factors of proton energy dispersion and transverse distribution as well as the energy spectrum and flight direction of reactor-based neutrons into consideration, the designed system can still acquire an energy resolution up to a magnitude of 0.1%,which is a good result for monoenergetic neutron sources.

5 Conclusion

Fig.13 Neutron energy spectrum and the energy peak after screening by considering proton energy dispersion and the transverse distribution

In this study, Monte Carlo simulations were performed on n–p collisions in inverse kinematics by taking neutrons as target particles. It is necessary to use such a method when the behaviors of both neutrons and targets should be taken into account.This method was applied to simulate p–n collisions under a high-flux thermal neutron field. The relationship between neutron energy and exiting angle after thermal neutrons collided with high-energy protons was then analyzed. The results suggest that, when high-energy protons collide with thermal neutrons, the energy of outgoing neutrons corresponds to the scattering angle.Specifically, when θL=0°, the neutron energy equals the incident proton energy.

Based on these results, a conceptual design in which thermal neutrons collide with a proton beam of the target energy and the 0°scattering angle is chosen to obtain neutrons of the target energy was proposed. The goal was to provide inspiration for the acquisition of monoenergetic neutrons with higher energy resolution. The advantage of this design is that the output neutron beams have excellent directionality and monochromaticity with an energy resolution of up to 0.1%. However, the idea is merely a conceptual design. Its feasibility requires further study, and there is much improvement needed in neutron intensity and the implementation of the proton track design.

Author ContributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Bi-Lu Li. The first draft of the manuscript was written by Bi-Lu Li,and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.